1.3 三角函数的计算 课时作业(含答案) 2024-2025学年数学北师大版九年级下册
文档属性
| 名称 | 1.3 三角函数的计算 课时作业(含答案) 2024-2025学年数学北师大版九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 168.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-26 21:18:29 | ||
图片预览


文档简介
3 三角函数的计算
用科学计算器求锐角三角函数值
1.(2024东营期中)用科学计算器求sin 9°7'的值,按键顺序正确的是 ( )
A. SHIFT sin 9 7 =
B. sin 9 ° ' ″ 7 ° ' ″ =
C. SHIFT sin 9 ° ' ″ 7 =
D. ° ' ″ sin 9 SHIFT 7 =
2.如果3sin α=+1,则α= .(精确到0.1°)
3.在Rt△ABC中,∠C=90°,∠A=42°,BC=3,则AC的长为 .(用科学计算器计算,结果精确到0.01)
4.用计算器求下列各式的值(结果精确到0.000 1):
(1)sin 47°;
(2)sin 12°30';
(3)cos 25°18';
(4)tan 44°59'59″;
(5)sin 18°+cos 55°-tan 59°.
知三角函数值求角度
5.锐角A满足cos A=,利用计算器求∠A时,依次按键SHIFT cos ( 1 ÷ 2 ) =,∠A的度数为 .
6.在Rt△ABC中,∠C=90°,AC=8,AB=2,则∠A的大小为 .(精确到0.1°)
三角函数的实际应用
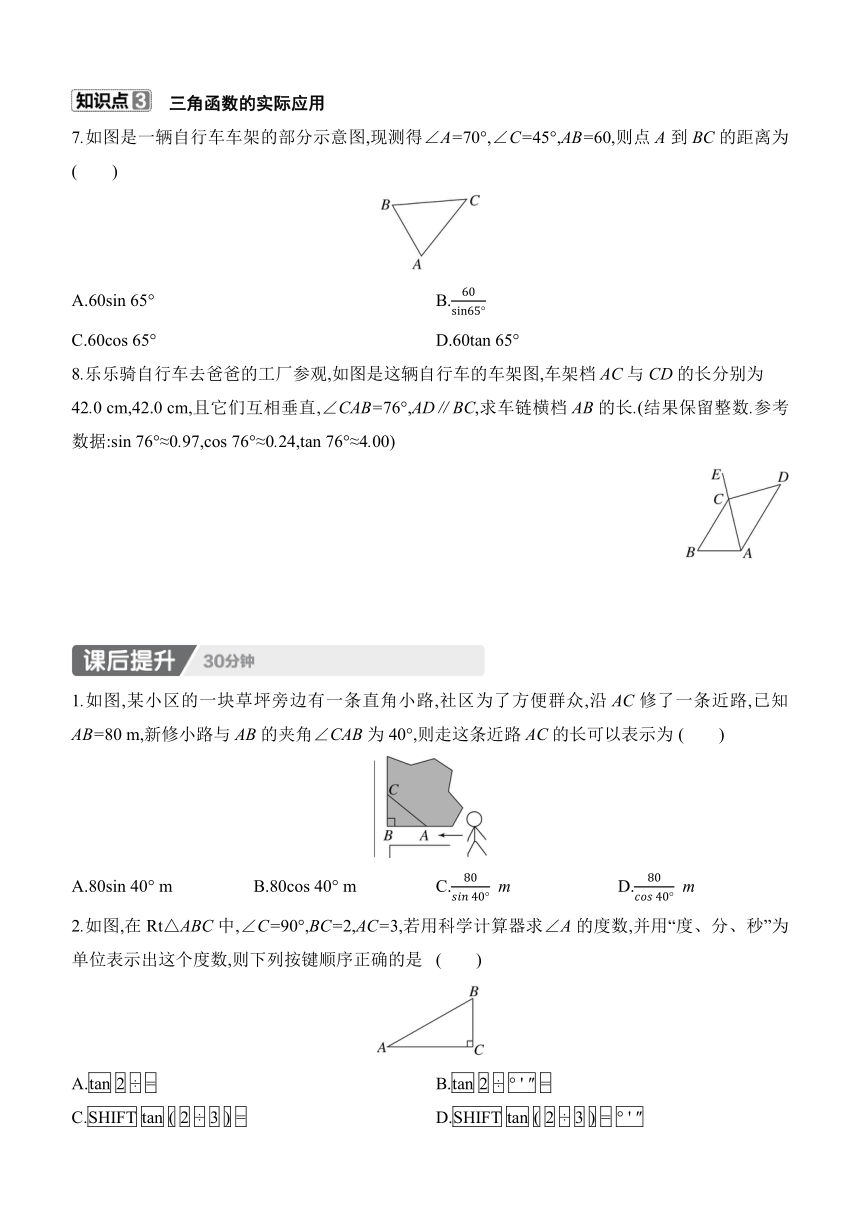
7.如图是一辆自行车车架的部分示意图,现测得∠A=70°,∠C=45°,AB=60,则点A到BC的距离为( )
A.60sin 65° B.
C.60cos 65° D.60tan 65°
8.乐乐骑自行车去爸爸的工厂参观,如图是这辆自行车的车架图,车架档AC与CD的长分别为
42.0 cm,42.0 cm,且它们互相垂直,∠CAB=76°,AD∥BC,求车链横档AB的长.(结果保留整数.参考数据:sin 76°≈0.97,cos 76°≈0.24,tan 76°≈4.00)
1.如图,某小区的一块草坪旁边有一条直角小路,社区为了方便群众,沿AC修了一条近路,已知AB=80 m,新修小路与AB的夹角∠CAB为40°,则走这条近路AC的长可以表示为 ( )
A.80sin 40° m B.80cos 40° m C. m D. m
2.如图,在Rt△ABC中,∠C=90°,BC=2,AC=3,若用科学计算器求∠A的度数,并用“度、分、秒”为单位表示出这个度数,则下列按键顺序正确的是 ( )
A.tan 2 ÷ = B.tan 2 ÷ ° ' ″ =
C.SHIFT tan ( 2 ÷ 3 ) = D.SHIFT tan ( 2 ÷ 3 ) = ° ' ″
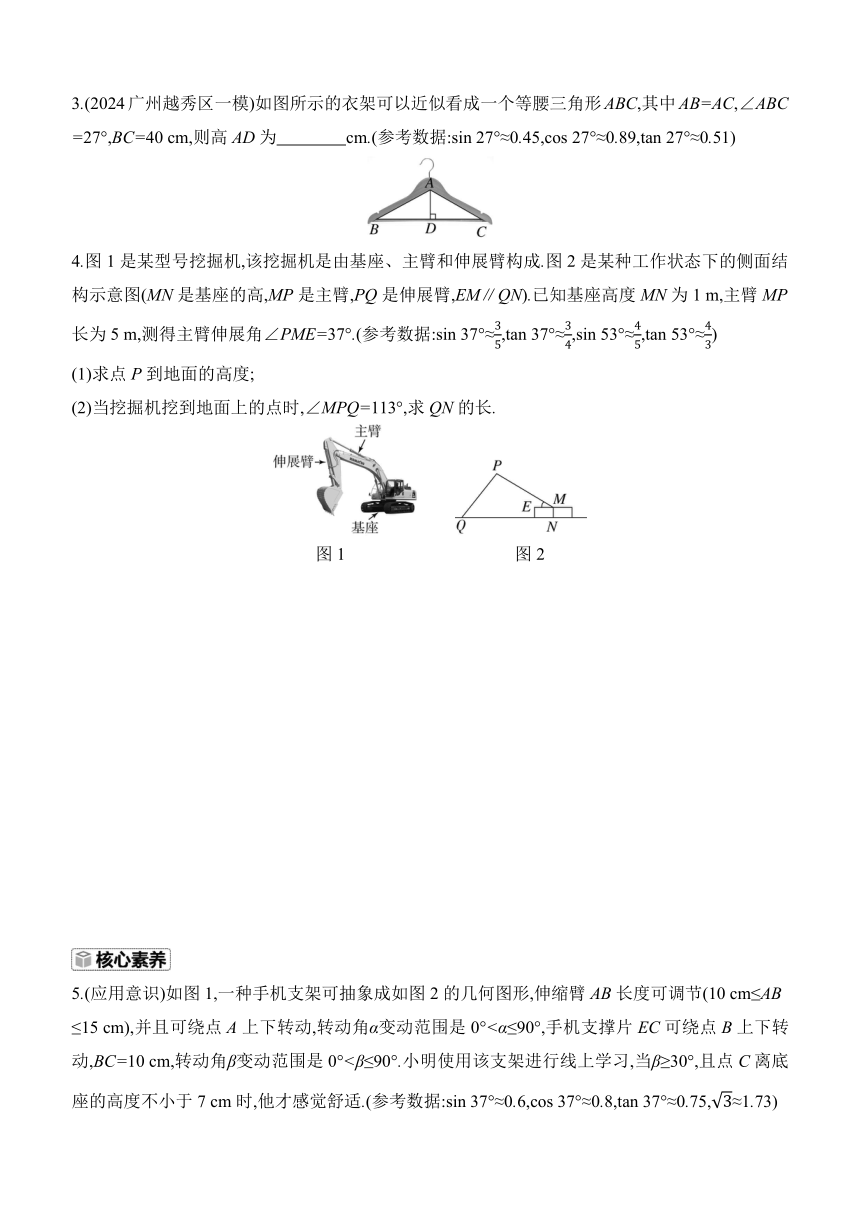
3.(2024广州越秀区一模)如图所示的衣架可以近似看成一个等腰三角形ABC,其中AB=AC,∠ABC
=27°,BC=40 cm,则高AD为 cm.(参考数据:sin 27°≈0.45,cos 27°≈0.89,tan 27°≈0.51)
4.图1是某型号挖掘机,该挖掘机是由基座、主臂和伸展臂构成.图2是某种工作状态下的侧面结构示意图(MN是基座的高,MP是主臂,PQ是伸展臂,EM∥QN).已知基座高度MN为1 m,主臂MP长为5 m,测得主臂伸展角∠PME=37°.(参考数据:sin 37°≈,tan 37°≈,sin 53°≈,tan 53°≈)
(1)求点P到地面的高度;
(2)当挖掘机挖到地面上的点时,∠MPQ=113°,求QN的长.
图1 图2
5.(应用意识)如图1,一种手机支架可抽象成如图2的几何图形,伸缩臂AB长度可调节(10 cm≤AB
≤15 cm),并且可绕点A上下转动,转动角α变动范围是0°<α≤90°,手机支撑片EC可绕点B上下转动,BC=10 cm,转动角β变动范围是0°<β≤90°.小明使用该支架进行线上学习,当β≥30°,且点C离底座的高度不小于7 cm时,他才感觉舒适.(参考数据:sin 37°≈0.6,cos 37°≈0.8,tan 37°≈0.75,≈1.73)
(1)如图2,当α=90°,β=37°,AB=12 cm时,求托片底部点C离底座的高度,并判断是否符合小明使用的舒适要求;
(2)如图3,当α=60°,β=90°的情况下,AB要伸缩到多少厘米时才能满足点C离底座的最低高度舒适要求 (精确到1 cm)
图1 图2 图3
【详解答案】
课堂达标
1.B 解析:根据科学计算器的按键顺序可知,正确的按键顺序是B选项.
故选B.
2.65.6° 解析:∵3sin α=+1,
∴sin α=,
解得α≈65.6°.
3.8.16 解析:∵tan 42°≈0.900 4,
∴=0.900 4,
∴AC≈8.16.
4.解:根据题意用计算器求出:
(1)sin 47°≈0.731 4.
(2)sin 12°30'≈0.216 4.
(3)cos 25°18'≈0.904 1.
(4)tan 44°59'59″≈1.000 0.
(5)sin 18°+cos 55°-tan 59°≈-0.781 7.
5.60° 解析:依次按键SHIFT cos ( 1 ÷ 2 ) =,显示的是∠A的度数为60°.
6.23.4° 解析:在Rt△ABC中,∠C=90°,AC=8,AB=2,
∵cos A=≈0.918,
∴∠A的大小为23.4°.
7.A 解析:如图,过点A作AD⊥BC,垂足为D.
∵∠BAC=70°,∠C=45°,
∴∠B=180°-∠BAC-∠C=65°.
在Rt△ABD中,AB=60,
∴AD=AB·sin 65°=60sin 65°,
∴点A到BC的距离为60sin 65°,
故选A.
8.解:如图,过点B作BH⊥AC,垂足为H,
则tan∠BAH=.
∵AC=42.0 cm,CD=42.0 cm,
AC⊥CD,
∴∠CAD=∠ADC=45°.
∵AD∥BC,
∴∠ACB=∠CAD=45°,
∴tan ∠ACB=1.
设BH=CH=x cm,AH=(42.0-x)cm,
则tan 76°=≈4.00,
解得x=33.6,
经检验,x=33.6是所列分式方程的解.
∴BH=33.6 cm,AH=8.4 cm,
∴AB=≈35(cm).
答:车链横档AB的长为35 cm.
课后提升
1.D 解析:在Rt△ABC中,
∵AB=80 m,∠CAB=40°,
∴=cos 40°,
∴AC=(m),
故选D.
2.D 解析:由tan A=,得
tan A=.
再根据科学计算器的按键顺序可知,正确的按键顺序是D选项.
故选D.
3.10.2 解析:∵AB=AC,AD⊥BC,BC=40 cm,
∴BD=BC=20 cm.
在Rt△ABD中,∠ABC=27°,
∴AD=BD·tan 27°≈20×0.51=10.2(cm),
∴高AD约为10.2 cm.
4.解:(1)如图,过点P作PG⊥QN,垂足为G,延长ME交PG于点F.
由题意,得MF⊥PG,MF=GN,FG=MN=1 m.
在Rt△PFM中,∠PMF=37°,PM=5 m,
∴PF=PM·sin 37°≈5×=3(m),
∴PG=PF+FG=3+1=4(m),
∴点P到地面的高度约为4 m.
(2)∵∠PMF=37°,∠PFM=90°,
∴∠MPF=53°.
∵∠MPQ=113°,
∴∠QPG=113°-53°=60°.
∵PG=4 m,
∴QG=PG=×4=4(m).
∵PM=5 m,PF=3 m,
∴FM==4(m),
∴QN=QG+NG=(4+4)m.
5.解:(1)过点C作CF⊥AB于点F,如图1.
图1
在Rt△BCF中,
BF=BC·cos β=10×cos 37°≈8(cm),
∴AF=AB-BF=12-8=4(cm).
∵4<7,
∴托片底部点C离底座的高度为4 cm,不符合小明使用的舒适要求.
(2)过点B作BH⊥AD于点H,过点C作CM⊥BH于点M,如图2.
图2
在Rt△ABH中,α=60°,
∴∠ABH=90°-60°=30°,
∴∠CBM=90°-30°=60°.
在Rt△BCM中,
BM=BC·cos 60°=10×=5(cm).
∵要满足点C离底座的最低舒适要求,
∴MH=7 cm,
则BH=BM+MH=12 cm,
∴AB==8≈14(cm),
∴至少要将AB伸缩至14 cm时才能符合小明的舒适要求.
用科学计算器求锐角三角函数值
1.(2024东营期中)用科学计算器求sin 9°7'的值,按键顺序正确的是 ( )
A. SHIFT sin 9 7 =
B. sin 9 ° ' ″ 7 ° ' ″ =
C. SHIFT sin 9 ° ' ″ 7 =
D. ° ' ″ sin 9 SHIFT 7 =
2.如果3sin α=+1,则α= .(精确到0.1°)
3.在Rt△ABC中,∠C=90°,∠A=42°,BC=3,则AC的长为 .(用科学计算器计算,结果精确到0.01)
4.用计算器求下列各式的值(结果精确到0.000 1):
(1)sin 47°;
(2)sin 12°30';
(3)cos 25°18';
(4)tan 44°59'59″;
(5)sin 18°+cos 55°-tan 59°.
知三角函数值求角度
5.锐角A满足cos A=,利用计算器求∠A时,依次按键SHIFT cos ( 1 ÷ 2 ) =,∠A的度数为 .
6.在Rt△ABC中,∠C=90°,AC=8,AB=2,则∠A的大小为 .(精确到0.1°)
三角函数的实际应用
7.如图是一辆自行车车架的部分示意图,现测得∠A=70°,∠C=45°,AB=60,则点A到BC的距离为( )
A.60sin 65° B.
C.60cos 65° D.60tan 65°
8.乐乐骑自行车去爸爸的工厂参观,如图是这辆自行车的车架图,车架档AC与CD的长分别为
42.0 cm,42.0 cm,且它们互相垂直,∠CAB=76°,AD∥BC,求车链横档AB的长.(结果保留整数.参考数据:sin 76°≈0.97,cos 76°≈0.24,tan 76°≈4.00)
1.如图,某小区的一块草坪旁边有一条直角小路,社区为了方便群众,沿AC修了一条近路,已知AB=80 m,新修小路与AB的夹角∠CAB为40°,则走这条近路AC的长可以表示为 ( )
A.80sin 40° m B.80cos 40° m C. m D. m
2.如图,在Rt△ABC中,∠C=90°,BC=2,AC=3,若用科学计算器求∠A的度数,并用“度、分、秒”为单位表示出这个度数,则下列按键顺序正确的是 ( )
A.tan 2 ÷ = B.tan 2 ÷ ° ' ″ =
C.SHIFT tan ( 2 ÷ 3 ) = D.SHIFT tan ( 2 ÷ 3 ) = ° ' ″
3.(2024广州越秀区一模)如图所示的衣架可以近似看成一个等腰三角形ABC,其中AB=AC,∠ABC
=27°,BC=40 cm,则高AD为 cm.(参考数据:sin 27°≈0.45,cos 27°≈0.89,tan 27°≈0.51)
4.图1是某型号挖掘机,该挖掘机是由基座、主臂和伸展臂构成.图2是某种工作状态下的侧面结构示意图(MN是基座的高,MP是主臂,PQ是伸展臂,EM∥QN).已知基座高度MN为1 m,主臂MP长为5 m,测得主臂伸展角∠PME=37°.(参考数据:sin 37°≈,tan 37°≈,sin 53°≈,tan 53°≈)
(1)求点P到地面的高度;
(2)当挖掘机挖到地面上的点时,∠MPQ=113°,求QN的长.
图1 图2
5.(应用意识)如图1,一种手机支架可抽象成如图2的几何图形,伸缩臂AB长度可调节(10 cm≤AB
≤15 cm),并且可绕点A上下转动,转动角α变动范围是0°<α≤90°,手机支撑片EC可绕点B上下转动,BC=10 cm,转动角β变动范围是0°<β≤90°.小明使用该支架进行线上学习,当β≥30°,且点C离底座的高度不小于7 cm时,他才感觉舒适.(参考数据:sin 37°≈0.6,cos 37°≈0.8,tan 37°≈0.75,≈1.73)
(1)如图2,当α=90°,β=37°,AB=12 cm时,求托片底部点C离底座的高度,并判断是否符合小明使用的舒适要求;
(2)如图3,当α=60°,β=90°的情况下,AB要伸缩到多少厘米时才能满足点C离底座的最低高度舒适要求 (精确到1 cm)
图1 图2 图3
【详解答案】
课堂达标
1.B 解析:根据科学计算器的按键顺序可知,正确的按键顺序是B选项.
故选B.
2.65.6° 解析:∵3sin α=+1,
∴sin α=,
解得α≈65.6°.
3.8.16 解析:∵tan 42°≈0.900 4,
∴=0.900 4,
∴AC≈8.16.
4.解:根据题意用计算器求出:
(1)sin 47°≈0.731 4.
(2)sin 12°30'≈0.216 4.
(3)cos 25°18'≈0.904 1.
(4)tan 44°59'59″≈1.000 0.
(5)sin 18°+cos 55°-tan 59°≈-0.781 7.
5.60° 解析:依次按键SHIFT cos ( 1 ÷ 2 ) =,显示的是∠A的度数为60°.
6.23.4° 解析:在Rt△ABC中,∠C=90°,AC=8,AB=2,
∵cos A=≈0.918,
∴∠A的大小为23.4°.
7.A 解析:如图,过点A作AD⊥BC,垂足为D.
∵∠BAC=70°,∠C=45°,
∴∠B=180°-∠BAC-∠C=65°.
在Rt△ABD中,AB=60,
∴AD=AB·sin 65°=60sin 65°,
∴点A到BC的距离为60sin 65°,
故选A.
8.解:如图,过点B作BH⊥AC,垂足为H,
则tan∠BAH=.
∵AC=42.0 cm,CD=42.0 cm,
AC⊥CD,
∴∠CAD=∠ADC=45°.
∵AD∥BC,
∴∠ACB=∠CAD=45°,
∴tan ∠ACB=1.
设BH=CH=x cm,AH=(42.0-x)cm,
则tan 76°=≈4.00,
解得x=33.6,
经检验,x=33.6是所列分式方程的解.
∴BH=33.6 cm,AH=8.4 cm,
∴AB=≈35(cm).
答:车链横档AB的长为35 cm.
课后提升
1.D 解析:在Rt△ABC中,
∵AB=80 m,∠CAB=40°,
∴=cos 40°,
∴AC=(m),
故选D.
2.D 解析:由tan A=,得
tan A=.
再根据科学计算器的按键顺序可知,正确的按键顺序是D选项.
故选D.
3.10.2 解析:∵AB=AC,AD⊥BC,BC=40 cm,
∴BD=BC=20 cm.
在Rt△ABD中,∠ABC=27°,
∴AD=BD·tan 27°≈20×0.51=10.2(cm),
∴高AD约为10.2 cm.
4.解:(1)如图,过点P作PG⊥QN,垂足为G,延长ME交PG于点F.
由题意,得MF⊥PG,MF=GN,FG=MN=1 m.
在Rt△PFM中,∠PMF=37°,PM=5 m,
∴PF=PM·sin 37°≈5×=3(m),
∴PG=PF+FG=3+1=4(m),
∴点P到地面的高度约为4 m.
(2)∵∠PMF=37°,∠PFM=90°,
∴∠MPF=53°.
∵∠MPQ=113°,
∴∠QPG=113°-53°=60°.
∵PG=4 m,
∴QG=PG=×4=4(m).
∵PM=5 m,PF=3 m,
∴FM==4(m),
∴QN=QG+NG=(4+4)m.
5.解:(1)过点C作CF⊥AB于点F,如图1.
图1
在Rt△BCF中,
BF=BC·cos β=10×cos 37°≈8(cm),
∴AF=AB-BF=12-8=4(cm).
∵4<7,
∴托片底部点C离底座的高度为4 cm,不符合小明使用的舒适要求.
(2)过点B作BH⊥AD于点H,过点C作CM⊥BH于点M,如图2.
图2
在Rt△ABH中,α=60°,
∴∠ABH=90°-60°=30°,
∴∠CBM=90°-30°=60°.
在Rt△BCM中,
BM=BC·cos 60°=10×=5(cm).
∵要满足点C离底座的最低舒适要求,
∴MH=7 cm,
则BH=BM+MH=12 cm,
∴AB==8≈14(cm),
∴至少要将AB伸缩至14 cm时才能符合小明的舒适要求.
