1.4 解直角三角形 课时作业(含答案) 2024-2025学年数学北师大版九年级下册
文档属性
| 名称 | 1.4 解直角三角形 课时作业(含答案) 2024-2025学年数学北师大版九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 154.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-26 21:18:05 | ||
图片预览




文档简介
4 解直角三角形
已知两边解直角三角形
1.(2024池州青阳县期末)如图,在△ABC中,∠ACB=90°,AC=4,BC=3,CD是△ABC的高,则
tan∠BCD的值是 ( )
A. B. C. D.
2.如图,在平面直角坐标系xOy中,已知点A(4,3),直线OA与x轴正半轴的夹角为α,那么sin α的值是 ( )
A. B. C. D.
3.(2024淄博张店区期末)在Rt△ABC中,∠C=90°,AC=,AB=2.解这个直角三角形.
已知一边及一锐角解直角三角形
4.如图,在Rt△ABC中,斜边AB的长为m,∠A=35°,则直角边BC的长是 ( )
A.msin 35° B.mcos 35° C. D.
5.已知Rt△ABC中,∠C=90°,∠B=60°,AB=6,解这个直角三角形.
已知一边及一锐角三角函数值解直角三角形
6.在Rt△ABC中,∠C=90°,BC=3,sin A=,则tan A= ( )
A. B. C. D.
7.在△ABC中,∠C=90°,AB=13,tan A=,则BC的长为 .
8.如图,在Rt△ABC中,∠C=90°,tan A=,BC=6,求AC的长和sin A的值.
9.如图,在矩形ABCD中,DE⊥AC于点E,设∠ADE=α,且sin α=,AB=4,求AD的长.
1.(2024衡阳期末)在Rt△ABC中,∠C=90°,若AB=5,cos B=,则AC等于 ( )
A. B.3 C.4 D.5
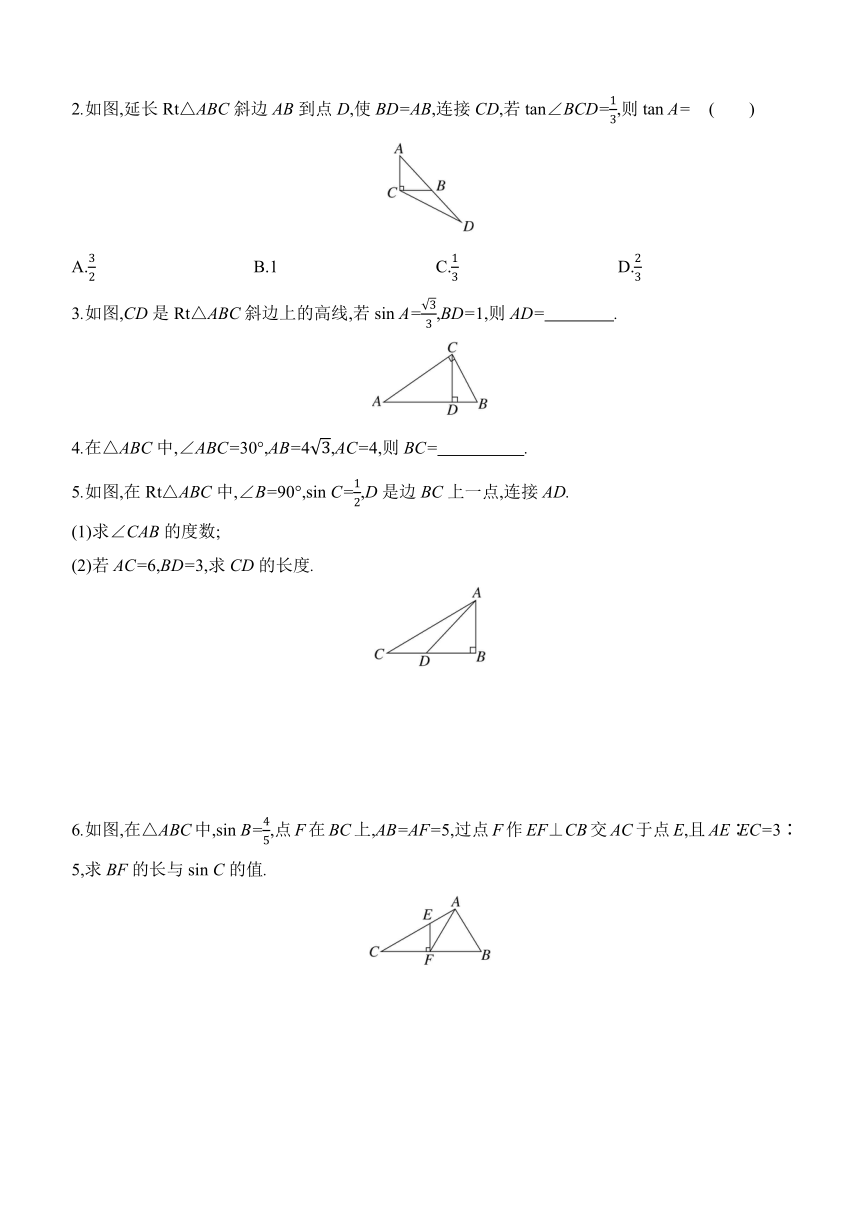
2.如图,延长Rt△ABC斜边AB到点D,使BD=AB,连接CD,若tan∠BCD=,则tan A= ( )
A. B.1 C. D.
3.如图,CD是Rt△ABC斜边上的高线,若sin A=,BD=1,则AD= .
4.在△ABC中,∠ABC=30°,AB=4,AC=4,则BC= .
5.如图,在Rt△ABC中,∠B=90°,sin C=,D是边BC上一点,连接AD.
(1)求∠CAB的度数;
(2)若AC=6,BD=3,求CD的长度.
6.如图,在△ABC中,sin B=,点F在BC上,AB=AF=5,过点F作EF⊥CB交AC于点E,且AE∶EC=3∶5,求BF的长与sin C的值.
7.(推理能力)如图,在△ABC中,AB=AC,AD为BC边上的中线,点E为AD的中点,过点A作AF∥BC,交BE的延长线于点F,连接CF.
(1)求证:四边形ADCF为矩形;
(2)若BC=6,sin∠BAD=,求EF的长.
【详解答案】
课堂达标
1.B 解析:∵∠ACB=90°,
∴∠BCD+∠ACD=90°.
∵CD⊥AB,∴∠ADC=90°,
∴∠DCA+∠A=90°,
∴∠BCD=∠A.
在Rt△ABC中,tan A=,
∴tan ∠BCD=tan A=,
故选B.
2.A 解析:如图,过点A作x轴的垂线,垂足为B.
由点A的坐标为(4,3)可知,
OB=4,AB=3,
∴AO==5.
在Rt△AOB中,
sin α=.
故选A.
3.解:由题可知,在Rt△ABC中,∠C=90°,AC=,AB=2,
∴BC==
.
∵tan A==1,
∴∠A=45°,
∴∠B=90°-∠A=90°-45°=45°.
4.A 解析:在Rt△ABC中,sin A=,
∵AB=m,∠A=35°,
∴BC=msin 35°,
故选A.
5.解:在Rt△ABC中,∵∠C=90°,∠B=60°,AB=6,
∴∠A=90°-60°=30°,
∴BC=AB=3,
∴AC==3.
6.A 解析:在Rt△ABC中,∠C=90°,BC=3,sin A=,且sin A=,
∴AB==5,
∴AC==4,
∴tan A=,
故选A.
7.5 解析:在Rt△ABC中,∠C=90°,
tan A=,
∴设BC=5x,则AC=12x,
∴AB==13x.
∵AB=13,
∴13x=13,
解得x=1,
∴BC=5x=5.
8.解:∵在Rt△ABC中,∠C=90°,tan A=,BC=6,
∴,∴AC=8,
∴AB==10,
∴sin A=.
9.解:∵四边形ABCD为矩形,
∴AD=BC,∠BAD=90°.
∵DE⊥AC,
∴∠ADE+∠DAE=90°.
而∠BAC+∠DAE=90°,
∴∠BAC=∠ADE=α.
在Rt△ABC中,∵sin∠BAC=,
∴.
设BC=4x,则AC=5x,
∴AB=3x,
∴3x=4,解得x=,
∴BC=
∴AD=.
课后提升
1.B 解析:∵在Rt△ABC中,∠C=90°,
∴cos B=.
∵AB=5,
∴BC=4,
∴AC==3.
故选B.
2.A 解析:如图,过B作BE∥AC交CD于点E.
∵AC⊥BC,
∴BE⊥BC,∴∠CBE=90°.
∵AB=BD,
∴AC=2BE.
又∵tan∠BCD=,设BE=x,则AC=2x,BC=3x,
∴tan A=,
故选A.
3.2 解析:∵CD是Rt△ABC斜边上的高线,
∴∠CDA=90°,∴∠A+∠ACD=90°.
又∵∠ACB=90°,∴∠ACD+∠BCD=90°,
∴∠A=∠BCD.
∵sin A=,
∴sin ∠BCD=.
∵BD=1,
∴BC=,
∴CD=.
∵sin A=,
∴AC=.
∴AD==2.
4.8或4 解析:①当∠ACB为锐角时,如图1,过点A作AD⊥BC,垂足为D.
图1
在Rt△ABD中,∵∠ABC=30°,AB=4,
∴AD=AB=2,BD=cos 30°×AB=6.
在Rt△ADC中,DC==2,
∴BC=BD+DC=6+2=8.
②当∠ACB为钝角时,如图2,过点A作AD⊥BC,交BC的延长线于点D.
图2
在Rt△ABD中,∵∠ABC=30°,AB=4,
∴AD=AB=2,BD=cos 30°×AB=6,
在Rt△ADC中,DC==2,
∴BC=BD-DC=6-2=4.
综上所述,BC的长为8或4.
5.解:(1)在Rt△ABC中,
∵sin C=,
∴∠C=30°,
∴∠CAB=90°-30°=60°.
(2)在Rt△ABC中,∠C=30°,
cos C=,
即,
∴BC=3,
∴CD=BC-BD=3-3.
6.解:过点A作AD⊥CB,垂足为点D,如图,
∵sin B=,∴.
∵AB=5,∴AD=4,∴BD=3.
∵AB=AF,AD⊥CB,
∴BF=2BD=6.
∵EF⊥CB,AD⊥CB,
∴EF∥AD,
∴.
∵AE∶EC=3∶5,DF=BD=3,
∴CF=5,∴CD=8.
在Rt△ACD中,AC==4,
∴sin C=.
7.解:(1)证明:∵AD是BC边上的中线,
∴BD=CD.
∵点E是AD的中点,
∴AE=ED.
∵AF∥BC,
∴∠AFE=∠DBE,∠FAE=∠BDE.
在△AFE和△DBE中,
∴△AFE≌△DBE(AAS),
∴AF=BD,
∴AF=DC.
又∵AF∥BC,
∴四边形ADCF为平行四边形.
∵AB=AC,AD为BC边上的中线,
∴AD⊥BC,
∴∠ADC=90°,
∴四边形ADCF为矩形.
(2)∵BC=6,AD为BC边上的中线,
∴BD=BC=3.
∵在Rt△ABD中,sin∠BAD=,
∴AB==5,
∴AD==4.
又∵点E为AD的中点,
∴ED=AD=2,
∴在Rt△EBD中,BE=,
∴EF=BE=.
已知两边解直角三角形
1.(2024池州青阳县期末)如图,在△ABC中,∠ACB=90°,AC=4,BC=3,CD是△ABC的高,则
tan∠BCD的值是 ( )
A. B. C. D.
2.如图,在平面直角坐标系xOy中,已知点A(4,3),直线OA与x轴正半轴的夹角为α,那么sin α的值是 ( )
A. B. C. D.
3.(2024淄博张店区期末)在Rt△ABC中,∠C=90°,AC=,AB=2.解这个直角三角形.
已知一边及一锐角解直角三角形
4.如图,在Rt△ABC中,斜边AB的长为m,∠A=35°,则直角边BC的长是 ( )
A.msin 35° B.mcos 35° C. D.
5.已知Rt△ABC中,∠C=90°,∠B=60°,AB=6,解这个直角三角形.
已知一边及一锐角三角函数值解直角三角形
6.在Rt△ABC中,∠C=90°,BC=3,sin A=,则tan A= ( )
A. B. C. D.
7.在△ABC中,∠C=90°,AB=13,tan A=,则BC的长为 .
8.如图,在Rt△ABC中,∠C=90°,tan A=,BC=6,求AC的长和sin A的值.
9.如图,在矩形ABCD中,DE⊥AC于点E,设∠ADE=α,且sin α=,AB=4,求AD的长.
1.(2024衡阳期末)在Rt△ABC中,∠C=90°,若AB=5,cos B=,则AC等于 ( )
A. B.3 C.4 D.5
2.如图,延长Rt△ABC斜边AB到点D,使BD=AB,连接CD,若tan∠BCD=,则tan A= ( )
A. B.1 C. D.
3.如图,CD是Rt△ABC斜边上的高线,若sin A=,BD=1,则AD= .
4.在△ABC中,∠ABC=30°,AB=4,AC=4,则BC= .
5.如图,在Rt△ABC中,∠B=90°,sin C=,D是边BC上一点,连接AD.
(1)求∠CAB的度数;
(2)若AC=6,BD=3,求CD的长度.
6.如图,在△ABC中,sin B=,点F在BC上,AB=AF=5,过点F作EF⊥CB交AC于点E,且AE∶EC=3∶5,求BF的长与sin C的值.
7.(推理能力)如图,在△ABC中,AB=AC,AD为BC边上的中线,点E为AD的中点,过点A作AF∥BC,交BE的延长线于点F,连接CF.
(1)求证:四边形ADCF为矩形;
(2)若BC=6,sin∠BAD=,求EF的长.
【详解答案】
课堂达标
1.B 解析:∵∠ACB=90°,
∴∠BCD+∠ACD=90°.
∵CD⊥AB,∴∠ADC=90°,
∴∠DCA+∠A=90°,
∴∠BCD=∠A.
在Rt△ABC中,tan A=,
∴tan ∠BCD=tan A=,
故选B.
2.A 解析:如图,过点A作x轴的垂线,垂足为B.
由点A的坐标为(4,3)可知,
OB=4,AB=3,
∴AO==5.
在Rt△AOB中,
sin α=.
故选A.
3.解:由题可知,在Rt△ABC中,∠C=90°,AC=,AB=2,
∴BC==
.
∵tan A==1,
∴∠A=45°,
∴∠B=90°-∠A=90°-45°=45°.
4.A 解析:在Rt△ABC中,sin A=,
∵AB=m,∠A=35°,
∴BC=msin 35°,
故选A.
5.解:在Rt△ABC中,∵∠C=90°,∠B=60°,AB=6,
∴∠A=90°-60°=30°,
∴BC=AB=3,
∴AC==3.
6.A 解析:在Rt△ABC中,∠C=90°,BC=3,sin A=,且sin A=,
∴AB==5,
∴AC==4,
∴tan A=,
故选A.
7.5 解析:在Rt△ABC中,∠C=90°,
tan A=,
∴设BC=5x,则AC=12x,
∴AB==13x.
∵AB=13,
∴13x=13,
解得x=1,
∴BC=5x=5.
8.解:∵在Rt△ABC中,∠C=90°,tan A=,BC=6,
∴,∴AC=8,
∴AB==10,
∴sin A=.
9.解:∵四边形ABCD为矩形,
∴AD=BC,∠BAD=90°.
∵DE⊥AC,
∴∠ADE+∠DAE=90°.
而∠BAC+∠DAE=90°,
∴∠BAC=∠ADE=α.
在Rt△ABC中,∵sin∠BAC=,
∴.
设BC=4x,则AC=5x,
∴AB=3x,
∴3x=4,解得x=,
∴BC=
∴AD=.
课后提升
1.B 解析:∵在Rt△ABC中,∠C=90°,
∴cos B=.
∵AB=5,
∴BC=4,
∴AC==3.
故选B.
2.A 解析:如图,过B作BE∥AC交CD于点E.
∵AC⊥BC,
∴BE⊥BC,∴∠CBE=90°.
∵AB=BD,
∴AC=2BE.
又∵tan∠BCD=,设BE=x,则AC=2x,BC=3x,
∴tan A=,
故选A.
3.2 解析:∵CD是Rt△ABC斜边上的高线,
∴∠CDA=90°,∴∠A+∠ACD=90°.
又∵∠ACB=90°,∴∠ACD+∠BCD=90°,
∴∠A=∠BCD.
∵sin A=,
∴sin ∠BCD=.
∵BD=1,
∴BC=,
∴CD=.
∵sin A=,
∴AC=.
∴AD==2.
4.8或4 解析:①当∠ACB为锐角时,如图1,过点A作AD⊥BC,垂足为D.
图1
在Rt△ABD中,∵∠ABC=30°,AB=4,
∴AD=AB=2,BD=cos 30°×AB=6.
在Rt△ADC中,DC==2,
∴BC=BD+DC=6+2=8.
②当∠ACB为钝角时,如图2,过点A作AD⊥BC,交BC的延长线于点D.
图2
在Rt△ABD中,∵∠ABC=30°,AB=4,
∴AD=AB=2,BD=cos 30°×AB=6,
在Rt△ADC中,DC==2,
∴BC=BD-DC=6-2=4.
综上所述,BC的长为8或4.
5.解:(1)在Rt△ABC中,
∵sin C=,
∴∠C=30°,
∴∠CAB=90°-30°=60°.
(2)在Rt△ABC中,∠C=30°,
cos C=,
即,
∴BC=3,
∴CD=BC-BD=3-3.
6.解:过点A作AD⊥CB,垂足为点D,如图,
∵sin B=,∴.
∵AB=5,∴AD=4,∴BD=3.
∵AB=AF,AD⊥CB,
∴BF=2BD=6.
∵EF⊥CB,AD⊥CB,
∴EF∥AD,
∴.
∵AE∶EC=3∶5,DF=BD=3,
∴CF=5,∴CD=8.
在Rt△ACD中,AC==4,
∴sin C=.
7.解:(1)证明:∵AD是BC边上的中线,
∴BD=CD.
∵点E是AD的中点,
∴AE=ED.
∵AF∥BC,
∴∠AFE=∠DBE,∠FAE=∠BDE.
在△AFE和△DBE中,
∴△AFE≌△DBE(AAS),
∴AF=BD,
∴AF=DC.
又∵AF∥BC,
∴四边形ADCF为平行四边形.
∵AB=AC,AD为BC边上的中线,
∴AD⊥BC,
∴∠ADC=90°,
∴四边形ADCF为矩形.
(2)∵BC=6,AD为BC边上的中线,
∴BD=BC=3.
∵在Rt△ABD中,sin∠BAD=,
∴AB==5,
∴AD==4.
又∵点E为AD的中点,
∴ED=AD=2,
∴在Rt△EBD中,BE=,
∴EF=BE=.
