1.5 三角函数的应用 课时作业(含答案) 2024-2025学年数学北师大版九年级下册
文档属性
| 名称 | 1.5 三角函数的应用 课时作业(含答案) 2024-2025学年数学北师大版九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 158.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-26 21:18:49 | ||
图片预览



文档简介
5 三角函数的应用
方位角在三角函数中的应用
1.如图,一条东西向的大道上,A,B两景点相距20 km,C景点位于A景点北偏东60°方向上,位于B景点北偏西30°方向上,则A,C两景点相距 ( )
A.10 km B.10 km C.10 km D. km
2.(2024本溪月考)如图,l是南北方向的海岸线,码头A与灯塔B相距24 km,海岛C位于码头A北偏东60°方向.一艘勘测船从海岛C沿北偏西30°方向往灯塔B行驶,沿线勘测石油资源,勘测发现位于码头A北偏东15°方向的D处石油资源丰富.若规划修建从D处到海岸线的输油管道,则输油管道的最短长度是多少 (结果保留根号)
仰角、俯角在三角函数中的应用
3.如图,在一艘小船A上测得海岸上高为36 m的灯塔BC的顶部C处的仰角是30°,则船离灯塔的水平距离AB等于 ( )
A.36 m B.12 m C.18 m D.36 m
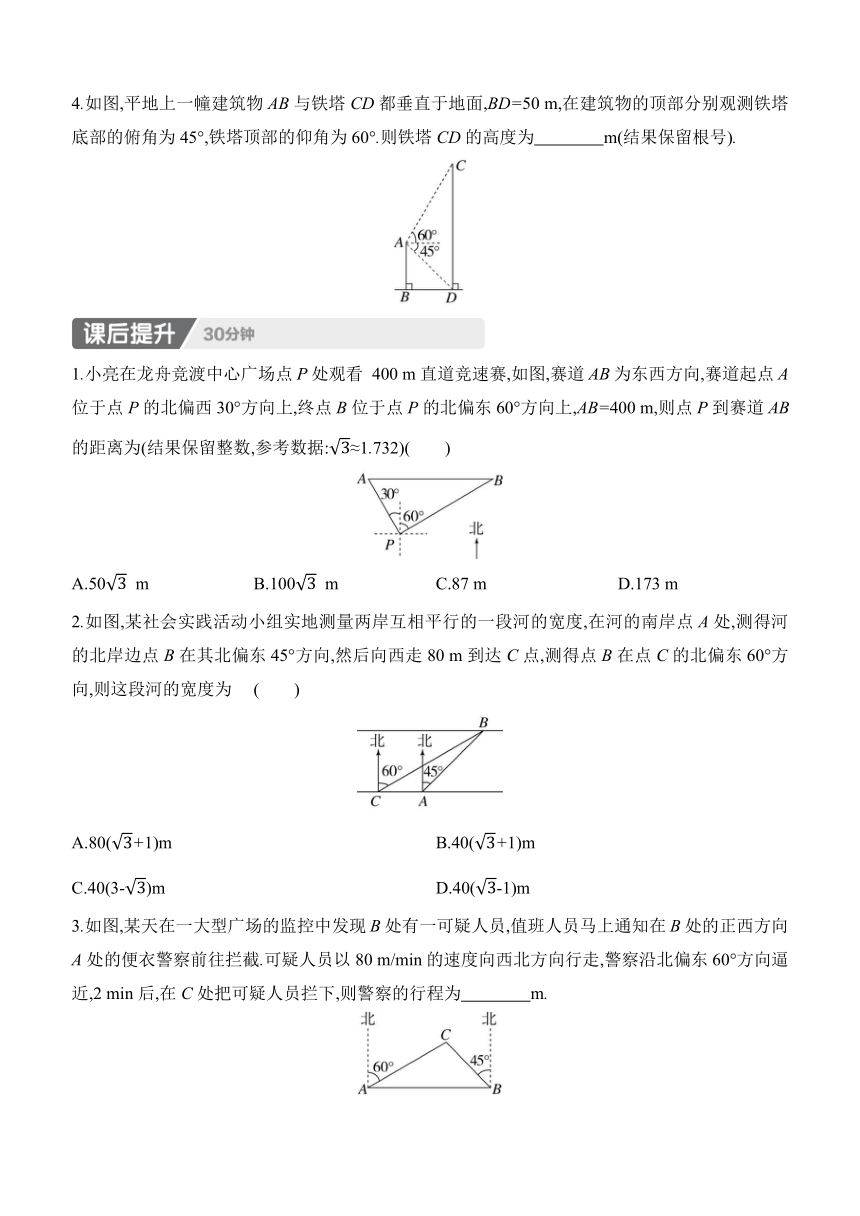
4.如图,平地上一幢建筑物AB与铁塔CD都垂直于地面,BD=50 m,在建筑物的顶部分别观测铁塔底部的俯角为45°,铁塔顶部的仰角为60°.则铁塔CD的高度为 m(结果保留根号).
1.小亮在龙舟竞渡中心广场点P处观看 400 m直道竞速赛,如图,赛道AB为东西方向,赛道起点A位于点P的北偏西30°方向上,终点B位于点P的北偏东60°方向上,AB=400 m,则点P到赛道AB的距离为(结果保留整数,参考数据:≈1.732)( )
A.50 m B.100 m C.87 m D.173 m
2.如图,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走80 m到达C点,测得点B在点C的北偏东60°方向,则这段河的宽度为 ( )
A.80(+1)m B.40(+1)m
C.40(3-)m D.40(-1)m
3.如图,某天在一大型广场的监控中发现B处有一可疑人员,值班人员马上通知在B处的正西方向A处的便衣警察前往拦截.可疑人员以80 m/min的速度向西北方向行走,警察沿北偏东60°方向逼近,2 min后,在C处把可疑人员拦下,则警察的行程为 m.
4.如图,某小组要测量风景区内两座小山山顶之间的滑行索道(索道近似看成线段)AD的长度.在山脚下的M处测得左侧山顶A的仰角为53°,测得右侧山顶D的仰角为67°,已知左侧山高AB为800 m,在左侧山顶A处测得右侧山顶D的仰角为22°,求滑行索道AD的长度.(精确到0.1 m,图中的点A,B,C,D,M均在同一平面内,B,M,C在同一水平线上.参考数据:sin 53°≈0.80,cos 53°≈0.60,tan 53°≈1.33,sin 22°≈0.37,cos 22°≈0.93,tan 22°≈0.39,sin 67°≈0.92,cos 67°≈0.39,tan 67°≈2.36)
5.(应用意识)如图,某动物园三角形观赏区ABE紧邻四边形熊猫馆ABCD.经测量,点C在点B的正东方向,点A在点B的北偏东45°方向,点E在点B的正北方向且在点A的正西方向,点D在点A的正东方向且在点C的北偏东60°方向.AD长30 m,CD长40 m.(参考数据:≈1.41,≈1.73)
(1)求AB的长度(结果精确到1 m);
(2)天气炎热时,饲养员会在点D处为熊猫放置冰块帮助熊猫降温.熊猫甲从B出发沿B→A→D到达点D,熊猫乙从B出发沿B→C→D到达点D,请计算说明哪只熊猫选择的路线较近
【详解答案】
课堂达标
1.B 解析:根据题意可知:
∠CAB=30°,∠CBA=60°,
∴∠ACB=180°-(60°+30°)=90°,
∵AB=20 km,
∴AC=AB×cos 30°=20×=10(km).
∴A,C两景点相距10 km.
故选B.
2.解:如图,过点D作DE⊥AB,垂足为E.
由题意,得∠BAD=15°,∠BAC=60°,∠BCF=30°,AB∥FG,
∴∠ACG=∠BAC=60°,∠BCF=∠ABC=30°,
∴∠ACB=180°-∠ACG-∠BCF=90°.
∵在Rt△ABC中,∠ACB=90°,∠ABC=30°,AB=24 km,
∴AC=AB=12 km,
BC=AC=12 km.
在Rt△ACD中,
∠CAD=∠BAC-∠BAD=45°,
∴CD=AC·tan 45°=12 km,
∴BD=BC-CD=(12-12) km.
在Rt△BDE中,∠ABC=30°,
∴DE=BD=(6-6) km,
∴输油管道的最短长度是(6-6) km.
3.A 解析:由题意,得CB⊥AB,
在Rt△ABC中,BC=36 m,∠CAB=30°,
∴AB==36(m),
∴船离灯塔的水平距离AB等于36 m,
故选A.
4.(50+50) 解析:如图,过点A作AE⊥CD,垂足为E.
由题意,得AE=BD=50 m,
在Rt△ADE中,∠EAD=45°,
∴DE=AE·tan 45°=50 m.
在Rt△ACE中,∠CAE=60°,
∴CE=AE·tan 60°=50 m,
∴CD=DE+CE=(50+50)m,
∴铁塔CD的高度为(50+50)m.
课后提升
1.D 解析:如图,过点P作PC⊥AB,垂足为C.
设PC=x m,
在Rt△APC中,∠APC=30°,
∴AC=PC·tan 30°=x(m),
在Rt△CBP中,∠CPB=60°,
∴BC=CP·tan 60°=x(m).
∵AB=400 m,
∴AC+BC=400,
∴x+x=400,
∴x=100≈173,∴PC=173 m,
∴点P到赛道AB的距离约为173 m,
故选D.
2.B 解析:过点B作BD⊥CA交CA的延长线于点D,如图.
设BD=x m,
∵∠BCA=30°,
∴CD=x(m).
∵∠BAD=45°,
∴AD=BD=x m.
∵AC=80 m,∴x-x=80,
解得x==40(+1),
故这段河的宽度为40(+1)m.
故选B.
3.160 解析:如图,过点C作CD⊥AB于点D.
在Rt△BCD中,BC=80×2=160(m),∠BCD=45°,
∵cos∠BCD=,
∴CD=BC·cos∠BCD=160×=80(m).
在Rt△ACD中,∠CAD=30°,
则AC=2CD=160(m),
故警察的行程为160 m.
4.解:如图,过点A作AE⊥CD,垂足为E.
由题意,得AB=CE=800 m,AE=BC,
设CM=x m,
在Rt△ABM中,∠AMB=53°,
∴BM=≈≈601.50(m),
∴AE=BC=BM+CM=(x+601.50)m.
在Rt△DCM中,∠DMC=67°,
∴DC=CM·tan 67°≈2.36x(m).
在Rt△ADE中,∠DAE=22°,
∴DE=AE·tan 22°≈0.4(x+601.50)m.
∵DE+CE=CD,
∴0.4(x+601.50)+800=2.36x,
解得x≈530.92,
∴AE=530.92+601.50=1 132.42(m),
在Rt△ADE中,AD=≈≈1 217.7(m),
∴滑行索道AD的长度约为1 217.7 m.
5.解:(1)如图,过C作CH⊥DE于点H.
在Rt△CDH中,∠DCH=60°,∠DHC=90°,
∴∠D=30°.
∵CD=40 m,∴CH=CD=20 m.
∵∠E=∠EBC=∠CHE=90°,
∴四边形BCHE是矩形,
∴BE=CH=20 m.
∵∠ABE=45°,
∴AB=BE=20≈28(m),
∴AB的长约为28 m.
(2)∵∠DHC=90°,∠DCH=60°,
∴DH=CH=20 m.
∵∠E=90°,∠ABE=45°,
∴∠ABE=∠BAE=45°,∴AE=BE=20 m,
∵AD=30 m,
∴EH=AE+AD-DH=20+30-20=(50-20)m,
∴BC=EH=(50-20)m,
∴熊猫甲从B出发沿B→A→D到达点D的路程=20+30≈58(m),
熊猫乙从B出发沿B→C→D到达点D的路程=50-20+40=90-20≈55(m),
∵58>55,
∴熊猫乙选择的路线较近.
方位角在三角函数中的应用
1.如图,一条东西向的大道上,A,B两景点相距20 km,C景点位于A景点北偏东60°方向上,位于B景点北偏西30°方向上,则A,C两景点相距 ( )
A.10 km B.10 km C.10 km D. km
2.(2024本溪月考)如图,l是南北方向的海岸线,码头A与灯塔B相距24 km,海岛C位于码头A北偏东60°方向.一艘勘测船从海岛C沿北偏西30°方向往灯塔B行驶,沿线勘测石油资源,勘测发现位于码头A北偏东15°方向的D处石油资源丰富.若规划修建从D处到海岸线的输油管道,则输油管道的最短长度是多少 (结果保留根号)
仰角、俯角在三角函数中的应用
3.如图,在一艘小船A上测得海岸上高为36 m的灯塔BC的顶部C处的仰角是30°,则船离灯塔的水平距离AB等于 ( )
A.36 m B.12 m C.18 m D.36 m
4.如图,平地上一幢建筑物AB与铁塔CD都垂直于地面,BD=50 m,在建筑物的顶部分别观测铁塔底部的俯角为45°,铁塔顶部的仰角为60°.则铁塔CD的高度为 m(结果保留根号).
1.小亮在龙舟竞渡中心广场点P处观看 400 m直道竞速赛,如图,赛道AB为东西方向,赛道起点A位于点P的北偏西30°方向上,终点B位于点P的北偏东60°方向上,AB=400 m,则点P到赛道AB的距离为(结果保留整数,参考数据:≈1.732)( )
A.50 m B.100 m C.87 m D.173 m
2.如图,某社会实践活动小组实地测量两岸互相平行的一段河的宽度,在河的南岸点A处,测得河的北岸边点B在其北偏东45°方向,然后向西走80 m到达C点,测得点B在点C的北偏东60°方向,则这段河的宽度为 ( )
A.80(+1)m B.40(+1)m
C.40(3-)m D.40(-1)m
3.如图,某天在一大型广场的监控中发现B处有一可疑人员,值班人员马上通知在B处的正西方向A处的便衣警察前往拦截.可疑人员以80 m/min的速度向西北方向行走,警察沿北偏东60°方向逼近,2 min后,在C处把可疑人员拦下,则警察的行程为 m.
4.如图,某小组要测量风景区内两座小山山顶之间的滑行索道(索道近似看成线段)AD的长度.在山脚下的M处测得左侧山顶A的仰角为53°,测得右侧山顶D的仰角为67°,已知左侧山高AB为800 m,在左侧山顶A处测得右侧山顶D的仰角为22°,求滑行索道AD的长度.(精确到0.1 m,图中的点A,B,C,D,M均在同一平面内,B,M,C在同一水平线上.参考数据:sin 53°≈0.80,cos 53°≈0.60,tan 53°≈1.33,sin 22°≈0.37,cos 22°≈0.93,tan 22°≈0.39,sin 67°≈0.92,cos 67°≈0.39,tan 67°≈2.36)
5.(应用意识)如图,某动物园三角形观赏区ABE紧邻四边形熊猫馆ABCD.经测量,点C在点B的正东方向,点A在点B的北偏东45°方向,点E在点B的正北方向且在点A的正西方向,点D在点A的正东方向且在点C的北偏东60°方向.AD长30 m,CD长40 m.(参考数据:≈1.41,≈1.73)
(1)求AB的长度(结果精确到1 m);
(2)天气炎热时,饲养员会在点D处为熊猫放置冰块帮助熊猫降温.熊猫甲从B出发沿B→A→D到达点D,熊猫乙从B出发沿B→C→D到达点D,请计算说明哪只熊猫选择的路线较近
【详解答案】
课堂达标
1.B 解析:根据题意可知:
∠CAB=30°,∠CBA=60°,
∴∠ACB=180°-(60°+30°)=90°,
∵AB=20 km,
∴AC=AB×cos 30°=20×=10(km).
∴A,C两景点相距10 km.
故选B.
2.解:如图,过点D作DE⊥AB,垂足为E.
由题意,得∠BAD=15°,∠BAC=60°,∠BCF=30°,AB∥FG,
∴∠ACG=∠BAC=60°,∠BCF=∠ABC=30°,
∴∠ACB=180°-∠ACG-∠BCF=90°.
∵在Rt△ABC中,∠ACB=90°,∠ABC=30°,AB=24 km,
∴AC=AB=12 km,
BC=AC=12 km.
在Rt△ACD中,
∠CAD=∠BAC-∠BAD=45°,
∴CD=AC·tan 45°=12 km,
∴BD=BC-CD=(12-12) km.
在Rt△BDE中,∠ABC=30°,
∴DE=BD=(6-6) km,
∴输油管道的最短长度是(6-6) km.
3.A 解析:由题意,得CB⊥AB,
在Rt△ABC中,BC=36 m,∠CAB=30°,
∴AB==36(m),
∴船离灯塔的水平距离AB等于36 m,
故选A.
4.(50+50) 解析:如图,过点A作AE⊥CD,垂足为E.
由题意,得AE=BD=50 m,
在Rt△ADE中,∠EAD=45°,
∴DE=AE·tan 45°=50 m.
在Rt△ACE中,∠CAE=60°,
∴CE=AE·tan 60°=50 m,
∴CD=DE+CE=(50+50)m,
∴铁塔CD的高度为(50+50)m.
课后提升
1.D 解析:如图,过点P作PC⊥AB,垂足为C.
设PC=x m,
在Rt△APC中,∠APC=30°,
∴AC=PC·tan 30°=x(m),
在Rt△CBP中,∠CPB=60°,
∴BC=CP·tan 60°=x(m).
∵AB=400 m,
∴AC+BC=400,
∴x+x=400,
∴x=100≈173,∴PC=173 m,
∴点P到赛道AB的距离约为173 m,
故选D.
2.B 解析:过点B作BD⊥CA交CA的延长线于点D,如图.
设BD=x m,
∵∠BCA=30°,
∴CD=x(m).
∵∠BAD=45°,
∴AD=BD=x m.
∵AC=80 m,∴x-x=80,
解得x==40(+1),
故这段河的宽度为40(+1)m.
故选B.
3.160 解析:如图,过点C作CD⊥AB于点D.
在Rt△BCD中,BC=80×2=160(m),∠BCD=45°,
∵cos∠BCD=,
∴CD=BC·cos∠BCD=160×=80(m).
在Rt△ACD中,∠CAD=30°,
则AC=2CD=160(m),
故警察的行程为160 m.
4.解:如图,过点A作AE⊥CD,垂足为E.
由题意,得AB=CE=800 m,AE=BC,
设CM=x m,
在Rt△ABM中,∠AMB=53°,
∴BM=≈≈601.50(m),
∴AE=BC=BM+CM=(x+601.50)m.
在Rt△DCM中,∠DMC=67°,
∴DC=CM·tan 67°≈2.36x(m).
在Rt△ADE中,∠DAE=22°,
∴DE=AE·tan 22°≈0.4(x+601.50)m.
∵DE+CE=CD,
∴0.4(x+601.50)+800=2.36x,
解得x≈530.92,
∴AE=530.92+601.50=1 132.42(m),
在Rt△ADE中,AD=≈≈1 217.7(m),
∴滑行索道AD的长度约为1 217.7 m.
5.解:(1)如图,过C作CH⊥DE于点H.
在Rt△CDH中,∠DCH=60°,∠DHC=90°,
∴∠D=30°.
∵CD=40 m,∴CH=CD=20 m.
∵∠E=∠EBC=∠CHE=90°,
∴四边形BCHE是矩形,
∴BE=CH=20 m.
∵∠ABE=45°,
∴AB=BE=20≈28(m),
∴AB的长约为28 m.
(2)∵∠DHC=90°,∠DCH=60°,
∴DH=CH=20 m.
∵∠E=90°,∠ABE=45°,
∴∠ABE=∠BAE=45°,∴AE=BE=20 m,
∵AD=30 m,
∴EH=AE+AD-DH=20+30-20=(50-20)m,
∴BC=EH=(50-20)m,
∴熊猫甲从B出发沿B→A→D到达点D的路程=20+30≈58(m),
熊猫乙从B出发沿B→C→D到达点D的路程=50-20+40=90-20≈55(m),
∵58>55,
∴熊猫乙选择的路线较近.
