1.6 利用三角函数测高 课时作业(含答案) 2024-2025学年数学北师大版九年级下册
文档属性
| 名称 | 1.6 利用三角函数测高 课时作业(含答案) 2024-2025学年数学北师大版九年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 181.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-26 21:18:53 | ||
图片预览


文档简介
6 利用三角函数测高
测量底部可以到达的物体的高度
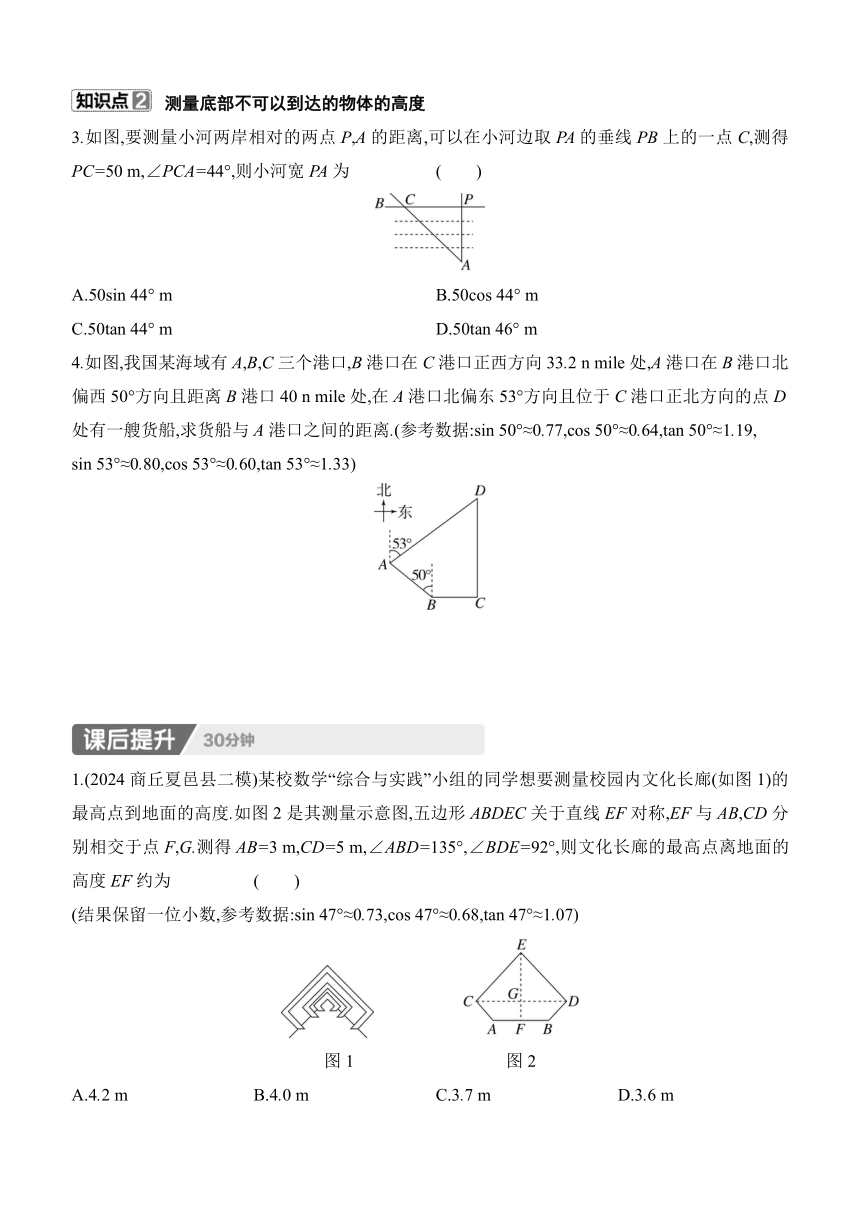
1.(2024大连甘井子区期末)如图,无人机在空中A处测得某校旗杆顶部B的仰角为30°,底部C的俯角为60°,无人机与旗杆的水平距离AD为6 m,则旗杆BC的高为 ( )
A.(3+6)m B.12m C.8m D.(6+2)m
2.某校活动小组借助无人机测量某纪念碑主碑AB的高度.如图,先将无人机升至距离地面10 m高的点C处,测得主碑最高点A的仰角∠MCA为37°,再将无人机从点C处竖直向上升高至距离地面15.8 m高的点D处,测得点A的俯角∠NDA为45°.已知点A,B,C,D,E在同一平面内,求纪念碑主碑AB的高度.(结果精确到0.1 m,参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75)
测量底部不可以到达的物体的高度
3.如图,要测量小河两岸相对的两点P,A的距离,可以在小河边取PA的垂线PB上的一点C,测得PC=50 m,∠PCA=44°,则小河宽PA为 ( )
A.50sin 44° m B.50cos 44° m
C.50tan 44° m D.50tan 46° m
4.如图,我国某海域有A,B,C三个港口,B港口在C港口正西方向33.2 n mile处,A港口在B港口北偏西50°方向且距离B港口40 n mile处,在A港口北偏东53°方向且位于C港口正北方向的点D处有一艘货船,求货船与A港口之间的距离.(参考数据:sin 50°≈0.77,cos 50°≈0.64,tan 50°≈1.19,
sin 53°≈0.80,cos 53°≈0.60,tan 53°≈1.33)
1.(2024商丘夏邑县二模)某校数学“综合与实践”小组的同学想要测量校园内文化长廊(如图1)的最高点到地面的高度.如图2是其测量示意图,五边形ABDEC关于直线EF对称,EF与AB,CD分别相交于点F,G.测得AB=3 m,CD=5 m,∠ABD=135°,∠BDE=92°,则文化长廊的最高点离地面的高度EF约为 ( )
(结果保留一位小数,参考数据:sin 47°≈0.73,cos 47°≈0.68,tan 47°≈1.07)
图1 图2
A.4.2 m B.4.0 m C.3.7 m D.3.6 m
2.如图,小张坐在某体育馆的观众席的C处目测(从他的眼睛D处看)得体育馆中心O处的俯角为18°,若CD=1.4 m,BC=1.5 m,BC平行于地面OA,台阶AB的坡度为3∶4,坡长AB=15 m,则观众席的底端A处与体育馆中心O处的距离约为 ( )
(参考数据:sin 18°≈0.31,cos 18°≈0.95,tan 18°≈0.32)
A.20 m B.19 m C.18 m D.17 m
3.如图,某校无人机兴趣小组为测量教学楼的高度,在操场上展开活动.此时无人机在离地面30 m的D处,操控者从A处观测无人机D的仰角为30°,无人机D测得教学楼BC顶端点C处的俯角为37°,又经过人工测量测得操控者A和教学楼BC之间的距离AB为60 m,点A,B,C,D都在同一平面上.
(1)求此时无人机D与教学楼BC之间的水平距离BE的长度(结果保留根号);
(2)求教学楼BC的高度(结果取整数.参考数据:≈1.73,sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75).
4.(应用意识)如图是某款篮球架的示意图,立柱OA垂直地面OB,支架CD与OA交于点A,支架CG⊥CD交OA于点G,支架DE平行地面OB,篮筐EF与支架DE在同一直线上,OA=2.5 m,AD=
0.8 m.∠AGC=32°.
(1)求∠GAC的度数;
(2)某运动员准备给篮筐挂上篮网,如果他站在凳子上,最高可以把篮网挂到离地面3 m处,那么他能挂上篮网吗 请通过计算说明理由.(参考数据:sin 32°≈0.53,cos 32°≈0.85,tan 32°≈0.62)
【详解答案】
课堂达标
1.C 解析:由题意,得AD⊥BC,
在Rt△ABD中,∠BAD=30°,AD=6 m,
∴BD=AD·tan 30°=6×=2(m).
在Rt△ACD中,∠DAC=60°,
∴CD=AD·tan 60°=6×=6(m),
∴BC=BD+CD=2+6=8(m),
故选C.
2.解:如图,过点A作AF⊥CD,垂足为F.
由题意,得AB=EF,CE=10 m,DE=15.8 m,AF∥CM∥DN,
∴CD=DE-CE=5.8 m,∠DAF=∠ADN=45°,∠ACM=∠FAC=37°.
设AF=x m,
在Rt△ACF中,CF=AF·tan 37°≈0.75x m,
在Rt△ADF中,DF=AF·tan 45°=x(m).
∵DF+CF=CD,
∴x+0.75x=5.8,
解得x=,
∴CF=0.75x=,
∴AB=EF=CE+CF=10+≈12.5(m),
∴纪念碑主碑AB的高度约为12.5 m.
3.C 解析:∵PA⊥PB,
∴∠APC=90°.
∵PC=50 m,∠PCA=44°,
∴tan 44°=,
∴小河宽PA=PCtan 44°=50tan 44°(m).
故选C.
4.解:如图,过点A作AE⊥CD,垂足为E,过点B作BF⊥AE,垂足为F.由题意,得
EF=BC=33.2 n mile,AG∥DC,
∴∠GAD=∠ADC=53°.
在Rt△ABF中,∠ABF=50°,AB=40 n mile,
∴AF=AB·sin 50°≈40×0.77=30.8(n mile),
∴AE=AF+EF=64 n mile.
在Rt△ADE中,AD=≈=80(n mile),
∴货船与A港口之间的距离约为80 n mile.
课后提升
1.C 解析:如图,过点B作BH⊥CD于点H.
由题意,得BF=AB=1.5 m,DG=CD=2.5 m.
∵EF垂直平分AB,垂足为F,EF垂直平分CD,与CD交于点G,BH⊥CD,
∴∠BFG=∠FGH=∠BHG=90°,
∴四边形GFBH为矩形,
∴GH=BF=1.5 m,∠FBH=90°,
∴DH=DG-GH=1 m.
∵∠ABD=135°,
∴∠DBH=45°,
∴BH=DH=GF=1 m.
∵∠BDE=92°,
∴∠EDG=47°,
在Rt△EDG中,tan∠EDG=,
∴EG=DGtan 47°≈2.5×1.07≈2.68(m),
∴EF=EG+GF≈2.68+1≈3.7(m),
故选C.
2.B 解析:如图,延长DC交OA的延长线于点F,
根据题意可知:DF⊥OA,
过点B作BG⊥OA交OA的延长线于点G,
则四边形BCFG是矩形,
∴CF=BG,FG=BC=1.5 m,
∵AB的坡度为3∶4,坡长AB=15 m,
∴BG=9 m,AG=12 m,
∵在Rt△ODF中,∠DOF=18°,
OF=OA+AG+GF=OA+12+1.5=13.5+OA,
DF=DC+CF=1.4+9=10.4(m),
∴DF=OF·tan 18°,
即10.4≈(13.5+OA)×0.32,
解得OA≈19.
∴观众席的底端A处与体育馆中心O处的距离约为19 m.
故选B.
3.解:(1)在Rt△ADE中,∠A=30°,DE=30 m,
∴AE=DE=30(m).
∵AB=60 m,
∴BE=AB-AE=(60-30)m,
∴此时无人机D与教学楼BC之间的水平距离BE的长度为(60-30)m.
(2)如图,过点C作CF⊥DE,垂足为F.
由题意,得CF=BE=(60-30)m,BC=EF,CF∥DG,
∴∠DCF=∠CDG=37°,
在Rt△DCF中,DF=CF·tan 37°≈(60-30)×0.75=m,
∴EF=DE-DF=30--15≈24(m),
∴BC=EF=24 m,
∴教学楼BC的高度约为24 m.
4.解:(1)∵CG⊥CD,
∴∠ACG=90°.
∵∠AGC=32°,
∴∠GAC=90°-∠AGC=90°-32°=58°,
∴∠GAC的度数为58°.
(2)该运动员能挂上篮网,
理由如下:如图,延长OA,ED交于点M.
∵OA⊥OB,
∴∠AOB=90°.
∵DE∥OB,
∴∠DMA=∠AOB=90°.
∵∠GAC=58°,
∴∠DAM=∠GAC=58°,
∴∠ADM=90°-∠DAM=32°,
在Rt△ADM中,AD=0.8 m,
∴AM=AD·sin 32°≈0.8×0.53=0.424(m),
∴OM=OA+AM=2.5+0.424=2.924(m).
∵2.924 m<3 m,
∴该运动员能挂上篮网.
测量底部可以到达的物体的高度
1.(2024大连甘井子区期末)如图,无人机在空中A处测得某校旗杆顶部B的仰角为30°,底部C的俯角为60°,无人机与旗杆的水平距离AD为6 m,则旗杆BC的高为 ( )
A.(3+6)m B.12m C.8m D.(6+2)m
2.某校活动小组借助无人机测量某纪念碑主碑AB的高度.如图,先将无人机升至距离地面10 m高的点C处,测得主碑最高点A的仰角∠MCA为37°,再将无人机从点C处竖直向上升高至距离地面15.8 m高的点D处,测得点A的俯角∠NDA为45°.已知点A,B,C,D,E在同一平面内,求纪念碑主碑AB的高度.(结果精确到0.1 m,参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75)
测量底部不可以到达的物体的高度
3.如图,要测量小河两岸相对的两点P,A的距离,可以在小河边取PA的垂线PB上的一点C,测得PC=50 m,∠PCA=44°,则小河宽PA为 ( )
A.50sin 44° m B.50cos 44° m
C.50tan 44° m D.50tan 46° m
4.如图,我国某海域有A,B,C三个港口,B港口在C港口正西方向33.2 n mile处,A港口在B港口北偏西50°方向且距离B港口40 n mile处,在A港口北偏东53°方向且位于C港口正北方向的点D处有一艘货船,求货船与A港口之间的距离.(参考数据:sin 50°≈0.77,cos 50°≈0.64,tan 50°≈1.19,
sin 53°≈0.80,cos 53°≈0.60,tan 53°≈1.33)
1.(2024商丘夏邑县二模)某校数学“综合与实践”小组的同学想要测量校园内文化长廊(如图1)的最高点到地面的高度.如图2是其测量示意图,五边形ABDEC关于直线EF对称,EF与AB,CD分别相交于点F,G.测得AB=3 m,CD=5 m,∠ABD=135°,∠BDE=92°,则文化长廊的最高点离地面的高度EF约为 ( )
(结果保留一位小数,参考数据:sin 47°≈0.73,cos 47°≈0.68,tan 47°≈1.07)
图1 图2
A.4.2 m B.4.0 m C.3.7 m D.3.6 m
2.如图,小张坐在某体育馆的观众席的C处目测(从他的眼睛D处看)得体育馆中心O处的俯角为18°,若CD=1.4 m,BC=1.5 m,BC平行于地面OA,台阶AB的坡度为3∶4,坡长AB=15 m,则观众席的底端A处与体育馆中心O处的距离约为 ( )
(参考数据:sin 18°≈0.31,cos 18°≈0.95,tan 18°≈0.32)
A.20 m B.19 m C.18 m D.17 m
3.如图,某校无人机兴趣小组为测量教学楼的高度,在操场上展开活动.此时无人机在离地面30 m的D处,操控者从A处观测无人机D的仰角为30°,无人机D测得教学楼BC顶端点C处的俯角为37°,又经过人工测量测得操控者A和教学楼BC之间的距离AB为60 m,点A,B,C,D都在同一平面上.
(1)求此时无人机D与教学楼BC之间的水平距离BE的长度(结果保留根号);
(2)求教学楼BC的高度(结果取整数.参考数据:≈1.73,sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75).
4.(应用意识)如图是某款篮球架的示意图,立柱OA垂直地面OB,支架CD与OA交于点A,支架CG⊥CD交OA于点G,支架DE平行地面OB,篮筐EF与支架DE在同一直线上,OA=2.5 m,AD=
0.8 m.∠AGC=32°.
(1)求∠GAC的度数;
(2)某运动员准备给篮筐挂上篮网,如果他站在凳子上,最高可以把篮网挂到离地面3 m处,那么他能挂上篮网吗 请通过计算说明理由.(参考数据:sin 32°≈0.53,cos 32°≈0.85,tan 32°≈0.62)
【详解答案】
课堂达标
1.C 解析:由题意,得AD⊥BC,
在Rt△ABD中,∠BAD=30°,AD=6 m,
∴BD=AD·tan 30°=6×=2(m).
在Rt△ACD中,∠DAC=60°,
∴CD=AD·tan 60°=6×=6(m),
∴BC=BD+CD=2+6=8(m),
故选C.
2.解:如图,过点A作AF⊥CD,垂足为F.
由题意,得AB=EF,CE=10 m,DE=15.8 m,AF∥CM∥DN,
∴CD=DE-CE=5.8 m,∠DAF=∠ADN=45°,∠ACM=∠FAC=37°.
设AF=x m,
在Rt△ACF中,CF=AF·tan 37°≈0.75x m,
在Rt△ADF中,DF=AF·tan 45°=x(m).
∵DF+CF=CD,
∴x+0.75x=5.8,
解得x=,
∴CF=0.75x=,
∴AB=EF=CE+CF=10+≈12.5(m),
∴纪念碑主碑AB的高度约为12.5 m.
3.C 解析:∵PA⊥PB,
∴∠APC=90°.
∵PC=50 m,∠PCA=44°,
∴tan 44°=,
∴小河宽PA=PCtan 44°=50tan 44°(m).
故选C.
4.解:如图,过点A作AE⊥CD,垂足为E,过点B作BF⊥AE,垂足为F.由题意,得
EF=BC=33.2 n mile,AG∥DC,
∴∠GAD=∠ADC=53°.
在Rt△ABF中,∠ABF=50°,AB=40 n mile,
∴AF=AB·sin 50°≈40×0.77=30.8(n mile),
∴AE=AF+EF=64 n mile.
在Rt△ADE中,AD=≈=80(n mile),
∴货船与A港口之间的距离约为80 n mile.
课后提升
1.C 解析:如图,过点B作BH⊥CD于点H.
由题意,得BF=AB=1.5 m,DG=CD=2.5 m.
∵EF垂直平分AB,垂足为F,EF垂直平分CD,与CD交于点G,BH⊥CD,
∴∠BFG=∠FGH=∠BHG=90°,
∴四边形GFBH为矩形,
∴GH=BF=1.5 m,∠FBH=90°,
∴DH=DG-GH=1 m.
∵∠ABD=135°,
∴∠DBH=45°,
∴BH=DH=GF=1 m.
∵∠BDE=92°,
∴∠EDG=47°,
在Rt△EDG中,tan∠EDG=,
∴EG=DGtan 47°≈2.5×1.07≈2.68(m),
∴EF=EG+GF≈2.68+1≈3.7(m),
故选C.
2.B 解析:如图,延长DC交OA的延长线于点F,
根据题意可知:DF⊥OA,
过点B作BG⊥OA交OA的延长线于点G,
则四边形BCFG是矩形,
∴CF=BG,FG=BC=1.5 m,
∵AB的坡度为3∶4,坡长AB=15 m,
∴BG=9 m,AG=12 m,
∵在Rt△ODF中,∠DOF=18°,
OF=OA+AG+GF=OA+12+1.5=13.5+OA,
DF=DC+CF=1.4+9=10.4(m),
∴DF=OF·tan 18°,
即10.4≈(13.5+OA)×0.32,
解得OA≈19.
∴观众席的底端A处与体育馆中心O处的距离约为19 m.
故选B.
3.解:(1)在Rt△ADE中,∠A=30°,DE=30 m,
∴AE=DE=30(m).
∵AB=60 m,
∴BE=AB-AE=(60-30)m,
∴此时无人机D与教学楼BC之间的水平距离BE的长度为(60-30)m.
(2)如图,过点C作CF⊥DE,垂足为F.
由题意,得CF=BE=(60-30)m,BC=EF,CF∥DG,
∴∠DCF=∠CDG=37°,
在Rt△DCF中,DF=CF·tan 37°≈(60-30)×0.75=m,
∴EF=DE-DF=30--15≈24(m),
∴BC=EF=24 m,
∴教学楼BC的高度约为24 m.
4.解:(1)∵CG⊥CD,
∴∠ACG=90°.
∵∠AGC=32°,
∴∠GAC=90°-∠AGC=90°-32°=58°,
∴∠GAC的度数为58°.
(2)该运动员能挂上篮网,
理由如下:如图,延长OA,ED交于点M.
∵OA⊥OB,
∴∠AOB=90°.
∵DE∥OB,
∴∠DMA=∠AOB=90°.
∵∠GAC=58°,
∴∠DAM=∠GAC=58°,
∴∠ADM=90°-∠DAM=32°,
在Rt△ADM中,AD=0.8 m,
∴AM=AD·sin 32°≈0.8×0.53=0.424(m),
∴OM=OA+AM=2.5+0.424=2.924(m).
∵2.924 m<3 m,
∴该运动员能挂上篮网.
