3.1 圆 课时作业 (含答案)2024-2025学年数学北师大版九年级下册
文档属性
| 名称 | 3.1 圆 课时作业 (含答案)2024-2025学年数学北师大版九年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 203.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-26 21:19:56 | ||
图片预览


文档简介
1圆
圆的有关概念
1.“车轮为什么都做成圆形 ”下面解释最合理的是 ( )
A.圆形是轴对称图形
B.圆形特别美观大方
C.圆形是曲线图形
D.从圆心到圆上任意一点的距离都相等
2.下列说法正确的是 ( )
A.大于半圆的弧叫做优弧
B.长度相等的两条弧叫做等弧
C.过圆心的线段是直径
D.直径一定大于弦
3.如图,A,B,C是☉O上三点,∠A=80°,∠C=60°,则∠B的大小为 .
4.(2024宿迁沭阳县月考)如图,在☉O中,AB是直径,CD是弦,延长AB,CD相交于点P,且AB=2DP,∠P=18°,求∠AOC的度数.
点和圆的位置关系
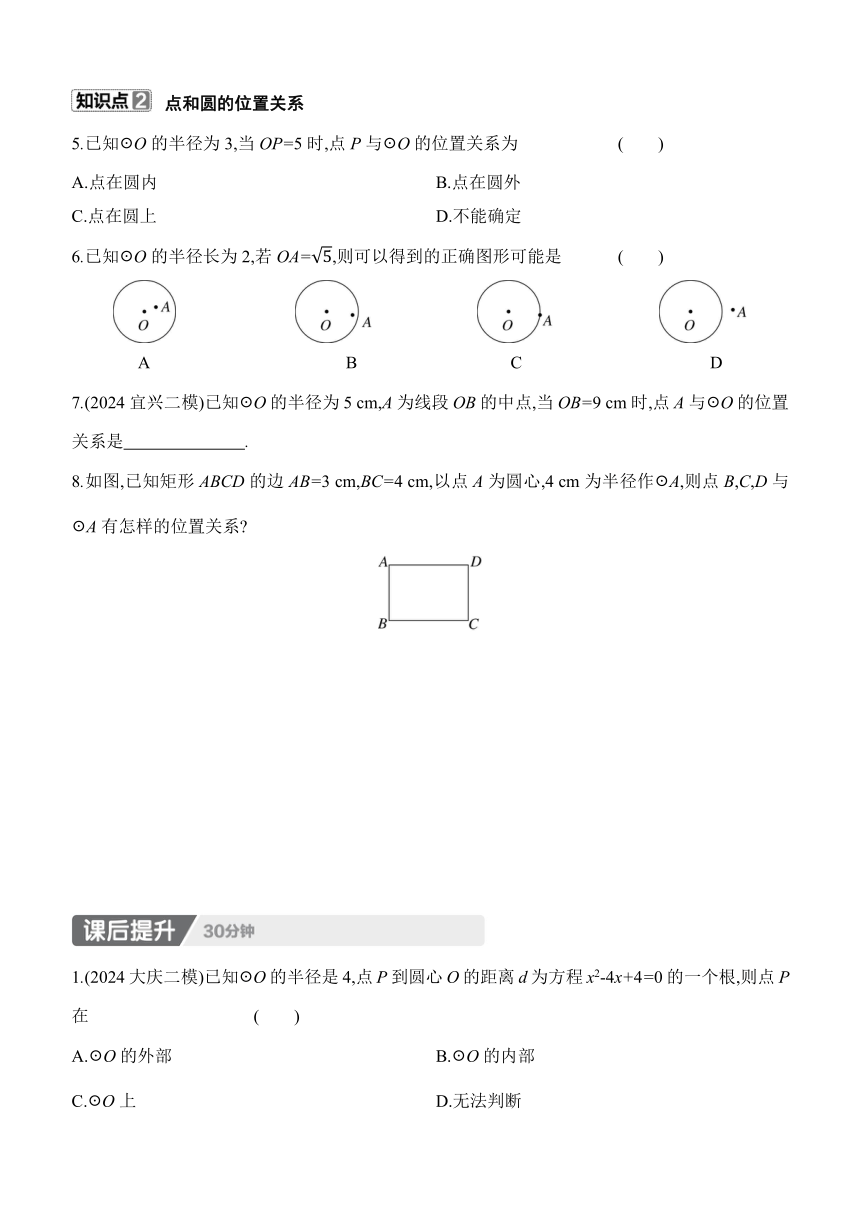
5.已知☉O的半径为3,当OP=5时,点P与☉O的位置关系为 ( )
A.点在圆内 B.点在圆外
C.点在圆上 D.不能确定
6.已知☉O的半径长为2,若OA=,则可以得到的正确图形可能是 ( )
A B C D
7.(2024宜兴二模)已知☉O的半径为5 cm,A为线段OB的中点,当OB=9 cm时,点A与☉O的位置关系是 .
8.如图,已知矩形ABCD的边AB=3 cm,BC=4 cm,以点A为圆心,4 cm为半径作☉A,则点B,C,D与☉A有怎样的位置关系
1.(2024大庆二模)已知☉O的半径是4,点P到圆心O的距离d为方程x2-4x+4=0的一个根,则点P在 ( )
A.☉O的外部 B.☉O的内部
C.☉O上 D.无法判断
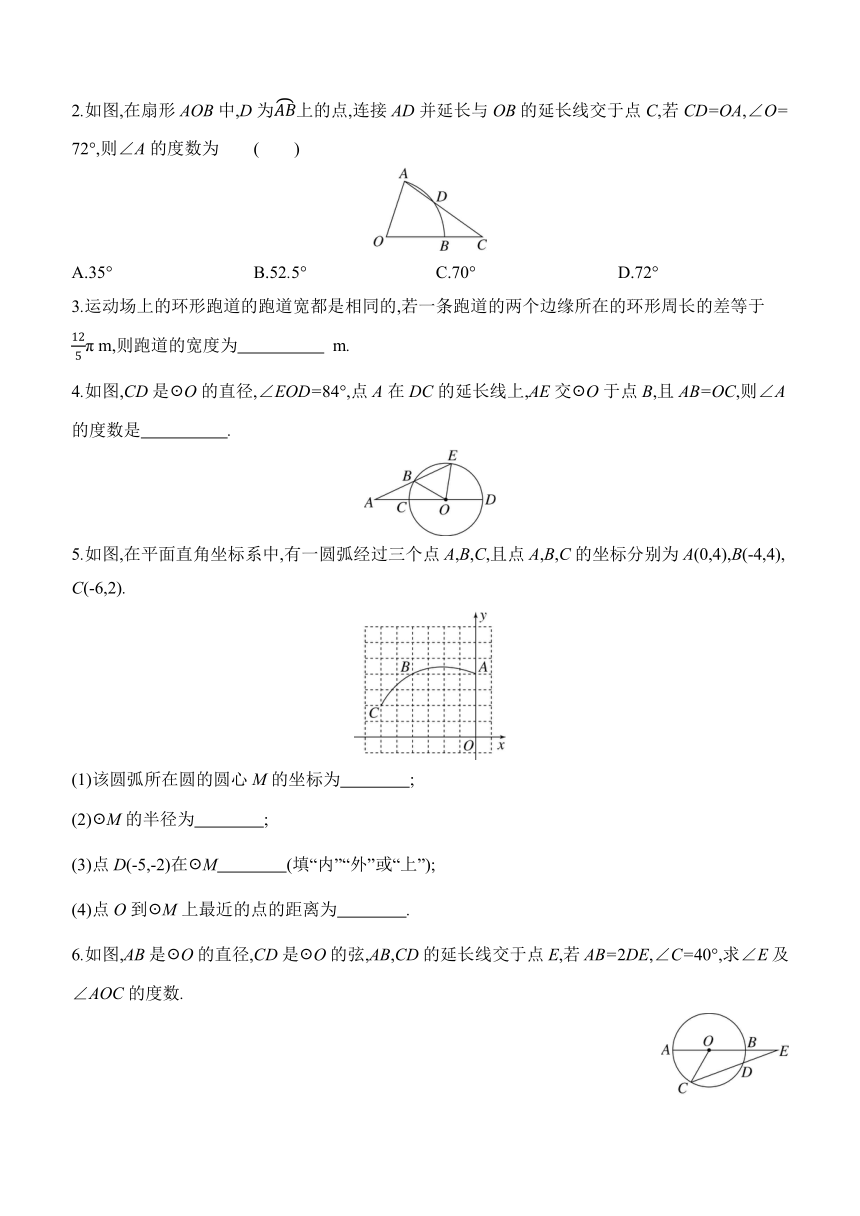
2.如图,在扇形AOB中,D为上的点,连接AD并延长与OB的延长线交于点C,若CD=OA,∠O=
72°,则∠A的度数为 ( )
A.35° B.52.5° C.70° D.72°
3.运动场上的环形跑道的跑道宽都是相同的,若一条跑道的两个边缘所在的环形周长的差等于
π m,则跑道的宽度为 m.
4.如图,CD是☉O的直径,∠EOD=84°,点A在DC的延长线上,AE交☉O于点B,且AB=OC,则∠A的度数是 .
5.如图,在平面直角坐标系中,有一圆弧经过三个点A,B,C,且点A,B,C的坐标分别为A(0,4),B(-4,4),
C(-6,2).
(1)该圆弧所在圆的圆心M的坐标为 ;
(2)☉M的半径为 ;
(3)点D(-5,-2)在☉M (填“内”“外”或“上”);
(4)点O到☉M上最近的点的距离为 .
6.如图,AB是☉O的直径,CD是☉O的弦,AB,CD的延长线交于点E,若AB=2DE,∠C=40°,求∠E及∠AOC的度数.
7.(推理能力)如图,E是菱形ABCD内一点,∠BEC=90°,DF⊥CE,垂足为F,且DF=CE,连接AE.
(1)求证:菱形ABCD是正方形;
(2)当F是线段CE的中点时,求证:点F在以AB为半径的☉A上.
【详解答案】
课堂达标
1.D 解析:车轮都做成圆形,利用了圆心到圆上任意一点的距离都相等,即圆半径都相等,即车轮滚动时车轴到地面的距离不变,这样子车子才不会颠簸,车子才会更平稳.
故选D.
2.A 解析:A.大于半圆的弧叫做优弧,原说法正确,符合题意;
B.在同圆或等圆中长度相等的两条弧叫做等弧,原说法错误,不符合题意;
C.过圆心的弦是直径,原说法错误,不符合题意;
D.在同圆或等圆中,直径一定大于除直径外的弦,原说法错误,不符合题意.
故选A.
3.140° 解析:连接OB,如图,
∵OA=OB,
∴∠A=∠OBA=80°.
∵OB=OC,
∴∠OBC=∠C=60°,
∴∠ABC=∠OBA+∠OBC=80°+60°=140°.
4.解:如图,连接OD,
∵AB=2DP=2OD,∠P=18°,
∴OD=DP,
∴∠DOP=∠P=18°.
∵∠ODC是△OPD的外角,
∴∠ODC=∠P+∠DOP=18°+18°=36°.
∵OD=OC,
∴∠OCD=∠ODC=36°,
∴∠COD=180°-36°-36°=108°,
∴∠AOC=180°-∠COD-∠DOP=180°-108°-18°=54°.
5.B 解析:∵OP=5,r=3,
∴OP>r,
则点P在☉O外.
故选B.
6.D 解析:∵☉O的半径为2,OA=,且>2,
∴点A在圆外.
故选D.
7.点A在☉O内 解析:∵A为线段OB的中点,∴当OB=9 cm时,
得OA=OB=4.5 cm.
∵r=5 cm,∴OA∴点A与☉O的位置关系是点A在☉O内.
8.解:如图,连接AC,
∵AB=3 cm,BC=AD=4 cm,
∴AC=5 cm,
∴点B在☉A内,点D在☉A上,点C在☉A外.
课后提升
1.B 解析:x2-4x+4=0可化为(x-2)2=0,
解得x=2,
∴OP=2.
∵2<4,
∴点P在☉O内.
故选B.
2.D 解析:连接OD,如图,设∠C的度数为n,
∵CD=OA=OD,
∴∠C=∠DOC=n,
∴∠ADO=∠DOC+∠C=2n.
∵OA=OD,
∴∠A=∠ADO=2n.
∵∠AOC+∠C+∠A=180°,∠AOC=72°,
∴72°+n+2n=180°,
解得n=36°,
∴∠A=2n=72°.
故选D.
3. 解析:设运动场上的小环半径为r m,大环半径为R m,根据题意,得
2π(R-r)=π,
解得R-r=,
即跑道的宽度为 m.
4.28° 解析:∵AB=OC,OC=OB,
∴AB=OB,
∴∠A=∠AOB.
∵BO=EO,
∴∠BEO=∠EBO.
由∠EBO是△ABO的外角,得
∠EBO=∠A+∠AOB=2∠A,
∴∠BEO=∠EBO=2∠A.
由∠DOE是△AOE的外角,得
∠A+∠AEO=∠EOD,
即∠A+2∠A=84°,
∴∠A=28°.
5.(1)(-2,0) (2)2 (3)内 (4)2-2
解析:(1)如图,分别作AB,BC的垂直平分线,两直线交于点M,
则点M即为该圆弧所在圆的圆心,
由图形可知,点M的坐标为(-2,0).
(2)☉M的半径长==2.
(3)MD=,<2,
∴MD<☉M的半径,
∴点D(-5,-2)在☉M内.
(4)由题意可得,点O到☉M上最近的点在直线OM上,
∵☉M的半径长为2,OM=2,
∴点O到☉M上最近的点的距离为2-2.
6.解:如图,连接OD,
∵OC=OD,∠C=40°,
∴∠ODC=∠C=40°.
∵AB=2DE,OD=AB,
∴OD=DE.
∵∠ODC是△DOE的外角,
∴∠E=∠EOD=∠ODC=20°.
∵∠AOC是△COE的外角,
∴∠AOC=∠C+∠E=40°+20°=60°.
7.证明:(1)∵DF⊥CE,
∴∠CFD=90°,
∴∠CDF+∠FCD=90°.
∵∠BEC=90°,
∴∠BEC=∠CFD.
∵四边形ABCD为菱形,
∴BC=CD.
在Rt△BCE和Rt△CDF中,
∴Rt△BCE≌Rt△CDF(HL),
∴∠BCE=∠CDF,
∴∠BCE+∠FCD=90°,
∴∠BCD=90°,
∴菱形ABCD为正方形.
(2)如图,连接AF,ED,
∵四边形ABCD为正方形,
∴∠ADC=90°,AD=CD.
∵F为CE的中点,DF⊥CE,
∴DF是CE的垂直平分线,
∴DE=DC=AD,
∴∠DAE=∠DEA,∠DEC=∠DCE.
∵∠DAE+∠DEA+∠ADE=180°,∠DEC+∠DCE+∠CDE=180°,
∴∠AED=,
∠DEC=,
∴∠AEF=∠AED+∠DEC=180°-(∠ADE+∠CDE)=180°-45°=135°,
∴∠AEB=360°-135°-90°=135°,
∴∠AEF=∠AEB.
∵△BCE≌△CDF,
∴BE=CF=FE.
在△AFE和△ABE中,
∴△AFE≌△ABE(SAS),∴AB=AF,
∴点F在以AB为半径的☉A上.
圆的有关概念
1.“车轮为什么都做成圆形 ”下面解释最合理的是 ( )
A.圆形是轴对称图形
B.圆形特别美观大方
C.圆形是曲线图形
D.从圆心到圆上任意一点的距离都相等
2.下列说法正确的是 ( )
A.大于半圆的弧叫做优弧
B.长度相等的两条弧叫做等弧
C.过圆心的线段是直径
D.直径一定大于弦
3.如图,A,B,C是☉O上三点,∠A=80°,∠C=60°,则∠B的大小为 .
4.(2024宿迁沭阳县月考)如图,在☉O中,AB是直径,CD是弦,延长AB,CD相交于点P,且AB=2DP,∠P=18°,求∠AOC的度数.
点和圆的位置关系
5.已知☉O的半径为3,当OP=5时,点P与☉O的位置关系为 ( )
A.点在圆内 B.点在圆外
C.点在圆上 D.不能确定
6.已知☉O的半径长为2,若OA=,则可以得到的正确图形可能是 ( )
A B C D
7.(2024宜兴二模)已知☉O的半径为5 cm,A为线段OB的中点,当OB=9 cm时,点A与☉O的位置关系是 .
8.如图,已知矩形ABCD的边AB=3 cm,BC=4 cm,以点A为圆心,4 cm为半径作☉A,则点B,C,D与☉A有怎样的位置关系
1.(2024大庆二模)已知☉O的半径是4,点P到圆心O的距离d为方程x2-4x+4=0的一个根,则点P在 ( )
A.☉O的外部 B.☉O的内部
C.☉O上 D.无法判断
2.如图,在扇形AOB中,D为上的点,连接AD并延长与OB的延长线交于点C,若CD=OA,∠O=
72°,则∠A的度数为 ( )
A.35° B.52.5° C.70° D.72°
3.运动场上的环形跑道的跑道宽都是相同的,若一条跑道的两个边缘所在的环形周长的差等于
π m,则跑道的宽度为 m.
4.如图,CD是☉O的直径,∠EOD=84°,点A在DC的延长线上,AE交☉O于点B,且AB=OC,则∠A的度数是 .
5.如图,在平面直角坐标系中,有一圆弧经过三个点A,B,C,且点A,B,C的坐标分别为A(0,4),B(-4,4),
C(-6,2).
(1)该圆弧所在圆的圆心M的坐标为 ;
(2)☉M的半径为 ;
(3)点D(-5,-2)在☉M (填“内”“外”或“上”);
(4)点O到☉M上最近的点的距离为 .
6.如图,AB是☉O的直径,CD是☉O的弦,AB,CD的延长线交于点E,若AB=2DE,∠C=40°,求∠E及∠AOC的度数.
7.(推理能力)如图,E是菱形ABCD内一点,∠BEC=90°,DF⊥CE,垂足为F,且DF=CE,连接AE.
(1)求证:菱形ABCD是正方形;
(2)当F是线段CE的中点时,求证:点F在以AB为半径的☉A上.
【详解答案】
课堂达标
1.D 解析:车轮都做成圆形,利用了圆心到圆上任意一点的距离都相等,即圆半径都相等,即车轮滚动时车轴到地面的距离不变,这样子车子才不会颠簸,车子才会更平稳.
故选D.
2.A 解析:A.大于半圆的弧叫做优弧,原说法正确,符合题意;
B.在同圆或等圆中长度相等的两条弧叫做等弧,原说法错误,不符合题意;
C.过圆心的弦是直径,原说法错误,不符合题意;
D.在同圆或等圆中,直径一定大于除直径外的弦,原说法错误,不符合题意.
故选A.
3.140° 解析:连接OB,如图,
∵OA=OB,
∴∠A=∠OBA=80°.
∵OB=OC,
∴∠OBC=∠C=60°,
∴∠ABC=∠OBA+∠OBC=80°+60°=140°.
4.解:如图,连接OD,
∵AB=2DP=2OD,∠P=18°,
∴OD=DP,
∴∠DOP=∠P=18°.
∵∠ODC是△OPD的外角,
∴∠ODC=∠P+∠DOP=18°+18°=36°.
∵OD=OC,
∴∠OCD=∠ODC=36°,
∴∠COD=180°-36°-36°=108°,
∴∠AOC=180°-∠COD-∠DOP=180°-108°-18°=54°.
5.B 解析:∵OP=5,r=3,
∴OP>r,
则点P在☉O外.
故选B.
6.D 解析:∵☉O的半径为2,OA=,且>2,
∴点A在圆外.
故选D.
7.点A在☉O内 解析:∵A为线段OB的中点,∴当OB=9 cm时,
得OA=OB=4.5 cm.
∵r=5 cm,∴OA
8.解:如图,连接AC,
∵AB=3 cm,BC=AD=4 cm,
∴AC=5 cm,
∴点B在☉A内,点D在☉A上,点C在☉A外.
课后提升
1.B 解析:x2-4x+4=0可化为(x-2)2=0,
解得x=2,
∴OP=2.
∵2<4,
∴点P在☉O内.
故选B.
2.D 解析:连接OD,如图,设∠C的度数为n,
∵CD=OA=OD,
∴∠C=∠DOC=n,
∴∠ADO=∠DOC+∠C=2n.
∵OA=OD,
∴∠A=∠ADO=2n.
∵∠AOC+∠C+∠A=180°,∠AOC=72°,
∴72°+n+2n=180°,
解得n=36°,
∴∠A=2n=72°.
故选D.
3. 解析:设运动场上的小环半径为r m,大环半径为R m,根据题意,得
2π(R-r)=π,
解得R-r=,
即跑道的宽度为 m.
4.28° 解析:∵AB=OC,OC=OB,
∴AB=OB,
∴∠A=∠AOB.
∵BO=EO,
∴∠BEO=∠EBO.
由∠EBO是△ABO的外角,得
∠EBO=∠A+∠AOB=2∠A,
∴∠BEO=∠EBO=2∠A.
由∠DOE是△AOE的外角,得
∠A+∠AEO=∠EOD,
即∠A+2∠A=84°,
∴∠A=28°.
5.(1)(-2,0) (2)2 (3)内 (4)2-2
解析:(1)如图,分别作AB,BC的垂直平分线,两直线交于点M,
则点M即为该圆弧所在圆的圆心,
由图形可知,点M的坐标为(-2,0).
(2)☉M的半径长==2.
(3)MD=,<2,
∴MD<☉M的半径,
∴点D(-5,-2)在☉M内.
(4)由题意可得,点O到☉M上最近的点在直线OM上,
∵☉M的半径长为2,OM=2,
∴点O到☉M上最近的点的距离为2-2.
6.解:如图,连接OD,
∵OC=OD,∠C=40°,
∴∠ODC=∠C=40°.
∵AB=2DE,OD=AB,
∴OD=DE.
∵∠ODC是△DOE的外角,
∴∠E=∠EOD=∠ODC=20°.
∵∠AOC是△COE的外角,
∴∠AOC=∠C+∠E=40°+20°=60°.
7.证明:(1)∵DF⊥CE,
∴∠CFD=90°,
∴∠CDF+∠FCD=90°.
∵∠BEC=90°,
∴∠BEC=∠CFD.
∵四边形ABCD为菱形,
∴BC=CD.
在Rt△BCE和Rt△CDF中,
∴Rt△BCE≌Rt△CDF(HL),
∴∠BCE=∠CDF,
∴∠BCE+∠FCD=90°,
∴∠BCD=90°,
∴菱形ABCD为正方形.
(2)如图,连接AF,ED,
∵四边形ABCD为正方形,
∴∠ADC=90°,AD=CD.
∵F为CE的中点,DF⊥CE,
∴DF是CE的垂直平分线,
∴DE=DC=AD,
∴∠DAE=∠DEA,∠DEC=∠DCE.
∵∠DAE+∠DEA+∠ADE=180°,∠DEC+∠DCE+∠CDE=180°,
∴∠AED=,
∠DEC=,
∴∠AEF=∠AED+∠DEC=180°-(∠ADE+∠CDE)=180°-45°=135°,
∴∠AEB=360°-135°-90°=135°,
∴∠AEF=∠AEB.
∵△BCE≌△CDF,
∴BE=CF=FE.
在△AFE和△ABE中,
∴△AFE≌△ABE(SAS),∴AB=AF,
∴点F在以AB为半径的☉A上.
