3.3 垂径定理课时作业(含答案) 2024-2025学年数学北师大版九年级下册
文档属性
| 名称 | 3.3 垂径定理课时作业(含答案) 2024-2025学年数学北师大版九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 213.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-26 00:00:00 | ||
图片预览




文档简介
*3垂径定理
垂径定理及其推论
1.如图,在☉O中,弦AB长6 cm,圆心O到AB的距离是3 cm,则☉O的半径是 ( )
A.3 cm B.3 cm C.4 cm D.3 cm
2.如图,☉O的半径是3,点P是弦AB延长线上的一点,连接OP,若OP=4,∠APO=30°,则弦AB的长为 .
3.如图,AB是☉O的直径,弦CD⊥AB于点E,若BE=5,CD=6,求AE的长.
4.(2024营口期中)如图,已知☉O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD.
求证:E是OB的中点.
利用垂径定理解决实际问题
5.如图,圆形输水管的横截面阴影部分为有水部分,水面AB宽为12 cm,水的最大深度为12 cm,则该输水管的半径为 ( )
A.5 cm B.6 cm
C.7.5 cm D.10 cm
6.如图,一个底部呈球形的烧瓶,瓶内液体的最大深度CD=2 cm,截面圆中弦AB长为10 cm,那么☉O的半径OB长为 .
7.如图,某地有一座圆弧形拱桥,其圆心为O,桥下水面宽度AB为7.2 m,拱高CD为2.4 m.
(1)求拱桥的半径;
(2)夏季雨季来临时,当水面离桥顶C距离为1 m时,就要禁止通行,某天暴雨后桥下水面宽度EF为3 m,请通过计算说明是否要禁止通行.
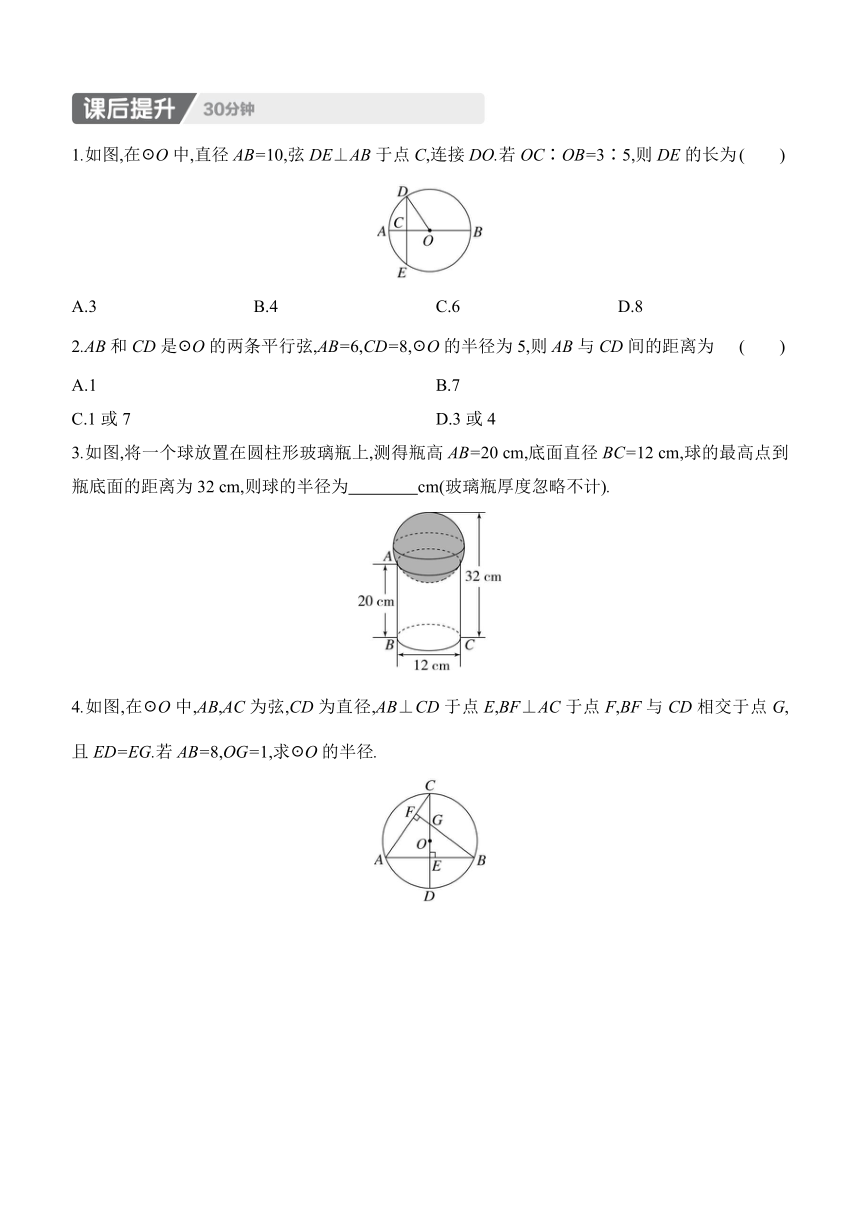
1.如图,在☉O中,直径AB=10,弦DE⊥AB于点C,连接DO.若OC∶OB=3∶5,则DE的长为 ( )
A.3 B.4 C.6 D.8
2.AB和CD是☉O的两条平行弦,AB=6,CD=8,☉O的半径为5,则AB与CD间的距离为 ( )
A.1 B.7
C.1或7 D.3或4
3.如图,将一个球放置在圆柱形玻璃瓶上,测得瓶高AB=20 cm,底面直径BC=12 cm,球的最高点到瓶底面的距离为32 cm,则球的半径为 cm(玻璃瓶厚度忽略不计).
4.如图,在☉O中,AB,AC为弦,CD为直径,AB⊥CD于点E,BF⊥AC于点F,BF与CD相交于点G,且ED=EG.若AB=8,OG=1,求☉O的半径.
5.(2024东莞一模)HUAWEI Mate60 Pro是华为技术有限公司于2023年8月29日上架的一款全球首款支持卫星通话的大众智能手机,手机背面有一条圆弧,象征着以山河之美致敬奔腾不息的力量.如图,圆弧对应的弦AB长80 mm,半径OC⊥AB,垂足为D,弓形高CD长14 mm.
(1)求AD的长;
(2)求半径OA的长.
6.(应用意识)如图1,圆形拱门屏风是中国古代家庭中常见的装饰隔断,既美观又实用,彰显出中国元素的韵味.图2是一款拱门的示意图,其中C为AB中点,D为拱门最高点,线段CD经过圆心,已知拱门的半径为1.5 m,拱门最下端AB=1.8 m.
(1)求拱门最高点D到地面的距离;
(2)现需要给房间内搬进一个长和宽为2 m,高为1.2 m的桌子,已知搬桌子的两名工人在搬运时所抬高度相同,且高度为0.5 m,判断搬运该桌子时是否能够通过拱门.(参考数据:≈2.236)
图1 图2
【详解答案】
课堂达标
1.B 解析:如图,
由题意知,OC=3,且OC⊥AB,
∵AB=6,
∴AC=AB=3,
则OA==3(cm).
故选B.
2.2 解析:如图,连接OB,过点O作OC⊥AB于点C,
则∠OCP=90°.
∵OP=4,∠APO=30°,
∴OC=OP=2.
在Rt△OCB中,由勾股定理,得BC=.
∵OC⊥AB,
∴AB=2BC=2.
3.解:如图,连接OC,
∵CD⊥AB,AB是直径,
∴CE=DE=CD=3.
设半径为r,则OE=5-r,OC=r,在Rt△COE中,由勾股定理,得
OE2+CE2=OC2,
即(5-r)2+32=r2,
解得r=3.4,
∴AE=AB-BE=3.4×2-5=1.8.
答:AE的长为1.8.
4.证明:如图,连接AC,
∵直径AB垂直于弦CD于点E,
∴,
∴AC=AD.
∵过圆心O的CF⊥AD,
∴,∴AC=CD,
∴AC=AD=CD.
∴△ACD是等边三角形,∴∠ACD=60°.
又∵CF⊥AD,
∴∠FCD=∠ACD=30°,
∴在Rt△COE中,OE=OC,
∴OE=OB,
∴点E为OB的中点.
5.C 解析:如图,设圆心为O,过点O作OD⊥AB于点D,DO的延长线交☉O于点C,连接OA,
∵OD⊥AB于点D,DO的延长线交☉O于点C,
∴水的最大深度为CD=12 cm,AD=AB=×12=6(cm).
设OA=r cm,则OD=(12-r)cm,
在Rt△AOD中,OA2=OD2+AD2,即r2=(12-r)2+62,
解得r=7.5.
故该输水管的半径为7.5 cm.
故选C.
6. cm 解析:根据题意,得AB⊥OD,
∴AC=BC=AB=5 cm.
∵OB=OD,
∴OC=OD-CD=(OB-2)cm.
在Rt△BOC中,OB2=OC2+BC2,
∴OB2=(OB-2)2+52,
∴OB=,故☉O的半径OB长为 cm.
7.解:(1)如图,连接OB,
∵OC⊥AB,
∴D为AB的中点.
∵AB=7.2 m,
∴BD=AB=3.6 m.
又∵CD=2.4 m,
设OB=OC=r m,则OD=(r-2.4)m,
在Rt△BOD中,根据勾股定理得r2=(r-2.4)2+3.62,
解得r=3.9.
答:拱桥的半径为3.9 m.
(2)如图,连接OF,
∵OC⊥EF,
∴G为EF的中点.
∵EF=3 m,
∴GF=EF=1.5 m.
∵OF=3.9 m,
在Rt△OFG中,OG2=OF2-GF2=3.92-1.52=12.96,
∴OG==3.6(m),
∴CG=OC-OG=3.9-3.6=0.3(m)<1 m,
∴要禁止通行.
课后提升
1.D 解析:∵AB=10,
∴OA=OB=5,
∵OC∶OB=3∶5,
∴OC=3.
在Rt△OCD中,CD==4.
∵DE⊥AB,∴DE=2CD=8.
故选D.
2.C 解析:①当AB,CD在圆心两侧时,
过点O作OE⊥CD于点E,OF⊥AB于点F,连接OA,OC,如图,
∵半径r=5,弦AB∥CD,且AB=6,CD=8,
∴OA=OC=5,CE=DE=4,AF=FB=3.∵E,F,O在一条直线上,
∴EF为AB、CD之间的距离,
在Rt△OEC中,由勾股定理,得
OE2=OC2-CE2,
∴OE==3.
在Rt△OFA中,由勾股定理,得
OF2=OA2-AF2,
∴OF==4,
∴EF=OE+OF=3+4=7,
∴AB与CD的距离为7.
②当AB,CD在圆心同侧时(图略),
同①可得OE=3,OF=4,
则AB与CD的距离为OF-OE=1.
综上所述,AB与CD间的距离为1或7.
故选C.
3.7.5 解析:如图,设球心为O,过点O作OM⊥AD于点M,连接OA,
设球的半径为r cm,
由题意,得AD=12 cm,OM=32-20-r=(12-r)(cm).
由垂径定理,得AM=DM=AD=6 cm.
在Rt△OAM中,由勾股定理,得AM2+OM2=OA2,
即62+(12-r)2=r2,
解得r=7.5,
即球的半径为7.5 cm.
4.解:如图,连接OA,
设OA=r,则DG=r+1,
∵ED=EG,∴ED=,
∴OE=OD-ED=.
∵AB⊥CD于点E,AB=8,
∴AE=BE=4,
∴在Rt△OAE中,根据勾股定理,得OE2+AE2=OA2,
即2+42=r2,
解得r=(负值舍去),
即☉O的半径为.
5.解:(1)∵OC⊥AB,AB=80 mm,
∴AD=AB=40 mm.
(2)∵OC⊥AB,∴∠ADO=90°,
设半径OA=x mm,
则OC=OA=x mm,OD=OC-CD=(x-14)mm,
∴AD2+OD2=OA2,
即402+(x-14)2=x2,
解得x=64,
∴半径OA的长为64 mm.
6.解:(1)如图1,连接AO.
图1
∵CD⊥AB,CD经过圆心O,
∴AC=CB=0.9 m,
∴OC==1.2 m,
∴CD=OD+OC=1.5+1.2=2.7(m),
∴拱门最高点D到地面的距离为2.7 m.
(2)如图2,弦EF=2 m,且EF⊥CD,连接OE.
图2
∵CD⊥EF,CD经过圆心,
∴EJ=JF=1 m,
∴OJ=≈1.118(m),
∴CJ=1.2-1.118=0.082(m),
∵0.5>0.082,
∴搬运该桌子时能够通过拱门.
垂径定理及其推论
1.如图,在☉O中,弦AB长6 cm,圆心O到AB的距离是3 cm,则☉O的半径是 ( )
A.3 cm B.3 cm C.4 cm D.3 cm
2.如图,☉O的半径是3,点P是弦AB延长线上的一点,连接OP,若OP=4,∠APO=30°,则弦AB的长为 .
3.如图,AB是☉O的直径,弦CD⊥AB于点E,若BE=5,CD=6,求AE的长.
4.(2024营口期中)如图,已知☉O的直径AB垂直于弦CD于点E,连接CO并延长交AD于点F,且CF⊥AD.
求证:E是OB的中点.
利用垂径定理解决实际问题
5.如图,圆形输水管的横截面阴影部分为有水部分,水面AB宽为12 cm,水的最大深度为12 cm,则该输水管的半径为 ( )
A.5 cm B.6 cm
C.7.5 cm D.10 cm
6.如图,一个底部呈球形的烧瓶,瓶内液体的最大深度CD=2 cm,截面圆中弦AB长为10 cm,那么☉O的半径OB长为 .
7.如图,某地有一座圆弧形拱桥,其圆心为O,桥下水面宽度AB为7.2 m,拱高CD为2.4 m.
(1)求拱桥的半径;
(2)夏季雨季来临时,当水面离桥顶C距离为1 m时,就要禁止通行,某天暴雨后桥下水面宽度EF为3 m,请通过计算说明是否要禁止通行.
1.如图,在☉O中,直径AB=10,弦DE⊥AB于点C,连接DO.若OC∶OB=3∶5,则DE的长为 ( )
A.3 B.4 C.6 D.8
2.AB和CD是☉O的两条平行弦,AB=6,CD=8,☉O的半径为5,则AB与CD间的距离为 ( )
A.1 B.7
C.1或7 D.3或4
3.如图,将一个球放置在圆柱形玻璃瓶上,测得瓶高AB=20 cm,底面直径BC=12 cm,球的最高点到瓶底面的距离为32 cm,则球的半径为 cm(玻璃瓶厚度忽略不计).
4.如图,在☉O中,AB,AC为弦,CD为直径,AB⊥CD于点E,BF⊥AC于点F,BF与CD相交于点G,且ED=EG.若AB=8,OG=1,求☉O的半径.
5.(2024东莞一模)HUAWEI Mate60 Pro是华为技术有限公司于2023年8月29日上架的一款全球首款支持卫星通话的大众智能手机,手机背面有一条圆弧,象征着以山河之美致敬奔腾不息的力量.如图,圆弧对应的弦AB长80 mm,半径OC⊥AB,垂足为D,弓形高CD长14 mm.
(1)求AD的长;
(2)求半径OA的长.
6.(应用意识)如图1,圆形拱门屏风是中国古代家庭中常见的装饰隔断,既美观又实用,彰显出中国元素的韵味.图2是一款拱门的示意图,其中C为AB中点,D为拱门最高点,线段CD经过圆心,已知拱门的半径为1.5 m,拱门最下端AB=1.8 m.
(1)求拱门最高点D到地面的距离;
(2)现需要给房间内搬进一个长和宽为2 m,高为1.2 m的桌子,已知搬桌子的两名工人在搬运时所抬高度相同,且高度为0.5 m,判断搬运该桌子时是否能够通过拱门.(参考数据:≈2.236)
图1 图2
【详解答案】
课堂达标
1.B 解析:如图,
由题意知,OC=3,且OC⊥AB,
∵AB=6,
∴AC=AB=3,
则OA==3(cm).
故选B.
2.2 解析:如图,连接OB,过点O作OC⊥AB于点C,
则∠OCP=90°.
∵OP=4,∠APO=30°,
∴OC=OP=2.
在Rt△OCB中,由勾股定理,得BC=.
∵OC⊥AB,
∴AB=2BC=2.
3.解:如图,连接OC,
∵CD⊥AB,AB是直径,
∴CE=DE=CD=3.
设半径为r,则OE=5-r,OC=r,在Rt△COE中,由勾股定理,得
OE2+CE2=OC2,
即(5-r)2+32=r2,
解得r=3.4,
∴AE=AB-BE=3.4×2-5=1.8.
答:AE的长为1.8.
4.证明:如图,连接AC,
∵直径AB垂直于弦CD于点E,
∴,
∴AC=AD.
∵过圆心O的CF⊥AD,
∴,∴AC=CD,
∴AC=AD=CD.
∴△ACD是等边三角形,∴∠ACD=60°.
又∵CF⊥AD,
∴∠FCD=∠ACD=30°,
∴在Rt△COE中,OE=OC,
∴OE=OB,
∴点E为OB的中点.
5.C 解析:如图,设圆心为O,过点O作OD⊥AB于点D,DO的延长线交☉O于点C,连接OA,
∵OD⊥AB于点D,DO的延长线交☉O于点C,
∴水的最大深度为CD=12 cm,AD=AB=×12=6(cm).
设OA=r cm,则OD=(12-r)cm,
在Rt△AOD中,OA2=OD2+AD2,即r2=(12-r)2+62,
解得r=7.5.
故该输水管的半径为7.5 cm.
故选C.
6. cm 解析:根据题意,得AB⊥OD,
∴AC=BC=AB=5 cm.
∵OB=OD,
∴OC=OD-CD=(OB-2)cm.
在Rt△BOC中,OB2=OC2+BC2,
∴OB2=(OB-2)2+52,
∴OB=,故☉O的半径OB长为 cm.
7.解:(1)如图,连接OB,
∵OC⊥AB,
∴D为AB的中点.
∵AB=7.2 m,
∴BD=AB=3.6 m.
又∵CD=2.4 m,
设OB=OC=r m,则OD=(r-2.4)m,
在Rt△BOD中,根据勾股定理得r2=(r-2.4)2+3.62,
解得r=3.9.
答:拱桥的半径为3.9 m.
(2)如图,连接OF,
∵OC⊥EF,
∴G为EF的中点.
∵EF=3 m,
∴GF=EF=1.5 m.
∵OF=3.9 m,
在Rt△OFG中,OG2=OF2-GF2=3.92-1.52=12.96,
∴OG==3.6(m),
∴CG=OC-OG=3.9-3.6=0.3(m)<1 m,
∴要禁止通行.
课后提升
1.D 解析:∵AB=10,
∴OA=OB=5,
∵OC∶OB=3∶5,
∴OC=3.
在Rt△OCD中,CD==4.
∵DE⊥AB,∴DE=2CD=8.
故选D.
2.C 解析:①当AB,CD在圆心两侧时,
过点O作OE⊥CD于点E,OF⊥AB于点F,连接OA,OC,如图,
∵半径r=5,弦AB∥CD,且AB=6,CD=8,
∴OA=OC=5,CE=DE=4,AF=FB=3.∵E,F,O在一条直线上,
∴EF为AB、CD之间的距离,
在Rt△OEC中,由勾股定理,得
OE2=OC2-CE2,
∴OE==3.
在Rt△OFA中,由勾股定理,得
OF2=OA2-AF2,
∴OF==4,
∴EF=OE+OF=3+4=7,
∴AB与CD的距离为7.
②当AB,CD在圆心同侧时(图略),
同①可得OE=3,OF=4,
则AB与CD的距离为OF-OE=1.
综上所述,AB与CD间的距离为1或7.
故选C.
3.7.5 解析:如图,设球心为O,过点O作OM⊥AD于点M,连接OA,
设球的半径为r cm,
由题意,得AD=12 cm,OM=32-20-r=(12-r)(cm).
由垂径定理,得AM=DM=AD=6 cm.
在Rt△OAM中,由勾股定理,得AM2+OM2=OA2,
即62+(12-r)2=r2,
解得r=7.5,
即球的半径为7.5 cm.
4.解:如图,连接OA,
设OA=r,则DG=r+1,
∵ED=EG,∴ED=,
∴OE=OD-ED=.
∵AB⊥CD于点E,AB=8,
∴AE=BE=4,
∴在Rt△OAE中,根据勾股定理,得OE2+AE2=OA2,
即2+42=r2,
解得r=(负值舍去),
即☉O的半径为.
5.解:(1)∵OC⊥AB,AB=80 mm,
∴AD=AB=40 mm.
(2)∵OC⊥AB,∴∠ADO=90°,
设半径OA=x mm,
则OC=OA=x mm,OD=OC-CD=(x-14)mm,
∴AD2+OD2=OA2,
即402+(x-14)2=x2,
解得x=64,
∴半径OA的长为64 mm.
6.解:(1)如图1,连接AO.
图1
∵CD⊥AB,CD经过圆心O,
∴AC=CB=0.9 m,
∴OC==1.2 m,
∴CD=OD+OC=1.5+1.2=2.7(m),
∴拱门最高点D到地面的距离为2.7 m.
(2)如图2,弦EF=2 m,且EF⊥CD,连接OE.
图2
∵CD⊥EF,CD经过圆心,
∴EJ=JF=1 m,
∴OJ=≈1.118(m),
∴CJ=1.2-1.118=0.082(m),
∵0.5>0.082,
∴搬运该桌子时能够通过拱门.
