3.8 圆内接正多边形课时作业(含答案) 2024-2025学年数学北师大版九年级下册
文档属性
| 名称 | 3.8 圆内接正多边形课时作业(含答案) 2024-2025学年数学北师大版九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 227.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-26 21:23:52 | ||
图片预览



文档简介
8 圆内接正多边形
圆内接正多边形的有关概念和计算
1.(2024扬州邗江区一模)如图,正五边形ABCDE内接于☉O,点P是劣弧BC上一点(点P不与点C重合),则∠CPD=( )
A.45° B.36° C.35° D.30°
2.如图,A,B,C,D为一个正多边形的顶点,O为正多边形的中心.若∠ADB=20°,则这个正多边形的边数为 ( )
A.7 B.8 C.9 D.10
3.如图,☉O与正五边形ABCDE的两边AE,CD相切于A,C两点,则∠AOC的度数是 ( )
A.108° B.129°
C.130° D.144°
4.如图,点O为正六边形ABCDEF的中心,则∠OAE的度数为 ( )
A.18° B.30° C.32° D.60°
5.若一个正多边形的每一个外角都是36°,则该正多边形的边数是 .
6.正十边形绕着它的中心至少旋转 ,能与它本身重合.
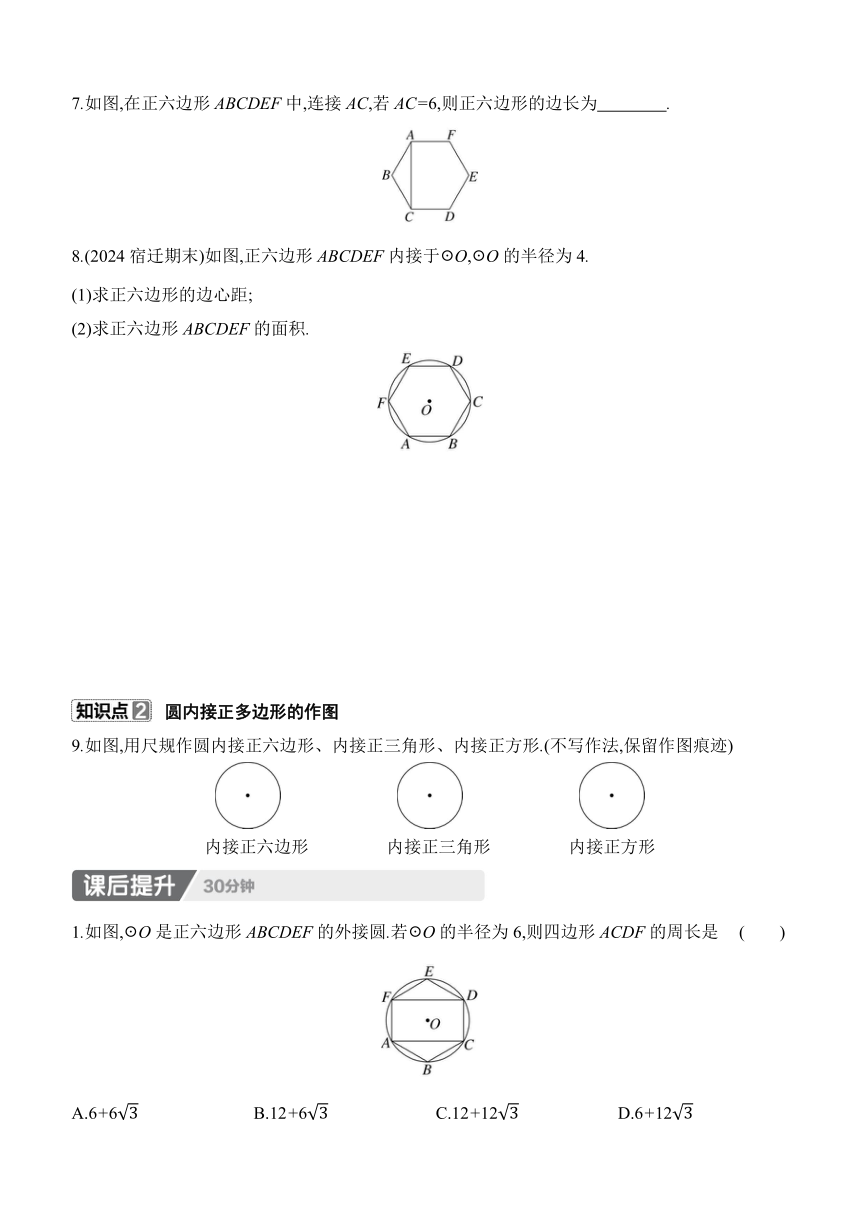
7.如图,在正六边形ABCDEF中,连接AC,若AC=6,则正六边形的边长为 .
8.(2024宿迁期末)如图,正六边形ABCDEF内接于☉O,☉O的半径为4.
(1)求正六边形的边心距;
(2)求正六边形ABCDEF的面积.
圆内接正多边形的作图
9.如图,用尺规作圆内接正六边形、内接正三角形、内接正方形.(不写作法,保留作图痕迹)
内接正六边形 内接正三角形 内接正方形
1.如图,☉O是正六边形ABCDEF的外接圆.若☉O的半径为6,则四边形ACDF的周长是 ( )
A.6+6 B.12+6 C.12+12 D.6+12
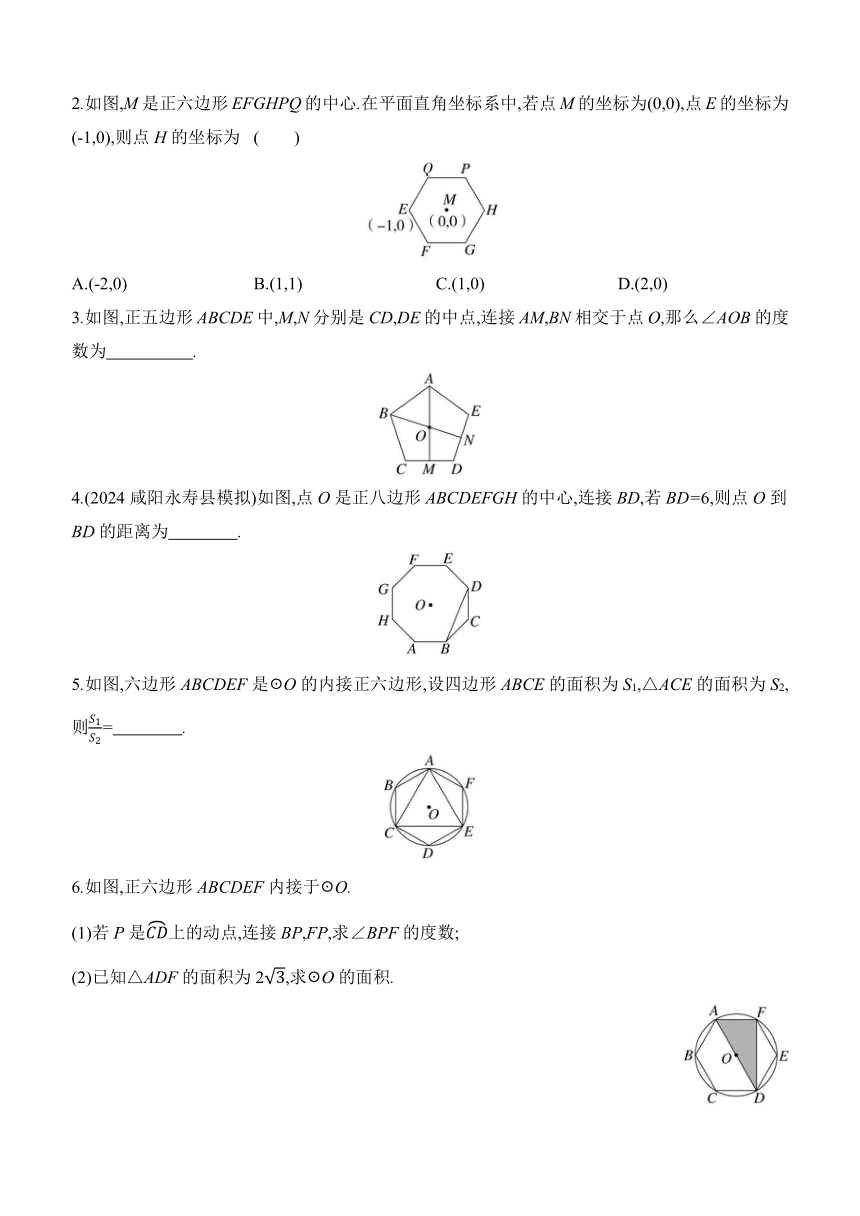
2.如图,M是正六边形EFGHPQ的中心.在平面直角坐标系中,若点M的坐标为(0,0),点E的坐标为(-1,0),则点H的坐标为 ( )
A.(-2,0) B.(1,1) C.(1,0) D.(2,0)
3.如图,正五边形ABCDE中,M,N分别是CD,DE的中点,连接AM,BN相交于点O,那么∠AOB的度数为 .
4.(2024咸阳永寿县模拟)如图,点O是正八边形ABCDEFGH的中心,连接BD,若BD=6,则点O到BD的距离为 .
5.如图,六边形ABCDEF是☉O的内接正六边形,设四边形ABCE的面积为S1,△ACE的面积为S2,则= .
6.如图,正六边形ABCDEF内接于☉O.
(1)若P是上的动点,连接BP,FP,求∠BPF的度数;
(2)已知△ADF的面积为2,求☉O的面积.
7.(几何直观)如图,☉O为△ABC的外接圆,半径长为5,∠BAC=∠BOC=120°.
(1)求BC的长.
(2)作∠BAC的平分线交☉O于点D.
①求证:△BDC为等边三角形;
②若AC=6,求AD的长.
【详解答案】
课堂达标
1.B 解析:如图,连接OC,OD,
∵五边形ABCDE是正五边形,
∴∠COD==72°,
∴∠CPD=∠COD=36°.
故选B.
2.C 解析:如图,连接OA,OB,
∵A,B,C,D为一个正多边形的顶点,O为正多边形的中心,
∴点A、B、C、D在以点O为圆心,OA为半径的同一个圆上,
∵∠ADB=20°,
∴∠AOB=2∠ADB=40°,
∴这个正多边形的边数==9.
故选C.
3.D 解析:∵五边形ABCDE是正五边形,
∴∠D=∠E==108°.
又∵☉O与正五边形ABCDE的两边AE,CD相切于A,C两点,
∴∠OAE=∠OCD=90°.
在五边形CDEAO中,
∠AOC=(5-2)×180°-90°×2-108°×2=144°,
故选D.
4.B 解析:如图,连接OF,
∵点O为正六边形ABCDEF的中心,
∴∠AOF=∠EOF=60°,
∴∠AOE=120°.
在等腰三角形AOE中,
∠OAE=×(180°-120°)=30°.
故选B.
5.10 解析:∵一个正多边形的每一个外角都是36°,
∴边数=360°÷36°=10.
6.36° 解析:∵360°÷10=36°,
∴该图形绕中心至少旋转36°后能与它本身重合.
7.2 解析:如图,连接BE,交AC于点H,
∵六边形ABCDEF是正六边形,
∴AB=BC,BE⊥AC,∠ABC=120°,
∴AH=CH=AC=3,∠AHB=90°,∠BAH=30°,
∴AB==2,
∴正六边形的边长为2.
8.解:(1)如图,连接OC,OD,过点O作OH⊥CD于点H,则∠OHC=∠OHD=90°.
∵六边形ABCDEF是正六边形,
∴∠COD=60°,∴△COD为等边三角形.
∴∠COH=30°,
∴=cos∠COH=cos 30°,∵OC=4,
∴圆心O到CD的距离OH=4×cos 30°=2,
即正六边形的边心距为2.
(2)由(1)得CD=OC=4,正六边形ABCDEF的面积=6S△COD=×4×2×6=24.
9.解:如图.
内接正六边形 内接正三角形 内接正方形
课后提升
1.C 解析:如图,连接OA,OF,OD,过点O作OM⊥DF于点M,则FM=DM=DF,
∵点O是正六边形ABCDEF的中心,
∴∠AOF==60°.
∵OA=OF,
∴△AOF是等边三角形,∴AF=OA=6.
在Rt△FOM中,∠OFM=90°-60°=30°,OF=6,
∴FM=OF=3,∴DF=2FM=6,
∴四边形ACDF的周长是2AF+2DF=12+12.
故选C.
2.C 解析:建立如图所示的平面直角坐标系,此时点M(0,0),点E(-1,0),
由正六边形的性质可知,点E、点M、点H都在x轴上,
且ME=MH=1,
∴点H(1,0).
故选C.
3.72° 解析:如图,连接BM,EM,BD,BE.
∵五边形ABCDE是正五边形,
∴BC=DE,∠BCM=∠EDM=108°.
∵M是CD的中点,
∴CM=DM,∴△BCM≌△EDM(SAS).
∴BM=EM.
∵AB=AE,∴AM垂直平分BE,
∴∠OBH+∠BOH=90°.
易证△BCD≌△BAE(SAS),
∴BD=BE.
∵N是DE的中点,∴BN⊥DE,
∴∠EBN+∠BEN=90°,
∴∠BOH=∠BEN.
∵∠BAE=108°,AB=AE,
∴∠AEB=∠ABE=36°,
∴∠BEN=108°-36°=72°,
∴∠BOA=∠BEN=72°.
4.3 解析:如图,连接OB,OC,OD,OC与BD相交于点M,
∵八边形ABCDEFGH是正八边形,
∴∠BOC=∠COD==45°,
∴∠BOD=45°+45°=90°.
∵OB=OD,∠BOC=∠COD=45°,
∴OC⊥BD,
∴OM=BM=DM=BD=3,
即点O到BD的距离为3.
5. 解析:如图,连接OA,OB,OC,OE,
∵六边形ABCDEF是☉O的内接正六边形,
∴OA=OC=OE,
∠AOC=∠COE=∠AOE=2∠AOB=2∠BOC=2×=120°,
∴△AOC≌△COE≌△AOE(SAS),
∴S△AOC=S△COE=S△AOE.
∵OA=OB=OC,∠AOB=∠BOC=60°,
∴△AOB,△BOC都是等边三角形,
∴OA=OB=AB=OC=BC,
即OA=BA,OC=BC,
又∵AC=AC,
∴△ABC≌△AOC(SSS),
∴S△ABC=S△AOC,
∴S△ABC=S△AOC=S△COE=S△AOE,
即S1=4S△AOC,S2=3S△AOC,
∴.
6.解:(1)如图,连接AP,FO,
∵六边形ABCDEF是正六边形,
∴AF=AB,∠AOF==60°,
∴∠APF=∠AOF=30°.
∵AF=AB,
∴∠APB=∠APF=30°,
∴∠BPF=∠APB+∠APF=60°.
(2)∵∠AOF=60°,AO=FO,
∴△AOF是等边三角形,
∴∠DAF=60°.
∵AD为☉O的直径,
∴∠AFD=90°,
∴DF=AF,
∴S△ADF=AF×DF=AF2=2,
∴AF=2,∴☉O的半径为2,
∴☉O的面积=π×22=4π.
7.解:(1)如图,过点O作OM⊥BC,垂足为M,则BM=CM=BC.
∵OB=OC,∠BOC=120°,
∴∠BOM=∠BOC=60°.
在Rt△BOM中,∠BOM=60°,OB=5,
∴BM=OB=,
∴BC=2BM=15.
(2)①证明:∵AD平分∠BAC,
∠BAC=120°,
∴∠BAD=∠CAD=∠BAC=60°,
∴∠DBC=∠CAD=60°,∠BCD=∠BAD=60°,
∴∠BCD=∠CDB=∠DBC=60°,
∴△BDC为等边三角形.
②如图,过点C作CN⊥AD,垂足为N,
在Rt△ANC中,∠CAN=60°,AC=6,
∴AN=AC=3,CN=AC=9.
在Rt△CDN中,CN=9,CD=BC=15,由勾股定理,得
DN==12,
∴AD=AN+DN=12+3.
圆内接正多边形的有关概念和计算
1.(2024扬州邗江区一模)如图,正五边形ABCDE内接于☉O,点P是劣弧BC上一点(点P不与点C重合),则∠CPD=( )
A.45° B.36° C.35° D.30°
2.如图,A,B,C,D为一个正多边形的顶点,O为正多边形的中心.若∠ADB=20°,则这个正多边形的边数为 ( )
A.7 B.8 C.9 D.10
3.如图,☉O与正五边形ABCDE的两边AE,CD相切于A,C两点,则∠AOC的度数是 ( )
A.108° B.129°
C.130° D.144°
4.如图,点O为正六边形ABCDEF的中心,则∠OAE的度数为 ( )
A.18° B.30° C.32° D.60°
5.若一个正多边形的每一个外角都是36°,则该正多边形的边数是 .
6.正十边形绕着它的中心至少旋转 ,能与它本身重合.
7.如图,在正六边形ABCDEF中,连接AC,若AC=6,则正六边形的边长为 .
8.(2024宿迁期末)如图,正六边形ABCDEF内接于☉O,☉O的半径为4.
(1)求正六边形的边心距;
(2)求正六边形ABCDEF的面积.
圆内接正多边形的作图
9.如图,用尺规作圆内接正六边形、内接正三角形、内接正方形.(不写作法,保留作图痕迹)
内接正六边形 内接正三角形 内接正方形
1.如图,☉O是正六边形ABCDEF的外接圆.若☉O的半径为6,则四边形ACDF的周长是 ( )
A.6+6 B.12+6 C.12+12 D.6+12
2.如图,M是正六边形EFGHPQ的中心.在平面直角坐标系中,若点M的坐标为(0,0),点E的坐标为(-1,0),则点H的坐标为 ( )
A.(-2,0) B.(1,1) C.(1,0) D.(2,0)
3.如图,正五边形ABCDE中,M,N分别是CD,DE的中点,连接AM,BN相交于点O,那么∠AOB的度数为 .
4.(2024咸阳永寿县模拟)如图,点O是正八边形ABCDEFGH的中心,连接BD,若BD=6,则点O到BD的距离为 .
5.如图,六边形ABCDEF是☉O的内接正六边形,设四边形ABCE的面积为S1,△ACE的面积为S2,则= .
6.如图,正六边形ABCDEF内接于☉O.
(1)若P是上的动点,连接BP,FP,求∠BPF的度数;
(2)已知△ADF的面积为2,求☉O的面积.
7.(几何直观)如图,☉O为△ABC的外接圆,半径长为5,∠BAC=∠BOC=120°.
(1)求BC的长.
(2)作∠BAC的平分线交☉O于点D.
①求证:△BDC为等边三角形;
②若AC=6,求AD的长.
【详解答案】
课堂达标
1.B 解析:如图,连接OC,OD,
∵五边形ABCDE是正五边形,
∴∠COD==72°,
∴∠CPD=∠COD=36°.
故选B.
2.C 解析:如图,连接OA,OB,
∵A,B,C,D为一个正多边形的顶点,O为正多边形的中心,
∴点A、B、C、D在以点O为圆心,OA为半径的同一个圆上,
∵∠ADB=20°,
∴∠AOB=2∠ADB=40°,
∴这个正多边形的边数==9.
故选C.
3.D 解析:∵五边形ABCDE是正五边形,
∴∠D=∠E==108°.
又∵☉O与正五边形ABCDE的两边AE,CD相切于A,C两点,
∴∠OAE=∠OCD=90°.
在五边形CDEAO中,
∠AOC=(5-2)×180°-90°×2-108°×2=144°,
故选D.
4.B 解析:如图,连接OF,
∵点O为正六边形ABCDEF的中心,
∴∠AOF=∠EOF=60°,
∴∠AOE=120°.
在等腰三角形AOE中,
∠OAE=×(180°-120°)=30°.
故选B.
5.10 解析:∵一个正多边形的每一个外角都是36°,
∴边数=360°÷36°=10.
6.36° 解析:∵360°÷10=36°,
∴该图形绕中心至少旋转36°后能与它本身重合.
7.2 解析:如图,连接BE,交AC于点H,
∵六边形ABCDEF是正六边形,
∴AB=BC,BE⊥AC,∠ABC=120°,
∴AH=CH=AC=3,∠AHB=90°,∠BAH=30°,
∴AB==2,
∴正六边形的边长为2.
8.解:(1)如图,连接OC,OD,过点O作OH⊥CD于点H,则∠OHC=∠OHD=90°.
∵六边形ABCDEF是正六边形,
∴∠COD=60°,∴△COD为等边三角形.
∴∠COH=30°,
∴=cos∠COH=cos 30°,∵OC=4,
∴圆心O到CD的距离OH=4×cos 30°=2,
即正六边形的边心距为2.
(2)由(1)得CD=OC=4,正六边形ABCDEF的面积=6S△COD=×4×2×6=24.
9.解:如图.
内接正六边形 内接正三角形 内接正方形
课后提升
1.C 解析:如图,连接OA,OF,OD,过点O作OM⊥DF于点M,则FM=DM=DF,
∵点O是正六边形ABCDEF的中心,
∴∠AOF==60°.
∵OA=OF,
∴△AOF是等边三角形,∴AF=OA=6.
在Rt△FOM中,∠OFM=90°-60°=30°,OF=6,
∴FM=OF=3,∴DF=2FM=6,
∴四边形ACDF的周长是2AF+2DF=12+12.
故选C.
2.C 解析:建立如图所示的平面直角坐标系,此时点M(0,0),点E(-1,0),
由正六边形的性质可知,点E、点M、点H都在x轴上,
且ME=MH=1,
∴点H(1,0).
故选C.
3.72° 解析:如图,连接BM,EM,BD,BE.
∵五边形ABCDE是正五边形,
∴BC=DE,∠BCM=∠EDM=108°.
∵M是CD的中点,
∴CM=DM,∴△BCM≌△EDM(SAS).
∴BM=EM.
∵AB=AE,∴AM垂直平分BE,
∴∠OBH+∠BOH=90°.
易证△BCD≌△BAE(SAS),
∴BD=BE.
∵N是DE的中点,∴BN⊥DE,
∴∠EBN+∠BEN=90°,
∴∠BOH=∠BEN.
∵∠BAE=108°,AB=AE,
∴∠AEB=∠ABE=36°,
∴∠BEN=108°-36°=72°,
∴∠BOA=∠BEN=72°.
4.3 解析:如图,连接OB,OC,OD,OC与BD相交于点M,
∵八边形ABCDEFGH是正八边形,
∴∠BOC=∠COD==45°,
∴∠BOD=45°+45°=90°.
∵OB=OD,∠BOC=∠COD=45°,
∴OC⊥BD,
∴OM=BM=DM=BD=3,
即点O到BD的距离为3.
5. 解析:如图,连接OA,OB,OC,OE,
∵六边形ABCDEF是☉O的内接正六边形,
∴OA=OC=OE,
∠AOC=∠COE=∠AOE=2∠AOB=2∠BOC=2×=120°,
∴△AOC≌△COE≌△AOE(SAS),
∴S△AOC=S△COE=S△AOE.
∵OA=OB=OC,∠AOB=∠BOC=60°,
∴△AOB,△BOC都是等边三角形,
∴OA=OB=AB=OC=BC,
即OA=BA,OC=BC,
又∵AC=AC,
∴△ABC≌△AOC(SSS),
∴S△ABC=S△AOC,
∴S△ABC=S△AOC=S△COE=S△AOE,
即S1=4S△AOC,S2=3S△AOC,
∴.
6.解:(1)如图,连接AP,FO,
∵六边形ABCDEF是正六边形,
∴AF=AB,∠AOF==60°,
∴∠APF=∠AOF=30°.
∵AF=AB,
∴∠APB=∠APF=30°,
∴∠BPF=∠APB+∠APF=60°.
(2)∵∠AOF=60°,AO=FO,
∴△AOF是等边三角形,
∴∠DAF=60°.
∵AD为☉O的直径,
∴∠AFD=90°,
∴DF=AF,
∴S△ADF=AF×DF=AF2=2,
∴AF=2,∴☉O的半径为2,
∴☉O的面积=π×22=4π.
7.解:(1)如图,过点O作OM⊥BC,垂足为M,则BM=CM=BC.
∵OB=OC,∠BOC=120°,
∴∠BOM=∠BOC=60°.
在Rt△BOM中,∠BOM=60°,OB=5,
∴BM=OB=,
∴BC=2BM=15.
(2)①证明:∵AD平分∠BAC,
∠BAC=120°,
∴∠BAD=∠CAD=∠BAC=60°,
∴∠DBC=∠CAD=60°,∠BCD=∠BAD=60°,
∴∠BCD=∠CDB=∠DBC=60°,
∴△BDC为等边三角形.
②如图,过点C作CN⊥AD,垂足为N,
在Rt△ANC中,∠CAN=60°,AC=6,
∴AN=AC=3,CN=AC=9.
在Rt△CDN中,CN=9,CD=BC=15,由勾股定理,得
DN==12,
∴AD=AN+DN=12+3.
