第二章 二次函数 单元评估测试卷(含详解)2024-2025学年数学北师大版九年级下册
文档属性
| 名称 | 第二章 二次函数 单元评估测试卷(含详解)2024-2025学年数学北师大版九年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 294.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-26 21:27:07 | ||
图片预览




文档简介
第二章 二次函数 评估测试卷
(满分:120分 时间:120分钟)
一、选择题(本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列函数中,y关于x的二次函数是 ( )
A.y=ax2+bx+c B.y=x(x-1)
C.y= D.y=(x-1)2-x2
2.(2024南宁青秀区期末)如图,二次函数y=-x2+mx+n的图象与x轴的一个交点坐标为(5,0),那么关于x的一元二次方程-x2+mx+n=0的解为 ( )
A.x1=5,x2=1 B.x1=5,x2=-1
C.x1=5,x2=-5 D.x=5
3.(2024凉山州中考)抛物线y=(x-1)2+c经过(-2,y1),(0,y2),,y3三点,则y1,y2,y3的大小关系正确的是 ( )
A.y1>y2>y3
B.y2>y3>y1
C.y3>y1>y2
D.y1>y3>y2
4.下列抛物线中,对称轴为直线x=1的抛物线的表达式是 ( )
A.y=x2+1 B.y=x2-1
C.y=x2+2x D.y=x2-2x
5.某厂今年一月份新产品的研发资金为10万元,以后每月新产品的研发资金与上月相比增长率都是x,则该厂今年一季度新产品的研发资金y(元)关于x的函数关系式为 ( )
A.y=10(1+x)3
B.y=10+10(1+x)+10(1+x)2
C.y=10+10x+x2
D.y=10(1+x)2
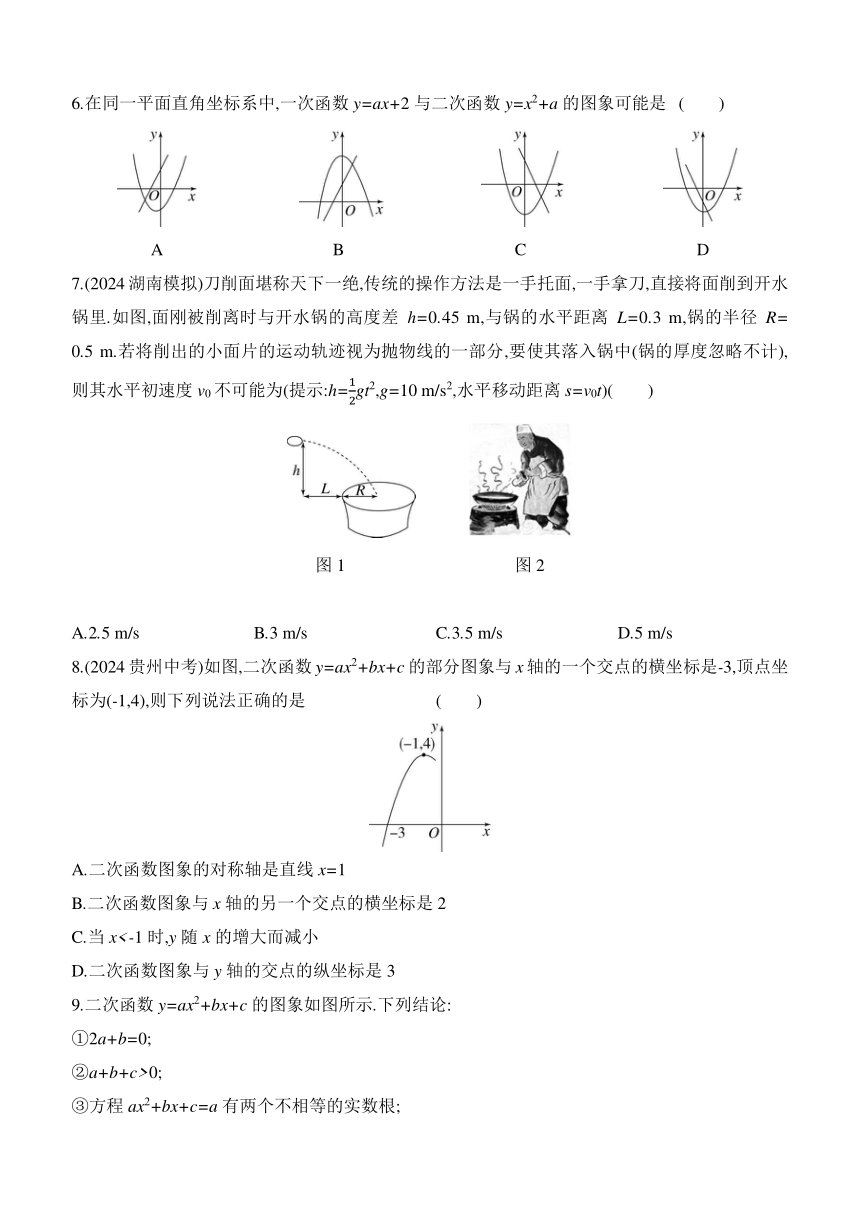
6.在同一平面直角坐标系中,一次函数y=ax+2与二次函数y=x2+a的图象可能是 ( )
A B C D
7.(2024湖南模拟)刀削面堪称天下一绝,传统的操作方法是一手托面,一手拿刀,直接将面削到开水锅里.如图,面刚被削离时与开水锅的高度差h=0.45 m,与锅的水平距离L=0.3 m,锅的半径R=
0.5 m.若将削出的小面片的运动轨迹视为抛物线的一部分,要使其落入锅中(锅的厚度忽略不计),则其水平初速度v0不可能为(提示:h=gt2,g=10 m/s2,水平移动距离s=v0t)( )
图1 图2
A.2.5 m/s B.3 m/s C.3.5 m/s D.5 m/s
8.(2024贵州中考)如图,二次函数y=ax2+bx+c的部分图象与x轴的一个交点的横坐标是-3,顶点坐标为(-1,4),则下列说法正确的是 ( )
A.二次函数图象的对称轴是直线x=1
B.二次函数图象与x轴的另一个交点的横坐标是2
C.当x<-1时,y随x的增大而减小
D.二次函数图象与y轴的交点的纵坐标是3
9.二次函数y=ax2+bx+c的图象如图所示.下列结论:
①2a+b=0;
②a+b+c>0;
③方程ax2+bx+c=a有两个不相等的实数根;
④不等式ax2+bx+c<0的解集是0其中所有正确结论的序号是 ( )
A.①③ B.②④ C.①③④ D.①②③④
10.(2024天津中考)从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是h=30t-5t2(0≤t≤6).有下列结论:
①小球从抛出到落地需要6 s;
②小球运动中的高度可以是30 m;
③小球运动2 s时的高度小于运动5 s时的高度.
其中,正确结论的个数是 ( )
A.0 B.1 C.2 D.3
二、填空题(本题共5小题,每小题3分,共15分)
11.(2024滨州中考)将抛物线y=-x2先向右平移1个单位长度,再向上平移2个单位长度,则平移后抛物线的顶点坐标为 .
12.已知一条抛物线的形状、开口方向均与抛物线y=-2x2+9x相同,且它的顶点坐标为(-1,6),则这条抛物线的表达式为 .
13.关于x的二次函数y=ax2-4ax+b中,当1≤x≤4时,-3≤y≤5.则b-4a的值为 .
14.如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴相交于点A,B,点B的坐标为(3,0),若点C(2,3)在抛物线上,则AB的长为 .
15.九(1)班劳动实践基地内有一块面积足够大的平整空地,地上两段围墙AB⊥CD于点O(如图),其中AB上的EO段围墙空缺.同学们测得AE=6.6 m,OE=1.4 m,OB=6 m,OC=5 m,OD=3 m,班长买来可切断的围栏16 m,准备利用已有围墙,围出一块封闭的矩形菜地,则该菜地最大面积是
m2.
三、解答题(本题共8小题,共75分.解答应写出文字说明、演算步骤或推理过程)
16.(8分)已知二次函数y=x2-4x+3.
(1)求二次函数y=x2-4x+3图象的顶点坐标;
(2)在平面直角坐标系中,画出二次函数y=x2-4x+3的图象;
(3)当117.(8分)二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象回答下列问题:
(1)求点B的坐标;
(2)当x 时,y随x的增大而减小;
(3)不等式ax2+bx+c>0的解集是什么
18.(8分)(2024济宁中考)某商场以每件80元的价格购进一种商品,在一段时间内,销售量y(单位:件)与销售单价x(单位:元/件)之间是一次函数关系,其部分图象如图所示.
(1)求这段时间内y与x之间的函数表达式;
(2)在这段时间内,若销售单价不低于100元,且商场还要完成不少于220件的销售任务,当销售单价为多少时,商场获得利润最大 最大利润是多少
19.(8分)已知二次函数y=2x2-mx-m2.
(1)求证:对于任意实数m,二次函数y=2x2-mx-m2的图象与x轴总有交点.
(2)若这个二次函数的图象与x轴交于点A,B(1,0),求点A的坐标.
20.(8分)如图,抛物线y=-x2+2x+c经过坐标原点O和点A,点A在x轴上.
(1)求此抛物线的表达式,并求出顶点B的坐标;
(2)连接OB,AB,求S△OAB;
(3)若点C在抛物线上,且S△OAC=8,求点C的坐标.
21.(10分)已知抛物线y=-x2+bx(b为常数)的顶点横坐标比抛物线y=-x2+2x的顶点横坐标大1.
(1)求b的值;
(2)点A(x1,y1)在抛物线y=-x2+2x上,点B(x1+t,y1+h)在抛物线y=-x2+bx上.
①若h=3t,且x1≥0,t>0,求h的值;
②若x1=t-1,求h的最大值.
22.(12分)(2024浙江中考)已知二次函数y=x2+bx+c(b,c为常数)的图象经过点A(-2,5),对称轴为直线x=-.
(1)求二次函数的表达式;
(2)若点B(1,7)向上平移2个单位长度,向左平移m(m>0)个单位长度后,恰好落在y=x2+bx+c的图象上,求m的值;
(3)当-2≤x≤n时,二次函数y=x2+bx+c的最大值与最小值的差为,求n的取值范围.
23.(13分)(2024辽宁中考)已知y1是自变量x的函数,当y2=xy1时,称函数y2为函数y1的“升幂函数”.在平面直角坐标系中,对于函数y1图象上任意一点A(m,n),称点B(m,mn)为点A“关于y1的升幂点”,点B在函数y1的“升幂函数”y2的图象上.
例如:函数y1=2x,当y2=xy1=x·2x=2x2时,则函数y2=2x2是函数y1=2x的“升幂函数”.在平面直角坐标系中,函数y1=2x的图象上任意一点A(m,2m),点B(m,2m2)为点A“关于y1的升幂点”,点B在函数y1=2x的“升幂函数”y2=2x2的图象上.
(1)求函数y1=x的“升幂函数”y2的函数表达式;
(2)如图,点A在函数y1=x>0的图象上,点A“关于y1的升幂点”B在点A上方,当AB=2时,求点A的坐标;
(3)点A在函数y1=-x+4的图象上,点A“关于y1的升幂点”为点B,设点A的横坐标为m.
①若点B与点A重合,求m的值;
②若点B在点A的上方,过点B作x轴的平行线,与函数y1的“升幂函数”y2的图象相交于点C,以AB,BC为邻边构造矩形ABCD,设矩形ABCD的周长为y,求y关于m的函数表达式;
③在②的条件下,当直线y=t1与函数y的图象的交点有3个时,从左到右依次记为E,F,G,当直线y=t2与函数y的图象的交点有2个时,从左到右依次记为M,N,若EF=MN,请直接写出t2-t1的值.
备用图
【详解答案】
1.B 解析:A.当a=0时,y=bx+c不是二次函数;B.y=x(x-1)=x2-x是二次函数;C.y=不是二次函数;D.y=(x-1)2-x2=
-2x+1为一次函数.故选B.
2.B 解析:由题意,根据函数的图象可得,二次函数y=-x2+mx+n的图象的对称轴是直线x=2,又图象与x轴的一个交点坐标为(5,0),∴图象与x轴的另一个交点坐标为(2-3,0),即(-1,0).∴关于x的一元二次方程-x2+mx+n=0的解为x1=5,x2=-1.故选B.
3.D 解析:∵y=(x-1)2+c,∴抛物线开口向上,对称轴是直线x=1,∴当x<1时,y随x的增大而减小,∵,y3关于直线x=1的对称点是-,y3,-2<-<0<1,∴y1>y3>y2.故选D.
4.D 解析:∵抛物线y=x2+1的对称轴为y轴,∴选项A不符合题意;∵抛物线y=x2-1的对称轴为y轴,∴选项B不符合题意;∵抛物线y=x2+2x=(x+1)2-1,∴该抛物线的对称轴为直线x=-1,∴选项C不符合题意;∵抛物线y=x2-2x=(x-1)2-1,∴该抛物线的对称轴为直线x=1,∴选项D符合题意.故选D.
5.B 解析:∵该厂今年一月份新产品的研发资金为10万元,以后每月新产品的研发资金与上月相比增长率都是x,∴该厂今年二月份新产品的研发资金为10(1+x)万元,三月份新产品的研发资金为10(1+x)2万元.根据题意得:y=10+10(1+x)+10(1+x)2.故选B.
6.C 解析:∵二次函数y=x2+a,∴抛物线开口向上,∴排除B,∵一次函数y=ax+2,∴直线与y轴的正半轴相交,
∴排除D;∵由抛物线得a<0,∴排除A;故选C.
7.D 解析:∵h=gt2,∴t==0.3(s),∵L8.D 解析:选项A:∵顶点坐标为(-1,4),∴对称轴为直线x=-1,故选项A错误;选项B:由对称性可知,(-3,0)关于x=-1对称的点为(1,0),故选项B错误;选项C:开口向下,当x<-1时,y随x的增大而增大,故选项C错误;选项D:设二次函数表达式为y=a(x+1)2+4,将(-3,0)代入得a=-1,∴y=-(x+1)2+4,令x=0得y=3,∴二次函数图象与y轴的交点的纵坐标是3,故选项D正确.故选D.
9.A 解析:由图象得:a>0,与x轴相交于点(-1,0)和(3,0),∴抛物线的对称轴为直线x==1,即-=1,∴b+2a=0,故①是正确的;由图象得:当x=1时,y<0,即a+b+c<0,故②是错误的;∵a>0,∴y=a在x轴的上方,∴y=ax2+bx+c的图象与y=a有两个交点,故③是正确的;y=ax2+bx+c的图象与x轴的交点为(-1,0),(3,0),∴不等式ax2+bx+c<0的解集是-110.C 解析:①令h=0,则30t-5t2=0,解得t1=0,t2=6,∴小球从抛出到落地需要6 s,故①正确;②h=30t-5t2=-5(t2-6t)=
-5(t-3)2+45,∵-5<0,∴当t=3时,h有最大值,最大值为45,∴小球运动中的高度可以是30 m,故②正确;③t=2时,h=30×2-5×4=40(m),t=5时,h=30×5-5×25=25(m),∴小球运动2 s时的高度大于运动5 s时的高度,故③错误.故选C.
11.(1,2) 解析:将抛物线y=-x2先向右平移1个单位长度,再向上平移2个单位长度后抛物线表达式为y=-(x-1)2+2,∴顶点坐标为(1,2).
12.y=-2(x+1)2+6 解析:∵抛物线的顶点坐标为(-1,6),∴抛物线表达式可设为y=a(x+1)2+6,∵抛物线y=a(x+1)2+6的形状、开口方向均与抛物线y=-2x2+9x相同,∴a=-2,∴所求抛物线的表达式为y=-2(x+1)2+6.
13.-3或5 解析:∵抛物线y=ax2-4ax+b=a(x-2)2+b-4a,∴顶点为(2,b-4a),当a>0时,当1≤x≤4时,-3≤y≤5,函数有最小值,∴b-4a=-3,当a<0时,当1≤x≤4时,-3≤y≤5,函数有最大值,∴b-4a=5,故b-4a的值为-3或5.
14.4 解析:∵抛物线y=ax2+bx+3过B(3,0),C(2,3),
∴∴抛物线为y=-x2+2x+3.∴抛物线的对称轴是直线x=-=1.∵抛物线与x轴的一交点为B(3,0),∴另一交点为A(1-2,0),即A(-1,0).∴AB=3-(-1)=4.
15.46.4 解析:设矩形在射线OA上的一段长为x m.
(1)当x≤8时,S=x·=-x2+9.8x=-(x-9.8)2+48.02,当x=8时,S=46.4,
(2)当x>8时,S=x·-x=-x2+13.8x=-(x-6.9)2+47.61,由于在x>8的范围内,S均小于46.4.所以由(1)(2)得最大面积为46.4 m2.
16.解:(1)∵y=x2-4x+3=(x-2)2-1,
∴该二次函数图象顶点坐标为(2,-1).
(2)当y=0时,x2-4x+3=0,解得x1=1,x2=3,
∴抛物线与x轴的交点坐标为(1,0),(3,0);
当x=0时,y=x2-4x+3=3,则抛物线与y轴的交点坐标为(0,3),关于对称轴的对称点为(4,3),
如图.
(3)由图象可知,当117.解:(1)由图象可知,A,B到直线x=1的距离相等,
∵A(-1,0),
∴点B坐标为(3,0).
(2)>1
(3)由图象可知,不等式ax2+bx+c>0的解集是-118.解:(1)由题意,设一次函数的表达式为y=kx+b,
又过(100,300),(120,200),
∴
∴
∴这段时间内y与x之间函数表达式为y=-5x+800.
(2)由题意得,
∴100≤x≤116.
∵商场获得的利润=(x-80)(-5x+800)
=-5x2+1 200x-64 000
=-5(x-120)2+8 000,
又-5<0,100≤x≤116,
∴当x=116时,利润最大,最大值为7 920.
答:当销售单价为116元/件时,商场获得利润最大,最大利润是7 920元.
19.解:(1)证明:∵Δ=(-m)2-4×2×(-m2)=9m2≥0,
∴对于任意实数m,二次函数y=2x2-mx-m2的图象与x轴总有交点.
(2)把B(1,0)代入y=2x2-mx-m2得2-m-m2=0,解得m1=-2,m2=1,
当m=-2时,抛物线表达式为y=2x2+2x-4,解方程2x2+2x-4=0,解得x1=-2,x2=1,此时点A坐标为(-2,0);
当m=1时,抛物线表达式为y=2x2-x-1,解方程2x2-x-1=0,解得x1=-,x2=1,此时A点坐标为-,0.
综上所述,A点坐标为(-2,0)或-,0.
20.解:(1)把(0,0)代入y=-x2+2x+c得c=0,
∴抛物线表达式为y=-x2+2x,
∴y=-x2+2x=-(x-1)2+1,
∴顶点B的坐标为(1,1).
(2)当y=0时,-x2+2x=0,
解得x1=0,x2=2,
∴A(2,0),
∴S△OAB=×2×1=1.
(3)设点C坐标为(t,-t2+2t),
∵S△OAC=8,
∴×2×|-t2+2t|=8,
即t2-2t=8或t2-2t=-8,
解方程t2-2t=8得t1=-2,t2=4,
∴点C坐标为(-2,-8)或(4,-8),
方程t2-2t=-8无实数解,
综上所述,点C坐标为(-2,-8)或(4,-8).
21.解:(1)∵抛物线y=-x2+bx的顶点横坐标为,y=-x2+2x的顶点横坐标为1,
∴-1=1,
∴b=4.
(2)∵点A(x1,y1)在抛物线y=-x2+2x上,
∴y1=-+2x1,
∵点B(x1+t,y1+h)在抛物线y=-x2+4x上,
∴y1+h=-(x1+t)2+4(x1+t),
-+2x1+h=-+4(x1+t),
∴h=-t2-2x1t+2x1+4t,
①∵h=3t,
∴3t=-t2-2x1t+2x1+4t,
∴t(t+2x1)=t+2x1,
∵x1≥0,t>0,
∴t+2x1>0,
∴t=1,
∴h=3.
②将x1=t-1代入h=-t2-2x1t+2x1+4t,
∴h=-3t2+8t-2,
h=-3,
∵-3<0,
∴当t=,即x1=时,h取最大值.
22.解:(1)∵二次函数为y=x2+bx+c,
∴抛物线的对称轴为直线x=-=-.
∴b=1.
∴抛物线为y=x2+x+c.
又∵图象经过点A(-2,5),
∴4-2+c=5.
∴c=3.
∴抛物线为y=x2+x+3.
(2)∵点B(1,7)向上平移2个单位长度,向左平移m个单位长度(m>0),
∴平移后的点为(1-m,9).
又∵(1-m,9)在y=x2+x+3上,
∴9=(1-m)2+(1-m)+3.
∴m=4或m=-1(舍去).
∴m=4.
(3)由题意,当n<-时,
∴最大值与最小值的差为5-=.
∴n1=n2=-,不符合题意,舍去.
当-≤n≤1时,
∴最大值与最小值的差为5-,符合题意.
当n>1时,最大值与最小值的差为-,解得n1=1或n2=-2,不符合题意.
综上所述,n的取值范围为-≤n≤1.
23.解:(1)y2=xy1=x×x=x2.
(2)如图1,
图1
∵y2=xy1=x×=3,
设Am,,B(m,3),
∵点B在点A的上方,
∴当AB=2时,3-=2,
解得m=3.
∴A(3,1).
(3)①∵y2=xy1=x(-x+4)=-x2+4x,
∴A(m,-m+4),B(m,-m2+4m).
如果点B与点A重合,那么-m+4=-m2+4m.
整理,得m2-5m+4=0.
解得m=1或m=4.
②由①可知,直线y=-x+4与抛物线y=-x2+4x有两个交点(1,3)和(4,0),
如图2所示,函数y2=-x2+4x的图象是开口向下的抛物线,对称轴是直线x=2.
图2
∵BC∥x轴,∴B,C两点关于直线x=2对称.
如图2,当点B在点C右侧时,2如图3,当点B在点C左侧时,1由点B在点A的上方,得BA=(-m2+4m)-(-m+4)=-m2+5m-4,
当2当1综上,y=
图3
③t2-t1=4或3-2.
解析:情形1:如图4,如果EF和MN平行且相等,那这两条平行线间的距离等于两个顶点之间的竖直高度,或者等于P,Q两点间的竖直高度.
当m=2时,y=-2m2+6m=4,
∴P(2,4).
当m=4时,y=-2m2+14m-16=8,
∴Q(4,8).
∴t2-t1=8-4=4.
图4
情形2,如图5(图4局部,变形处理),点M是抛物线y=-2m2+6m的顶点.
由M,,得N,,
∴MN=EF=-=2-,
∴点F的横坐标xF=,
于是可得yF=,
∴t2-t1=yN-yF=-=3-2.
图5
综上,t2-t1=4或3-2.
(满分:120分 时间:120分钟)
一、选择题(本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列函数中,y关于x的二次函数是 ( )
A.y=ax2+bx+c B.y=x(x-1)
C.y= D.y=(x-1)2-x2
2.(2024南宁青秀区期末)如图,二次函数y=-x2+mx+n的图象与x轴的一个交点坐标为(5,0),那么关于x的一元二次方程-x2+mx+n=0的解为 ( )
A.x1=5,x2=1 B.x1=5,x2=-1
C.x1=5,x2=-5 D.x=5
3.(2024凉山州中考)抛物线y=(x-1)2+c经过(-2,y1),(0,y2),,y3三点,则y1,y2,y3的大小关系正确的是 ( )
A.y1>y2>y3
B.y2>y3>y1
C.y3>y1>y2
D.y1>y3>y2
4.下列抛物线中,对称轴为直线x=1的抛物线的表达式是 ( )
A.y=x2+1 B.y=x2-1
C.y=x2+2x D.y=x2-2x
5.某厂今年一月份新产品的研发资金为10万元,以后每月新产品的研发资金与上月相比增长率都是x,则该厂今年一季度新产品的研发资金y(元)关于x的函数关系式为 ( )
A.y=10(1+x)3
B.y=10+10(1+x)+10(1+x)2
C.y=10+10x+x2
D.y=10(1+x)2
6.在同一平面直角坐标系中,一次函数y=ax+2与二次函数y=x2+a的图象可能是 ( )
A B C D
7.(2024湖南模拟)刀削面堪称天下一绝,传统的操作方法是一手托面,一手拿刀,直接将面削到开水锅里.如图,面刚被削离时与开水锅的高度差h=0.45 m,与锅的水平距离L=0.3 m,锅的半径R=
0.5 m.若将削出的小面片的运动轨迹视为抛物线的一部分,要使其落入锅中(锅的厚度忽略不计),则其水平初速度v0不可能为(提示:h=gt2,g=10 m/s2,水平移动距离s=v0t)( )
图1 图2
A.2.5 m/s B.3 m/s C.3.5 m/s D.5 m/s
8.(2024贵州中考)如图,二次函数y=ax2+bx+c的部分图象与x轴的一个交点的横坐标是-3,顶点坐标为(-1,4),则下列说法正确的是 ( )
A.二次函数图象的对称轴是直线x=1
B.二次函数图象与x轴的另一个交点的横坐标是2
C.当x<-1时,y随x的增大而减小
D.二次函数图象与y轴的交点的纵坐标是3
9.二次函数y=ax2+bx+c的图象如图所示.下列结论:
①2a+b=0;
②a+b+c>0;
③方程ax2+bx+c=a有两个不相等的实数根;
④不等式ax2+bx+c<0的解集是0
A.①③ B.②④ C.①③④ D.①②③④
10.(2024天津中考)从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)之间的关系式是h=30t-5t2(0≤t≤6).有下列结论:
①小球从抛出到落地需要6 s;
②小球运动中的高度可以是30 m;
③小球运动2 s时的高度小于运动5 s时的高度.
其中,正确结论的个数是 ( )
A.0 B.1 C.2 D.3
二、填空题(本题共5小题,每小题3分,共15分)
11.(2024滨州中考)将抛物线y=-x2先向右平移1个单位长度,再向上平移2个单位长度,则平移后抛物线的顶点坐标为 .
12.已知一条抛物线的形状、开口方向均与抛物线y=-2x2+9x相同,且它的顶点坐标为(-1,6),则这条抛物线的表达式为 .
13.关于x的二次函数y=ax2-4ax+b中,当1≤x≤4时,-3≤y≤5.则b-4a的值为 .
14.如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴相交于点A,B,点B的坐标为(3,0),若点C(2,3)在抛物线上,则AB的长为 .
15.九(1)班劳动实践基地内有一块面积足够大的平整空地,地上两段围墙AB⊥CD于点O(如图),其中AB上的EO段围墙空缺.同学们测得AE=6.6 m,OE=1.4 m,OB=6 m,OC=5 m,OD=3 m,班长买来可切断的围栏16 m,准备利用已有围墙,围出一块封闭的矩形菜地,则该菜地最大面积是
m2.
三、解答题(本题共8小题,共75分.解答应写出文字说明、演算步骤或推理过程)
16.(8分)已知二次函数y=x2-4x+3.
(1)求二次函数y=x2-4x+3图象的顶点坐标;
(2)在平面直角坐标系中,画出二次函数y=x2-4x+3的图象;
(3)当1
(1)求点B的坐标;
(2)当x 时,y随x的增大而减小;
(3)不等式ax2+bx+c>0的解集是什么
18.(8分)(2024济宁中考)某商场以每件80元的价格购进一种商品,在一段时间内,销售量y(单位:件)与销售单价x(单位:元/件)之间是一次函数关系,其部分图象如图所示.
(1)求这段时间内y与x之间的函数表达式;
(2)在这段时间内,若销售单价不低于100元,且商场还要完成不少于220件的销售任务,当销售单价为多少时,商场获得利润最大 最大利润是多少
19.(8分)已知二次函数y=2x2-mx-m2.
(1)求证:对于任意实数m,二次函数y=2x2-mx-m2的图象与x轴总有交点.
(2)若这个二次函数的图象与x轴交于点A,B(1,0),求点A的坐标.
20.(8分)如图,抛物线y=-x2+2x+c经过坐标原点O和点A,点A在x轴上.
(1)求此抛物线的表达式,并求出顶点B的坐标;
(2)连接OB,AB,求S△OAB;
(3)若点C在抛物线上,且S△OAC=8,求点C的坐标.
21.(10分)已知抛物线y=-x2+bx(b为常数)的顶点横坐标比抛物线y=-x2+2x的顶点横坐标大1.
(1)求b的值;
(2)点A(x1,y1)在抛物线y=-x2+2x上,点B(x1+t,y1+h)在抛物线y=-x2+bx上.
①若h=3t,且x1≥0,t>0,求h的值;
②若x1=t-1,求h的最大值.
22.(12分)(2024浙江中考)已知二次函数y=x2+bx+c(b,c为常数)的图象经过点A(-2,5),对称轴为直线x=-.
(1)求二次函数的表达式;
(2)若点B(1,7)向上平移2个单位长度,向左平移m(m>0)个单位长度后,恰好落在y=x2+bx+c的图象上,求m的值;
(3)当-2≤x≤n时,二次函数y=x2+bx+c的最大值与最小值的差为,求n的取值范围.
23.(13分)(2024辽宁中考)已知y1是自变量x的函数,当y2=xy1时,称函数y2为函数y1的“升幂函数”.在平面直角坐标系中,对于函数y1图象上任意一点A(m,n),称点B(m,mn)为点A“关于y1的升幂点”,点B在函数y1的“升幂函数”y2的图象上.
例如:函数y1=2x,当y2=xy1=x·2x=2x2时,则函数y2=2x2是函数y1=2x的“升幂函数”.在平面直角坐标系中,函数y1=2x的图象上任意一点A(m,2m),点B(m,2m2)为点A“关于y1的升幂点”,点B在函数y1=2x的“升幂函数”y2=2x2的图象上.
(1)求函数y1=x的“升幂函数”y2的函数表达式;
(2)如图,点A在函数y1=x>0的图象上,点A“关于y1的升幂点”B在点A上方,当AB=2时,求点A的坐标;
(3)点A在函数y1=-x+4的图象上,点A“关于y1的升幂点”为点B,设点A的横坐标为m.
①若点B与点A重合,求m的值;
②若点B在点A的上方,过点B作x轴的平行线,与函数y1的“升幂函数”y2的图象相交于点C,以AB,BC为邻边构造矩形ABCD,设矩形ABCD的周长为y,求y关于m的函数表达式;
③在②的条件下,当直线y=t1与函数y的图象的交点有3个时,从左到右依次记为E,F,G,当直线y=t2与函数y的图象的交点有2个时,从左到右依次记为M,N,若EF=MN,请直接写出t2-t1的值.
备用图
【详解答案】
1.B 解析:A.当a=0时,y=bx+c不是二次函数;B.y=x(x-1)=x2-x是二次函数;C.y=不是二次函数;D.y=(x-1)2-x2=
-2x+1为一次函数.故选B.
2.B 解析:由题意,根据函数的图象可得,二次函数y=-x2+mx+n的图象的对称轴是直线x=2,又图象与x轴的一个交点坐标为(5,0),∴图象与x轴的另一个交点坐标为(2-3,0),即(-1,0).∴关于x的一元二次方程-x2+mx+n=0的解为x1=5,x2=-1.故选B.
3.D 解析:∵y=(x-1)2+c,∴抛物线开口向上,对称轴是直线x=1,∴当x<1时,y随x的增大而减小,∵,y3关于直线x=1的对称点是-,y3,-2<-<0<1,∴y1>y3>y2.故选D.
4.D 解析:∵抛物线y=x2+1的对称轴为y轴,∴选项A不符合题意;∵抛物线y=x2-1的对称轴为y轴,∴选项B不符合题意;∵抛物线y=x2+2x=(x+1)2-1,∴该抛物线的对称轴为直线x=-1,∴选项C不符合题意;∵抛物线y=x2-2x=(x-1)2-1,∴该抛物线的对称轴为直线x=1,∴选项D符合题意.故选D.
5.B 解析:∵该厂今年一月份新产品的研发资金为10万元,以后每月新产品的研发资金与上月相比增长率都是x,∴该厂今年二月份新产品的研发资金为10(1+x)万元,三月份新产品的研发资金为10(1+x)2万元.根据题意得:y=10+10(1+x)+10(1+x)2.故选B.
6.C 解析:∵二次函数y=x2+a,∴抛物线开口向上,∴排除B,∵一次函数y=ax+2,∴直线与y轴的正半轴相交,
∴排除D;∵由抛物线得a<0,∴排除A;故选C.
7.D 解析:∵h=gt2,∴t==0.3(s),∵L
9.A 解析:由图象得:a>0,与x轴相交于点(-1,0)和(3,0),∴抛物线的对称轴为直线x==1,即-=1,∴b+2a=0,故①是正确的;由图象得:当x=1时,y<0,即a+b+c<0,故②是错误的;∵a>0,∴y=a在x轴的上方,∴y=ax2+bx+c的图象与y=a有两个交点,故③是正确的;y=ax2+bx+c的图象与x轴的交点为(-1,0),(3,0),∴不等式ax2+bx+c<0的解集是-1
-5(t-3)2+45,∵-5<0,∴当t=3时,h有最大值,最大值为45,∴小球运动中的高度可以是30 m,故②正确;③t=2时,h=30×2-5×4=40(m),t=5时,h=30×5-5×25=25(m),∴小球运动2 s时的高度大于运动5 s时的高度,故③错误.故选C.
11.(1,2) 解析:将抛物线y=-x2先向右平移1个单位长度,再向上平移2个单位长度后抛物线表达式为y=-(x-1)2+2,∴顶点坐标为(1,2).
12.y=-2(x+1)2+6 解析:∵抛物线的顶点坐标为(-1,6),∴抛物线表达式可设为y=a(x+1)2+6,∵抛物线y=a(x+1)2+6的形状、开口方向均与抛物线y=-2x2+9x相同,∴a=-2,∴所求抛物线的表达式为y=-2(x+1)2+6.
13.-3或5 解析:∵抛物线y=ax2-4ax+b=a(x-2)2+b-4a,∴顶点为(2,b-4a),当a>0时,当1≤x≤4时,-3≤y≤5,函数有最小值,∴b-4a=-3,当a<0时,当1≤x≤4时,-3≤y≤5,函数有最大值,∴b-4a=5,故b-4a的值为-3或5.
14.4 解析:∵抛物线y=ax2+bx+3过B(3,0),C(2,3),
∴∴抛物线为y=-x2+2x+3.∴抛物线的对称轴是直线x=-=1.∵抛物线与x轴的一交点为B(3,0),∴另一交点为A(1-2,0),即A(-1,0).∴AB=3-(-1)=4.
15.46.4 解析:设矩形在射线OA上的一段长为x m.
(1)当x≤8时,S=x·=-x2+9.8x=-(x-9.8)2+48.02,当x=8时,S=46.4,
(2)当x>8时,S=x·-x=-x2+13.8x=-(x-6.9)2+47.61,由于在x>8的范围内,S均小于46.4.所以由(1)(2)得最大面积为46.4 m2.
16.解:(1)∵y=x2-4x+3=(x-2)2-1,
∴该二次函数图象顶点坐标为(2,-1).
(2)当y=0时,x2-4x+3=0,解得x1=1,x2=3,
∴抛物线与x轴的交点坐标为(1,0),(3,0);
当x=0时,y=x2-4x+3=3,则抛物线与y轴的交点坐标为(0,3),关于对称轴的对称点为(4,3),
如图.
(3)由图象可知,当1
∵A(-1,0),
∴点B坐标为(3,0).
(2)>1
(3)由图象可知,不等式ax2+bx+c>0的解集是-1
又过(100,300),(120,200),
∴
∴
∴这段时间内y与x之间函数表达式为y=-5x+800.
(2)由题意得,
∴100≤x≤116.
∵商场获得的利润=(x-80)(-5x+800)
=-5x2+1 200x-64 000
=-5(x-120)2+8 000,
又-5<0,100≤x≤116,
∴当x=116时,利润最大,最大值为7 920.
答:当销售单价为116元/件时,商场获得利润最大,最大利润是7 920元.
19.解:(1)证明:∵Δ=(-m)2-4×2×(-m2)=9m2≥0,
∴对于任意实数m,二次函数y=2x2-mx-m2的图象与x轴总有交点.
(2)把B(1,0)代入y=2x2-mx-m2得2-m-m2=0,解得m1=-2,m2=1,
当m=-2时,抛物线表达式为y=2x2+2x-4,解方程2x2+2x-4=0,解得x1=-2,x2=1,此时点A坐标为(-2,0);
当m=1时,抛物线表达式为y=2x2-x-1,解方程2x2-x-1=0,解得x1=-,x2=1,此时A点坐标为-,0.
综上所述,A点坐标为(-2,0)或-,0.
20.解:(1)把(0,0)代入y=-x2+2x+c得c=0,
∴抛物线表达式为y=-x2+2x,
∴y=-x2+2x=-(x-1)2+1,
∴顶点B的坐标为(1,1).
(2)当y=0时,-x2+2x=0,
解得x1=0,x2=2,
∴A(2,0),
∴S△OAB=×2×1=1.
(3)设点C坐标为(t,-t2+2t),
∵S△OAC=8,
∴×2×|-t2+2t|=8,
即t2-2t=8或t2-2t=-8,
解方程t2-2t=8得t1=-2,t2=4,
∴点C坐标为(-2,-8)或(4,-8),
方程t2-2t=-8无实数解,
综上所述,点C坐标为(-2,-8)或(4,-8).
21.解:(1)∵抛物线y=-x2+bx的顶点横坐标为,y=-x2+2x的顶点横坐标为1,
∴-1=1,
∴b=4.
(2)∵点A(x1,y1)在抛物线y=-x2+2x上,
∴y1=-+2x1,
∵点B(x1+t,y1+h)在抛物线y=-x2+4x上,
∴y1+h=-(x1+t)2+4(x1+t),
-+2x1+h=-+4(x1+t),
∴h=-t2-2x1t+2x1+4t,
①∵h=3t,
∴3t=-t2-2x1t+2x1+4t,
∴t(t+2x1)=t+2x1,
∵x1≥0,t>0,
∴t+2x1>0,
∴t=1,
∴h=3.
②将x1=t-1代入h=-t2-2x1t+2x1+4t,
∴h=-3t2+8t-2,
h=-3,
∵-3<0,
∴当t=,即x1=时,h取最大值.
22.解:(1)∵二次函数为y=x2+bx+c,
∴抛物线的对称轴为直线x=-=-.
∴b=1.
∴抛物线为y=x2+x+c.
又∵图象经过点A(-2,5),
∴4-2+c=5.
∴c=3.
∴抛物线为y=x2+x+3.
(2)∵点B(1,7)向上平移2个单位长度,向左平移m个单位长度(m>0),
∴平移后的点为(1-m,9).
又∵(1-m,9)在y=x2+x+3上,
∴9=(1-m)2+(1-m)+3.
∴m=4或m=-1(舍去).
∴m=4.
(3)由题意,当n<-时,
∴最大值与最小值的差为5-=.
∴n1=n2=-,不符合题意,舍去.
当-≤n≤1时,
∴最大值与最小值的差为5-,符合题意.
当n>1时,最大值与最小值的差为-,解得n1=1或n2=-2,不符合题意.
综上所述,n的取值范围为-≤n≤1.
23.解:(1)y2=xy1=x×x=x2.
(2)如图1,
图1
∵y2=xy1=x×=3,
设Am,,B(m,3),
∵点B在点A的上方,
∴当AB=2时,3-=2,
解得m=3.
∴A(3,1).
(3)①∵y2=xy1=x(-x+4)=-x2+4x,
∴A(m,-m+4),B(m,-m2+4m).
如果点B与点A重合,那么-m+4=-m2+4m.
整理,得m2-5m+4=0.
解得m=1或m=4.
②由①可知,直线y=-x+4与抛物线y=-x2+4x有两个交点(1,3)和(4,0),
如图2所示,函数y2=-x2+4x的图象是开口向下的抛物线,对称轴是直线x=2.
图2
∵BC∥x轴,∴B,C两点关于直线x=2对称.
如图2,当点B在点C右侧时,2
当2
图3
③t2-t1=4或3-2.
解析:情形1:如图4,如果EF和MN平行且相等,那这两条平行线间的距离等于两个顶点之间的竖直高度,或者等于P,Q两点间的竖直高度.
当m=2时,y=-2m2+6m=4,
∴P(2,4).
当m=4时,y=-2m2+14m-16=8,
∴Q(4,8).
∴t2-t1=8-4=4.
图4
情形2,如图5(图4局部,变形处理),点M是抛物线y=-2m2+6m的顶点.
由M,,得N,,
∴MN=EF=-=2-,
∴点F的横坐标xF=,
于是可得yF=,
∴t2-t1=yN-yF=-=3-2.
图5
综上,t2-t1=4或3-2.
