第三章 圆 评估测试卷 (含答案) 2024-2025学年数学北师大版九年级下册
文档属性
| 名称 | 第三章 圆 评估测试卷 (含答案) 2024-2025学年数学北师大版九年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 378.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-26 00:00:00 | ||
图片预览



文档简介
第三章 圆 评估测试卷
(满分:120分 时间:120分钟)
一、选择题(本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
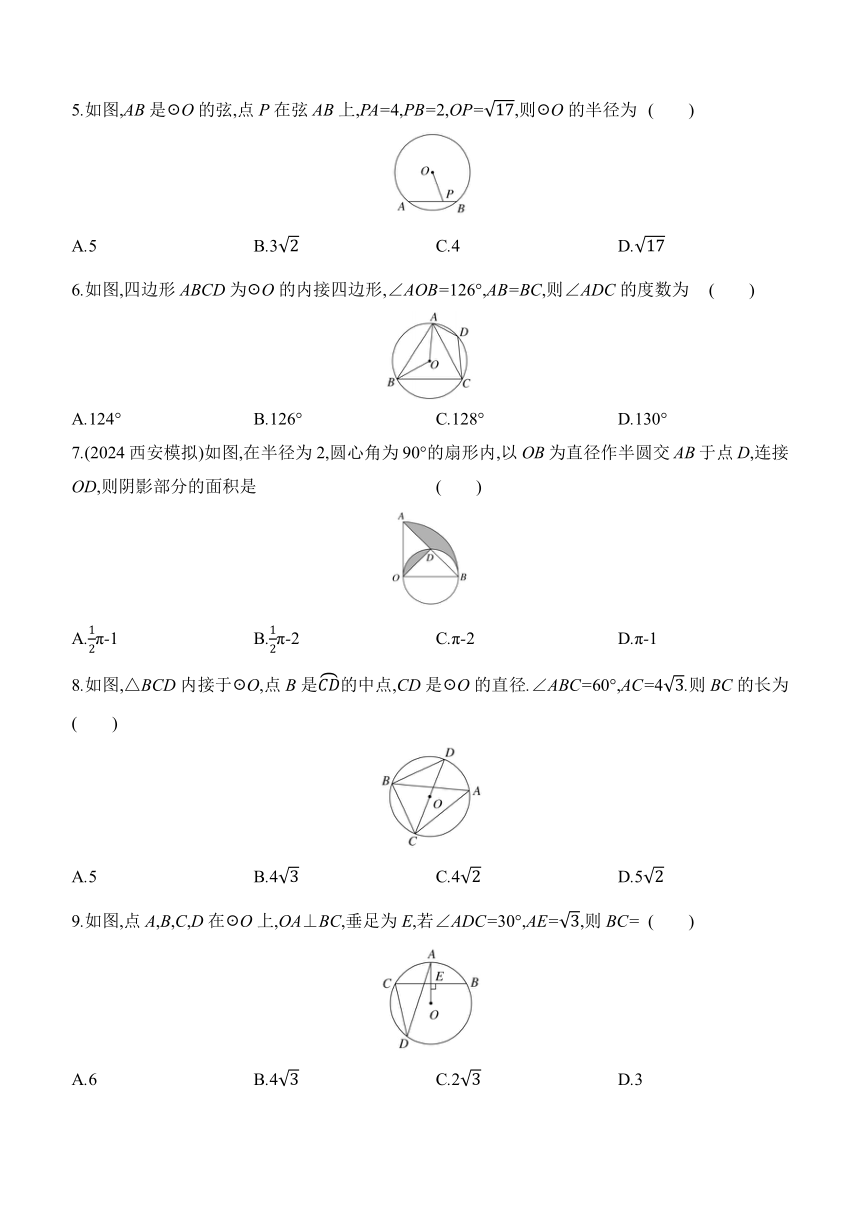
1.下列说法:①直径是弦;②经过三个点一定可以作圆;③三角形的外心到三角形各顶点的距离都相等;④相等的圆心角所对的弧相等.其中正确的有 ( )
A.4个 B.3个 C.2个 D.1个
2.如图,☉O是△ABC的外接圆,AC是☉O的直径,点P在☉O上,若∠ACB=35°,则∠BPC的度数是( )
A.35° B.45°
C.55° D.65°
3.如图,若△ABC的三边长分别为AB=9,BC=5,CA=6,△ABC的内切圆☉O与AB,BC,CA分别切于点D,E,F,则AF的长为 ( )
A.5 B.10
C.7.5 D.4
4.如图,正五边形ABCDE内接于☉O,P为上的一点(点P不与点D重合),则∠CPD的度数为( )
A.30° B.36°
C.40° D.43°
5.如图,AB是☉O的弦,点P在弦AB上,PA=4,PB=2,OP=,则☉O的半径为 ( )
A.5 B.3 C.4 D.
6.如图,四边形ABCD为☉O的内接四边形,∠AOB=126°,AB=BC,则∠ADC的度数为 ( )
A.124° B.126° C.128° D.130°
7.(2024西安模拟)如图,在半径为2,圆心角为90°的扇形内,以OB为直径作半圆交AB于点D,连接OD,则阴影部分的面积是 ( )
A.π-1 B.π-2 C.π-2 D.π-1
8.如图,△BCD内接于☉O,点B是的中点,CD是☉O的直径.∠ABC=60°,AC=4.则BC的长为( )
A.5 B.4 C.4 D.5
9.如图,点A,B,C,D在☉O上,OA⊥BC,垂足为E,若∠ADC=30°,AE=,则BC= ( )
A.6 B.4 C.2 D.3
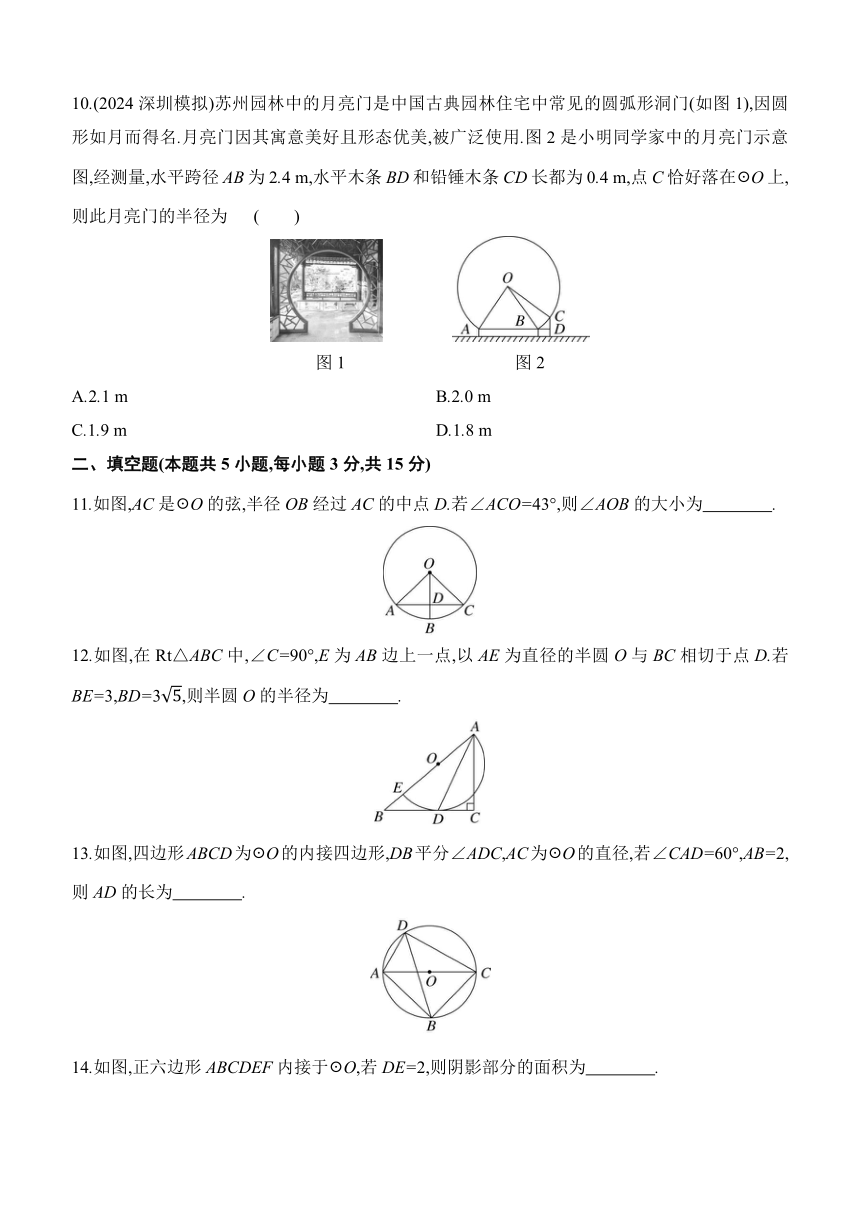
10.(2024深圳模拟)苏州园林中的月亮门是中国古典园林住宅中常见的圆弧形洞门(如图1),因圆形如月而得名.月亮门因其寓意美好且形态优美,被广泛使用.图2是小明同学家中的月亮门示意图,经测量,水平跨径AB为2.4 m,水平木条BD和铅锤木条CD长都为0.4 m,点C恰好落在☉O上,则此月亮门的半径为 ( )
图1 图2
A.2.1 m B.2.0 m
C.1.9 m D.1.8 m
二、填空题(本题共5小题,每小题3分,共15分)
11.如图,AC是☉O的弦,半径OB经过AC的中点D.若∠ACO=43°,则∠AOB的大小为 .
12.如图,在Rt△ABC中,∠C=90°,E为AB边上一点,以AE为直径的半圆O与BC相切于点D.若BE=3,BD=3,则半圆O的半径为 .
13.如图,四边形ABCD为☉O的内接四边形,DB平分∠ADC,AC为☉O的直径,若∠CAD=60°,AB=2,则AD的长为 .
14.如图,正六边形ABCDEF内接于☉O,若DE=2,则阴影部分的面积为 .
15.如图,四边形ABCD是边长为1的正方形,曲线DA1B1C1D1A2…是由多段90°的圆心角所对的弧组成的,其中,弧DA1的圆心为A,半径为AD;弧A1B1的圆心为B,半径为BA1;弧B1C1的圆心为C,半径为CB1;弧C1D1的圆心为D,半径为DC1……弧DA1、弧A1B1、弧B1C1、弧C1D1、…的圆心依次按点A、B、C、D循环,则弧C2 023D2 023的长是 (结果保留π).
三、解答题(本题共8小题,共75分.解答应写出文字说明、演算步骤或推理过程)
16.(5分)如图,A是半圆上靠近点N的一个三等分点,B是的中点,P是直径MN上一动点,☉O的半径为1,则PA+PB的最小值是多少
17.(8分)(2024通辽中考)如图,在△ABC中,∠ACB=90°,点O为AC边上一点,以点O为圆心,OC为半径作圆与AB相切于点D,连接CD.
(1)求证:∠ABC=2∠ACD;
(2)若AC=8,BC=6,求☉O的半径.
18.(8分)如图,在☉O中,AB、AC为弦,CD为直径,AB⊥CD于E,BF⊥AC于F,BF与CD相交于G.
(1)求证:ED=EG;
(2)若AB=4,OG=2,求☉O的半径.
19.(8分)已知:如图,AB是☉O的直径,弦CD⊥AB,垂足为E,∠AOC=60°,AC=2.
(1)求弦CD的长;
(2)求图中阴影部分的面积.
20.(10分)(2024安徽中考)如图,☉O是△ABC的外接圆,D是直径AB上一点,∠ACD的平分线交AB于点E,交☉O于另一点F,FA=FE.
(1)求证:CD⊥AB;
(2)设FM⊥AB,垂足为M,若OM=OE=1,求AC的长.
21.(12分)(2024威海中考)如图,已知AB是☉O的直径,点C,D在☉O上,且BC=CD.点E是线段AB延长线上一点,连接EC并延长交射线AD于点F.∠FEG的平分线EH交射线AC于点H,∠H=45°.
(1)求证:EF是☉O的切线;
(2)若BE=2,CE=4,求AF的长.
22.(12分)(2024浙江中考)如图,在圆内接四边形ABCD中,AD(1)若∠AFE=60°,CD为圆的直径,求∠ABD的度数.
(2)求证:①EF∥BC;
②EF=BD.
23.(12分)如图,正六边形ABCDEF为☉O的内接正六边形,过点D作☉O的切线,交AF的延长线于点P,连接FD,AD,☉O的半径为6.
(1)求∠ADF的度数;
(2)求线段PD的长;
(3)若点M为FD上一点(不与点F,D重合),连接AM,CM,直接写出△AFM与△CDM的面积之和.
【详解答案】
1.C 解析:直径是圆内最长的弦,故①正确;
任意不在同一直线上的三个点确定一个圆,故②错误;
三角形的外心到三角形各顶点的距离都相等,故③正确;
在同圆或等圆中,相等的圆心角所对的弧相等,故④错误.故选C.
2.C 解析:∵AC是☉O的直径,∴∠ABC=90°,∴∠A=90°-∠ACB=90°-35°=55°,∵∠A和∠BPC都是所对的圆周角,∴∠BPC=∠A=55°.故选C.
3.A 解析:设AF=x,根据切线长定理得AD=x,
BD=BE=9-x,
CE=CF=CA-AF=6-x,
则有9-x+6-x=5,解得x=5,即AF的长为5.故选A.
4.B 解析:连接OC,OD,如图,
∵五边形ABCDE是正五边形,∴∠COD==72°,∴∠CPD=∠COD=36°.故选B.
5.A 解析:如图,过O作OH⊥AB于H,连接OA,∴AH=AB,∵PA=4,PB=2,∴AB=4+2=6,∴AH=3,
∴PH=AP-AH=4-3=1,∵OP=,∴OH==4,∴OA==5.∴☉O的半径长是5.故选A.
6.B 解析:∵∠AOB=126°,∴∠ACB=∠AOB=63°,∵AB=BC,∴∠BAC=∠ACB=63°,
∴∠ABC=180°-∠BAC-∠ACB=180°-63°-63°=54°,∴∠ADC=180°-∠ABC=180°-54°=126°.故选B.
7.C 解析:由题意可知OA=OB=2,∠AOB=90°,∴∠ABO=∠BAO=45°,∵OB为直径,∴∠ODB=90°,∴∠DOB=
∠DBO=45°,∴OD=BD,∴弓形OD的面积=弓形BD的面积,∴阴影部分的面积=扇形AOB的面积-△AOB的面积=-×2×2=π-2.故选C.
8.C 解析:如图,连接AD,∵CD是☉O的直径,∴∠CAD=∠CBD=90°,∵∠ABC=60°,AC=4,
∴∠ACD=∠ABD=30°,∴AD=AC=4,∴CD=2AD=8,∵点B是的中点,∴BC=BD,
∵∠CBD=90°,∴BC2+BD2=CD2,即2BC2=64,解得BC=4.故选C.
9.A 解析:如图,连接OC,∵∠ADC=30°,∴∠AOC=2∠ADC=60°,∵OA⊥BC,∴BE=EC,∠OEC=90°,
∴∠OCE=30°,∴OC=2OE,∵AE=,∴OC=2,∴OE=,
∴EC==3,∴BC=6.故选A.
10.B 解析:过O作ON⊥AB于N,过C作CM⊥ON于M,如图所示,则AN=NB=AB=1.2 m,∠OND=∠CMN=90°,∵DC⊥AB,∴∠CDN=90°,∴四边形CDNM是矩形,∴MN=CD=0.4 m,CM=DN=BD+BN=1.6(m),设该圆的半径长为r m,根据题意得,ON-OM=0.4 m,∴-=0.4,∴r=2.0,经检验,r=2.0是方程的根,即此月亮门的半径为2.0 m.故选B.
11.47° 解析:∵半径OB经过AC的中点D,∴OB⊥AC,∵OC=OA,∴∠AOB=∠BOC,∵∠ACO=43°,OB⊥AC,
∴∠AOB=∠BOC=90°-43°=47°.
12.6 解析:连接OD,如图所示.
∵BC与半圆O相切于点D,∴OD⊥BC.设半圆O的半径为r,则OB=3+r,OD=r.在Rt△BOD中,+r2=(3+r)2,解得r=6,∴半圆O的半径为6.
13. 解析:∵AC为☉O的直径,∴∠ADC=∠ABC=90°,∵DB平分∠ADC,∴∠ADB=∠CDB=∠ADC=45°,
∴,∴AB=BC,
∴△ABC是等腰直角三角形,∴AC=AB=2,∵∠CAD=60°,∴∠ACD=30°,∴AD=AC=.
14. 解析:连接OA、OB、OF、OC、OD,BF交DA于点M,作ON⊥CD于点N,如图,
∵正六边形ABCDEF内接于☉O,∴四边形AFOB是菱形,∵DE=2,∴OA=2,BM=,ON=,∴BF=2,
∴S△AFB=×2×2,S扇形OCD=,S△OCD=×2×,∴S阴影=-.
15.4 046π 解析:弧DA1的半径是1,弧A1B1的半径是2,弧B1C1的半径是3,弧C1D1的半径是4;弧D1A2的半径是5,弧A2B2的半径是6……弧C2D2的半径是8=4×2……弧C3D3的半径是12=4×3……∴弧CnDn的半径是4n.即弧C2 023D2 023的半径为DD2 023=4n=4×2 023=8 092,
∴弧C2 023D2 023的长是==4 046π.
16.解:如图,过点B作BB'⊥MN交☉O于点B',连接AB'交MN于点P,连接OB',OB,PB,
此时PA+PB=PA+PB'=AB'最小.
∵A是半圆的一个三等分点.
∴∠AON=60°.
又∵,
∴∠BON=∠B'ON=30°,
∴∠AOB'=90°.
∵AO=OB'=1,∴AB'=.
∴PA+PB的最小值是.
17.解:(1)证明:连接OD,如图,
∵AB为☉O的切线,
∴OD⊥AB,
∴∠ODA=∠ODB=90°,
∵∠ACB=90°,
∴∠ABC+∠COD=180°,
∵∠AOD+∠COD=180°,
∴∠ABC=∠AOD,
∵∠AOD=2∠ACD,
∴∠ABC=2∠ACD.
(2)设☉O的半径为r,则OD=OC=r,OA=8-r,
在Rt△ACB中,
∵∠ACB=90°,AC=8,BC=6,
∴AB==10,
∵∠OAD=∠BAC,∠ADO=∠ACB,
∴△AOD∽△ABC,
∴,即,
解得r=3,
即☉O的半径为3.
18.解:(1)证明:如图,连接BD,
∵AB⊥CD于E,BF⊥AC于F,
∴∠CFG=∠GEB=90°
又∵∠CGF=∠BGE,
∴∠C=∠GBE,
∵,
∴∠C=∠DBE,
∴∠GBE=∠DBE,
∵AB⊥CD,
∴∠GEB=∠DEB=90°,
∴∠BGE=∠BDE,
∴BD=BG,
又∵BE⊥DG,
∴ED=EG.
(2)如图,连接OA,设OA=r,则DG=r+2,
∴ED=EG=,
∴OE=,
∵AB⊥CD于E,AB=4,
∴AE=AB=2,
在Rt△OEA中,OE2+AE2=OA2,
即+20=r2,
解得r=或r=-6(舍).
即☉O的半径为.
19.解:(1)∵AB是☉O的直径,
∴∠ACB=90°,
∵AC=2,∠AOC=60°,
∴△AOC是等边三角形,
则OC=AC=2,AB=4,
∵弦CD⊥AB,
∴CE=DE=CD=OC×sin 60°=2×,
∴CD=2CE=2.
(2)∵S△ABC=AB·CE=×4×=2,
∴S阴影=S半圆-S△ABC=π·22-2=2π-2.
20.解:(1)证明:∵FA=FE,
∴∠FAE=∠AEF,
∵∠FAE与∠BCE都是所对的圆周角,
∴∠FAE=∠BCE,
∵∠AEF=∠CEB,
∴∠CEB=∠BCE,
∵CE平分∠ACD,
∴∠ACE=∠DCE,
∵AB是直径,
∴∠ACB=90°,
∴∠CEB+∠DCE=∠BCE+∠ACE=∠ACB=90°,
∴∠CDE=90°,
∴CD⊥AB.
(2)由(1)知,∠BEC=∠BCE,
∴BE=BC,
∵AF=EF,FM⊥AB,
∴MA=ME=2,AE=4,
∴圆的半径OA=OB=AE-OE=3,
∴BC=BE=OB-OE=2,
在△ABC中,AB=6,BC=2,
∠ACB=90°,
∴AC==4.
21.解:(1)证明:如图,连接OC,
∵OA=OC,
∴∠OAC=∠OCA,
∵BC=CD,
∴∠DAC=∠BAC,
∴∠OCA=∠DAC,
∴OC∥AF.
∵EH平分∠FEG,
∴∠FEH=∠GEH,
∵∠GEH=∠H+∠BAC,∠FEG=∠F+∠BAF,
∴2∠H+2∠BAC=∠F+∠BAF,
∵∠BAF=2∠BAC,
∴∠F=2∠H=90°,
∴∠OCE=∠F=90°,
即OC⊥EF,
∵OC是半径,
∴EF是☉O的切线.
(2)∵AB是☉O的直径,
∴∠ACB=90°,
∴∠OBC+∠BAC=90°,
∵EF是☉O的切线,
∴∠OCB+∠BCE=90°.
又∵OB=OC,
∴∠OBC=∠OCB,
∴∠BCE=∠EAC,
∵∠CEB=∠AEC,
∴△BCE∽△CAE,
∴,
∴CE2=BE·AE,即16=2AE,
解得AE=8,
∴AB=8-2=6,
在Rt△ABC中,AB=6,,
∴BC=,AC=,
∵∠F=∠ACB=90°,∠FAC=∠BAC,
∴△FAC∽△CAB,
∴,∴AF=.
22.解:(1)∵CD为直径,
∴∠CAD=90°,
∵∠AFE=∠ADC=60°,
∴∠ACD=90°-60°=30°.
∴∠ABD=∠ACD=30°.
(2)证明:①如图,延长AB,
∵四边形ABCD是圆内接四边形,
∴∠CBM=∠ADC,
又∵∠AFE=∠ADC,
∴∠AFE=∠CBM,
∴EF∥BC.
②过点D作DG∥BC交圆于点G,连接AG,CG,
∵DG∥BC,
∴,∴BD=CG,
∵四边形ACGD是圆内接四边形,
∴∠GDE=∠ACG,
∵EF∥DG,
∴∠DEF=∠GDE,
∴∠DEF=∠ACG,
∵∠AFE=∠ADC,∠ADC=∠AGC,
∴∠AFE=∠AGC,
∵AE=AC,∴△AEF≌△ACG(AAS),
∴EF=CG,∴EF=BD.
23.解:(1)如图,连接FO,
∵正六边形ABCDEF为☉O的内接正六边形,
∴AD为☉O的直径,∠AFD=90°,
∴∠AOF=60°,
∴∠ADF=∠AOF=30°.
(2)∵PD与☉O相切,AD为☉O的直径,
∴∠ADP=90°.
∵正六边形ABCDEF为☉O的内接正六边形,
∴∠PAD=60°,
在Rt△PAD中,AD=12,
∴PD=AD·tan 60°=12×=12.
(3)S△AFM+S△CDM=18.
解析:S△AFM+S△CDM=S△AFM+S△AMD=
S△AFD,
在Rt△AFD中,
AF=AD·cos∠FAD=12×cos 60°=6,
DF=AD·sin∠FAD=12×sin 60°=6,
∴S△AFD=×6×6=18,
∴S△AFM+S△CDM=18.
(满分:120分 时间:120分钟)
一、选择题(本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列说法:①直径是弦;②经过三个点一定可以作圆;③三角形的外心到三角形各顶点的距离都相等;④相等的圆心角所对的弧相等.其中正确的有 ( )
A.4个 B.3个 C.2个 D.1个
2.如图,☉O是△ABC的外接圆,AC是☉O的直径,点P在☉O上,若∠ACB=35°,则∠BPC的度数是( )
A.35° B.45°
C.55° D.65°
3.如图,若△ABC的三边长分别为AB=9,BC=5,CA=6,△ABC的内切圆☉O与AB,BC,CA分别切于点D,E,F,则AF的长为 ( )
A.5 B.10
C.7.5 D.4
4.如图,正五边形ABCDE内接于☉O,P为上的一点(点P不与点D重合),则∠CPD的度数为( )
A.30° B.36°
C.40° D.43°
5.如图,AB是☉O的弦,点P在弦AB上,PA=4,PB=2,OP=,则☉O的半径为 ( )
A.5 B.3 C.4 D.
6.如图,四边形ABCD为☉O的内接四边形,∠AOB=126°,AB=BC,则∠ADC的度数为 ( )
A.124° B.126° C.128° D.130°
7.(2024西安模拟)如图,在半径为2,圆心角为90°的扇形内,以OB为直径作半圆交AB于点D,连接OD,则阴影部分的面积是 ( )
A.π-1 B.π-2 C.π-2 D.π-1
8.如图,△BCD内接于☉O,点B是的中点,CD是☉O的直径.∠ABC=60°,AC=4.则BC的长为( )
A.5 B.4 C.4 D.5
9.如图,点A,B,C,D在☉O上,OA⊥BC,垂足为E,若∠ADC=30°,AE=,则BC= ( )
A.6 B.4 C.2 D.3
10.(2024深圳模拟)苏州园林中的月亮门是中国古典园林住宅中常见的圆弧形洞门(如图1),因圆形如月而得名.月亮门因其寓意美好且形态优美,被广泛使用.图2是小明同学家中的月亮门示意图,经测量,水平跨径AB为2.4 m,水平木条BD和铅锤木条CD长都为0.4 m,点C恰好落在☉O上,则此月亮门的半径为 ( )
图1 图2
A.2.1 m B.2.0 m
C.1.9 m D.1.8 m
二、填空题(本题共5小题,每小题3分,共15分)
11.如图,AC是☉O的弦,半径OB经过AC的中点D.若∠ACO=43°,则∠AOB的大小为 .
12.如图,在Rt△ABC中,∠C=90°,E为AB边上一点,以AE为直径的半圆O与BC相切于点D.若BE=3,BD=3,则半圆O的半径为 .
13.如图,四边形ABCD为☉O的内接四边形,DB平分∠ADC,AC为☉O的直径,若∠CAD=60°,AB=2,则AD的长为 .
14.如图,正六边形ABCDEF内接于☉O,若DE=2,则阴影部分的面积为 .
15.如图,四边形ABCD是边长为1的正方形,曲线DA1B1C1D1A2…是由多段90°的圆心角所对的弧组成的,其中,弧DA1的圆心为A,半径为AD;弧A1B1的圆心为B,半径为BA1;弧B1C1的圆心为C,半径为CB1;弧C1D1的圆心为D,半径为DC1……弧DA1、弧A1B1、弧B1C1、弧C1D1、…的圆心依次按点A、B、C、D循环,则弧C2 023D2 023的长是 (结果保留π).
三、解答题(本题共8小题,共75分.解答应写出文字说明、演算步骤或推理过程)
16.(5分)如图,A是半圆上靠近点N的一个三等分点,B是的中点,P是直径MN上一动点,☉O的半径为1,则PA+PB的最小值是多少
17.(8分)(2024通辽中考)如图,在△ABC中,∠ACB=90°,点O为AC边上一点,以点O为圆心,OC为半径作圆与AB相切于点D,连接CD.
(1)求证:∠ABC=2∠ACD;
(2)若AC=8,BC=6,求☉O的半径.
18.(8分)如图,在☉O中,AB、AC为弦,CD为直径,AB⊥CD于E,BF⊥AC于F,BF与CD相交于G.
(1)求证:ED=EG;
(2)若AB=4,OG=2,求☉O的半径.
19.(8分)已知:如图,AB是☉O的直径,弦CD⊥AB,垂足为E,∠AOC=60°,AC=2.
(1)求弦CD的长;
(2)求图中阴影部分的面积.
20.(10分)(2024安徽中考)如图,☉O是△ABC的外接圆,D是直径AB上一点,∠ACD的平分线交AB于点E,交☉O于另一点F,FA=FE.
(1)求证:CD⊥AB;
(2)设FM⊥AB,垂足为M,若OM=OE=1,求AC的长.
21.(12分)(2024威海中考)如图,已知AB是☉O的直径,点C,D在☉O上,且BC=CD.点E是线段AB延长线上一点,连接EC并延长交射线AD于点F.∠FEG的平分线EH交射线AC于点H,∠H=45°.
(1)求证:EF是☉O的切线;
(2)若BE=2,CE=4,求AF的长.
22.(12分)(2024浙江中考)如图,在圆内接四边形ABCD中,AD
(2)求证:①EF∥BC;
②EF=BD.
23.(12分)如图,正六边形ABCDEF为☉O的内接正六边形,过点D作☉O的切线,交AF的延长线于点P,连接FD,AD,☉O的半径为6.
(1)求∠ADF的度数;
(2)求线段PD的长;
(3)若点M为FD上一点(不与点F,D重合),连接AM,CM,直接写出△AFM与△CDM的面积之和.
【详解答案】
1.C 解析:直径是圆内最长的弦,故①正确;
任意不在同一直线上的三个点确定一个圆,故②错误;
三角形的外心到三角形各顶点的距离都相等,故③正确;
在同圆或等圆中,相等的圆心角所对的弧相等,故④错误.故选C.
2.C 解析:∵AC是☉O的直径,∴∠ABC=90°,∴∠A=90°-∠ACB=90°-35°=55°,∵∠A和∠BPC都是所对的圆周角,∴∠BPC=∠A=55°.故选C.
3.A 解析:设AF=x,根据切线长定理得AD=x,
BD=BE=9-x,
CE=CF=CA-AF=6-x,
则有9-x+6-x=5,解得x=5,即AF的长为5.故选A.
4.B 解析:连接OC,OD,如图,
∵五边形ABCDE是正五边形,∴∠COD==72°,∴∠CPD=∠COD=36°.故选B.
5.A 解析:如图,过O作OH⊥AB于H,连接OA,∴AH=AB,∵PA=4,PB=2,∴AB=4+2=6,∴AH=3,
∴PH=AP-AH=4-3=1,∵OP=,∴OH==4,∴OA==5.∴☉O的半径长是5.故选A.
6.B 解析:∵∠AOB=126°,∴∠ACB=∠AOB=63°,∵AB=BC,∴∠BAC=∠ACB=63°,
∴∠ABC=180°-∠BAC-∠ACB=180°-63°-63°=54°,∴∠ADC=180°-∠ABC=180°-54°=126°.故选B.
7.C 解析:由题意可知OA=OB=2,∠AOB=90°,∴∠ABO=∠BAO=45°,∵OB为直径,∴∠ODB=90°,∴∠DOB=
∠DBO=45°,∴OD=BD,∴弓形OD的面积=弓形BD的面积,∴阴影部分的面积=扇形AOB的面积-△AOB的面积=-×2×2=π-2.故选C.
8.C 解析:如图,连接AD,∵CD是☉O的直径,∴∠CAD=∠CBD=90°,∵∠ABC=60°,AC=4,
∴∠ACD=∠ABD=30°,∴AD=AC=4,∴CD=2AD=8,∵点B是的中点,∴BC=BD,
∵∠CBD=90°,∴BC2+BD2=CD2,即2BC2=64,解得BC=4.故选C.
9.A 解析:如图,连接OC,∵∠ADC=30°,∴∠AOC=2∠ADC=60°,∵OA⊥BC,∴BE=EC,∠OEC=90°,
∴∠OCE=30°,∴OC=2OE,∵AE=,∴OC=2,∴OE=,
∴EC==3,∴BC=6.故选A.
10.B 解析:过O作ON⊥AB于N,过C作CM⊥ON于M,如图所示,则AN=NB=AB=1.2 m,∠OND=∠CMN=90°,∵DC⊥AB,∴∠CDN=90°,∴四边形CDNM是矩形,∴MN=CD=0.4 m,CM=DN=BD+BN=1.6(m),设该圆的半径长为r m,根据题意得,ON-OM=0.4 m,∴-=0.4,∴r=2.0,经检验,r=2.0是方程的根,即此月亮门的半径为2.0 m.故选B.
11.47° 解析:∵半径OB经过AC的中点D,∴OB⊥AC,∵OC=OA,∴∠AOB=∠BOC,∵∠ACO=43°,OB⊥AC,
∴∠AOB=∠BOC=90°-43°=47°.
12.6 解析:连接OD,如图所示.
∵BC与半圆O相切于点D,∴OD⊥BC.设半圆O的半径为r,则OB=3+r,OD=r.在Rt△BOD中,+r2=(3+r)2,解得r=6,∴半圆O的半径为6.
13. 解析:∵AC为☉O的直径,∴∠ADC=∠ABC=90°,∵DB平分∠ADC,∴∠ADB=∠CDB=∠ADC=45°,
∴,∴AB=BC,
∴△ABC是等腰直角三角形,∴AC=AB=2,∵∠CAD=60°,∴∠ACD=30°,∴AD=AC=.
14. 解析:连接OA、OB、OF、OC、OD,BF交DA于点M,作ON⊥CD于点N,如图,
∵正六边形ABCDEF内接于☉O,∴四边形AFOB是菱形,∵DE=2,∴OA=2,BM=,ON=,∴BF=2,
∴S△AFB=×2×2,S扇形OCD=,S△OCD=×2×,∴S阴影=-.
15.4 046π 解析:弧DA1的半径是1,弧A1B1的半径是2,弧B1C1的半径是3,弧C1D1的半径是4;弧D1A2的半径是5,弧A2B2的半径是6……弧C2D2的半径是8=4×2……弧C3D3的半径是12=4×3……∴弧CnDn的半径是4n.即弧C2 023D2 023的半径为DD2 023=4n=4×2 023=8 092,
∴弧C2 023D2 023的长是==4 046π.
16.解:如图,过点B作BB'⊥MN交☉O于点B',连接AB'交MN于点P,连接OB',OB,PB,
此时PA+PB=PA+PB'=AB'最小.
∵A是半圆的一个三等分点.
∴∠AON=60°.
又∵,
∴∠BON=∠B'ON=30°,
∴∠AOB'=90°.
∵AO=OB'=1,∴AB'=.
∴PA+PB的最小值是.
17.解:(1)证明:连接OD,如图,
∵AB为☉O的切线,
∴OD⊥AB,
∴∠ODA=∠ODB=90°,
∵∠ACB=90°,
∴∠ABC+∠COD=180°,
∵∠AOD+∠COD=180°,
∴∠ABC=∠AOD,
∵∠AOD=2∠ACD,
∴∠ABC=2∠ACD.
(2)设☉O的半径为r,则OD=OC=r,OA=8-r,
在Rt△ACB中,
∵∠ACB=90°,AC=8,BC=6,
∴AB==10,
∵∠OAD=∠BAC,∠ADO=∠ACB,
∴△AOD∽△ABC,
∴,即,
解得r=3,
即☉O的半径为3.
18.解:(1)证明:如图,连接BD,
∵AB⊥CD于E,BF⊥AC于F,
∴∠CFG=∠GEB=90°
又∵∠CGF=∠BGE,
∴∠C=∠GBE,
∵,
∴∠C=∠DBE,
∴∠GBE=∠DBE,
∵AB⊥CD,
∴∠GEB=∠DEB=90°,
∴∠BGE=∠BDE,
∴BD=BG,
又∵BE⊥DG,
∴ED=EG.
(2)如图,连接OA,设OA=r,则DG=r+2,
∴ED=EG=,
∴OE=,
∵AB⊥CD于E,AB=4,
∴AE=AB=2,
在Rt△OEA中,OE2+AE2=OA2,
即+20=r2,
解得r=或r=-6(舍).
即☉O的半径为.
19.解:(1)∵AB是☉O的直径,
∴∠ACB=90°,
∵AC=2,∠AOC=60°,
∴△AOC是等边三角形,
则OC=AC=2,AB=4,
∵弦CD⊥AB,
∴CE=DE=CD=OC×sin 60°=2×,
∴CD=2CE=2.
(2)∵S△ABC=AB·CE=×4×=2,
∴S阴影=S半圆-S△ABC=π·22-2=2π-2.
20.解:(1)证明:∵FA=FE,
∴∠FAE=∠AEF,
∵∠FAE与∠BCE都是所对的圆周角,
∴∠FAE=∠BCE,
∵∠AEF=∠CEB,
∴∠CEB=∠BCE,
∵CE平分∠ACD,
∴∠ACE=∠DCE,
∵AB是直径,
∴∠ACB=90°,
∴∠CEB+∠DCE=∠BCE+∠ACE=∠ACB=90°,
∴∠CDE=90°,
∴CD⊥AB.
(2)由(1)知,∠BEC=∠BCE,
∴BE=BC,
∵AF=EF,FM⊥AB,
∴MA=ME=2,AE=4,
∴圆的半径OA=OB=AE-OE=3,
∴BC=BE=OB-OE=2,
在△ABC中,AB=6,BC=2,
∠ACB=90°,
∴AC==4.
21.解:(1)证明:如图,连接OC,
∵OA=OC,
∴∠OAC=∠OCA,
∵BC=CD,
∴∠DAC=∠BAC,
∴∠OCA=∠DAC,
∴OC∥AF.
∵EH平分∠FEG,
∴∠FEH=∠GEH,
∵∠GEH=∠H+∠BAC,∠FEG=∠F+∠BAF,
∴2∠H+2∠BAC=∠F+∠BAF,
∵∠BAF=2∠BAC,
∴∠F=2∠H=90°,
∴∠OCE=∠F=90°,
即OC⊥EF,
∵OC是半径,
∴EF是☉O的切线.
(2)∵AB是☉O的直径,
∴∠ACB=90°,
∴∠OBC+∠BAC=90°,
∵EF是☉O的切线,
∴∠OCB+∠BCE=90°.
又∵OB=OC,
∴∠OBC=∠OCB,
∴∠BCE=∠EAC,
∵∠CEB=∠AEC,
∴△BCE∽△CAE,
∴,
∴CE2=BE·AE,即16=2AE,
解得AE=8,
∴AB=8-2=6,
在Rt△ABC中,AB=6,,
∴BC=,AC=,
∵∠F=∠ACB=90°,∠FAC=∠BAC,
∴△FAC∽△CAB,
∴,∴AF=.
22.解:(1)∵CD为直径,
∴∠CAD=90°,
∵∠AFE=∠ADC=60°,
∴∠ACD=90°-60°=30°.
∴∠ABD=∠ACD=30°.
(2)证明:①如图,延长AB,
∵四边形ABCD是圆内接四边形,
∴∠CBM=∠ADC,
又∵∠AFE=∠ADC,
∴∠AFE=∠CBM,
∴EF∥BC.
②过点D作DG∥BC交圆于点G,连接AG,CG,
∵DG∥BC,
∴,∴BD=CG,
∵四边形ACGD是圆内接四边形,
∴∠GDE=∠ACG,
∵EF∥DG,
∴∠DEF=∠GDE,
∴∠DEF=∠ACG,
∵∠AFE=∠ADC,∠ADC=∠AGC,
∴∠AFE=∠AGC,
∵AE=AC,∴△AEF≌△ACG(AAS),
∴EF=CG,∴EF=BD.
23.解:(1)如图,连接FO,
∵正六边形ABCDEF为☉O的内接正六边形,
∴AD为☉O的直径,∠AFD=90°,
∴∠AOF=60°,
∴∠ADF=∠AOF=30°.
(2)∵PD与☉O相切,AD为☉O的直径,
∴∠ADP=90°.
∵正六边形ABCDEF为☉O的内接正六边形,
∴∠PAD=60°,
在Rt△PAD中,AD=12,
∴PD=AD·tan 60°=12×=12.
(3)S△AFM+S△CDM=18.
解析:S△AFM+S△CDM=S△AFM+S△AMD=
S△AFD,
在Rt△AFD中,
AF=AD·cos∠FAD=12×cos 60°=6,
DF=AD·sin∠FAD=12×sin 60°=6,
∴S△AFD=×6×6=18,
∴S△AFM+S△CDM=18.
