第一章 直角三角形的边角关系 评估测试卷(含答案) 2024-2025学年数学北师大版九年级下册
文档属性
| 名称 | 第一章 直角三角形的边角关系 评估测试卷(含答案) 2024-2025学年数学北师大版九年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 236.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-26 21:27:41 | ||
图片预览



文档简介
第一章 直角三角形的边角关系 评估测试卷
(满分:120分 时间:120分钟)
一、选择题(本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(2024天津河北区二模)计算cos 30°的值是 ( )
A. B.1 C. D.3
2.若tan A=0.189 0,利用科学计算器计算∠A的度数,下列按键顺序正确的是 ( )
A.SHIFT tan 0 . 1 8 9 0 =
B.SHIFT 0 . 1 8 9 0 tan =
C.0 . 1 8 9 0 tan SHIFT =
D.tan 0 . 1 8 9 0 SHIFT =
3.如图,在△ABC中,∠C=90°,BC=a,AC=b,AB=c,则下列选项正确的是 ( )
A.sin A= B.cos B=
C.tan A= D.tan B=
4.(2024石家庄新华区模拟)在△ABC中,∠C=90°,若tan A=,则cos B的值为 ( )
A. B. C. D.
5.如图,在△ABC中,AB=AC=5,sin B=,则BC的长是 ( )
A.3 B.6
C.8 D.9
6.在△ABC中,若+=0,则∠C的度数是 ( )
A.120° B.105°
C.75° D.45°
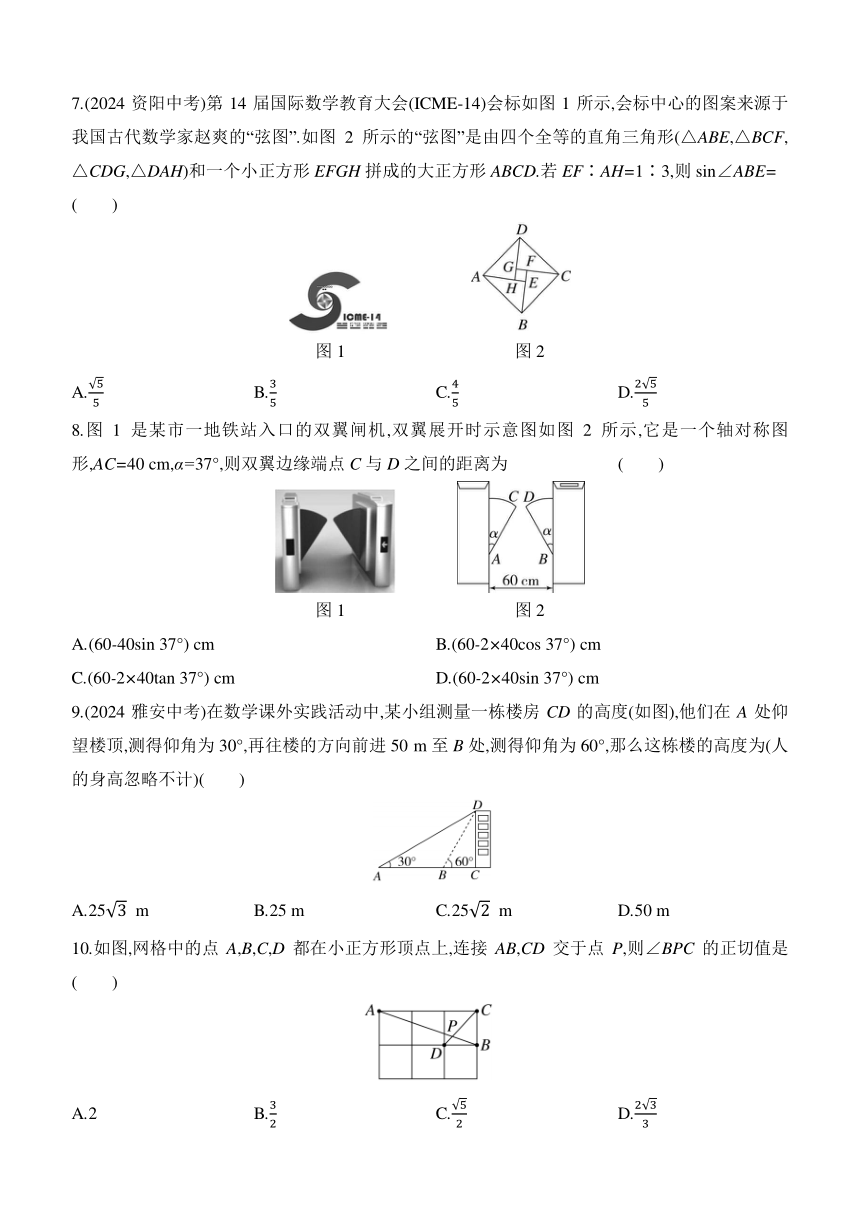
7.(2024资阳中考)第14届国际数学教育大会(ICME-14)会标如图1所示,会标中心的图案来源于我国古代数学家赵爽的“弦图”.如图2所示的“弦图”是由四个全等的直角三角形(△ABE,△BCF,△CDG,△DAH)和一个小正方形EFGH拼成的大正方形ABCD.若EF∶AH=1∶3,则sin∠ABE=
( )
图1 图2
A. B. C. D.
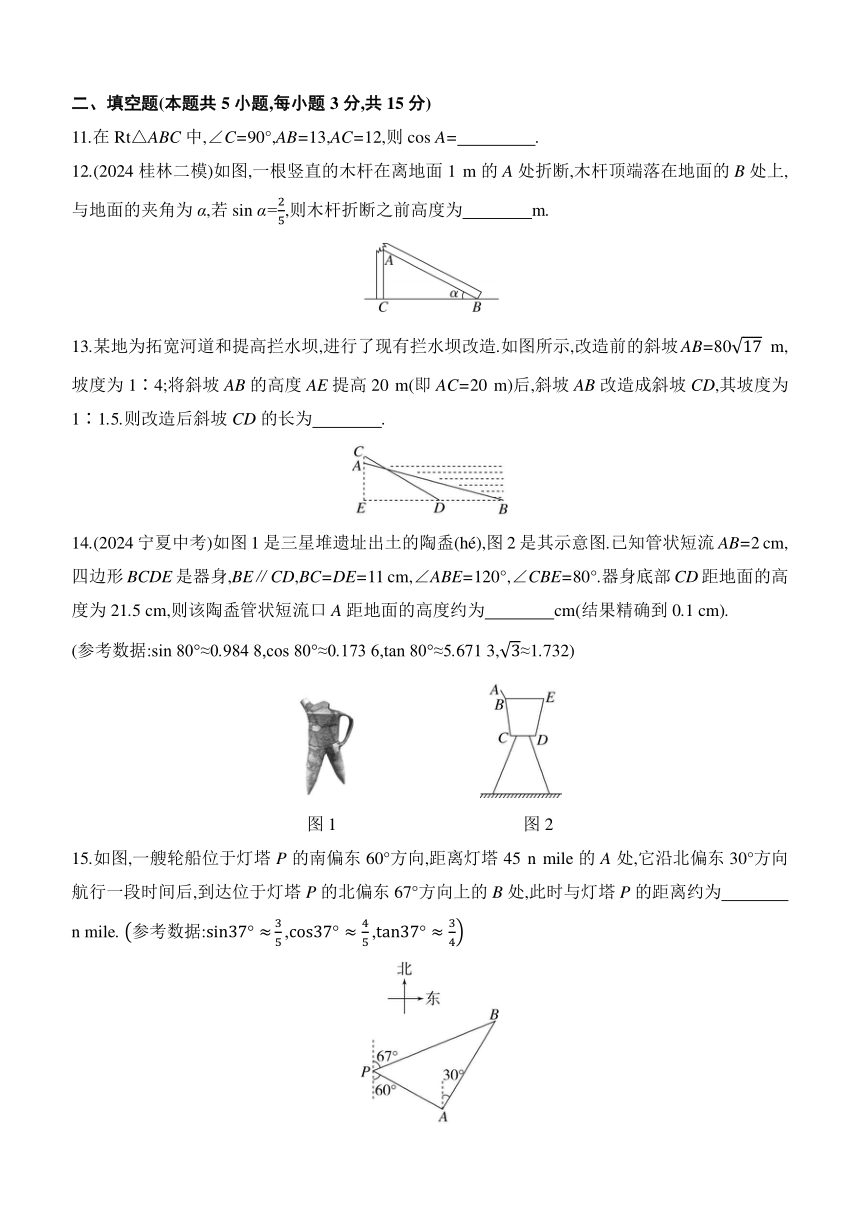
8.图1是某市一地铁站入口的双翼闸机,双翼展开时示意图如图2所示,它是一个轴对称图形,AC=40 cm,α=37°,则双翼边缘端点C与D之间的距离为 ( )
图1 图2
A.(60-40sin 37°) cm B.(60-2×40cos 37°) cm
C.(60-2×40tan 37°) cm D.(60-2×40sin 37°) cm
9.(2024雅安中考)在数学课外实践活动中,某小组测量一栋楼房CD的高度(如图),他们在A处仰望楼顶,测得仰角为30°,再往楼的方向前进50 m至B处,测得仰角为60°,那么这栋楼的高度为(人的身高忽略不计)( )
A.25 m B.25 m C.25 m D.50 m
10.如图,网格中的点A,B,C,D都在小正方形顶点上,连接AB,CD交于点P,则∠BPC的正切值是( )
A.2 B. C. D.
二、填空题(本题共5小题,每小题3分,共15分)
11.在Rt△ABC中,∠C=90°,AB=13,AC=12,则cos A= .
12.(2024桂林二模)如图,一根竖直的木杆在离地面1 m的A处折断,木杆顶端落在地面的B处上,与地面的夹角为α,若sin α=,则木杆折断之前高度为 m.
13.某地为拓宽河道和提高拦水坝,进行了现有拦水坝改造.如图所示,改造前的斜坡AB=80 m,坡度为1∶4;将斜坡AB的高度AE提高20 m(即AC=20 m)后,斜坡AB改造成斜坡CD,其坡度为1∶1.5.则改造后斜坡CD的长为 .
14.(2024宁夏中考)如图1是三星堆遗址出土的陶盉(hé),图2是其示意图.已知管状短流AB=2 cm,四边形BCDE是器身,BE∥CD,BC=DE=11 cm,∠ABE=120°,∠CBE=80°.器身底部CD距地面的高度为21.5 cm,则该陶盉管状短流口A距地面的高度约为 cm(结果精确到0.1 cm).
(参考数据:sin 80°≈0.984 8,cos 80°≈0.173 6,tan 80°≈5.671 3,≈1.732)
图1 图2
15.如图,一艘轮船位于灯塔P的南偏东60°方向,距离灯塔45 n mile的A处,它沿北偏东30°方向航行一段时间后,到达位于灯塔P的北偏东67°方向上的B处,此时与灯塔P的距离约为
n mile.
三、解答题(本题共8小题,共75分.解答应写出文字说明、演算步骤或推理过程)
16.(6分)计算:
(1)sin230°+2sin 60°+tan 45°+cos230°;
(2)-2sin 45°+2cos 60°+|1-|+-1.
17.(6分)在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边.
(1)已知c=2,b=,求∠B;
(2)已知c=12,sin A=,求b.
18.(8分)(2024浙江中考)如图,在△ABC中,AD⊥BC,AE是BC边上的中线,AB=10,AD=6,tan∠ACB
=1.
(1)求BC的长;
(2)求sin∠DAE的值.
19.(10分)(2024辽宁中考)如图1,在水平地面上,一辆小车用一根绕过定滑轮的绳子将物体竖直向上提起.起始位置示意图如图2,此时测得点A到BC所在直线的距离AC=3 m,∠CAB=60°,停止位置示意图如图3,此时测得∠CDB=37°(点C,A,D在同一直线上,且直线CD与地面平行),图3中所有点在同一平面内.定滑轮半径忽略不计,运动过程中绳子总长不变.
图1 图2 图3
(1)求AB的长;
(2)求物体上升的高度CE(结果精确到0.1 m).
(参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75,≈1.73)
20.(10分)如图,某海域有两灯塔A,B,其中灯塔B在灯塔A的南偏东30°方向,且A,B相距
n mile.一渔船在C处捕鱼,测得C处在灯塔A的北偏东30°方向、灯塔B的正北方向.
(1)求B,C两处的距离;
(2)该渔船从C处沿北偏东65°方向航行一段时间后,突发故障滞留于D处,并发出求救信号.此时,在灯塔B处的渔政船测得D处在北偏东27°方向,便立即以18 n mile/h的速度沿BD方向航行至D处救援,求渔政船的航行时间.
(注:点A,B,C,D在同一水平面内;参考数据:tan 65°≈2.1,tan 27°≈0.5)
21.(10分)(2024巴中中考)某兴趣小组开展了测量电线塔高度的实践活动.如图所示,斜坡BE的坡度i=1∶,BE=6 m,在B处测得电线塔CD顶部D的仰角为45°,在E处测得电线塔CD顶部D的仰角为60°.
(1)求点B离水平地面的高度AB;
(2)求电线塔CD的高度(结果保留根号).
22.(12分)如图,某路段路旁有一盏路灯,灯杆AB的正前方有一斜坡CD,已知斜坡CD的长为4 m,坡度i=1∶,坡角为∠DCF,灯光受灯罩的影响,最远端的光线BE与地面的夹角∠BEF为28°,最近端的光线BC恰好与地面交于坡面的底端C处,且与地面的夹角∠BCF为60°,AD=1 m,点A,B,C,D,E,F在同一平面上.
(1)求灯杆AB的高度(结果保留根号);
(2)求CE的长(结果精确到0.1 m,参考数据:sin 28°≈0.47,cos 28°≈0.88,tan 28°≈0.53,≈1.73).
23.(13分)如图是房屋的侧面示意图,它是一个轴对称图形,对称轴是房屋的高AB所在的直线,为了测量房屋的高度,在地面上点C测得屋顶A的仰角为30°,此时地面上点C、屋檐上点E、屋顶上点A三点恰好在同一条直线上,继续向房屋方向走8 m到达点D时,又测得屋檐点E的仰角为63.5°,房屋的顶层横梁EF=12 m,EF∥CB,AB交EF于点G(点C,D,B在同一水平线上).
(1)求屋顶到横梁的距离AG(结果精确到0.1 m);
(2)求房屋的高AB(结果精确到1 m).
(参考数据:sin 63.5°≈0.89,cos 63.5°≈0.45,tan 63.5°≈2.00,≈1.73)
【详解答案】
1.C 解析:cos 30°=.故选C.
2.A 解析:∵tan A=0.189 0,∴利用科学计算器求∠A的度数,按键顺序为选项A.故选A.
3.D 解析:在△ABC中,∠C=90°,BC=a,AC=b,AB=c,∴sin A=,cos B=,tan A=,tan B=.故选D.
4.D 解析:∵∠C=90°,tan A=,∴,设BC=x,AC=3x,故AB=x,则cos B=.故选D.
5.B 解析:如图,过点A作BC的垂线,垂足为M,在Rt△ABM中,sin B=,∴AM=AB·sin B=5×=4,∴BM==3.
又∵AB=AC,∴BC=2BM=6.故选B.
6.A 解析:∵sin A-+=0,∴sin A-=0,-cos B=0,∴sin A=,cos B=,∴∠A=30°,∠B=30°,
∴∠C=180°-∠A-∠B=120°.故选A.
7.C 解析:根据题意,设EF=x,则AH=3x,∵△ABE≌△DAH,四边形EFGH为正方形,∴BE=AH=3x,HE=EF=x,
∴AE=4x,∵∠AEB=90°,∴AB==5x,∴sin∠ABE=.故选C.
8.D 解析:如图,作直线CD,交双翼闸机于点E,F,则CE⊥AE,DF⊥BF,
由题意可得CE=DF,EF=60 cm,在Rt△ACE中,CE=AC·sin 37°=40sin 37°(cm),∴CD=EF-2CE=(60-2×40sin 37°)cm.故选D.
9.A 解析:设DC=x m,在Rt△ACD中,∠A=30°,tan A=,即tan 30°=,整理得:AC=x m,在Rt△BCD中,∠DBC=60°,tan∠DBC=,即tan 60°=,整理得:BC=x m.∵AB=50 m,∴AC-BC=50,即x-x=50,解得x=25,则这栋楼的高度为25 m.故选A.
10.A 解析:作BE∥CD,如图所示,∵BE∥CD,∴∠BPC=∠ABE.设小正方形的边长为a,由图可得,AB=a,AE==2a,BE=a,∴AB2=AE2+BE2,∴△AEB是直角三角形,∴tan∠ABE==2,∴tan∠BPC=2.故选A.
11. 解析:cos A=.
12.3.5 解析:在Rt△ABC中,AC=1 m,∠B=α,
∵sin α=,∴AB=2.5,
∴木杆折断之前高度为AC+AB=1+2.5=3.5(m).
13.50 m 解析:在Rt△ABE中,AB=80 m,,∴设AE=x m,BE=4x m,∴AB=x=80,∴x=80,∴AE=80 m,∴CE=AE+AC=100(m),∵斜坡CD的坡度为1∶1.5,∴DE=150 m,由勾股定理得:CD==50 m,∴斜坡CD的长为50 m.
14.34.1 解析:如图,过点C作CF⊥BE,垂足为F,过点A作AG⊥EB,交EB的延长线于点G,∵∠ABE=120°,
∴∠ABG=180°-∠ABE=60°,在Rt△ABG中,AB=2 cm,∴AG=AB·sin 60°=2×(cm),在Rt△BCF中,
∠CBE=80°,BC=11 cm,∴CF=BC·sin 80°≈11×0.984 8=10.832 8(cm).∵器身底部CD距地面的高度为21.5 cm,
∴该陶盉管状短流口A距地面的高度=AG+CF+21.5=+10.832 8+21.5≈34.1(cm),∴该陶盉管状短流口A距地面的高度约为34.1 cm.
15.75 解析:如图所示标注字母,
根据题意得,∠CAP=∠EPA=60°,∠CAB=30°,PA=45 n mile,∴∠PAB=90°,∠APB=180°-67°-60°=53°,∴∠B=180°-90°-53°=37°,在Rt△PAB中,sin 37°=,PB=≈=75(n mile),即此时B与灯塔P的距离约为75 n mile.
16.解:(1)原式=+2×+1++1+=2+.
(2)原式=-2×+2×-1+(2-1)-1
=2-+1+-1+2
=2+2.
17.解:(1)∵sin B=,
∴∠B=45°.
(2)∵c=12,sin A=,
∴a=4,
∴b==8.
18.解:(1)∵AD⊥BC,AB=10,AD=6,
∴BD==8.
∵tan∠ACB=1,
∴CD=AD=6,
∴BC=BD+CD=8+6=14.
(2)∵AE是BC边上的中线,
∴CE=BC=7,
∴DE=CE-CD=7-6=1.
∵AD⊥BC,
∴AE=,
∴sin∠DAE=.
19.解:(1)在Rt△ABC中,AC=3 m,
∠CAB=60°,
∴∠ABC=30°,
∴AB=2AC=6 m,
则AB的长为6 m.
(2)在Rt△ABC中,AB=6 m,AC=3 m,
根据勾股定理得:BC==3(m),
在Rt△BCD中,∠CDB=37°,
∴sin∠CDB=,即≈0.60,
∴BD≈8.65 m,
∴CE=BD-BA=8.65-6=2.65≈2.7(m),
则物体上升的高度CE约为2.7 m.
20.解:(1)由题意得,∠ACB=∠ABC=30°,
∴AC=AB= n mile.
如图,过点A作AH⊥BC于点H,
∴∠AHC=∠AHB=90°,CH=BH,
∴CH=BH=AB==8(n mile),
∴BC=16 n mile.
答:B,C两处的距离为16 n mile.
(2)如图,过点D作DG⊥BC交BC的延长线于点G,
在Rt△BDG中,BG=≈=2DG,
在Rt△CDG中,CG=≈.
∵BC=BG-CG,
∴2DG-=16,
∴DG=10.5 n mile,
∴CG=5 n mile,
∴BG=BC+CG=21 n mile,
∴BD= n mile,
∴渔政船的航行时间为÷18=(h).
21.解:(1)由题意得:BA⊥AE,
∵斜坡BE的坡度i=1∶,
∴,
在Rt△ABE中,tan∠BEA=,
∴∠BEA=30°.
∵BE=6 m,
∴AB=BE=3 m,AE=AB=3 m,
∴点B离水平地面的高度AB为3 m.
(2)如图,过点B作BF⊥CD,垂足为F,
由题意得:CF=AB=3 m,BF=AC,
设EC=x m,
∵AE=3 m,
∴BF=AC=AE+CE=(x+3)m,
在Rt△CDE中,∠DEC=60°,
∴CD=CE·tan 60°=x(m),
在Rt△BDF中,∠DBF=45°,
∴DF=BF·tan 45°=(x+3)m.
∵DF+CF=CD,
∴x+3+3=x,
解得:x=6+3,
∴CD=x=(6+9)m,
∴电线塔CD的高度为(6+9)m.
22.解:(1)如图,延长BA交CF于点H,过点D作DG⊥CF于点G,
则四边形DGHA为矩形,
∴GH=AD=1 m,DG=AH.
∵斜坡CD的坡度i=1∶,
∴tan∠DCF=,
∴∠DCF=30°,
∴DG=CD=2 m,
由勾股定理得:CG==2(m),
∴CH=CG+GH=(2+1)m,
在Rt△BCH中,∠BCH=60°,
∵tan∠BCH=,
∴BH=CH·tan∠BCH=(2+1)×=(6+)(m),
∴AB=BH-AH=6+-2=(4+)(m).
答:灯杆AB的高度为(4+)m.
(2)在Rt△BEH中,∠BEH=28°,
∵tan∠BEH=,
∴EH=≈14.58(m),
∴CE=EH-CH=14.58-(2+1)≈10.1(m).
答:CE的长约为10.1 m.
23.解:(1)∵房屋的侧面示意图,它是一个轴对称图形,对称轴是房屋的高AB所在的直线,
EF∥BC,
∴AG⊥EF,EG=FG=EF=×12=6(m),∠AEG=∠ACB=30°,
在Rt△AGE中,∠AGE=90°,∠AEG=30°,EG=6,
∵tan∠AEG=,
∴AG=EG·tan∠AEG=6×tan 30°=6×≈2×1.73=3.46≈3.5(m).
答:屋顶到横梁的距离AG约为3.5 m.
(2)如图,过点E作EH⊥CB于点H,设EH=x m,
在Rt△EDH中,∠EHD=90°,
∠EDH=63.5°,
∵tan∠EDH=,
∴DH=≈(m),
在Rt△ECH中,∠EHC=90°,
∠ECH=30°,
∴tan∠ECH=,
∴CH=x m.
∵CH-DH=CD=8 m,∴x-=8,
1.73x-0.5x=8,
解得x≈6.5.
∵四边形EHBG为矩形,
∴BG=EH=6.5 m,
∴AB=AG+BG=3.46+6.5=9.96≈10(m).
答:房屋的高AB约为10 m.
(满分:120分 时间:120分钟)
一、选择题(本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(2024天津河北区二模)计算cos 30°的值是 ( )
A. B.1 C. D.3
2.若tan A=0.189 0,利用科学计算器计算∠A的度数,下列按键顺序正确的是 ( )
A.SHIFT tan 0 . 1 8 9 0 =
B.SHIFT 0 . 1 8 9 0 tan =
C.0 . 1 8 9 0 tan SHIFT =
D.tan 0 . 1 8 9 0 SHIFT =
3.如图,在△ABC中,∠C=90°,BC=a,AC=b,AB=c,则下列选项正确的是 ( )
A.sin A= B.cos B=
C.tan A= D.tan B=
4.(2024石家庄新华区模拟)在△ABC中,∠C=90°,若tan A=,则cos B的值为 ( )
A. B. C. D.
5.如图,在△ABC中,AB=AC=5,sin B=,则BC的长是 ( )
A.3 B.6
C.8 D.9
6.在△ABC中,若+=0,则∠C的度数是 ( )
A.120° B.105°
C.75° D.45°
7.(2024资阳中考)第14届国际数学教育大会(ICME-14)会标如图1所示,会标中心的图案来源于我国古代数学家赵爽的“弦图”.如图2所示的“弦图”是由四个全等的直角三角形(△ABE,△BCF,△CDG,△DAH)和一个小正方形EFGH拼成的大正方形ABCD.若EF∶AH=1∶3,则sin∠ABE=
( )
图1 图2
A. B. C. D.
8.图1是某市一地铁站入口的双翼闸机,双翼展开时示意图如图2所示,它是一个轴对称图形,AC=40 cm,α=37°,则双翼边缘端点C与D之间的距离为 ( )
图1 图2
A.(60-40sin 37°) cm B.(60-2×40cos 37°) cm
C.(60-2×40tan 37°) cm D.(60-2×40sin 37°) cm
9.(2024雅安中考)在数学课外实践活动中,某小组测量一栋楼房CD的高度(如图),他们在A处仰望楼顶,测得仰角为30°,再往楼的方向前进50 m至B处,测得仰角为60°,那么这栋楼的高度为(人的身高忽略不计)( )
A.25 m B.25 m C.25 m D.50 m
10.如图,网格中的点A,B,C,D都在小正方形顶点上,连接AB,CD交于点P,则∠BPC的正切值是( )
A.2 B. C. D.
二、填空题(本题共5小题,每小题3分,共15分)
11.在Rt△ABC中,∠C=90°,AB=13,AC=12,则cos A= .
12.(2024桂林二模)如图,一根竖直的木杆在离地面1 m的A处折断,木杆顶端落在地面的B处上,与地面的夹角为α,若sin α=,则木杆折断之前高度为 m.
13.某地为拓宽河道和提高拦水坝,进行了现有拦水坝改造.如图所示,改造前的斜坡AB=80 m,坡度为1∶4;将斜坡AB的高度AE提高20 m(即AC=20 m)后,斜坡AB改造成斜坡CD,其坡度为1∶1.5.则改造后斜坡CD的长为 .
14.(2024宁夏中考)如图1是三星堆遗址出土的陶盉(hé),图2是其示意图.已知管状短流AB=2 cm,四边形BCDE是器身,BE∥CD,BC=DE=11 cm,∠ABE=120°,∠CBE=80°.器身底部CD距地面的高度为21.5 cm,则该陶盉管状短流口A距地面的高度约为 cm(结果精确到0.1 cm).
(参考数据:sin 80°≈0.984 8,cos 80°≈0.173 6,tan 80°≈5.671 3,≈1.732)
图1 图2
15.如图,一艘轮船位于灯塔P的南偏东60°方向,距离灯塔45 n mile的A处,它沿北偏东30°方向航行一段时间后,到达位于灯塔P的北偏东67°方向上的B处,此时与灯塔P的距离约为
n mile.
三、解答题(本题共8小题,共75分.解答应写出文字说明、演算步骤或推理过程)
16.(6分)计算:
(1)sin230°+2sin 60°+tan 45°+cos230°;
(2)-2sin 45°+2cos 60°+|1-|+-1.
17.(6分)在Rt△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边.
(1)已知c=2,b=,求∠B;
(2)已知c=12,sin A=,求b.
18.(8分)(2024浙江中考)如图,在△ABC中,AD⊥BC,AE是BC边上的中线,AB=10,AD=6,tan∠ACB
=1.
(1)求BC的长;
(2)求sin∠DAE的值.
19.(10分)(2024辽宁中考)如图1,在水平地面上,一辆小车用一根绕过定滑轮的绳子将物体竖直向上提起.起始位置示意图如图2,此时测得点A到BC所在直线的距离AC=3 m,∠CAB=60°,停止位置示意图如图3,此时测得∠CDB=37°(点C,A,D在同一直线上,且直线CD与地面平行),图3中所有点在同一平面内.定滑轮半径忽略不计,运动过程中绳子总长不变.
图1 图2 图3
(1)求AB的长;
(2)求物体上升的高度CE(结果精确到0.1 m).
(参考数据:sin 37°≈0.60,cos 37°≈0.80,tan 37°≈0.75,≈1.73)
20.(10分)如图,某海域有两灯塔A,B,其中灯塔B在灯塔A的南偏东30°方向,且A,B相距
n mile.一渔船在C处捕鱼,测得C处在灯塔A的北偏东30°方向、灯塔B的正北方向.
(1)求B,C两处的距离;
(2)该渔船从C处沿北偏东65°方向航行一段时间后,突发故障滞留于D处,并发出求救信号.此时,在灯塔B处的渔政船测得D处在北偏东27°方向,便立即以18 n mile/h的速度沿BD方向航行至D处救援,求渔政船的航行时间.
(注:点A,B,C,D在同一水平面内;参考数据:tan 65°≈2.1,tan 27°≈0.5)
21.(10分)(2024巴中中考)某兴趣小组开展了测量电线塔高度的实践活动.如图所示,斜坡BE的坡度i=1∶,BE=6 m,在B处测得电线塔CD顶部D的仰角为45°,在E处测得电线塔CD顶部D的仰角为60°.
(1)求点B离水平地面的高度AB;
(2)求电线塔CD的高度(结果保留根号).
22.(12分)如图,某路段路旁有一盏路灯,灯杆AB的正前方有一斜坡CD,已知斜坡CD的长为4 m,坡度i=1∶,坡角为∠DCF,灯光受灯罩的影响,最远端的光线BE与地面的夹角∠BEF为28°,最近端的光线BC恰好与地面交于坡面的底端C处,且与地面的夹角∠BCF为60°,AD=1 m,点A,B,C,D,E,F在同一平面上.
(1)求灯杆AB的高度(结果保留根号);
(2)求CE的长(结果精确到0.1 m,参考数据:sin 28°≈0.47,cos 28°≈0.88,tan 28°≈0.53,≈1.73).
23.(13分)如图是房屋的侧面示意图,它是一个轴对称图形,对称轴是房屋的高AB所在的直线,为了测量房屋的高度,在地面上点C测得屋顶A的仰角为30°,此时地面上点C、屋檐上点E、屋顶上点A三点恰好在同一条直线上,继续向房屋方向走8 m到达点D时,又测得屋檐点E的仰角为63.5°,房屋的顶层横梁EF=12 m,EF∥CB,AB交EF于点G(点C,D,B在同一水平线上).
(1)求屋顶到横梁的距离AG(结果精确到0.1 m);
(2)求房屋的高AB(结果精确到1 m).
(参考数据:sin 63.5°≈0.89,cos 63.5°≈0.45,tan 63.5°≈2.00,≈1.73)
【详解答案】
1.C 解析:cos 30°=.故选C.
2.A 解析:∵tan A=0.189 0,∴利用科学计算器求∠A的度数,按键顺序为选项A.故选A.
3.D 解析:在△ABC中,∠C=90°,BC=a,AC=b,AB=c,∴sin A=,cos B=,tan A=,tan B=.故选D.
4.D 解析:∵∠C=90°,tan A=,∴,设BC=x,AC=3x,故AB=x,则cos B=.故选D.
5.B 解析:如图,过点A作BC的垂线,垂足为M,在Rt△ABM中,sin B=,∴AM=AB·sin B=5×=4,∴BM==3.
又∵AB=AC,∴BC=2BM=6.故选B.
6.A 解析:∵sin A-+=0,∴sin A-=0,-cos B=0,∴sin A=,cos B=,∴∠A=30°,∠B=30°,
∴∠C=180°-∠A-∠B=120°.故选A.
7.C 解析:根据题意,设EF=x,则AH=3x,∵△ABE≌△DAH,四边形EFGH为正方形,∴BE=AH=3x,HE=EF=x,
∴AE=4x,∵∠AEB=90°,∴AB==5x,∴sin∠ABE=.故选C.
8.D 解析:如图,作直线CD,交双翼闸机于点E,F,则CE⊥AE,DF⊥BF,
由题意可得CE=DF,EF=60 cm,在Rt△ACE中,CE=AC·sin 37°=40sin 37°(cm),∴CD=EF-2CE=(60-2×40sin 37°)cm.故选D.
9.A 解析:设DC=x m,在Rt△ACD中,∠A=30°,tan A=,即tan 30°=,整理得:AC=x m,在Rt△BCD中,∠DBC=60°,tan∠DBC=,即tan 60°=,整理得:BC=x m.∵AB=50 m,∴AC-BC=50,即x-x=50,解得x=25,则这栋楼的高度为25 m.故选A.
10.A 解析:作BE∥CD,如图所示,∵BE∥CD,∴∠BPC=∠ABE.设小正方形的边长为a,由图可得,AB=a,AE==2a,BE=a,∴AB2=AE2+BE2,∴△AEB是直角三角形,∴tan∠ABE==2,∴tan∠BPC=2.故选A.
11. 解析:cos A=.
12.3.5 解析:在Rt△ABC中,AC=1 m,∠B=α,
∵sin α=,∴AB=2.5,
∴木杆折断之前高度为AC+AB=1+2.5=3.5(m).
13.50 m 解析:在Rt△ABE中,AB=80 m,,∴设AE=x m,BE=4x m,∴AB=x=80,∴x=80,∴AE=80 m,∴CE=AE+AC=100(m),∵斜坡CD的坡度为1∶1.5,∴DE=150 m,由勾股定理得:CD==50 m,∴斜坡CD的长为50 m.
14.34.1 解析:如图,过点C作CF⊥BE,垂足为F,过点A作AG⊥EB,交EB的延长线于点G,∵∠ABE=120°,
∴∠ABG=180°-∠ABE=60°,在Rt△ABG中,AB=2 cm,∴AG=AB·sin 60°=2×(cm),在Rt△BCF中,
∠CBE=80°,BC=11 cm,∴CF=BC·sin 80°≈11×0.984 8=10.832 8(cm).∵器身底部CD距地面的高度为21.5 cm,
∴该陶盉管状短流口A距地面的高度=AG+CF+21.5=+10.832 8+21.5≈34.1(cm),∴该陶盉管状短流口A距地面的高度约为34.1 cm.
15.75 解析:如图所示标注字母,
根据题意得,∠CAP=∠EPA=60°,∠CAB=30°,PA=45 n mile,∴∠PAB=90°,∠APB=180°-67°-60°=53°,∴∠B=180°-90°-53°=37°,在Rt△PAB中,sin 37°=,PB=≈=75(n mile),即此时B与灯塔P的距离约为75 n mile.
16.解:(1)原式=+2×+1++1+=2+.
(2)原式=-2×+2×-1+(2-1)-1
=2-+1+-1+2
=2+2.
17.解:(1)∵sin B=,
∴∠B=45°.
(2)∵c=12,sin A=,
∴a=4,
∴b==8.
18.解:(1)∵AD⊥BC,AB=10,AD=6,
∴BD==8.
∵tan∠ACB=1,
∴CD=AD=6,
∴BC=BD+CD=8+6=14.
(2)∵AE是BC边上的中线,
∴CE=BC=7,
∴DE=CE-CD=7-6=1.
∵AD⊥BC,
∴AE=,
∴sin∠DAE=.
19.解:(1)在Rt△ABC中,AC=3 m,
∠CAB=60°,
∴∠ABC=30°,
∴AB=2AC=6 m,
则AB的长为6 m.
(2)在Rt△ABC中,AB=6 m,AC=3 m,
根据勾股定理得:BC==3(m),
在Rt△BCD中,∠CDB=37°,
∴sin∠CDB=,即≈0.60,
∴BD≈8.65 m,
∴CE=BD-BA=8.65-6=2.65≈2.7(m),
则物体上升的高度CE约为2.7 m.
20.解:(1)由题意得,∠ACB=∠ABC=30°,
∴AC=AB= n mile.
如图,过点A作AH⊥BC于点H,
∴∠AHC=∠AHB=90°,CH=BH,
∴CH=BH=AB==8(n mile),
∴BC=16 n mile.
答:B,C两处的距离为16 n mile.
(2)如图,过点D作DG⊥BC交BC的延长线于点G,
在Rt△BDG中,BG=≈=2DG,
在Rt△CDG中,CG=≈.
∵BC=BG-CG,
∴2DG-=16,
∴DG=10.5 n mile,
∴CG=5 n mile,
∴BG=BC+CG=21 n mile,
∴BD= n mile,
∴渔政船的航行时间为÷18=(h).
21.解:(1)由题意得:BA⊥AE,
∵斜坡BE的坡度i=1∶,
∴,
在Rt△ABE中,tan∠BEA=,
∴∠BEA=30°.
∵BE=6 m,
∴AB=BE=3 m,AE=AB=3 m,
∴点B离水平地面的高度AB为3 m.
(2)如图,过点B作BF⊥CD,垂足为F,
由题意得:CF=AB=3 m,BF=AC,
设EC=x m,
∵AE=3 m,
∴BF=AC=AE+CE=(x+3)m,
在Rt△CDE中,∠DEC=60°,
∴CD=CE·tan 60°=x(m),
在Rt△BDF中,∠DBF=45°,
∴DF=BF·tan 45°=(x+3)m.
∵DF+CF=CD,
∴x+3+3=x,
解得:x=6+3,
∴CD=x=(6+9)m,
∴电线塔CD的高度为(6+9)m.
22.解:(1)如图,延长BA交CF于点H,过点D作DG⊥CF于点G,
则四边形DGHA为矩形,
∴GH=AD=1 m,DG=AH.
∵斜坡CD的坡度i=1∶,
∴tan∠DCF=,
∴∠DCF=30°,
∴DG=CD=2 m,
由勾股定理得:CG==2(m),
∴CH=CG+GH=(2+1)m,
在Rt△BCH中,∠BCH=60°,
∵tan∠BCH=,
∴BH=CH·tan∠BCH=(2+1)×=(6+)(m),
∴AB=BH-AH=6+-2=(4+)(m).
答:灯杆AB的高度为(4+)m.
(2)在Rt△BEH中,∠BEH=28°,
∵tan∠BEH=,
∴EH=≈14.58(m),
∴CE=EH-CH=14.58-(2+1)≈10.1(m).
答:CE的长约为10.1 m.
23.解:(1)∵房屋的侧面示意图,它是一个轴对称图形,对称轴是房屋的高AB所在的直线,
EF∥BC,
∴AG⊥EF,EG=FG=EF=×12=6(m),∠AEG=∠ACB=30°,
在Rt△AGE中,∠AGE=90°,∠AEG=30°,EG=6,
∵tan∠AEG=,
∴AG=EG·tan∠AEG=6×tan 30°=6×≈2×1.73=3.46≈3.5(m).
答:屋顶到横梁的距离AG约为3.5 m.
(2)如图,过点E作EH⊥CB于点H,设EH=x m,
在Rt△EDH中,∠EHD=90°,
∠EDH=63.5°,
∵tan∠EDH=,
∴DH=≈(m),
在Rt△ECH中,∠EHC=90°,
∠ECH=30°,
∴tan∠ECH=,
∴CH=x m.
∵CH-DH=CD=8 m,∴x-=8,
1.73x-0.5x=8,
解得x≈6.5.
∵四边形EHBG为矩形,
∴BG=EH=6.5 m,
∴AB=AG+BG=3.46+6.5=9.96≈10(m).
答:房屋的高AB约为10 m.
