期末评估测试卷(含答案) 2024-2025学年数学北师大版九年级下册
文档属性
| 名称 | 期末评估测试卷(含答案) 2024-2025学年数学北师大版九年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 398.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-26 21:27:50 | ||
图片预览




文档简介
期末评估测试卷
(满分:120分 时间:120分钟)
一、选择题(本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(2024武威凉州区一模)如图所示,△ABC的顶点是正方形网格的格点,则sin A的值为 ( )
A. B. C. D.
2.二次函数y=ax2+bx的图象如图所示,则一次函数y=ax+b的图象不经过 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.如图,一辆自行车竖直摆放在水平地面上,右边是它的部分示意图,现测得∠A=88°,∠C=42°,
AB=60,则点A到BC的距离为 ( )
A.60sin 50° B. C.60cos 50° D.60tan 50°
4.数学来源于生活,伞是生活中常见的一种工具,撑开后如图1所示,由此发现数学知识——抛物线.如图2,以伞柄所在的直线为y轴,以伞骨OA,OB的交点O为坐标原点建立平面直角坐标系.点C为抛物线的顶点,点A,B在抛物线上,OA,OB关于y轴对称.抛物线的表达式为y=-0.1x2+1,若点A到x轴的距离是0.6 dm,则A,B两点之间的距离是 ( )
图1 图2
A.4 dm B.6 dm C.8 dm D.10 dm
5.(2024赤峰中考)如图,AD是☉O的直径,AB是☉O的弦,半径OC⊥AB,连接CD,交OB于点E,
∠BOC=42°,则∠OED的度数是 ( )
A.61° B.63° C.65° D.67°
6.如图,分别延长圆内接四边形ABCD的两组对边,延长线分别相交于点E,F.若∠E=54°41',
∠F=43°19',则∠A的度数为 ( )
A.42° B.41°20' C.41° D.40°20'
7.如图,边长为2的正六边形ABCDEF内接于☉O,则它的内切圆半径为 ( )
A.1 B.2 C. D.
8.(2024泰安中考)两个半径相等的半圆按如图方式放置,半圆O'的一个直径端点与半圆O的圆心重合,若半圆的半径为2,则阴影部分的面积是 ( )
A.π- B.π C.π- D.π-
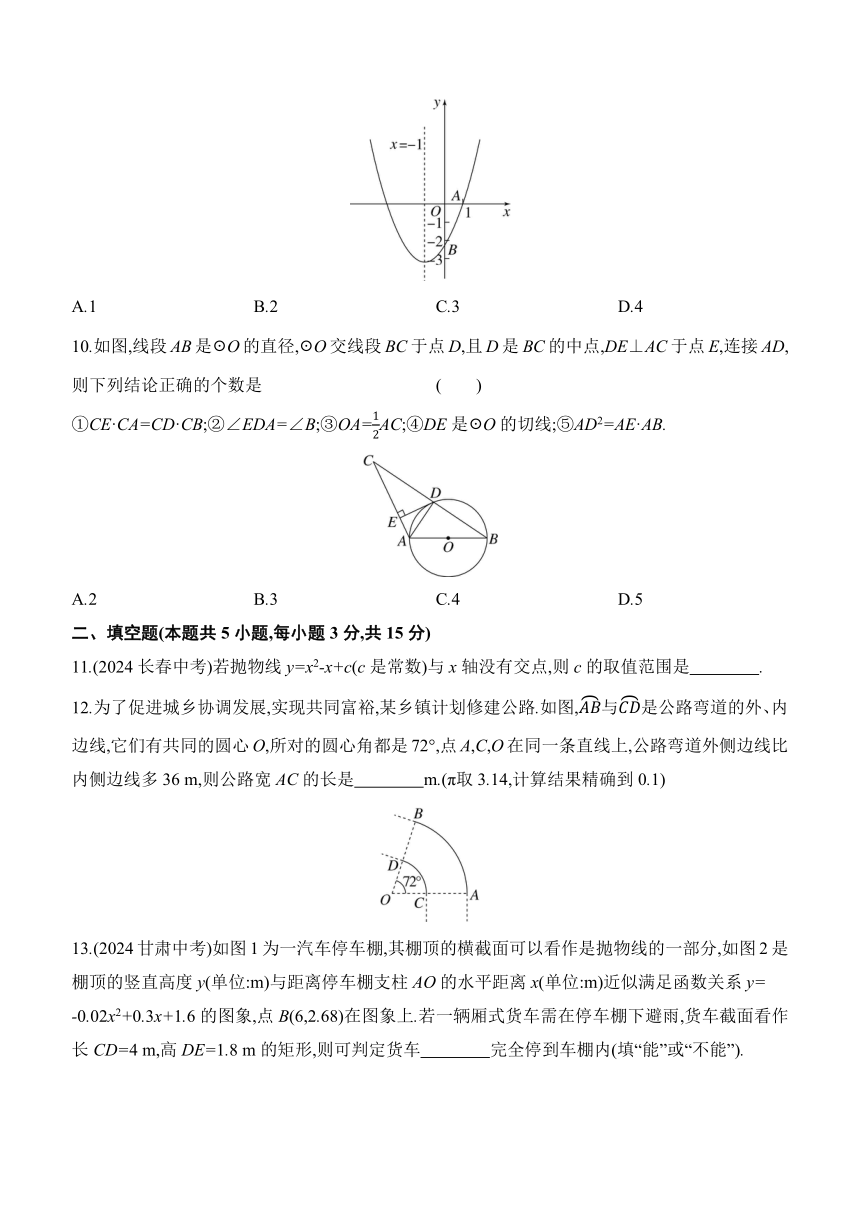
9.(2024遂宁中考)如图,已知抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)的对称轴为直线x=-1,且该抛物线与x轴交于点A(1,0),与y轴的交点B在(0,-2),(0,-3)之间(不含端点),则下列结论正确的个数是 ( )
①abc>0;②9a-3b+c>0;③A.1 B.2 C.3 D.4
10.如图,线段AB是☉O的直径,☉O交线段BC于点D,且D是BC的中点,DE⊥AC于点E,连接AD,则下列结论正确的个数是 ( )
①CE·CA=CD·CB;②∠EDA=∠B;③OA=AC;④DE是☉O的切线;⑤AD2=AE·AB.
A.2 B.3 C.4 D.5
二、填空题(本题共5小题,每小题3分,共15分)
11.(2024长春中考)若抛物线y=x2-x+c(c是常数)与x轴没有交点,则c的取值范围是 .
12.为了促进城乡协调发展,实现共同富裕,某乡镇计划修建公路.如图,与是公路弯道的外、内边线,它们有共同的圆心O,所对的圆心角都是72°,点A,C,O在同一条直线上,公路弯道外侧边线比内侧边线多36 m,则公路宽AC的长是 m.(π取3.14,计算结果精确到0.1)
13.(2024甘肃中考)如图1为一汽车停车棚,其棚顶的横截面可以看作是抛物线的一部分,如图2是棚顶的竖直高度y(单位:m)与距离停车棚支柱AO的水平距离x(单位:m)近似满足函数关系y=
-0.02x2+0.3x+1.6的图象,点B(6,2.68)在图象上.若一辆厢式货车需在停车棚下避雨,货车截面看作长CD=4 m,高DE=1.8 m的矩形,则可判定货车 完全停到车棚内(填“能”或“不能”).
图1 图2
14.在综合实践课上,数学兴趣小组用所学数学知识测量大汶河某河段的宽度.他们在河岸一侧的瞭望台上放飞一架无人机.如图,无人机在河上方距水面高60 m的点P处测得瞭望台正对岸A处的俯角为50°,测得瞭望台顶端C处的俯角为63.6°,已知瞭望台BC高12 m(图中点A,B,C,P在同一平面内).那么大汶河此河段的宽AB为 m.(参考数据:sin 40°≈,sin 63.6°≈,tan 50°≈,
tan 63.6°≈2)
15.如图,抛物线y=ax2+bx+c的顶点A的坐标为-,n,与x轴的一个交点的横坐标位于0和1之间,则以下结论:①abc>0;②5b+2c<0;③若抛物线经过点(-6,y1),(5,y2),则y1>y2;④若关于x的一元二次方程ax2+bx+c=4无实数根,则n<4.其中正确结论是 (请填写序号).
三、解答题(本题共8小题,共75分.解答应写出文字说明、演算步骤或推理过程)
16.(6分)已知△ABC中,∠A与∠B满足(1-tan A)2+=0.
(1)试判断△ABC的形状;
(2)求(1+sin A)2-2-(3+tan C)0的值.
17.(8分)数学兴趣小组借助无人机开展实物测量的社会实践活动.如图所示,在河岸边的C处,兴趣小组令一架无人机沿67°的仰角方向飞行130 m到达点A处,然后无人机沿水平线AF方向继续飞行30 m至B处,测得此时河对岸D处的俯角为32°.线段AM的长为无人机距地面的铅直高度,点M,C,D在同一条直线上.
(1)求无人机的飞行高度AM;
(2)求CD的长.
18.(8分)某超市购入一批进价为10元/盒的糖果进行销售,经市场调查发现:销售单价不低于进价时,日销售量y(盒)与销售单价x(元)是一次函数关系,下表是y与x的几组对应值.
销售单价x/元 … 12 14 16 18 20 …
销售量y/盒 … 56 52 48 44 40 …
(1)求y与x之间的函数表达式;
(2)糖果销售单价定为多少元时,所获日销售利润最大,最大利润是多少
(3)若超市决定每销售一盒糖果向儿童福利院赠送一件价值为m元的礼品,赠送礼品后,为确保该种糖果日销售获得的最大利润为392元,求m的值.
19.(8分)如图1是我国古代提水的器具桔槔,它选择大小两根竹竿,大竹竿中点架在作为杠杆的竹梯上.大竹竿末端悬挂一个重物,前端连接小竹竿(小竹竿始终与地面垂直),小竹竿上悬挂水桶.其原理是通过对架在竹梯上的大竹竿末端下压用力,从而提水出井.当放松大竹竿时,小竹竿下降,水桶就会回到井里.如图2是桔槔的示意图,大竹竿AB=6 m,O为AB的中点,支架OD垂直地面EF.
图1 图2 图3
(1)当水桶在井里时,∠AOD=120°,求此时支点O到小竹竿AC的距离(结果精确到0.1 m);
(2)如图3,当水桶提到井口时,大竹竿AB旋转至A1B1的位置,小竹竿AC至A1C1的位置,此时
∠A1OD=143°,求点A上升的高度(结果精确到0.1 m).
(参考数据:≈1.73,sin 37°≈0.6,cos 37°≈0.8,tan 37°≈0.75)
20.(10分)(2024包头中考)如图,AB是☉O的直径,BC,BD是☉O的两条弦,点C与点D在AB的两侧,E是OB上一点(OE>BE),连接OC,CE,且∠BOC=2∠BCE.
(1)如图1,若BE=1,CE=,求☉O的半径;
(2)如图2,若BD=2OE,求证:BD∥OC.(请用两种证法解答)
图1 图2
21.(10分)(2024武汉中考)16世纪中叶,我国发明了一种新式火箭“火龙出水”,它是二级火箭的始祖.火箭第一级运行路径形如抛物线,当火箭运行一定水平距离时,自动引发火箭第二级,火箭第二级沿直线运行.某科技小组运用信息技术模拟火箭运行过程.如图,以发射点为原点,地平线为x轴,垂直于地面的直线为y轴,建立平面直角坐标系,分别得到抛物线y=ax2+x和直线y=-x+b.其中,当火箭运行的水平距离为9 km时,自动引发火箭的第二级.
(1)若火箭第二级的引发点的高度为3.6 km,
①直接写出a,b的值;
②火箭在运行过程中,有两个位置的高度比火箭运行的最高点低1.35 km,求这两个位置之间的距离.
(2)直接写出a满足什么条件时,火箭落地点与发射点的水平距离超过15 km.
22.(12分)如图,在四边形ABCD中,AD∥BC,∠DAB=60°,AB=BC=2AD=2.以点A为圆心,以AD为半径作交AB于点E,以点B为圆心,以BE为半径作交BC于点F,连接FD交于另一点G,连接CG.
(1)求证:CG为所在圆的切线;
(2)求图中阴影部分面积.(结果保留π)
23.(13分)(2024达州中考)如图1,抛物线y=ax2+bx-3与x轴交于点A(-3,0)和点B(1,0),与y轴交于点C,点D是抛物线的顶点.
(1)求抛物线的表达式;
(2)如图2,连接AC,DC,直线AC交抛物线的对称轴于点M,若点P是直线AC上方抛物线上一点,且S△PMC=2S△DMC,求点P的坐标;
(3)若点N是抛物线对称轴上位于点D上方的一动点,是否存在以点N,A,C为顶点的三角形是等腰三角形,若存在,请直接写出满足条件的点N的坐标;若不存在,请说明理由.
图1 图2
【详解答案】
1.D 解析:如图,连接DC,由网格可得CD⊥AB,
则DC=,AC=,故sin A=.故选D.
2.C 解析:根据二次函数y=ax2+bx的图象可知,a<0,->0,∴b>0,∴一次函数y=ax+b的图象经过第一、二、四象限,不经过第三象限.故选C.
3.A 解析:过点A作AD⊥BC于点D,如图所示,∵∠BAC=88°,∠C=42°,∴∠B=180°-88°-42°=50°,在Rt△ABD中.AD=AB×sin B=60×sin 50°,∴点A到BC的距离为60sin 50°,故A正确.故选A.
4.A 解析:∵点A到x轴的距离是0.6 dm,∴令y=0.6,则y=-0.1x2+1=0.6.∴x=2或x=-2(舍去).∴点A到y轴的距离为2 dm.又∵点A,B在抛物线上,OA,OB关于y轴对称,∴AB=2×2=4(dm).故选A.
5.B 解析:∵半径OC⊥AB,∴,∴∠AOC=∠BOC=42°,∴∠D=∠AOC=21°,∵OC=OD,∴∠C=∠D=21°,∴∠OED=∠C+∠BOC=21°+42°=63°.故选B.
6.C 解析:∵四边形ABCD是圆内接四边形,∴∠A+∠BCD=180°,∵∠CDF是△ADE的外角,
∴∠CDF=∠A+∠E,∵∠BCD是△CDF的外角,∴∠BCD=∠F+∠CDF,
∴∠BCD=∠F+∠A+∠E,
∴∠A+∠F+∠A+∠E=180°,
∴2∠A+∠F+∠E=180°,∵∠E=54°41',∠F=43°19',∴2∠A+54°41'+43°19'=180°,∴∠A=41°.故选C.
7.D 解析:如图,连接OA,OB,过点O作OM⊥AB,垂足为M,∵六边形ABCDEF是正六边形,点O是它的中心,
∴∠AOB==60°,∵OA=OB,∴△AOB是等边三角形,∵OM⊥AB,∴AM=BM=AB=1,在Rt△AOM中,OA=2,AM=1,∴OM=,即它的内切圆半径为.故选D.
8.A 解析:如图,连接OA,AO',作AB⊥OO'于点B,
∵OA=OO'=AO'=2,∴△AOO'是等边三角形,∴∠AOO'=60°,OB=OO'=1,∴AB=,S弓形AO'=-2×-,∴S阴影=S弓形AO'+S扇形AO'O=--.故选A.
9.B 解析:∵抛物线开口向上,∴a>0,∵对称轴为直线x=-1<0,∴a,b同号,∴b>0,∵抛物线与y轴的交点B在(0,
-2)和(0,-3)之间,∴-3-3,又∵x1x2=,即c=-3a,∵-310.C 解析:由题可知,△CED为直角三角形,而△ABC不是直角三角形,故两三角形不相似,∴CE·CA≠CD·CB,①错误;
如图,连接OD,∵D为BC的中点,O为AB的中点,
∴DO为△ABC的中位线,
∴OD∥AC,
又∵DE⊥AC,∴∠DEA=90°,∴∠ODE=90°,∴DE为☉O的切线,④正确;又∵OB=OD,∴∠ODB=∠B,∵AB为☉O的直径,∴∠ADB=90°,∵∠EDA+∠ADO=90°,∠BDO+∠ADO=90°,∴∠EDA=∠BDO,∴∠EDA=∠B,②正确;
∵D为BC的中点,且AD⊥BC,∴AD垂直平分BC,∴AC=AB,又∵OA=AB,∴OA=AC,③正确;∵∠DAC=∠EAD,∠DEA=∠CDA=90°,∴△ADE∽△ACD,∴,即AD2=AE·AC=AE·AB,⑤正确;则正确结论的个数为4.故选C.
11.c> 解析:∵抛物线y=x2-x+c(c是常数)与x轴没有交点,∴Δ=1-4c<0.∴c>.
12.28.7 解析:由题意-=36,∴OA-OC=≈28.7(m).∴AC=OA-OC=28.7(m).
13.能 解析:∵CD=4 m,B(6,2.68),∴6-4=2,在y=-0.02x2+0.3x+1.6中,当x=2时,y=-0.02×22+0.3×2+1.6=2.12,
∵2.12>1.8,∴货车能完全停到车棚内.
14.74 解析:如图,由题知∠NPC=∠PCF=63.6°,∠MPA=∠BAP=50°,BC=EF=12 m,PE=60 m,∴PF=PE-EF=48 m,
在Rt△PFC,tan 63.6°=≈2,∴CF=24 m,∴BE=24 m,在Rt△APE中,tan 50°=≈,
∴AE=50 m,∴AB=AE+BE=74 m.
15.①②④ 解析:∵抛物线y=ax2+bx+c的顶点A的坐标为-,n,∴-=-.∴a=b,∵抛物线开口向下,∴a<0,
∴b<0,当x=0时,y=c>0,∴abc>0,故①正确.由题中图象可得当x=1时,y=a+b+c<0,∴5b+2c<0,故②正确.∵直线x=-是抛物线的对称轴,∴点(-6,y1)到对称轴的距离大于点(5,y2)到对称轴的距离,∴y116.解:(1)由题意,得
tan A=1,cos B=.
∴∠A=45°,∠B=60°.
∴∠C=180°-∠A-∠B=75°,
∴△ABC是锐角三角形.
(2)原式=-2-1=-1=.
17.解:(1)由题意得AM⊥MD,
在Rt△AMC中,AC=130 m,
∠ACM=67°,
∴AM=AC·sin 67°≈130×=120(m),
∴无人机的飞行高度AM约为120 m.
(2)如图,过点B作BG⊥DM,垂足为G,
由题意得AB=MG=30 m,AM=BG=120 m,∠FBD=32°,AF∥DM,
∴∠FBD=∠BDG=32°,
在Rt△BDG中,DG=≈=192(m),
在Rt△AMC中,AC=130 m,∠ACM=67°,
∴CM=AC·cos 67°≈130×=50(m),
∴CD=MG+DG-CM=30+192-50=172(m),
∴CD的长约为172 m.
18.解:(1)设y=kx+b(k≠0),
∴解得
答:y与x之间的函数表达式为y=-2x+80.
(2)设日销售利润为w元.
w=(x-10)(-2x+80)
=-2x2+100x-800
=-2(x2-50x+625)-800+1 250
=-2(x-25)2+450.
答:糖果销售单价定为25元时,所获日销售利润最大,最大利润是450元.
(3)w=(x-10-m)(-2x+80)=
-2x2+(100+2m)x-800-80m.
∵最大利润为392元,
∴=
392.
整理得m2-60m+116=0.
即(m-2)(m-58)=0.
解得m1=2,m2=58.
当m=58时,x=-=54,
∴每盒糖果的利润=54-10-58=-14(元).
∴舍去.
答:m的值为2.
19.解:(1)如图,过点O作OG⊥AC,垂足为G,
∴∠AGO=90°,
由题意得AC∥OD,
∴∠DOG=∠AGO=90°,
∵∠AOD=120°,
∴∠AOG=∠AOD-∠DOG=30°,
∵O为AB的中点,
∴OA=AB=3(m),
∴在Rt△AOG中,
AG=AO=1.5(m),OG=AG=1.5≈2.6(m),
∴此时支点O到小竹竿AC的距离约为2.6 m.
(2)如图,设OG交A1C1于点H,
由题意得OG⊥A1C1,OD∥A1C1,OA1=OA=3 m,
∴∠A1=180°-∠A1OD=180°-143°=37°,
在Rt△OA1H中,A1H=OA1·cos 37°≈3×0.8=2.4(m),
∵AG=1.5 m,
∴A1H-AG=2.4-1.5=0.9(m),
∴点A上升的高度约为0.9 m.
20.解:(1)如图1,过点O作OH⊥BC于点H.
图1
∵OC=OB,OH⊥BC,
∴∠COH=∠BOH,CH=BH,
∵∠BOC=2∠BCE,
∴∠BOH=∠BCE,
∵∠BOH+∠OBH=90°,
∴∠BCE+∠OBH=90°,
∴∠CEB=90°,
∴BC=,
∴CH=BH=,
∴cos∠OBH=,
∴,
∴OB=3,
∴☉O的半径为3.
(2)证明:证法一 如图2,过点O作OK⊥BD于点K,则BK=DK,
图2
∵BD=2OE,
∴OE=BK,
∵∠CEO=∠OKB=90°,OC=OB,
∴Rt△OEC≌Rt△BKO(HL),
∴∠COE=∠OBK,
∴BD∥OC.
证法二 如图2,过点O作OK⊥BD于点K,则BK=DK,
∵BD=2OE,
∴OE=BK,
∵cos∠COE=,cos∠OBK=,OC=OB,
∴cos∠COE=cos∠OBK,
∴∠COE=∠OBK,
∴BD∥OC.
21.解:(1)①a=-,b=8.1.
②由①得y=-x2+x
=-x2-15x++
=-(0≤x≤9),
∴火箭运行的最高点是 km.
∴-1.35=2.4(km).
∴2.4=-x2+x.
整理得x2-15x+36=0.
解得x1=12>9(不合题意,舍去),x2=3.
由①得y=-x+8.1.
∴2.4=-x+8.1.
解得x=11.4.
∴11.4-3=8.4(km).
答:这两个位置之间的距离为8.4 km.
(2)-解析:当x=9时,y=81a+9.
∴火箭第二级的引发点的坐标为(9,81a+9).
设火箭落地点与发射点的水平距离为15 km,
∴y=-x+b经过点(9,81a+9),(15,0),
∴
解得
∴-22.解:(1)证明:连接BG,如图1,
图1
根据题意可知AD=AE,BE=BF,
又∵AB=BC,
∴CF=AE=AD,
∵BC=2AD,
∴BF=BE=AD=AE=CF,
∵AD∥BC,
∴四边形ABFD是平行四边形,
∴∠BFD=∠DAB=60°,
∵BG=BF,
∴△BFG是等边三角形,
∴GF=BF,∴GF=BF=FC,
∴G在以BC为直径的圆上,
∴∠BGC=90°,
∵BG为所在圆的半径,
∴CG为所在圆的切线.
(2)过点D作DH⊥AB于点H,连接BG,如图2,
图2
由图可得S阴影=S ABFD-S扇形AED-S扇形BEG-S△BFG,
在Rt△AHD中,AD=1,∠DAB=60°,
∴DH=AD·sin∠DAB=1×,
∴S ABFD=AB·DH=2×,
由题可知扇形AED和扇形BEG全等,
∴S扇形AED=S扇形BEG=,
S△BFG=GF·DH=×1×,
∴S阴影=S ABFD-S扇形AED-S扇形BEG-S△BFG=----.
23.解:(1)由题意得y=a(x+3)(x-1)=a(x2+2x-3)=ax2+bx-3,
解得a=1,
则抛物线的表达式为y=x2+2x-3.
(2)由抛物线的表达式知,点C(0,-3)、D(-1,-4),抛物线的对称轴为直线x=-1,
如图,过点D作直线DG∥AC交y轴于点G,在点C上方取点L使CL=2CG,过点L作直线BP∥AC交抛物线于点P,则点P为所求点,
由点A,C坐标得,直线AC的表达式为y=-x-3,
∵DG∥AC,
则直线DG的表达式为y=-(x+1)-4,
则点G(0,-5),则CG=5-3=2,则CL=4,
则点L(0,1),
则直线LP的表达式为y=-x+1,
联立上式和抛物线的表达式得x2+2x-3=-x+1,
解得x=1或x=-4,
即点P的坐标为(1,0)或(-4,5).
(3)存在,点N的坐标为(-1,±)或(-1,-1)或(-1,-3+).
解析:设点N(-1,m),
由点A,C,N的坐标得,AC2=18,AN2=4+m2,CN2=1+(m+3)2,
当AC=AN时,则18=4+m2,
解得m=±,
则点N(-1,±);
当AC=CN或AN=CN时,
则18=1+(m+3)2或4+m2=1+(m+3)2,
解得m=-3+(不合题意的值已舍去)或-1,
则点N(-1,-1)或(-1,-3+),
综上,N(-1,±)或(-1,-1)或(-1,-3+).
(满分:120分 时间:120分钟)
一、选择题(本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.(2024武威凉州区一模)如图所示,△ABC的顶点是正方形网格的格点,则sin A的值为 ( )
A. B. C. D.
2.二次函数y=ax2+bx的图象如图所示,则一次函数y=ax+b的图象不经过 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.如图,一辆自行车竖直摆放在水平地面上,右边是它的部分示意图,现测得∠A=88°,∠C=42°,
AB=60,则点A到BC的距离为 ( )
A.60sin 50° B. C.60cos 50° D.60tan 50°
4.数学来源于生活,伞是生活中常见的一种工具,撑开后如图1所示,由此发现数学知识——抛物线.如图2,以伞柄所在的直线为y轴,以伞骨OA,OB的交点O为坐标原点建立平面直角坐标系.点C为抛物线的顶点,点A,B在抛物线上,OA,OB关于y轴对称.抛物线的表达式为y=-0.1x2+1,若点A到x轴的距离是0.6 dm,则A,B两点之间的距离是 ( )
图1 图2
A.4 dm B.6 dm C.8 dm D.10 dm
5.(2024赤峰中考)如图,AD是☉O的直径,AB是☉O的弦,半径OC⊥AB,连接CD,交OB于点E,
∠BOC=42°,则∠OED的度数是 ( )
A.61° B.63° C.65° D.67°
6.如图,分别延长圆内接四边形ABCD的两组对边,延长线分别相交于点E,F.若∠E=54°41',
∠F=43°19',则∠A的度数为 ( )
A.42° B.41°20' C.41° D.40°20'
7.如图,边长为2的正六边形ABCDEF内接于☉O,则它的内切圆半径为 ( )
A.1 B.2 C. D.
8.(2024泰安中考)两个半径相等的半圆按如图方式放置,半圆O'的一个直径端点与半圆O的圆心重合,若半圆的半径为2,则阴影部分的面积是 ( )
A.π- B.π C.π- D.π-
9.(2024遂宁中考)如图,已知抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)的对称轴为直线x=-1,且该抛物线与x轴交于点A(1,0),与y轴的交点B在(0,-2),(0,-3)之间(不含端点),则下列结论正确的个数是 ( )
①abc>0;②9a-3b+c>0;③
10.如图,线段AB是☉O的直径,☉O交线段BC于点D,且D是BC的中点,DE⊥AC于点E,连接AD,则下列结论正确的个数是 ( )
①CE·CA=CD·CB;②∠EDA=∠B;③OA=AC;④DE是☉O的切线;⑤AD2=AE·AB.
A.2 B.3 C.4 D.5
二、填空题(本题共5小题,每小题3分,共15分)
11.(2024长春中考)若抛物线y=x2-x+c(c是常数)与x轴没有交点,则c的取值范围是 .
12.为了促进城乡协调发展,实现共同富裕,某乡镇计划修建公路.如图,与是公路弯道的外、内边线,它们有共同的圆心O,所对的圆心角都是72°,点A,C,O在同一条直线上,公路弯道外侧边线比内侧边线多36 m,则公路宽AC的长是 m.(π取3.14,计算结果精确到0.1)
13.(2024甘肃中考)如图1为一汽车停车棚,其棚顶的横截面可以看作是抛物线的一部分,如图2是棚顶的竖直高度y(单位:m)与距离停车棚支柱AO的水平距离x(单位:m)近似满足函数关系y=
-0.02x2+0.3x+1.6的图象,点B(6,2.68)在图象上.若一辆厢式货车需在停车棚下避雨,货车截面看作长CD=4 m,高DE=1.8 m的矩形,则可判定货车 完全停到车棚内(填“能”或“不能”).
图1 图2
14.在综合实践课上,数学兴趣小组用所学数学知识测量大汶河某河段的宽度.他们在河岸一侧的瞭望台上放飞一架无人机.如图,无人机在河上方距水面高60 m的点P处测得瞭望台正对岸A处的俯角为50°,测得瞭望台顶端C处的俯角为63.6°,已知瞭望台BC高12 m(图中点A,B,C,P在同一平面内).那么大汶河此河段的宽AB为 m.(参考数据:sin 40°≈,sin 63.6°≈,tan 50°≈,
tan 63.6°≈2)
15.如图,抛物线y=ax2+bx+c的顶点A的坐标为-,n,与x轴的一个交点的横坐标位于0和1之间,则以下结论:①abc>0;②5b+2c<0;③若抛物线经过点(-6,y1),(5,y2),则y1>y2;④若关于x的一元二次方程ax2+bx+c=4无实数根,则n<4.其中正确结论是 (请填写序号).
三、解答题(本题共8小题,共75分.解答应写出文字说明、演算步骤或推理过程)
16.(6分)已知△ABC中,∠A与∠B满足(1-tan A)2+=0.
(1)试判断△ABC的形状;
(2)求(1+sin A)2-2-(3+tan C)0的值.
17.(8分)数学兴趣小组借助无人机开展实物测量的社会实践活动.如图所示,在河岸边的C处,兴趣小组令一架无人机沿67°的仰角方向飞行130 m到达点A处,然后无人机沿水平线AF方向继续飞行30 m至B处,测得此时河对岸D处的俯角为32°.线段AM的长为无人机距地面的铅直高度,点M,C,D在同一条直线上.
(1)求无人机的飞行高度AM;
(2)求CD的长.
18.(8分)某超市购入一批进价为10元/盒的糖果进行销售,经市场调查发现:销售单价不低于进价时,日销售量y(盒)与销售单价x(元)是一次函数关系,下表是y与x的几组对应值.
销售单价x/元 … 12 14 16 18 20 …
销售量y/盒 … 56 52 48 44 40 …
(1)求y与x之间的函数表达式;
(2)糖果销售单价定为多少元时,所获日销售利润最大,最大利润是多少
(3)若超市决定每销售一盒糖果向儿童福利院赠送一件价值为m元的礼品,赠送礼品后,为确保该种糖果日销售获得的最大利润为392元,求m的值.
19.(8分)如图1是我国古代提水的器具桔槔,它选择大小两根竹竿,大竹竿中点架在作为杠杆的竹梯上.大竹竿末端悬挂一个重物,前端连接小竹竿(小竹竿始终与地面垂直),小竹竿上悬挂水桶.其原理是通过对架在竹梯上的大竹竿末端下压用力,从而提水出井.当放松大竹竿时,小竹竿下降,水桶就会回到井里.如图2是桔槔的示意图,大竹竿AB=6 m,O为AB的中点,支架OD垂直地面EF.
图1 图2 图3
(1)当水桶在井里时,∠AOD=120°,求此时支点O到小竹竿AC的距离(结果精确到0.1 m);
(2)如图3,当水桶提到井口时,大竹竿AB旋转至A1B1的位置,小竹竿AC至A1C1的位置,此时
∠A1OD=143°,求点A上升的高度(结果精确到0.1 m).
(参考数据:≈1.73,sin 37°≈0.6,cos 37°≈0.8,tan 37°≈0.75)
20.(10分)(2024包头中考)如图,AB是☉O的直径,BC,BD是☉O的两条弦,点C与点D在AB的两侧,E是OB上一点(OE>BE),连接OC,CE,且∠BOC=2∠BCE.
(1)如图1,若BE=1,CE=,求☉O的半径;
(2)如图2,若BD=2OE,求证:BD∥OC.(请用两种证法解答)
图1 图2
21.(10分)(2024武汉中考)16世纪中叶,我国发明了一种新式火箭“火龙出水”,它是二级火箭的始祖.火箭第一级运行路径形如抛物线,当火箭运行一定水平距离时,自动引发火箭第二级,火箭第二级沿直线运行.某科技小组运用信息技术模拟火箭运行过程.如图,以发射点为原点,地平线为x轴,垂直于地面的直线为y轴,建立平面直角坐标系,分别得到抛物线y=ax2+x和直线y=-x+b.其中,当火箭运行的水平距离为9 km时,自动引发火箭的第二级.
(1)若火箭第二级的引发点的高度为3.6 km,
①直接写出a,b的值;
②火箭在运行过程中,有两个位置的高度比火箭运行的最高点低1.35 km,求这两个位置之间的距离.
(2)直接写出a满足什么条件时,火箭落地点与发射点的水平距离超过15 km.
22.(12分)如图,在四边形ABCD中,AD∥BC,∠DAB=60°,AB=BC=2AD=2.以点A为圆心,以AD为半径作交AB于点E,以点B为圆心,以BE为半径作交BC于点F,连接FD交于另一点G,连接CG.
(1)求证:CG为所在圆的切线;
(2)求图中阴影部分面积.(结果保留π)
23.(13分)(2024达州中考)如图1,抛物线y=ax2+bx-3与x轴交于点A(-3,0)和点B(1,0),与y轴交于点C,点D是抛物线的顶点.
(1)求抛物线的表达式;
(2)如图2,连接AC,DC,直线AC交抛物线的对称轴于点M,若点P是直线AC上方抛物线上一点,且S△PMC=2S△DMC,求点P的坐标;
(3)若点N是抛物线对称轴上位于点D上方的一动点,是否存在以点N,A,C为顶点的三角形是等腰三角形,若存在,请直接写出满足条件的点N的坐标;若不存在,请说明理由.
图1 图2
【详解答案】
1.D 解析:如图,连接DC,由网格可得CD⊥AB,
则DC=,AC=,故sin A=.故选D.
2.C 解析:根据二次函数y=ax2+bx的图象可知,a<0,->0,∴b>0,∴一次函数y=ax+b的图象经过第一、二、四象限,不经过第三象限.故选C.
3.A 解析:过点A作AD⊥BC于点D,如图所示,∵∠BAC=88°,∠C=42°,∴∠B=180°-88°-42°=50°,在Rt△ABD中.AD=AB×sin B=60×sin 50°,∴点A到BC的距离为60sin 50°,故A正确.故选A.
4.A 解析:∵点A到x轴的距离是0.6 dm,∴令y=0.6,则y=-0.1x2+1=0.6.∴x=2或x=-2(舍去).∴点A到y轴的距离为2 dm.又∵点A,B在抛物线上,OA,OB关于y轴对称,∴AB=2×2=4(dm).故选A.
5.B 解析:∵半径OC⊥AB,∴,∴∠AOC=∠BOC=42°,∴∠D=∠AOC=21°,∵OC=OD,∴∠C=∠D=21°,∴∠OED=∠C+∠BOC=21°+42°=63°.故选B.
6.C 解析:∵四边形ABCD是圆内接四边形,∴∠A+∠BCD=180°,∵∠CDF是△ADE的外角,
∴∠CDF=∠A+∠E,∵∠BCD是△CDF的外角,∴∠BCD=∠F+∠CDF,
∴∠BCD=∠F+∠A+∠E,
∴∠A+∠F+∠A+∠E=180°,
∴2∠A+∠F+∠E=180°,∵∠E=54°41',∠F=43°19',∴2∠A+54°41'+43°19'=180°,∴∠A=41°.故选C.
7.D 解析:如图,连接OA,OB,过点O作OM⊥AB,垂足为M,∵六边形ABCDEF是正六边形,点O是它的中心,
∴∠AOB==60°,∵OA=OB,∴△AOB是等边三角形,∵OM⊥AB,∴AM=BM=AB=1,在Rt△AOM中,OA=2,AM=1,∴OM=,即它的内切圆半径为.故选D.
8.A 解析:如图,连接OA,AO',作AB⊥OO'于点B,
∵OA=OO'=AO'=2,∴△AOO'是等边三角形,∴∠AOO'=60°,OB=OO'=1,∴AB=,S弓形AO'=-2×-,∴S阴影=S弓形AO'+S扇形AO'O=--.故选A.
9.B 解析:∵抛物线开口向上,∴a>0,∵对称轴为直线x=-1<0,∴a,b同号,∴b>0,∵抛物线与y轴的交点B在(0,
-2)和(0,-3)之间,∴-3
如图,连接OD,∵D为BC的中点,O为AB的中点,
∴DO为△ABC的中位线,
∴OD∥AC,
又∵DE⊥AC,∴∠DEA=90°,∴∠ODE=90°,∴DE为☉O的切线,④正确;又∵OB=OD,∴∠ODB=∠B,∵AB为☉O的直径,∴∠ADB=90°,∵∠EDA+∠ADO=90°,∠BDO+∠ADO=90°,∴∠EDA=∠BDO,∴∠EDA=∠B,②正确;
∵D为BC的中点,且AD⊥BC,∴AD垂直平分BC,∴AC=AB,又∵OA=AB,∴OA=AC,③正确;∵∠DAC=∠EAD,∠DEA=∠CDA=90°,∴△ADE∽△ACD,∴,即AD2=AE·AC=AE·AB,⑤正确;则正确结论的个数为4.故选C.
11.c> 解析:∵抛物线y=x2-x+c(c是常数)与x轴没有交点,∴Δ=1-4c<0.∴c>.
12.28.7 解析:由题意-=36,∴OA-OC=≈28.7(m).∴AC=OA-OC=28.7(m).
13.能 解析:∵CD=4 m,B(6,2.68),∴6-4=2,在y=-0.02x2+0.3x+1.6中,当x=2时,y=-0.02×22+0.3×2+1.6=2.12,
∵2.12>1.8,∴货车能完全停到车棚内.
14.74 解析:如图,由题知∠NPC=∠PCF=63.6°,∠MPA=∠BAP=50°,BC=EF=12 m,PE=60 m,∴PF=PE-EF=48 m,
在Rt△PFC,tan 63.6°=≈2,∴CF=24 m,∴BE=24 m,在Rt△APE中,tan 50°=≈,
∴AE=50 m,∴AB=AE+BE=74 m.
15.①②④ 解析:∵抛物线y=ax2+bx+c的顶点A的坐标为-,n,∴-=-.∴a=b,∵抛物线开口向下,∴a<0,
∴b<0,当x=0时,y=c>0,∴abc>0,故①正确.由题中图象可得当x=1时,y=a+b+c<0,∴5b+2c<0,故②正确.∵直线x=-是抛物线的对称轴,∴点(-6,y1)到对称轴的距离大于点(5,y2)到对称轴的距离,∴y1
tan A=1,cos B=.
∴∠A=45°,∠B=60°.
∴∠C=180°-∠A-∠B=75°,
∴△ABC是锐角三角形.
(2)原式=-2-1=-1=.
17.解:(1)由题意得AM⊥MD,
在Rt△AMC中,AC=130 m,
∠ACM=67°,
∴AM=AC·sin 67°≈130×=120(m),
∴无人机的飞行高度AM约为120 m.
(2)如图,过点B作BG⊥DM,垂足为G,
由题意得AB=MG=30 m,AM=BG=120 m,∠FBD=32°,AF∥DM,
∴∠FBD=∠BDG=32°,
在Rt△BDG中,DG=≈=192(m),
在Rt△AMC中,AC=130 m,∠ACM=67°,
∴CM=AC·cos 67°≈130×=50(m),
∴CD=MG+DG-CM=30+192-50=172(m),
∴CD的长约为172 m.
18.解:(1)设y=kx+b(k≠0),
∴解得
答:y与x之间的函数表达式为y=-2x+80.
(2)设日销售利润为w元.
w=(x-10)(-2x+80)
=-2x2+100x-800
=-2(x2-50x+625)-800+1 250
=-2(x-25)2+450.
答:糖果销售单价定为25元时,所获日销售利润最大,最大利润是450元.
(3)w=(x-10-m)(-2x+80)=
-2x2+(100+2m)x-800-80m.
∵最大利润为392元,
∴=
392.
整理得m2-60m+116=0.
即(m-2)(m-58)=0.
解得m1=2,m2=58.
当m=58时,x=-=54,
∴每盒糖果的利润=54-10-58=-14(元).
∴舍去.
答:m的值为2.
19.解:(1)如图,过点O作OG⊥AC,垂足为G,
∴∠AGO=90°,
由题意得AC∥OD,
∴∠DOG=∠AGO=90°,
∵∠AOD=120°,
∴∠AOG=∠AOD-∠DOG=30°,
∵O为AB的中点,
∴OA=AB=3(m),
∴在Rt△AOG中,
AG=AO=1.5(m),OG=AG=1.5≈2.6(m),
∴此时支点O到小竹竿AC的距离约为2.6 m.
(2)如图,设OG交A1C1于点H,
由题意得OG⊥A1C1,OD∥A1C1,OA1=OA=3 m,
∴∠A1=180°-∠A1OD=180°-143°=37°,
在Rt△OA1H中,A1H=OA1·cos 37°≈3×0.8=2.4(m),
∵AG=1.5 m,
∴A1H-AG=2.4-1.5=0.9(m),
∴点A上升的高度约为0.9 m.
20.解:(1)如图1,过点O作OH⊥BC于点H.
图1
∵OC=OB,OH⊥BC,
∴∠COH=∠BOH,CH=BH,
∵∠BOC=2∠BCE,
∴∠BOH=∠BCE,
∵∠BOH+∠OBH=90°,
∴∠BCE+∠OBH=90°,
∴∠CEB=90°,
∴BC=,
∴CH=BH=,
∴cos∠OBH=,
∴,
∴OB=3,
∴☉O的半径为3.
(2)证明:证法一 如图2,过点O作OK⊥BD于点K,则BK=DK,
图2
∵BD=2OE,
∴OE=BK,
∵∠CEO=∠OKB=90°,OC=OB,
∴Rt△OEC≌Rt△BKO(HL),
∴∠COE=∠OBK,
∴BD∥OC.
证法二 如图2,过点O作OK⊥BD于点K,则BK=DK,
∵BD=2OE,
∴OE=BK,
∵cos∠COE=,cos∠OBK=,OC=OB,
∴cos∠COE=cos∠OBK,
∴∠COE=∠OBK,
∴BD∥OC.
21.解:(1)①a=-,b=8.1.
②由①得y=-x2+x
=-x2-15x++
=-(0≤x≤9),
∴火箭运行的最高点是 km.
∴-1.35=2.4(km).
∴2.4=-x2+x.
整理得x2-15x+36=0.
解得x1=12>9(不合题意,舍去),x2=3.
由①得y=-x+8.1.
∴2.4=-x+8.1.
解得x=11.4.
∴11.4-3=8.4(km).
答:这两个位置之间的距离为8.4 km.
(2)-
∴火箭第二级的引发点的坐标为(9,81a+9).
设火箭落地点与发射点的水平距离为15 km,
∴y=-x+b经过点(9,81a+9),(15,0),
∴
解得
∴-
图1
根据题意可知AD=AE,BE=BF,
又∵AB=BC,
∴CF=AE=AD,
∵BC=2AD,
∴BF=BE=AD=AE=CF,
∵AD∥BC,
∴四边形ABFD是平行四边形,
∴∠BFD=∠DAB=60°,
∵BG=BF,
∴△BFG是等边三角形,
∴GF=BF,∴GF=BF=FC,
∴G在以BC为直径的圆上,
∴∠BGC=90°,
∵BG为所在圆的半径,
∴CG为所在圆的切线.
(2)过点D作DH⊥AB于点H,连接BG,如图2,
图2
由图可得S阴影=S ABFD-S扇形AED-S扇形BEG-S△BFG,
在Rt△AHD中,AD=1,∠DAB=60°,
∴DH=AD·sin∠DAB=1×,
∴S ABFD=AB·DH=2×,
由题可知扇形AED和扇形BEG全等,
∴S扇形AED=S扇形BEG=,
S△BFG=GF·DH=×1×,
∴S阴影=S ABFD-S扇形AED-S扇形BEG-S△BFG=----.
23.解:(1)由题意得y=a(x+3)(x-1)=a(x2+2x-3)=ax2+bx-3,
解得a=1,
则抛物线的表达式为y=x2+2x-3.
(2)由抛物线的表达式知,点C(0,-3)、D(-1,-4),抛物线的对称轴为直线x=-1,
如图,过点D作直线DG∥AC交y轴于点G,在点C上方取点L使CL=2CG,过点L作直线BP∥AC交抛物线于点P,则点P为所求点,
由点A,C坐标得,直线AC的表达式为y=-x-3,
∵DG∥AC,
则直线DG的表达式为y=-(x+1)-4,
则点G(0,-5),则CG=5-3=2,则CL=4,
则点L(0,1),
则直线LP的表达式为y=-x+1,
联立上式和抛物线的表达式得x2+2x-3=-x+1,
解得x=1或x=-4,
即点P的坐标为(1,0)或(-4,5).
(3)存在,点N的坐标为(-1,±)或(-1,-1)或(-1,-3+).
解析:设点N(-1,m),
由点A,C,N的坐标得,AC2=18,AN2=4+m2,CN2=1+(m+3)2,
当AC=AN时,则18=4+m2,
解得m=±,
则点N(-1,±);
当AC=CN或AN=CN时,
则18=1+(m+3)2或4+m2=1+(m+3)2,
解得m=-3+(不合题意的值已舍去)或-1,
则点N(-1,-1)或(-1,-3+),
综上,N(-1,±)或(-1,-1)或(-1,-3+).
同课章节目录
