26.2.3.求二次函数的表达式 课时作业(含答案) 2024-2025学年数学华东师大版九年级下册
文档属性
| 名称 | 26.2.3.求二次函数的表达式 课时作业(含答案) 2024-2025学年数学华东师大版九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 107.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-26 21:34:03 | ||
图片预览


文档简介
3.求二次函数的表达式
求二次函数的表达式
1.(2024合肥月考)抛物线y=x2+bx+c与y轴的交点坐标为(0,-3),则抛物线的表达式为 ( )
A.y=x2+bx+3 B.y=x2+bx-3 C.y=x2+3x+c D.y=x2-3x+c
2.抛物线y=2x2+c的顶点坐标为(0,1),则抛物线的表达式为 ( )
A.y=2x2+1 B.y=2x2-1 C.y=2x2+2 D.y=2x2-2
3.(2024长沙期末)一个二次函数图象的顶点坐标是(2,4),且过另一点(0,-4),则这个二次函数的表达式为 ( )
A.y=-2(x+2)2+4 B.y=2(x+2)2-4 C.y=-2(x-2)2+4 D.y=2(x-2)2-4
4.某同学在用描点法画二次函数y=ax2+bx+c的图象时,列出了下面的表格:
x … -2 -1 0 1 2 …
y … -11 -2 1 -2 -5 …
由于粗心,他算错了一个y值,则这个错误的数值是 .
5.甲、乙、丙三名同学每人抽取一张卡片,每张卡片上有一个形如y=ax2+bx的二次函数的表达式,其中只有一人与其他两人抽到的表达式不同.下面是他们对抽到的表达式所对应的图象的描述:
甲:开口向下;
乙:顶点在第三象限;
丙:经过点(-2,0),(1,3).
根据描述可知,抽到与其他两人表达式不同的是 .(填“甲”“乙”或“丙”)
6.已知一个二次函数的图象过点(-1,10),(1,4),(0,3),求这个二次函数的表达式.
7.已知抛物线y=ax2经过点A(2,-8),求:
(1)该抛物线的表达式;
(2)判断点B(3,-18)是否在该抛物线上;
(3)求出此抛物线上纵坐标是-50的点的坐标.
1.已知二次函数的图象如图所示,则其表达式可能为 ( )
A.y=-3x2-1 B.y=-3x2+1 C.y=3x2+1 D.y=3x2-1
2.已知抛物线y=ax2+bx经过点A(-3,-3),且该抛物线的对称轴经过点A,则该抛物线的表达式为 ( )
A.y=-x2-2x B.y=-x2+2x C.y=x2-2x D.y=x2+2x
3.(开放型试题)一个二次函数y=ax2+bx+c的图象的顶点在y轴正半轴上,且其对称轴左侧的部分是上升的,那么这个二次函数的表达式可以是 .
4.(易错题)设抛物线y=ax2+bx+c(a≠0)过A(0,2),B(4,3),C三点,其中点C在直线x=2上,且点C到抛物线的对称轴的距离等于1,则抛物线的函数表达式为 .
5.规定:两个函数y1、y2的图象关于y轴对称,则称这两个函数互为“Y函数”.例如:函数y1=2x+2与y2=-2x+2的图象关于y轴对称,则这两个函数互为“Y函数”.若函数y=kx2+2(k-1)x+k-3(k为常数)的“Y函数”图象与x轴只有一个交点,则其“Y函数”的表达式为 .
6.如图,二次函数y=x2+bx+c的图象过点B(0,-2).它与反比例函数y=-(x<0)的图象交于点A(m,4),求这个二次函数的表达式.
7.已知抛物线y=ax2-2ax-3+2a2(a≠0).
(1)求这条抛物线的对称轴;
(2)若该抛物线的顶点在x轴上,求其表达式;
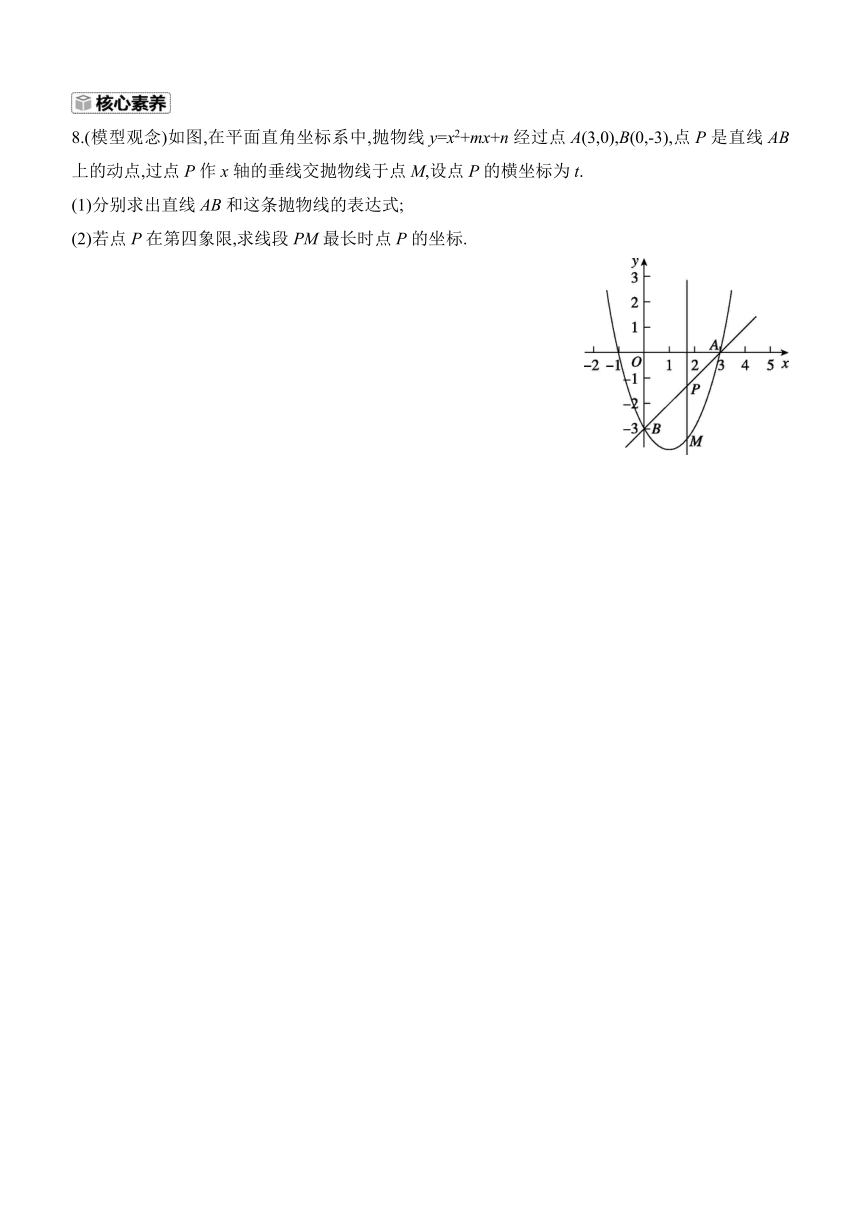
(3)设点P(m,y1),Q(3,y2)在抛物线上,若y18.(模型观念)如图,在平面直角坐标系中,抛物线y=x2+mx+n经过点A(3,0),B(0,-3),点P是直线AB上的动点,过点P作x轴的垂线交抛物线于点M,设点P的横坐标为t.
(1)分别求出直线AB和这条抛物线的表达式;
(2)若点P在第四象限,求线段PM最长时点P的坐标.
【详解答案】
课堂达标
1.B 2.A 3.C 4.-5 5.甲
6.解:设所求二次函数的表达式为y=ax2+bx+c(a≠0),根据题意,得解得
∴所求二次函数的表达式为y=4x2-3x+3.
7.解:(1)把点A(2,-8)的坐标代入y=ax2,得-8=a×22,解得a=-2,
∴抛物线的表达式为y=-2x2.
(2)∵-2×32=-18,
∴点B(3,-18)在该抛物线上.
(3)由题意,得-2x2=-50,解得x=±5,
∴此抛物线上纵坐标是-50的点的坐标为(5,-50),(-5,-50).
课后提升
1.B 解析:由题意,抛物线的开口向下,顶点是(0,1),对称轴是y轴,
∴B选项正确,A、C、D错误.故选B.
2.D 解析:∵抛物线y=ax2+bx经过点A(-3,-3),且抛物线的对称轴经过点A,
∴抛物线的顶点坐标是(-3,-3).
∴解得
∴该抛物线的表达式为y=x2+2x.
故选D.
3.y=-x2+1(答案不唯一)
解析:由题意,得b=0,a<0,c>0,
∴这个二次函数的表达式可以是y=-x2+1.(答案不唯一)
4.y=x2-x+2或y=-x2+x+2 解析:∵抛物线y=ax2+bx+c(a≠0)过点A(0,2),
∴函数表达式为y=ax2+bx+2.
∵点C在直线x=2上且到抛物线的对称轴的距离等于1,可得对称轴为直线x=1或直线x=3,
∴可以建立以下两个方程组:
(1)
(2)
由方程组(1)解得
由方程组(2)解得
∴抛物线的函数表达式为y=x2-x+2或y=-x2+x+2.
5.y=2x-3或y=-x2+4x-4
解析:∵函数y=kx2+2(k-1)x+k-3(k为常数)的“Y函数”图象与x轴只有一个交点,∴函数y=kx2+2(k-1)x+k-3(k为常数)的图象与x轴也只有一个交点.
当k=0时,函数表达式为y=-2x-3,它的“Y函数”的表达式为y=2x-3,它们的图象与x轴只有一个交点;
当k≠0时,此函数是二次函数,
∵它们的图象与x轴都只有一个交点,
∴它们的顶点都在x轴上.
∴=0.
解得k=-1,
∴原函数的表达式为y=-x2-4x-4=-(x+2)2.
∴它的“Y函数”的表达式为y=-(x-2)2=-x2+4x-4.
综上,其“Y函数”的表达式为y=2x-3或y=-x2+4x-4.
6.解:把点A(m,4)的坐标代入y=-,得-=4,解得m=-3,则A(-3,4),把A(-3,4),B(0,-2)的坐标代入y=x2+bx+c,得
解得
∴这个二次函数的表达式为y=x2+x-2.
7.解:(1)∵抛物线y=ax2-2ax-3+2a2=a(x-1)2+2a2-a-3,
∴抛物线的对称轴为直线x=1.
(2)∵抛物线的顶点在x轴上,
∴2a2-a-3=0.
解得a=或a=-1,
∴抛物线的表达式为y=x2-3x+或y=-x2+2x-1.
(3)抛物线的对称轴为直线x=1,
Q(3,y2)关于直线x=1的对称点的坐标为(-1,y2),
分情况讨论:
①当a>0时,要使y1②当a<0时,要使y13.
8.解:(1)由抛物线y=x2+mx+n经过点A(3,0),B(0,-3),得
解得
∴y=x2-2x-3.
设直线AB的表达式为y=kx+b(k≠0),由直线AB经过点A(3,0),B(0,-3),得
解得
∴直线AB的表达式为y=x-3.
(2)由题意得P(t,t-3)(0∴PM=t-3-(t2-2t-3)=-t2+3t=-.
当t=时,PM取得最大值,此时t-3=-.
∴P.
求二次函数的表达式
1.(2024合肥月考)抛物线y=x2+bx+c与y轴的交点坐标为(0,-3),则抛物线的表达式为 ( )
A.y=x2+bx+3 B.y=x2+bx-3 C.y=x2+3x+c D.y=x2-3x+c
2.抛物线y=2x2+c的顶点坐标为(0,1),则抛物线的表达式为 ( )
A.y=2x2+1 B.y=2x2-1 C.y=2x2+2 D.y=2x2-2
3.(2024长沙期末)一个二次函数图象的顶点坐标是(2,4),且过另一点(0,-4),则这个二次函数的表达式为 ( )
A.y=-2(x+2)2+4 B.y=2(x+2)2-4 C.y=-2(x-2)2+4 D.y=2(x-2)2-4
4.某同学在用描点法画二次函数y=ax2+bx+c的图象时,列出了下面的表格:
x … -2 -1 0 1 2 …
y … -11 -2 1 -2 -5 …
由于粗心,他算错了一个y值,则这个错误的数值是 .
5.甲、乙、丙三名同学每人抽取一张卡片,每张卡片上有一个形如y=ax2+bx的二次函数的表达式,其中只有一人与其他两人抽到的表达式不同.下面是他们对抽到的表达式所对应的图象的描述:
甲:开口向下;
乙:顶点在第三象限;
丙:经过点(-2,0),(1,3).
根据描述可知,抽到与其他两人表达式不同的是 .(填“甲”“乙”或“丙”)
6.已知一个二次函数的图象过点(-1,10),(1,4),(0,3),求这个二次函数的表达式.
7.已知抛物线y=ax2经过点A(2,-8),求:
(1)该抛物线的表达式;
(2)判断点B(3,-18)是否在该抛物线上;
(3)求出此抛物线上纵坐标是-50的点的坐标.
1.已知二次函数的图象如图所示,则其表达式可能为 ( )
A.y=-3x2-1 B.y=-3x2+1 C.y=3x2+1 D.y=3x2-1
2.已知抛物线y=ax2+bx经过点A(-3,-3),且该抛物线的对称轴经过点A,则该抛物线的表达式为 ( )
A.y=-x2-2x B.y=-x2+2x C.y=x2-2x D.y=x2+2x
3.(开放型试题)一个二次函数y=ax2+bx+c的图象的顶点在y轴正半轴上,且其对称轴左侧的部分是上升的,那么这个二次函数的表达式可以是 .
4.(易错题)设抛物线y=ax2+bx+c(a≠0)过A(0,2),B(4,3),C三点,其中点C在直线x=2上,且点C到抛物线的对称轴的距离等于1,则抛物线的函数表达式为 .
5.规定:两个函数y1、y2的图象关于y轴对称,则称这两个函数互为“Y函数”.例如:函数y1=2x+2与y2=-2x+2的图象关于y轴对称,则这两个函数互为“Y函数”.若函数y=kx2+2(k-1)x+k-3(k为常数)的“Y函数”图象与x轴只有一个交点,则其“Y函数”的表达式为 .
6.如图,二次函数y=x2+bx+c的图象过点B(0,-2).它与反比例函数y=-(x<0)的图象交于点A(m,4),求这个二次函数的表达式.
7.已知抛物线y=ax2-2ax-3+2a2(a≠0).
(1)求这条抛物线的对称轴;
(2)若该抛物线的顶点在x轴上,求其表达式;
(3)设点P(m,y1),Q(3,y2)在抛物线上,若y1
(1)分别求出直线AB和这条抛物线的表达式;
(2)若点P在第四象限,求线段PM最长时点P的坐标.
【详解答案】
课堂达标
1.B 2.A 3.C 4.-5 5.甲
6.解:设所求二次函数的表达式为y=ax2+bx+c(a≠0),根据题意,得解得
∴所求二次函数的表达式为y=4x2-3x+3.
7.解:(1)把点A(2,-8)的坐标代入y=ax2,得-8=a×22,解得a=-2,
∴抛物线的表达式为y=-2x2.
(2)∵-2×32=-18,
∴点B(3,-18)在该抛物线上.
(3)由题意,得-2x2=-50,解得x=±5,
∴此抛物线上纵坐标是-50的点的坐标为(5,-50),(-5,-50).
课后提升
1.B 解析:由题意,抛物线的开口向下,顶点是(0,1),对称轴是y轴,
∴B选项正确,A、C、D错误.故选B.
2.D 解析:∵抛物线y=ax2+bx经过点A(-3,-3),且抛物线的对称轴经过点A,
∴抛物线的顶点坐标是(-3,-3).
∴解得
∴该抛物线的表达式为y=x2+2x.
故选D.
3.y=-x2+1(答案不唯一)
解析:由题意,得b=0,a<0,c>0,
∴这个二次函数的表达式可以是y=-x2+1.(答案不唯一)
4.y=x2-x+2或y=-x2+x+2 解析:∵抛物线y=ax2+bx+c(a≠0)过点A(0,2),
∴函数表达式为y=ax2+bx+2.
∵点C在直线x=2上且到抛物线的对称轴的距离等于1,可得对称轴为直线x=1或直线x=3,
∴可以建立以下两个方程组:
(1)
(2)
由方程组(1)解得
由方程组(2)解得
∴抛物线的函数表达式为y=x2-x+2或y=-x2+x+2.
5.y=2x-3或y=-x2+4x-4
解析:∵函数y=kx2+2(k-1)x+k-3(k为常数)的“Y函数”图象与x轴只有一个交点,∴函数y=kx2+2(k-1)x+k-3(k为常数)的图象与x轴也只有一个交点.
当k=0时,函数表达式为y=-2x-3,它的“Y函数”的表达式为y=2x-3,它们的图象与x轴只有一个交点;
当k≠0时,此函数是二次函数,
∵它们的图象与x轴都只有一个交点,
∴它们的顶点都在x轴上.
∴=0.
解得k=-1,
∴原函数的表达式为y=-x2-4x-4=-(x+2)2.
∴它的“Y函数”的表达式为y=-(x-2)2=-x2+4x-4.
综上,其“Y函数”的表达式为y=2x-3或y=-x2+4x-4.
6.解:把点A(m,4)的坐标代入y=-,得-=4,解得m=-3,则A(-3,4),把A(-3,4),B(0,-2)的坐标代入y=x2+bx+c,得
解得
∴这个二次函数的表达式为y=x2+x-2.
7.解:(1)∵抛物线y=ax2-2ax-3+2a2=a(x-1)2+2a2-a-3,
∴抛物线的对称轴为直线x=1.
(2)∵抛物线的顶点在x轴上,
∴2a2-a-3=0.
解得a=或a=-1,
∴抛物线的表达式为y=x2-3x+或y=-x2+2x-1.
(3)抛物线的对称轴为直线x=1,
Q(3,y2)关于直线x=1的对称点的坐标为(-1,y2),
分情况讨论:
①当a>0时,要使y1
8.解:(1)由抛物线y=x2+mx+n经过点A(3,0),B(0,-3),得
解得
∴y=x2-2x-3.
设直线AB的表达式为y=kx+b(k≠0),由直线AB经过点A(3,0),B(0,-3),得
解得
∴直线AB的表达式为y=x-3.
(2)由题意得P(t,t-3)(0
当t=时,PM取得最大值,此时t-3=-.
∴P.
