27.1圆的认识 课时作业 (含答案)2024-2025学年数学华东师大版九年级下册
文档属性
| 名称 | 27.1圆的认识 课时作业 (含答案)2024-2025学年数学华东师大版九年级下册 | 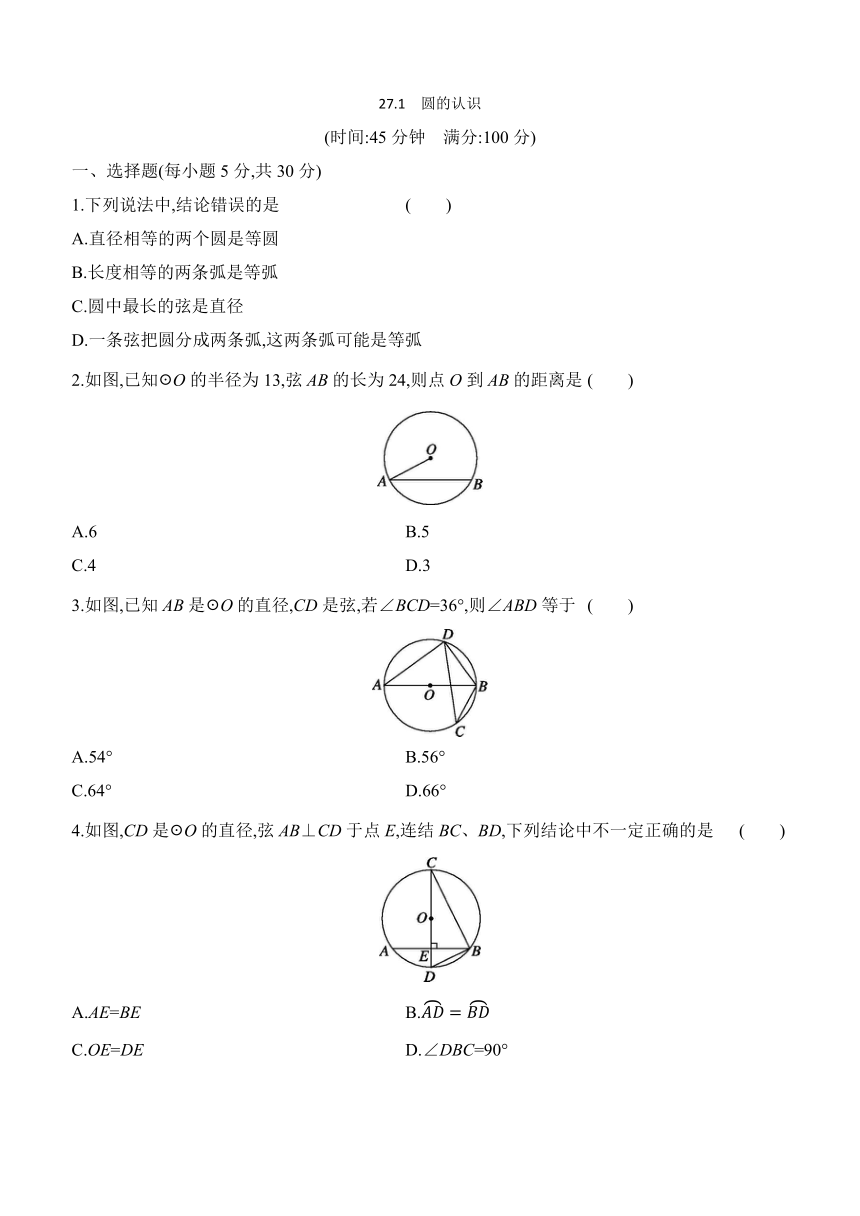 | |
| 格式 | docx | ||
| 文件大小 | 205.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-26 21:35:17 | ||
图片预览




文档简介
27.1 圆的认识
(时间:45分钟 满分:100分)
一、选择题(每小题5分,共30分)
1.下列说法中,结论错误的是 ( )
A.直径相等的两个圆是等圆
B.长度相等的两条弧是等弧
C.圆中最长的弦是直径
D.一条弦把圆分成两条弧,这两条弧可能是等弧
2.如图,已知☉O的半径为13,弦AB的长为24,则点O到AB的距离是 ( )
A.6 B.5
C.4 D.3
3.如图,已知AB是☉O的直径,CD是弦,若∠BCD=36°,则∠ABD等于 ( )
A.54° B.56°
C.64° D.66°
4.如图,CD是☉O的直径,弦AB⊥CD于点E,连结BC、BD,下列结论中不一定正确的是 ( )
A.AE=BE B.
C.OE=DE D.∠DBC=90°
5.如图,在平面直角坐标系中,☉O经过点(0,10),直线y=kx+2k-4与☉O交于B、C两点,则弦BC的最小值是 ( )
A.6 B.10 C.8 D.以上都不对
6.如图,在☉O中,AB是直径,BC是弦,点P是上任意一点.若AB=5,BC=3,则AP的长不可能为 ( )
A.3 B.4 C. D.5
二、填空题(每小题5分,共25分)
7.如图,延长☉O的弦AB、半径OC交于点D,BD=OA.若∠AOC=120°,则∠D的度数是 .
8.如图,AB是☉O的直径,点C、D、E都在☉O上,∠1=55°,则∠2= °.
9.如图,一个宽为2 cm的刻度尺(刻度单位: cm)放在圆形玻璃杯的杯口上,另一边与杯口外沿两个交点处的读数恰好是3和9,则玻璃杯的杯口外沿半径为 cm.
10.如图,四边形ABCD是☉O的内接四边形,∠ADC=150°,弦AC=2,则☉O的半径为 .
11.如图,AB、CD是半径为5的☉O的两条弦,AB=8,CD=6,MN是直径,AB⊥MN于点E,CD⊥MN于点F,P为EF上的任意一点,则PA+PC的最小值为 .
三、解答题(共45分)
12.(9分)(2024武威凉州区期末)如图所示,在☉O的内接四边形ABCD中,AB=AD,∠C=100°.若点E在上,求∠E的度数.
13.(12分)如图,AB是☉O的直径,BC是弦,OD⊥BC于点E,交☉O于点D,连结AC、BD.
(1)请写出五个不同类型的正确结论;
(2)若BC=8,ED=2,求☉O的半径.
14.(12分)如图1,AD、BC是☉O的弦,且AD=BC,连结AB、CD.
(1)求证:AB=CD;
(2)如图2,连结BD,若,BD=24,AB=4,求☉O的半径.
图1 图2
15.(12分)(2024渭南蒲城县模拟)如图,AB是☉O的直径,以AB为腰作等腰三角形ABC,底边BC交☉O于点D,连结AD,延长CA交☉O于点E,连结BE、DE.
(1)求证:∠CAD=∠BED;
(2)若BD=20,tan∠BDE=,求☉O的半径.
【详解答案】
1.B 2.B 3.A 4.C
5.C 解析:对于直线y=kx+2k-4,
当x=-2时,y=-4,
故直线y=kx+2k-4恒经过点(-2,-4),记为点D.
由于过圆内定点D的所有弦中,与OD垂直的弦最短,即当BD⊥OD时,BC最短,连结OB,OD,如图所示,
∵D(-2,-4),
∴OD==2.
∵☉O经过点(0,10),
∴OB=10.
∴BD==4.
∵BD⊥OD,
∴BC=2BD=8.
∴弦BC的最小值是8.
故选C.
6.A 解析:如图,连结AC,
∵在☉O中,AB是直径,
∴∠C=90°.
∵AB=5,BC=3,
∴AC==4.
∵点P是上任意一点.
∴4≤AP≤5.
故选A.
7.20° 8.35
9. 解析:∵杯口外沿两个交点处的读数恰好是3和9,∴AC=9-3=6(cm).
如图,设圆心为O,连结OA,过点O作OB⊥AC于点B,
则AB=AC=×6=3(cm).
设杯口的半径为r,则OB=r-2,OA=r,
在Rt△AOB中,OA2=OB2+AB2,即r2=(r-2)2+32,
解得r=.
10.2
解析:如图,连结OA、OC,∵四边形ABCD是☉O的内接四边形,
∴∠ADC+∠ABC=180°.∵∠ADC=150°,∴∠ABC=30°.∴∠AOC=2∠ABC=60°.
∵OA=OC,∴△OAC为等边三角形.
∴OA=AC=2,即☉O的半径为2.
11.7 解析:如图,连结OA、OB、OC、BC,作CH⊥AB于点H.
根据垂径定理得到BE=AB=4,CF=CD=3,
∴OE==3,
OF==4.
∴CH=OE+OF=3+4=7,
BH=BE+EH=BE+CF=4+3=7,
在Rt△BCH中,根据勾股定理,得BC=7,
则PA+PC的最小值为7.
12.解:如图,连结BD,
∵四边形ABCD是圆内接四边形,
∴∠C+∠BAD=180°.
∴∠BAD=180°-100°=80°.
∵AB=AD,
∴∠ABD=∠ADB.
∴∠ABD=×(180°-80°)=50°.
∵四边形ABDE为圆的内接四边形,
∴∠E+∠ABD=180°.
∴∠E=180°-50°=130°.
13.解:(1)正确的结论:CE=BE,,OE=AC,∠C=90°,AC∥OD.(答案不唯一)
(2)∵OD⊥BC,OD过圆心O,BC=8,
∴∠OEB=90°,BE=CE=4.
设☉O的半径为R,则OB=OD=R,
由勾股定理,得OB2=OE2+BE2,
即R2=(R-2)2+42,
解得R=5,即☉O的半径是5.
14.(1)证明:∵AD=BC,
∴.
∴,
即.
∴AB=CD.
(2)解:如图,过点O作OE⊥BD于点E,交☉O于点F,连结OB、BF,
∴,,BE=DE=12.
∵,∴.
∴AB=BF=4.∴在Rt△BEF中,EF==8.
设☉O的半径为r,则OE=r-8,
根据勾股定理,得122+(r-8)2=r2,
解得r=13,即☉O的半径为13.
15.(1)证明:∵AB是☉O的直径,
∴∠ADB=90°,
∴AD⊥BC.
∵AB=AC,
∴∠CAD=∠BAD,BD=CD.
∵∠BED=∠BAD,
∴∠CAD=∠BED.
(2)解:∵∠BDE=∠BAE,
∴tan∠BDE=tan∠BAE=.
∵AB是☉O的直径,
∴∠AEB=90°.
∴.
设AE=7x,则BE=24x,
∴AB==25x.
∴AC=AB=25x.
∴CE=AC+AE=32x.
∵BD=CD,BD=20,
∴BC=2BD=40.
在Rt△BCE中,BC2=CE2+BE2,
∴402=(32x)2+(24x)2.
解得x=1(负值已舍),
∴AB=25.
∴☉O的半径长为.
(时间:45分钟 满分:100分)
一、选择题(每小题5分,共30分)
1.下列说法中,结论错误的是 ( )
A.直径相等的两个圆是等圆
B.长度相等的两条弧是等弧
C.圆中最长的弦是直径
D.一条弦把圆分成两条弧,这两条弧可能是等弧
2.如图,已知☉O的半径为13,弦AB的长为24,则点O到AB的距离是 ( )
A.6 B.5
C.4 D.3
3.如图,已知AB是☉O的直径,CD是弦,若∠BCD=36°,则∠ABD等于 ( )
A.54° B.56°
C.64° D.66°
4.如图,CD是☉O的直径,弦AB⊥CD于点E,连结BC、BD,下列结论中不一定正确的是 ( )
A.AE=BE B.
C.OE=DE D.∠DBC=90°
5.如图,在平面直角坐标系中,☉O经过点(0,10),直线y=kx+2k-4与☉O交于B、C两点,则弦BC的最小值是 ( )
A.6 B.10 C.8 D.以上都不对
6.如图,在☉O中,AB是直径,BC是弦,点P是上任意一点.若AB=5,BC=3,则AP的长不可能为 ( )
A.3 B.4 C. D.5
二、填空题(每小题5分,共25分)
7.如图,延长☉O的弦AB、半径OC交于点D,BD=OA.若∠AOC=120°,则∠D的度数是 .
8.如图,AB是☉O的直径,点C、D、E都在☉O上,∠1=55°,则∠2= °.
9.如图,一个宽为2 cm的刻度尺(刻度单位: cm)放在圆形玻璃杯的杯口上,另一边与杯口外沿两个交点处的读数恰好是3和9,则玻璃杯的杯口外沿半径为 cm.
10.如图,四边形ABCD是☉O的内接四边形,∠ADC=150°,弦AC=2,则☉O的半径为 .
11.如图,AB、CD是半径为5的☉O的两条弦,AB=8,CD=6,MN是直径,AB⊥MN于点E,CD⊥MN于点F,P为EF上的任意一点,则PA+PC的最小值为 .
三、解答题(共45分)
12.(9分)(2024武威凉州区期末)如图所示,在☉O的内接四边形ABCD中,AB=AD,∠C=100°.若点E在上,求∠E的度数.
13.(12分)如图,AB是☉O的直径,BC是弦,OD⊥BC于点E,交☉O于点D,连结AC、BD.
(1)请写出五个不同类型的正确结论;
(2)若BC=8,ED=2,求☉O的半径.
14.(12分)如图1,AD、BC是☉O的弦,且AD=BC,连结AB、CD.
(1)求证:AB=CD;
(2)如图2,连结BD,若,BD=24,AB=4,求☉O的半径.
图1 图2
15.(12分)(2024渭南蒲城县模拟)如图,AB是☉O的直径,以AB为腰作等腰三角形ABC,底边BC交☉O于点D,连结AD,延长CA交☉O于点E,连结BE、DE.
(1)求证:∠CAD=∠BED;
(2)若BD=20,tan∠BDE=,求☉O的半径.
【详解答案】
1.B 2.B 3.A 4.C
5.C 解析:对于直线y=kx+2k-4,
当x=-2时,y=-4,
故直线y=kx+2k-4恒经过点(-2,-4),记为点D.
由于过圆内定点D的所有弦中,与OD垂直的弦最短,即当BD⊥OD时,BC最短,连结OB,OD,如图所示,
∵D(-2,-4),
∴OD==2.
∵☉O经过点(0,10),
∴OB=10.
∴BD==4.
∵BD⊥OD,
∴BC=2BD=8.
∴弦BC的最小值是8.
故选C.
6.A 解析:如图,连结AC,
∵在☉O中,AB是直径,
∴∠C=90°.
∵AB=5,BC=3,
∴AC==4.
∵点P是上任意一点.
∴4≤AP≤5.
故选A.
7.20° 8.35
9. 解析:∵杯口外沿两个交点处的读数恰好是3和9,∴AC=9-3=6(cm).
如图,设圆心为O,连结OA,过点O作OB⊥AC于点B,
则AB=AC=×6=3(cm).
设杯口的半径为r,则OB=r-2,OA=r,
在Rt△AOB中,OA2=OB2+AB2,即r2=(r-2)2+32,
解得r=.
10.2
解析:如图,连结OA、OC,∵四边形ABCD是☉O的内接四边形,
∴∠ADC+∠ABC=180°.∵∠ADC=150°,∴∠ABC=30°.∴∠AOC=2∠ABC=60°.
∵OA=OC,∴△OAC为等边三角形.
∴OA=AC=2,即☉O的半径为2.
11.7 解析:如图,连结OA、OB、OC、BC,作CH⊥AB于点H.
根据垂径定理得到BE=AB=4,CF=CD=3,
∴OE==3,
OF==4.
∴CH=OE+OF=3+4=7,
BH=BE+EH=BE+CF=4+3=7,
在Rt△BCH中,根据勾股定理,得BC=7,
则PA+PC的最小值为7.
12.解:如图,连结BD,
∵四边形ABCD是圆内接四边形,
∴∠C+∠BAD=180°.
∴∠BAD=180°-100°=80°.
∵AB=AD,
∴∠ABD=∠ADB.
∴∠ABD=×(180°-80°)=50°.
∵四边形ABDE为圆的内接四边形,
∴∠E+∠ABD=180°.
∴∠E=180°-50°=130°.
13.解:(1)正确的结论:CE=BE,,OE=AC,∠C=90°,AC∥OD.(答案不唯一)
(2)∵OD⊥BC,OD过圆心O,BC=8,
∴∠OEB=90°,BE=CE=4.
设☉O的半径为R,则OB=OD=R,
由勾股定理,得OB2=OE2+BE2,
即R2=(R-2)2+42,
解得R=5,即☉O的半径是5.
14.(1)证明:∵AD=BC,
∴.
∴,
即.
∴AB=CD.
(2)解:如图,过点O作OE⊥BD于点E,交☉O于点F,连结OB、BF,
∴,,BE=DE=12.
∵,∴.
∴AB=BF=4.∴在Rt△BEF中,EF==8.
设☉O的半径为r,则OE=r-8,
根据勾股定理,得122+(r-8)2=r2,
解得r=13,即☉O的半径为13.
15.(1)证明:∵AB是☉O的直径,
∴∠ADB=90°,
∴AD⊥BC.
∵AB=AC,
∴∠CAD=∠BAD,BD=CD.
∵∠BED=∠BAD,
∴∠CAD=∠BED.
(2)解:∵∠BDE=∠BAE,
∴tan∠BDE=tan∠BAE=.
∵AB是☉O的直径,
∴∠AEB=90°.
∴.
设AE=7x,则BE=24x,
∴AB==25x.
∴AC=AB=25x.
∴CE=AC+AE=32x.
∵BD=CD,BD=20,
∴BC=2BD=40.
在Rt△BCE中,BC2=CE2+BE2,
∴402=(32x)2+(24x)2.
解得x=1(负值已舍),
∴AB=25.
∴☉O的半径长为.
