27.1.1.圆的基本元素 课时作业(含答案) 2024-2025学年数学华东师大版九年级下册
文档属性
| 名称 | 27.1.1.圆的基本元素 课时作业(含答案) 2024-2025学年数学华东师大版九年级下册 | 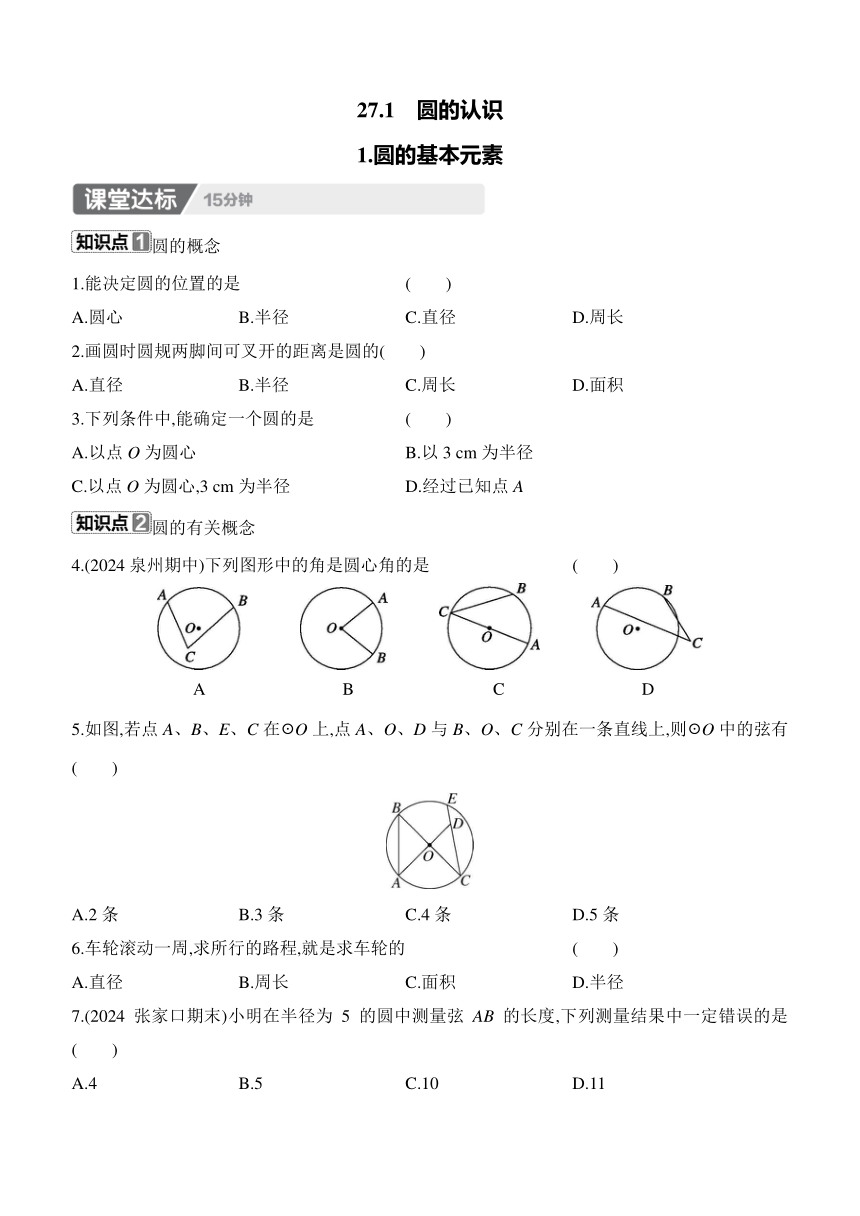 | |
| 格式 | docx | ||
| 文件大小 | 202.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-26 21:36:38 | ||
图片预览


文档简介
27.1 圆的认识
1.圆的基本元素
圆的概念
1.能决定圆的位置的是 ( )
A.圆心 B.半径 C.直径 D.周长
2.画圆时圆规两脚间可叉开的距离是圆的( )
A.直径 B.半径 C.周长 D.面积
3.下列条件中,能确定一个圆的是 ( )
A.以点O为圆心 B.以3 cm为半径
C.以点O为圆心,3 cm为半径 D.经过已知点A
圆的有关概念
4.(2024泉州期中)下列图形中的角是圆心角的是 ( )
A B C D
5.如图,若点A、B、E、C在☉O上,点A、O、D与B、O、C分别在一条直线上,则☉O中的弦有 ( )
A.2条 B.3条 C.4条 D.5条
6.车轮滚动一周,求所行的路程,就是求车轮的 ( )
A.直径 B.周长 C.面积 D.半径
7.(2024张家口期末)小明在半径为5的圆中测量弦AB的长度,下列测量结果中一定错误的是 ( )
A.4 B.5 C.10 D.11
8.如图,AB为☉O的直径,点C、D在☉O上,若已知∠BOC=70°,AD∥OC,则圆心角∠AOD的度数为 .
1.下列说法中,正确的是 ( )
A.过圆心的直线是圆的直径 B.直径是圆中最长的弦
C.相等长度的两条弧是等弧 D.小于半圆的弧叫做优弧
2.如图所示,点M是☉O上的任意一点,下列结论:
①以M为端点的弦只有一条;②以M为端点的半径只有一条;③以M为端点的直径只有一条;④以M为端点的弧只有一条.
其中,正确的有 ( )
A.1个 B.2个 C.3个 D.4个
3.(易错题)如图,AB、CD是☉O的两条相互垂直的直径,点E是☉O上的动点(点E不与点A、B、C、D重合),过点E作EF⊥AB于点F,EG⊥CD于点G,连结FG,FG的中点为P.若点E在圆周上运动一周,下列结论错误的是 ( )
A.FG的长不变
B.点P到点O的距离不变
C.点P到点E的距离不变
D.点P到AB、CD的距离不变
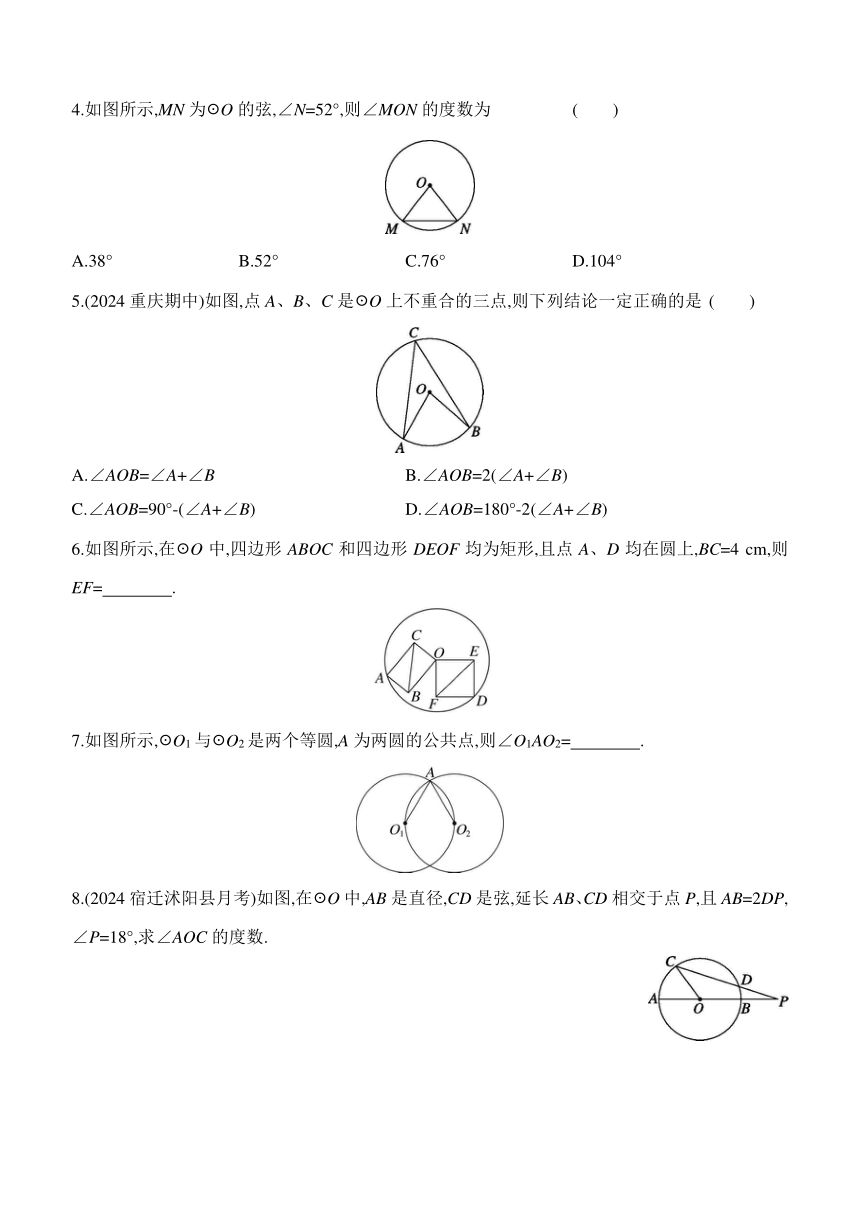
4.如图所示,MN为☉O的弦,∠N=52°,则∠MON的度数为 ( )
A.38° B.52° C.76° D.104°
5.(2024重庆期中)如图,点A、B、C是☉O上不重合的三点,则下列结论一定正确的是 ( )
A.∠AOB=∠A+∠B B.∠AOB=2(∠A+∠B)
C.∠AOB=90°-(∠A+∠B) D.∠AOB=180°-2(∠A+∠B)
6.如图所示,在☉O中,四边形ABOC和四边形DEOF均为矩形,且点A、D均在圆上,BC=4 cm,则EF= .
7.如图所示,☉O1与☉O2是两个等圆,A为两圆的公共点,则∠O1AO2= .
8.(2024宿迁沭阳县月考)如图,在☉O中,AB是直径,CD是弦,延长AB、CD相交于点P,且AB=2DP,∠P=18°,求∠AOC的度数.
9.(几何直观)如图,直线AB经过☉O的圆心,与☉O相交于点A、B,点C在☉O上,且∠AOC=30°,点P是直线AB上的一个动点(与O不重合),直线PC与☉O相交于点Q,问:点P在直线AB的什么位置上时,QP=QO 这样的点P共有几个 并相应地求出∠OCP的度数.
【详解答案】
课堂达标
1.A 2.B 3.C 4.B 5.B 6.B 7.D
8.40°
课后提升
1.B 解析:过圆心的弦是圆的直径,故A不符合题意;直径是圆中最长的弦,故B符合题意;在同圆或等圆中,能够互相重合的弧叫做等弧,故C不符合题意;小于半圆的弧叫做劣弧,故D不符合题意.故选B.
2.B 解析:以M为端点的弦有无数条,所以①错误;②正确;③正确;以M为端点的弧有无数条,所以④错误.故选B.
3.D 解析:由题意知,四边形OFEG是矩形,连结OE(图略),则OE=FG,点P为OE与FG的交点,OP=EP=FP=GP.在点E运动的过程中,OE的长不变,则FG的长不变,OP、EP的长不变;在点E运动的过程中,点P到AB、CD的距离是变化的.故选D.
4.C 解析:∵OM=ON,∴∠M=∠N=52°.∴∠MON=180°-2×52°=76°.故选C.
5.B 解析:连结CO并延长交☉O于D,如图所示.
∵OA=OB=OC,
∴∠A=∠OCA,∠B=∠OCB.
∴∠AOD=∠A+∠OCA=2∠A,
∠BOD=∠B+∠OCB=2∠B.
∴∠AOD+∠BOD=2(∠A+∠B),
即∠AOB=2(∠A+∠B).
故选B.
6.4 cm 解析:如图所示,连结OA、OD,由矩形的性质可知OA=BC,OD=EF.∵OA=OD,∴EF=BC=4 cm.
7.60° 解析:连结O1O2(图略),则△O1O2A是等边三角形,
∴∠O1AO2=60°.
8.解:如图,连结OD,
∵AB=2DP=2OD,∠P=18°,
∴OD=DP.∴∠DOP=∠P=18°.
∵∠ODC是△OPD的外角,
∴∠ODC=∠P+∠DOP=18°+18°=36°.
∵OD=OC,
∴∠OCD=∠ODC=36°.
∴∠COD=180°-36°-36°=108°.
∴∠AOC=180°-∠COD-∠DOP=180°-108°-18°=54°.
9.解:(1)根据题意,当点P在线段OA上时,如图1,
图1
在△QOC中,OC=OQ,
∴∠OQC=∠OCQ.
在△OPQ中,QP=QO,
∴∠QOP=∠QPO.
又∵∠QPO=∠OCQ+∠AOC,∠AOC=30°,∠QOP+∠QPO+∠OQC=180°,
∴3∠OCP=120°,∴∠OCP=40°.
(2)当P在线段OA的延长线上时,如图2.
图2
∵OC=OQ,
∴∠OQP=①.
∵QP=QO,
∴∠OPQ=②,
在△OQP中,30°+∠QOC+∠OQP+∠OPQ=180°③,
把①②代入③,得∠QOC=20°,则∠OQP=80°,
∴∠OCP=100°.
(3)当P在线段OA的反向延长线上时,如图3.
图3
∵OC=OQ,
∴∠OCP=∠OQC=①.
∵∠AOC=30°,
∴∠COQ+∠POQ=150°②.
∵QP=QO,∴∠OPQ=∠POQ,
∴2∠OPQ=∠OCP=∠OQC③.
①②③联立,得∠OPQ=10°,
∴∠OCP=20°.
综上所述,点P共有3个,∠OCP的度数分别是40°或100°或20°.
1.圆的基本元素
圆的概念
1.能决定圆的位置的是 ( )
A.圆心 B.半径 C.直径 D.周长
2.画圆时圆规两脚间可叉开的距离是圆的( )
A.直径 B.半径 C.周长 D.面积
3.下列条件中,能确定一个圆的是 ( )
A.以点O为圆心 B.以3 cm为半径
C.以点O为圆心,3 cm为半径 D.经过已知点A
圆的有关概念
4.(2024泉州期中)下列图形中的角是圆心角的是 ( )
A B C D
5.如图,若点A、B、E、C在☉O上,点A、O、D与B、O、C分别在一条直线上,则☉O中的弦有 ( )
A.2条 B.3条 C.4条 D.5条
6.车轮滚动一周,求所行的路程,就是求车轮的 ( )
A.直径 B.周长 C.面积 D.半径
7.(2024张家口期末)小明在半径为5的圆中测量弦AB的长度,下列测量结果中一定错误的是 ( )
A.4 B.5 C.10 D.11
8.如图,AB为☉O的直径,点C、D在☉O上,若已知∠BOC=70°,AD∥OC,则圆心角∠AOD的度数为 .
1.下列说法中,正确的是 ( )
A.过圆心的直线是圆的直径 B.直径是圆中最长的弦
C.相等长度的两条弧是等弧 D.小于半圆的弧叫做优弧
2.如图所示,点M是☉O上的任意一点,下列结论:
①以M为端点的弦只有一条;②以M为端点的半径只有一条;③以M为端点的直径只有一条;④以M为端点的弧只有一条.
其中,正确的有 ( )
A.1个 B.2个 C.3个 D.4个
3.(易错题)如图,AB、CD是☉O的两条相互垂直的直径,点E是☉O上的动点(点E不与点A、B、C、D重合),过点E作EF⊥AB于点F,EG⊥CD于点G,连结FG,FG的中点为P.若点E在圆周上运动一周,下列结论错误的是 ( )
A.FG的长不变
B.点P到点O的距离不变
C.点P到点E的距离不变
D.点P到AB、CD的距离不变
4.如图所示,MN为☉O的弦,∠N=52°,则∠MON的度数为 ( )
A.38° B.52° C.76° D.104°
5.(2024重庆期中)如图,点A、B、C是☉O上不重合的三点,则下列结论一定正确的是 ( )
A.∠AOB=∠A+∠B B.∠AOB=2(∠A+∠B)
C.∠AOB=90°-(∠A+∠B) D.∠AOB=180°-2(∠A+∠B)
6.如图所示,在☉O中,四边形ABOC和四边形DEOF均为矩形,且点A、D均在圆上,BC=4 cm,则EF= .
7.如图所示,☉O1与☉O2是两个等圆,A为两圆的公共点,则∠O1AO2= .
8.(2024宿迁沭阳县月考)如图,在☉O中,AB是直径,CD是弦,延长AB、CD相交于点P,且AB=2DP,∠P=18°,求∠AOC的度数.
9.(几何直观)如图,直线AB经过☉O的圆心,与☉O相交于点A、B,点C在☉O上,且∠AOC=30°,点P是直线AB上的一个动点(与O不重合),直线PC与☉O相交于点Q,问:点P在直线AB的什么位置上时,QP=QO 这样的点P共有几个 并相应地求出∠OCP的度数.
【详解答案】
课堂达标
1.A 2.B 3.C 4.B 5.B 6.B 7.D
8.40°
课后提升
1.B 解析:过圆心的弦是圆的直径,故A不符合题意;直径是圆中最长的弦,故B符合题意;在同圆或等圆中,能够互相重合的弧叫做等弧,故C不符合题意;小于半圆的弧叫做劣弧,故D不符合题意.故选B.
2.B 解析:以M为端点的弦有无数条,所以①错误;②正确;③正确;以M为端点的弧有无数条,所以④错误.故选B.
3.D 解析:由题意知,四边形OFEG是矩形,连结OE(图略),则OE=FG,点P为OE与FG的交点,OP=EP=FP=GP.在点E运动的过程中,OE的长不变,则FG的长不变,OP、EP的长不变;在点E运动的过程中,点P到AB、CD的距离是变化的.故选D.
4.C 解析:∵OM=ON,∴∠M=∠N=52°.∴∠MON=180°-2×52°=76°.故选C.
5.B 解析:连结CO并延长交☉O于D,如图所示.
∵OA=OB=OC,
∴∠A=∠OCA,∠B=∠OCB.
∴∠AOD=∠A+∠OCA=2∠A,
∠BOD=∠B+∠OCB=2∠B.
∴∠AOD+∠BOD=2(∠A+∠B),
即∠AOB=2(∠A+∠B).
故选B.
6.4 cm 解析:如图所示,连结OA、OD,由矩形的性质可知OA=BC,OD=EF.∵OA=OD,∴EF=BC=4 cm.
7.60° 解析:连结O1O2(图略),则△O1O2A是等边三角形,
∴∠O1AO2=60°.
8.解:如图,连结OD,
∵AB=2DP=2OD,∠P=18°,
∴OD=DP.∴∠DOP=∠P=18°.
∵∠ODC是△OPD的外角,
∴∠ODC=∠P+∠DOP=18°+18°=36°.
∵OD=OC,
∴∠OCD=∠ODC=36°.
∴∠COD=180°-36°-36°=108°.
∴∠AOC=180°-∠COD-∠DOP=180°-108°-18°=54°.
9.解:(1)根据题意,当点P在线段OA上时,如图1,
图1
在△QOC中,OC=OQ,
∴∠OQC=∠OCQ.
在△OPQ中,QP=QO,
∴∠QOP=∠QPO.
又∵∠QPO=∠OCQ+∠AOC,∠AOC=30°,∠QOP+∠QPO+∠OQC=180°,
∴3∠OCP=120°,∴∠OCP=40°.
(2)当P在线段OA的延长线上时,如图2.
图2
∵OC=OQ,
∴∠OQP=①.
∵QP=QO,
∴∠OPQ=②,
在△OQP中,30°+∠QOC+∠OQP+∠OPQ=180°③,
把①②代入③,得∠QOC=20°,则∠OQP=80°,
∴∠OCP=100°.
(3)当P在线段OA的反向延长线上时,如图3.
图3
∵OC=OQ,
∴∠OCP=∠OQC=①.
∵∠AOC=30°,
∴∠COQ+∠POQ=150°②.
∵QP=QO,∴∠OPQ=∠POQ,
∴2∠OPQ=∠OCP=∠OQC③.
①②③联立,得∠OPQ=10°,
∴∠OCP=20°.
综上所述,点P共有3个,∠OCP的度数分别是40°或100°或20°.
