27.2.1.点与圆的位置关系 课时作业(含答案) 2024-2025学年数学华东师大版九年级下册
文档属性
| 名称 | 27.2.1.点与圆的位置关系 课时作业(含答案) 2024-2025学年数学华东师大版九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 238.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-26 21:36:36 | ||
图片预览


文档简介
27.2 与圆有关的位置关系
1.点与圆的位置关系
点与圆的位置关系
1.已知☉O的半径OA的长为,OB=,则下列图形正确的是 ( )
A B C D
2.(2024定西期末)已知☉P的半径为4,圆心P的坐标为(-3,4),则平面直角坐标系的原点O在☉P .(填“上”“内”或“外”)
3.在△ABC中,∠C=90°,AC=2,BC=3,M为AB的中点.
(1)若以点C为圆心,2为半径作☉C,试判断点A、B、M与☉C的位置关系;
(2)若以点C为圆心作☉C,要使A、B、M三点中至少有一点在☉C内,且至少有一点在☉C外,则☉C的半径r的取值范围是多少
过已知点作圆
4.下列条件中不一定能确定一个圆的是 ( )
A.圆心和半径 B.直径
C.三角形的三个顶点 D.平面上的三个已知点
5.(易错题)若点A、B、C在同一条直线上,点D在直线AB外,则过这四点中的任意三个点,能画圆的个数是 ( )
A.1 B.2 C.3 D.4
三角形的外接圆
6.三角形的外心具有的性质是 ( )
A.到三边的距离相等 B.到三个顶点的距离相等
C.外心在三角形外 D.外心在三角形内
7.如图,在平面直角坐标系xOy中,点A(4,0),B(3,3),点P是△OAB的外接圆的圆心,则点P的坐标为 .
1.小明不慎把家里的圆形镜子打碎了,其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的一块碎片应该是 ( )
A.第①块 B.第②块 C.第③块 D.第④块
2.若一个三角形两边的长分别是8和6,第三边的长是方程x2-12x+20=0的一个实数根,则这个三角形的外接圆的半径是 ( )
A.4 B.5 C.6 D.8
3.(2024石家庄期末)如图,在5×5的正方形网格中,一条圆弧经过A、B、C三点,那么点M在这条圆弧所在圆的 ( )
A.内部 B.外部
C.圆上 D.不能确定
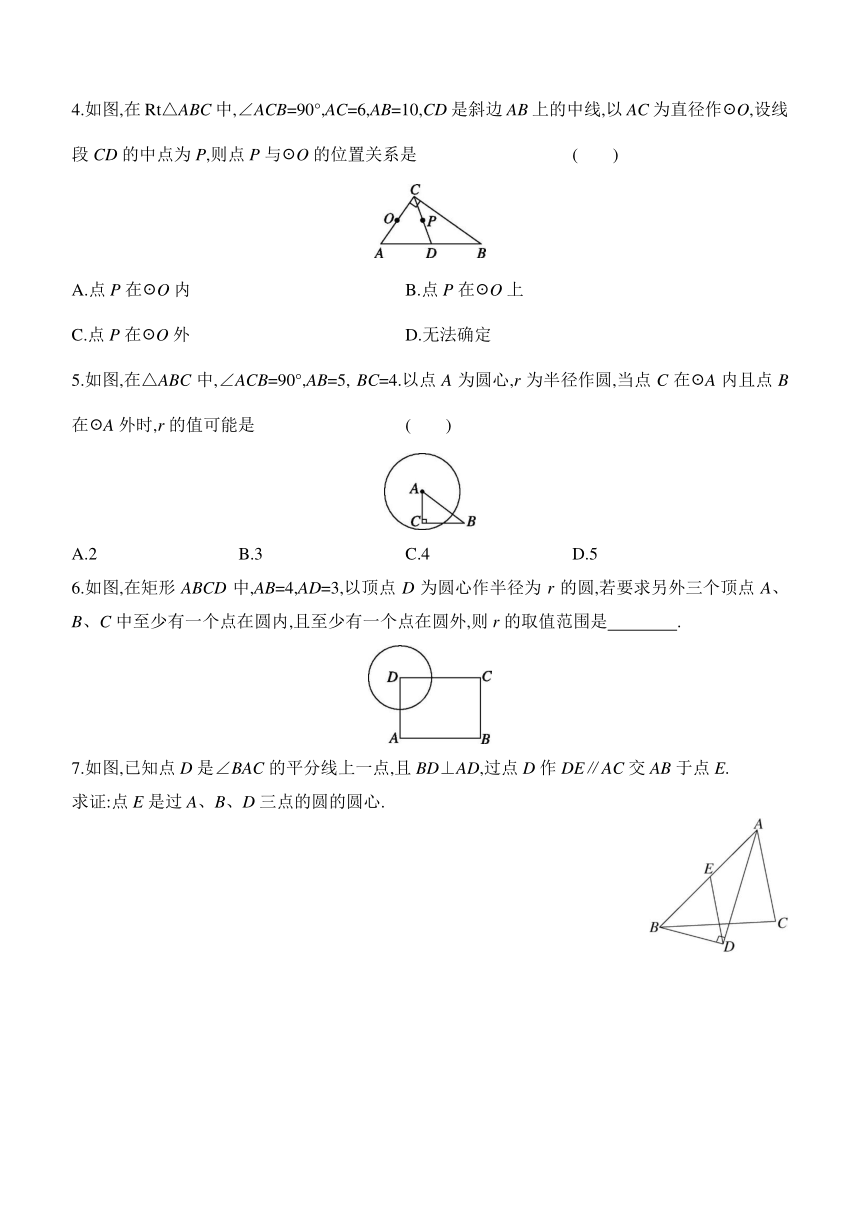
4.如图,在Rt△ABC中,∠ACB=90°,AC=6,AB=10,CD是斜边AB上的中线,以AC为直径作☉O,设线段CD的中点为P,则点P与☉O的位置关系是 ( )
A.点P在☉O内 B.点P在☉O上
C.点P在☉O外 D.无法确定
5.如图,在△ABC中,∠ACB=90°,AB=5, BC=4.以点A为圆心,r为半径作圆,当点C在☉A内且点B在☉A外时,r的值可能是 ( )
A.2 B.3 C.4 D.5
6.如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若要求另外三个顶点A、B、C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是 .
7.如图,已知点D是∠BAC的平分线上一点,且BD⊥AD,过点D作DE∥AC交AB于点E.
求证:点E是过A、B、D三点的圆的圆心.
8.(推理能力)如图,△ABC是☉O的内接三角形,直径HF交AC于点D,HF、BC的延长线交于点E.
(1)若HF⊥AB,求证:∠OAD=∠E;
(2)若A点是下半圆上一动点,当点A运动到什么位置时,△CDE的外心在△CDE的一边上 请简述理由.
【详解答案】
课堂达标
1.A 2.外
3.解:(1)在△ABC中,∵∠C=90°,AC=2,BC=3,AB的中点为M,
∴AB=,
CM=AB=.以点C为圆心,2为半径作☉C,
∵AC=2,∴点A在圆上.∵CM=<2,∴点M在圆内.∵BC=3>2,∴点B在圆外.
(2)以点C为圆心作☉C,使A、B、M三点中至少有一点在☉C内时,r>,当至少有一点在☉C外时,r<3,故☉C的半径r的取值范围为4.D 5.C 6.B 7.(2,1)
课后提升
1.A 解析:第①块出现一段完整的弧,可在这段弧上任作两条弦,作出这两条弦的垂直平分线,两条垂直平分线的交点就是圆心,进而可得到半径的长.故选A.
2.B 解析:解方程x2-12x+20=0,得x=10或2.当x=2时,2+6=8,不符合题意,∴x=10,即第三边长为10.∵62+82=102,∴这个三角形是直角三角形,∴这个三角形的外接圆的半径为5.故选B.
3.C 解析:如图,线段AB的垂直平分线和线段BC的垂直平分线的交点O即为圆心,连结OC、OM,
则OC=,
OM=,
∴OC=OM.
∴点M在这条圆弧所在圆的圆上.
故选C.
4.A 解析:连结OP(图略),∵AC=6,AB=10,CD是斜边AB上的中线,∴AD=5.∵点O是AC的中点,点P是CD的中点,∴OP是△CAD的中位线,OC=OA=3,OP=AD=2.5.∴OP5.C 解析:∵在△ABC中,∠ACB=90°,AB=5,BC=4,∴AC==3.∵点C在☉A内且点B在☉A外,∴AC6.37.证明:如图,∵点D在∠BAC的平分线上,∴∠1=∠2.
∵DE∥AC,
∴∠1=∠3.
∴∠2=∠3.
∴AE=DE.
∵BD⊥AD于点D,
∴∠ADB=90°.
∴∠EBD+∠2=∠EDB+∠3=90°.
∴∠EBD=∠EDB.∴BE=DE.
∴AE=BE=DE.
∴点E是过A、B、D三点的圆的圆心.
8.(1)证明:如图,连结OB,
∵HF⊥AB,∴.
∴∠AOH=∠ACB=∠AOB.
∵∠AOD+∠AOH=180°,
∠ECD+∠ACB=180°,
∴∠AOD=∠ECD.
∵∠ODA=∠CDE,∴∠OAD=∠E.
(2)解:当AB是直径或AC⊥HF时,△CDE的外心在△CDE的一边上.理由如下:
①当AB是直径时,∠ACB=90°,∴∠DCE=90°,即△CDE是直角三角形,∴△CDE的外心在△CDE的边DE上;
②当A运动到使AC⊥HF时,△CDE是直角三角形,此时△CDE的外心在△CDE的边CE上.
综上所述,当AB是直径或AC⊥HF时,△CDE的外心在△CDE的一边上.
1.点与圆的位置关系
点与圆的位置关系
1.已知☉O的半径OA的长为,OB=,则下列图形正确的是 ( )
A B C D
2.(2024定西期末)已知☉P的半径为4,圆心P的坐标为(-3,4),则平面直角坐标系的原点O在☉P .(填“上”“内”或“外”)
3.在△ABC中,∠C=90°,AC=2,BC=3,M为AB的中点.
(1)若以点C为圆心,2为半径作☉C,试判断点A、B、M与☉C的位置关系;
(2)若以点C为圆心作☉C,要使A、B、M三点中至少有一点在☉C内,且至少有一点在☉C外,则☉C的半径r的取值范围是多少
过已知点作圆
4.下列条件中不一定能确定一个圆的是 ( )
A.圆心和半径 B.直径
C.三角形的三个顶点 D.平面上的三个已知点
5.(易错题)若点A、B、C在同一条直线上,点D在直线AB外,则过这四点中的任意三个点,能画圆的个数是 ( )
A.1 B.2 C.3 D.4
三角形的外接圆
6.三角形的外心具有的性质是 ( )
A.到三边的距离相等 B.到三个顶点的距离相等
C.外心在三角形外 D.外心在三角形内
7.如图,在平面直角坐标系xOy中,点A(4,0),B(3,3),点P是△OAB的外接圆的圆心,则点P的坐标为 .
1.小明不慎把家里的圆形镜子打碎了,其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的一块碎片应该是 ( )
A.第①块 B.第②块 C.第③块 D.第④块
2.若一个三角形两边的长分别是8和6,第三边的长是方程x2-12x+20=0的一个实数根,则这个三角形的外接圆的半径是 ( )
A.4 B.5 C.6 D.8
3.(2024石家庄期末)如图,在5×5的正方形网格中,一条圆弧经过A、B、C三点,那么点M在这条圆弧所在圆的 ( )
A.内部 B.外部
C.圆上 D.不能确定
4.如图,在Rt△ABC中,∠ACB=90°,AC=6,AB=10,CD是斜边AB上的中线,以AC为直径作☉O,设线段CD的中点为P,则点P与☉O的位置关系是 ( )
A.点P在☉O内 B.点P在☉O上
C.点P在☉O外 D.无法确定
5.如图,在△ABC中,∠ACB=90°,AB=5, BC=4.以点A为圆心,r为半径作圆,当点C在☉A内且点B在☉A外时,r的值可能是 ( )
A.2 B.3 C.4 D.5
6.如图,在矩形ABCD中,AB=4,AD=3,以顶点D为圆心作半径为r的圆,若要求另外三个顶点A、B、C中至少有一个点在圆内,且至少有一个点在圆外,则r的取值范围是 .
7.如图,已知点D是∠BAC的平分线上一点,且BD⊥AD,过点D作DE∥AC交AB于点E.
求证:点E是过A、B、D三点的圆的圆心.
8.(推理能力)如图,△ABC是☉O的内接三角形,直径HF交AC于点D,HF、BC的延长线交于点E.
(1)若HF⊥AB,求证:∠OAD=∠E;
(2)若A点是下半圆上一动点,当点A运动到什么位置时,△CDE的外心在△CDE的一边上 请简述理由.
【详解答案】
课堂达标
1.A 2.外
3.解:(1)在△ABC中,∵∠C=90°,AC=2,BC=3,AB的中点为M,
∴AB=,
CM=AB=.以点C为圆心,2为半径作☉C,
∵AC=2,∴点A在圆上.∵CM=<2,∴点M在圆内.∵BC=3>2,∴点B在圆外.
(2)以点C为圆心作☉C,使A、B、M三点中至少有一点在☉C内时,r>,当至少有一点在☉C外时,r<3,故☉C的半径r的取值范围为
课后提升
1.A 解析:第①块出现一段完整的弧,可在这段弧上任作两条弦,作出这两条弦的垂直平分线,两条垂直平分线的交点就是圆心,进而可得到半径的长.故选A.
2.B 解析:解方程x2-12x+20=0,得x=10或2.当x=2时,2+6=8,不符合题意,∴x=10,即第三边长为10.∵62+82=102,∴这个三角形是直角三角形,∴这个三角形的外接圆的半径为5.故选B.
3.C 解析:如图,线段AB的垂直平分线和线段BC的垂直平分线的交点O即为圆心,连结OC、OM,
则OC=,
OM=,
∴OC=OM.
∴点M在这条圆弧所在圆的圆上.
故选C.
4.A 解析:连结OP(图略),∵AC=6,AB=10,CD是斜边AB上的中线,∴AD=5.∵点O是AC的中点,点P是CD的中点,∴OP是△CAD的中位线,OC=OA=3,OP=AD=2.5.∴OP
∵DE∥AC,
∴∠1=∠3.
∴∠2=∠3.
∴AE=DE.
∵BD⊥AD于点D,
∴∠ADB=90°.
∴∠EBD+∠2=∠EDB+∠3=90°.
∴∠EBD=∠EDB.∴BE=DE.
∴AE=BE=DE.
∴点E是过A、B、D三点的圆的圆心.
8.(1)证明:如图,连结OB,
∵HF⊥AB,∴.
∴∠AOH=∠ACB=∠AOB.
∵∠AOD+∠AOH=180°,
∠ECD+∠ACB=180°,
∴∠AOD=∠ECD.
∵∠ODA=∠CDE,∴∠OAD=∠E.
(2)解:当AB是直径或AC⊥HF时,△CDE的外心在△CDE的一边上.理由如下:
①当AB是直径时,∠ACB=90°,∴∠DCE=90°,即△CDE是直角三角形,∴△CDE的外心在△CDE的边DE上;
②当A运动到使AC⊥HF时,△CDE是直角三角形,此时△CDE的外心在△CDE的边CE上.
综上所述,当AB是直径或AC⊥HF时,△CDE的外心在△CDE的一边上.
