27.4 正多边形和圆 课时作业(含答案) 2024-2025学年数学华东师大版九年级下册
文档属性
| 名称 | 27.4 正多边形和圆 课时作业(含答案) 2024-2025学年数学华东师大版九年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 235.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-26 00:00:00 | ||
图片预览



文档简介
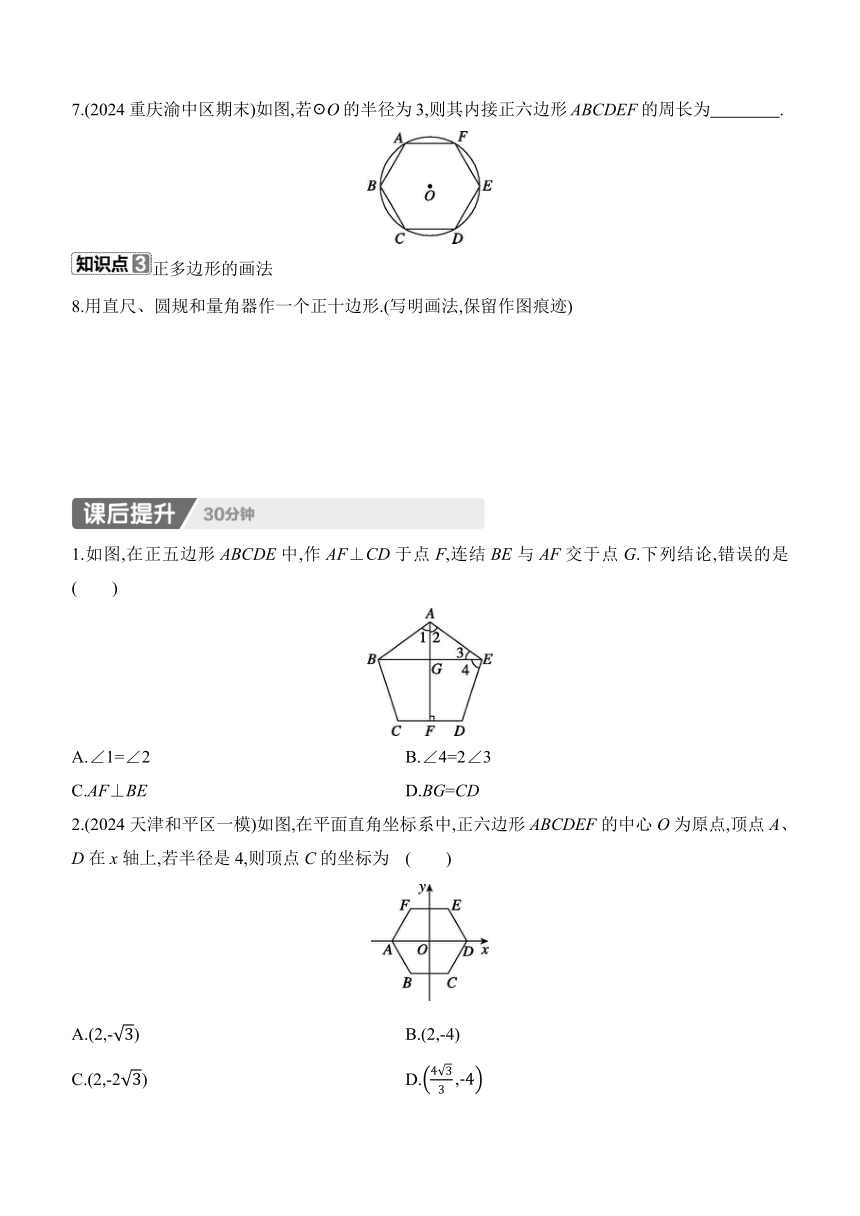
27.4 正多边形和圆
圆内接正多边形及相关定义
1.以下图形中,是正多边形的是 ( )
A.平行四边形 B.菱形 C.矩形 D.正方形
2.(易错题)给出下列说法:①各边相等的圆内接多边形是正多边形;②各边相等的圆外切多边形是正多边形;③各角相等的圆内接多边形是正多边形;④各角相等的圆外切多边形是正多边形.其中正确的是 ( )
A.①④ B.②③ C.①③ D.②④
3.内角和与外角和相等的正多边形的对称轴有 ( )
A.4条 B.6条 C.7条 D.8条
圆内接正多边形的相关计算
4.正八边形的一个中心角的度数是 ( )
A.30° B.45° C.60° D.90°
5.如图,正五边形ABCDE内接于☉O,CP与☉O相切于点C,则∠BCP的度数为 ( )
A.120° B.108° C.144° D.162°
6.(跨学科)苯分子的环状结构是由德国化学家凯库勒提出的.随着研究的不断深入,发现苯分子中的6个碳原子与6个氢原子均在同一平面内,且所有碳碳键的键长都相等(如图1),组成了一个完美的六边形(正六边形),图2是其平面示意图,则∠1的度数为 ( )
图1 图2
A.130° B.120° C.110° D.60°
7.(2024重庆渝中区期末)如图,若☉O的半径为3,则其内接正六边形ABCDEF的周长为 .
正多边形的画法
8.用直尺、圆规和量角器作一个正十边形.(写明画法,保留作图痕迹)
1.如图,在正五边形ABCDE中,作AF⊥CD于点F,连结BE与AF交于点G.下列结论,错误的是 ( )
A.∠1=∠2 B.∠4=2∠3
C.AF⊥BE D.BG=CD
2.(2024天津和平区一模)如图,在平面直角坐标系中,正六边形ABCDEF的中心O为原点,顶点A、D在x轴上,若半径是4,则顶点C的坐标为 ( )
A.(2,-) B.(2,-4)
C.(2,-2) D.
3.如图,有公共顶点O的两个边长为5的正五边形(不重叠),以点O为圆心,5为半径作弧,构成一个“蘑菇”形图案(阴影部分),则这个“蘑菇”形图案的周长为 ( )
A.4π B.4π+20
C.10π D.10π+20
4.如图,正六边形ABCDEF和正五边形AHIJK内接于☉O,且有公共顶点A,则∠BOH的度数为 °.
5.(2024上海虹口区二模)如图,已知正六边形螺帽的边长是4 cm,那么与该螺帽匹配的扳手的开口a为 cm.
6.如图,正六边形ABCDEF的顶点A、F分别在正方形BMGH的边BH、GH上.若正方形BMGH的边长为6,则正六边形ABCDEF的边长为 .
7.如图,A、B、C、D、E、F是正n边形的六个连续顶点,AE与CF交于点G,若∠EGF=30°,则n= .
8.如图,已知☉O和☉O上的一点A,请完成下列任务:
(1)用尺规作☉O的内接正六边形ABCDEF;
(2)连结BF、CE,判断四边形BCEF的形状并加以证明.
9.(推理能力)如图,正六边形ABCDEF内接于☉O,BE是☉O的直径,连结BF,延长BA,过F作FG⊥BA,垂足为G.
(1)求证:FG是☉O的切线;
(2)已知FG=2,求图中阴影部分的面积.
【详解答案】
课堂达标
1.D 2.A 3.A 4.B 5.C 6.B
7.18
8.解:如图所示,画法如下:
(1)任意作一个圆,记圆心为O.
(2)作圆心角∠A1OA2==36°.
(3)以A2为圆心,以弦A1A2为半径画弧交☉O于A3,依次作出A4,A5,…,A10.
(4)顺次连结点A1,A2,A3,…,A10,则十边形A1A2…A10为正十边形.
课后提升
1.D 解析:∵五边形ABCDE是正五边形,
∴AB=AE=BC=CD=DE,∠ABC=∠BAE=∠AED==108°,
∴∠ABE=∠AEB==36°,即∠3=36°,
∴∠4=108°-∠3=72°,
∴∠4=2∠3,
因此B不符合题意;
∵∠4=72°,∠D=108°,
∴∠4+∠D=180°,∴BE∥CD.
∵AF⊥CD,∴AF⊥BE,
因此C不符合题意;
∵AB=AE,AF⊥BE,∴∠1=∠2,
因此A不符合题意;
在Rt△ABG中,∠ABG=36°,∠1=54°,∠AGB=90°,
∴BG≠AB,即BG≠CD,
因此D符合题意.
故选D.
2.C 解析:如图,连结OB、OC,y轴与BC交于点M,
∵正六边形ABCDEF的中心O为原点,
∴∠BOC==60°.
∵OB=OC,∴△BOC是等边三角形,
∴OB=OC=BC=4.
∵OM⊥BC,
∴MC=OC=2,OM=OC=2.
∵点C在第四象限,∴点C的坐标为(2,-2).
故选C.
3.B 解析:如图,由题意,∠AOB=∠COD=108°,∴∠AOD+∠BOC=360°-2×108°=144°,∴的长==4π,∴这个“蘑菇”形图案的周长=4×5+4π=20+4π.故选B.
4.12 解析:如图,连结OA,正六边形的中心角∠AOB=360°÷6=60°,正五边形的中心角∠AOH=360°÷5=72°,∴∠BOH=∠AOH-∠AOB=72°-60°=12°.
5.4 解析:如图,连结AC,过点B作BM⊥AC于点M,
∵六边形ABCDEF是正六边形,
∴∠ABC==120°,AB=BC.
∴∠BAC=∠ACB==30°.
在Rt△ABM中,∠BAM=30°,AB=4 cm,
∴AM=AB=2 cm.
∴AC=2AM=4 cm.
6.4 解析:设AF=x,则AB=x,AH=6-x,∵六边形ABCDEF是正六边形,
∴∠BAF==120°.
∴∠HAF=60°.
∵∠AHF=90°,
∴∠AFH=30°.∴AF=2AH.
∴x=2(6-x).解得x=4.
∴AB=4,即正六边形ABCDEF的边长为4.
7.18 解析:如图,连结CE,正n边形的中心角的度数为,则∠ECF=,∠AEC=.∵∠EGF=30°,∴∠ECF+∠AEC=30°.
∴=30°.解得n=18.
8.解:(1)如图1,首先作直径AD,然后分别以A、D为圆心,OA长为半径画弧,交☉O于点B、F、C、E,连结AB、BC、CD、DE、EF、AF,则六边形ABCDEF即为所求.
图1
(2)四边形BCEF是矩形.
证明如下:如图2,连结OE,
图2
∵六边形ABCDEF是正六边形,
∴AB=AF=DE=DC=FE=BC.
∴.
∴.∴BF=CE.
∴四边形BCEF是平行四边形.
∵六边形ABCDEF是正六边形,
∴∠EDC=∠FED==120°.
∵DE=DC,∴∠DEC=∠DCE=30°.
∴∠CEF=∠DEF-∠CED=90°.
∴四边形BCEF是矩形.
9.(1)证明:连结OF、OA,如图所示.
∵AB=AF=EF,∴.
∴∠ABF=∠AFB=∠EBF=30°.
∵OB=OF,∴∠OBF=∠OFB=30°.
∴∠ABF=∠OFB.∴AB∥OF.
∵FG⊥BA,∴OF⊥FG.
∵OF是☉O的半径,
∴FG是☉O的切线.
(2)解:∵,
∴∠AOF=∠AOB=60°.
∵OA=OF,∴△AOF是等边三角形.
∴∠AOF=∠AOB=∠AFO=∠OAF=60°.
∴AF∥BE,∠AFG=30°.
∵FG=2,∴AF=4,∴OA=4.
∵AF∥BE,∴S△ABF=S△AOF.
∴图中阴影部分的面积=.
圆内接正多边形及相关定义
1.以下图形中,是正多边形的是 ( )
A.平行四边形 B.菱形 C.矩形 D.正方形
2.(易错题)给出下列说法:①各边相等的圆内接多边形是正多边形;②各边相等的圆外切多边形是正多边形;③各角相等的圆内接多边形是正多边形;④各角相等的圆外切多边形是正多边形.其中正确的是 ( )
A.①④ B.②③ C.①③ D.②④
3.内角和与外角和相等的正多边形的对称轴有 ( )
A.4条 B.6条 C.7条 D.8条
圆内接正多边形的相关计算
4.正八边形的一个中心角的度数是 ( )
A.30° B.45° C.60° D.90°
5.如图,正五边形ABCDE内接于☉O,CP与☉O相切于点C,则∠BCP的度数为 ( )
A.120° B.108° C.144° D.162°
6.(跨学科)苯分子的环状结构是由德国化学家凯库勒提出的.随着研究的不断深入,发现苯分子中的6个碳原子与6个氢原子均在同一平面内,且所有碳碳键的键长都相等(如图1),组成了一个完美的六边形(正六边形),图2是其平面示意图,则∠1的度数为 ( )
图1 图2
A.130° B.120° C.110° D.60°
7.(2024重庆渝中区期末)如图,若☉O的半径为3,则其内接正六边形ABCDEF的周长为 .
正多边形的画法
8.用直尺、圆规和量角器作一个正十边形.(写明画法,保留作图痕迹)
1.如图,在正五边形ABCDE中,作AF⊥CD于点F,连结BE与AF交于点G.下列结论,错误的是 ( )
A.∠1=∠2 B.∠4=2∠3
C.AF⊥BE D.BG=CD
2.(2024天津和平区一模)如图,在平面直角坐标系中,正六边形ABCDEF的中心O为原点,顶点A、D在x轴上,若半径是4,则顶点C的坐标为 ( )
A.(2,-) B.(2,-4)
C.(2,-2) D.
3.如图,有公共顶点O的两个边长为5的正五边形(不重叠),以点O为圆心,5为半径作弧,构成一个“蘑菇”形图案(阴影部分),则这个“蘑菇”形图案的周长为 ( )
A.4π B.4π+20
C.10π D.10π+20
4.如图,正六边形ABCDEF和正五边形AHIJK内接于☉O,且有公共顶点A,则∠BOH的度数为 °.
5.(2024上海虹口区二模)如图,已知正六边形螺帽的边长是4 cm,那么与该螺帽匹配的扳手的开口a为 cm.
6.如图,正六边形ABCDEF的顶点A、F分别在正方形BMGH的边BH、GH上.若正方形BMGH的边长为6,则正六边形ABCDEF的边长为 .
7.如图,A、B、C、D、E、F是正n边形的六个连续顶点,AE与CF交于点G,若∠EGF=30°,则n= .
8.如图,已知☉O和☉O上的一点A,请完成下列任务:
(1)用尺规作☉O的内接正六边形ABCDEF;
(2)连结BF、CE,判断四边形BCEF的形状并加以证明.
9.(推理能力)如图,正六边形ABCDEF内接于☉O,BE是☉O的直径,连结BF,延长BA,过F作FG⊥BA,垂足为G.
(1)求证:FG是☉O的切线;
(2)已知FG=2,求图中阴影部分的面积.
【详解答案】
课堂达标
1.D 2.A 3.A 4.B 5.C 6.B
7.18
8.解:如图所示,画法如下:
(1)任意作一个圆,记圆心为O.
(2)作圆心角∠A1OA2==36°.
(3)以A2为圆心,以弦A1A2为半径画弧交☉O于A3,依次作出A4,A5,…,A10.
(4)顺次连结点A1,A2,A3,…,A10,则十边形A1A2…A10为正十边形.
课后提升
1.D 解析:∵五边形ABCDE是正五边形,
∴AB=AE=BC=CD=DE,∠ABC=∠BAE=∠AED==108°,
∴∠ABE=∠AEB==36°,即∠3=36°,
∴∠4=108°-∠3=72°,
∴∠4=2∠3,
因此B不符合题意;
∵∠4=72°,∠D=108°,
∴∠4+∠D=180°,∴BE∥CD.
∵AF⊥CD,∴AF⊥BE,
因此C不符合题意;
∵AB=AE,AF⊥BE,∴∠1=∠2,
因此A不符合题意;
在Rt△ABG中,∠ABG=36°,∠1=54°,∠AGB=90°,
∴BG≠AB,即BG≠CD,
因此D符合题意.
故选D.
2.C 解析:如图,连结OB、OC,y轴与BC交于点M,
∵正六边形ABCDEF的中心O为原点,
∴∠BOC==60°.
∵OB=OC,∴△BOC是等边三角形,
∴OB=OC=BC=4.
∵OM⊥BC,
∴MC=OC=2,OM=OC=2.
∵点C在第四象限,∴点C的坐标为(2,-2).
故选C.
3.B 解析:如图,由题意,∠AOB=∠COD=108°,∴∠AOD+∠BOC=360°-2×108°=144°,∴的长==4π,∴这个“蘑菇”形图案的周长=4×5+4π=20+4π.故选B.
4.12 解析:如图,连结OA,正六边形的中心角∠AOB=360°÷6=60°,正五边形的中心角∠AOH=360°÷5=72°,∴∠BOH=∠AOH-∠AOB=72°-60°=12°.
5.4 解析:如图,连结AC,过点B作BM⊥AC于点M,
∵六边形ABCDEF是正六边形,
∴∠ABC==120°,AB=BC.
∴∠BAC=∠ACB==30°.
在Rt△ABM中,∠BAM=30°,AB=4 cm,
∴AM=AB=2 cm.
∴AC=2AM=4 cm.
6.4 解析:设AF=x,则AB=x,AH=6-x,∵六边形ABCDEF是正六边形,
∴∠BAF==120°.
∴∠HAF=60°.
∵∠AHF=90°,
∴∠AFH=30°.∴AF=2AH.
∴x=2(6-x).解得x=4.
∴AB=4,即正六边形ABCDEF的边长为4.
7.18 解析:如图,连结CE,正n边形的中心角的度数为,则∠ECF=,∠AEC=.∵∠EGF=30°,∴∠ECF+∠AEC=30°.
∴=30°.解得n=18.
8.解:(1)如图1,首先作直径AD,然后分别以A、D为圆心,OA长为半径画弧,交☉O于点B、F、C、E,连结AB、BC、CD、DE、EF、AF,则六边形ABCDEF即为所求.
图1
(2)四边形BCEF是矩形.
证明如下:如图2,连结OE,
图2
∵六边形ABCDEF是正六边形,
∴AB=AF=DE=DC=FE=BC.
∴.
∴.∴BF=CE.
∴四边形BCEF是平行四边形.
∵六边形ABCDEF是正六边形,
∴∠EDC=∠FED==120°.
∵DE=DC,∴∠DEC=∠DCE=30°.
∴∠CEF=∠DEF-∠CED=90°.
∴四边形BCEF是矩形.
9.(1)证明:连结OF、OA,如图所示.
∵AB=AF=EF,∴.
∴∠ABF=∠AFB=∠EBF=30°.
∵OB=OF,∴∠OBF=∠OFB=30°.
∴∠ABF=∠OFB.∴AB∥OF.
∵FG⊥BA,∴OF⊥FG.
∵OF是☉O的半径,
∴FG是☉O的切线.
(2)解:∵,
∴∠AOF=∠AOB=60°.
∵OA=OF,∴△AOF是等边三角形.
∴∠AOF=∠AOB=∠AFO=∠OAF=60°.
∴AF∥BE,∠AFG=30°.
∵FG=2,∴AF=4,∴OA=4.
∵AF∥BE,∴S△ABF=S△AOF.
∴图中阴影部分的面积=.
