期中评估测试卷(含答案) 2024-2025学年数学华东师大版九年级下册
文档属性
| 名称 | 期中评估测试卷(含答案) 2024-2025学年数学华东师大版九年级下册 | 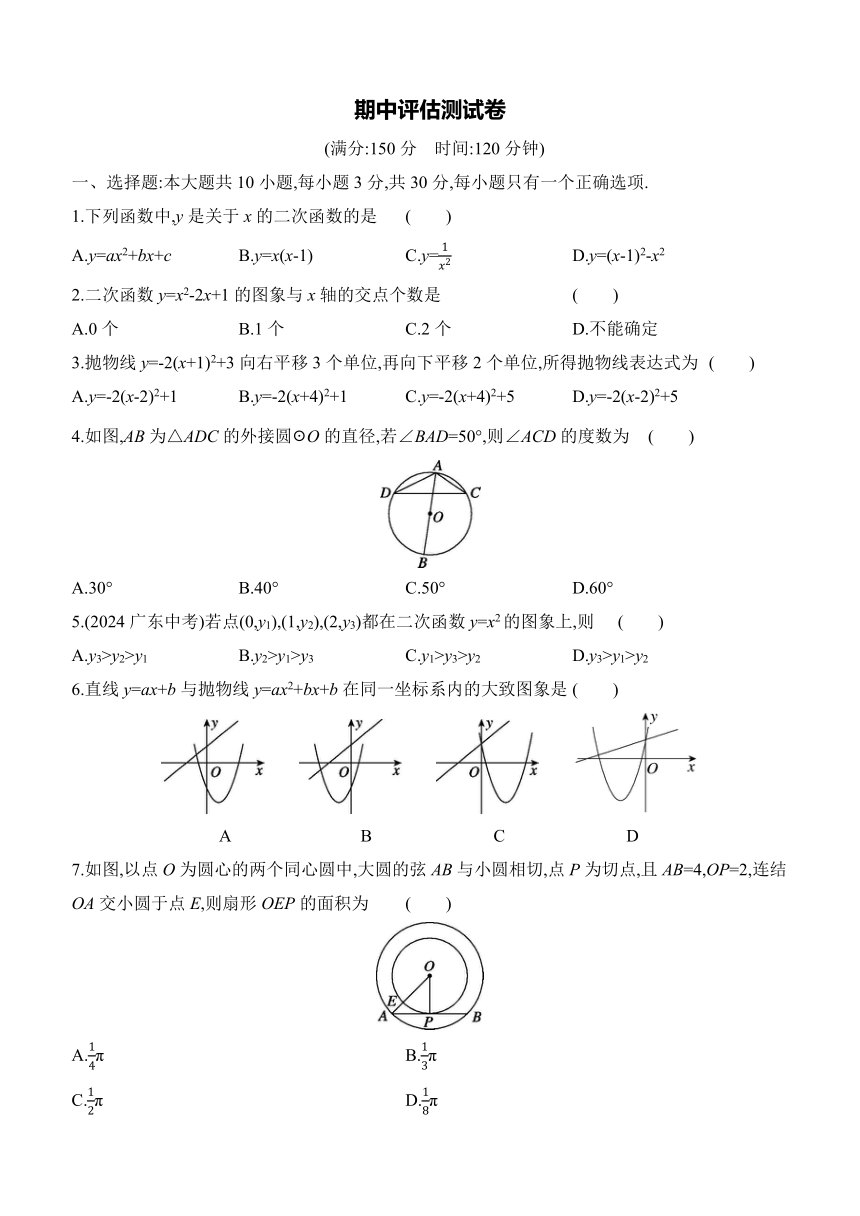 | |
| 格式 | docx | ||
| 文件大小 | 248.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-26 21:53:30 | ||
图片预览




文档简介
期中评估测试卷
(满分:150分 时间:120分钟)
一、选择题:本大题共10小题,每小题3分,共30分,每小题只有一个正确选项.
1.下列函数中,y是关于x的二次函数的是 ( )
A.y=ax2+bx+c B.y=x(x-1) C.y= D.y=(x-1)2-x2
2.二次函数y=x2-2x+1的图象与x轴的交点个数是 ( )
A.0个 B.1个 C.2个 D.不能确定
3.抛物线y=-2(x+1)2+3向右平移3个单位,再向下平移2个单位,所得抛物线表达式为 ( )
A.y=-2(x-2)2+1 B.y=-2(x+4)2+1 C.y=-2(x+4)2+5 D.y=-2(x-2)2+5
4.如图,AB为△ADC的外接圆☉O的直径,若∠BAD=50°,则∠ACD的度数为 ( )
A.30° B.40° C.50° D.60°
5.(2024广东中考)若点(0,y1),(1,y2),(2,y3)都在二次函数y=x2的图象上,则 ( )
A.y3>y2>y1 B.y2>y1>y3 C.y1>y3>y2 D.y3>y1>y2
6.直线y=ax+b与抛物线y=ax2+bx+b在同一坐标系内的大致图象是 ( )
A B C D
7.如图,以点O为圆心的两个同心圆中,大圆的弦AB与小圆相切,点P为切点,且AB=4,OP=2,连结OA交小圆于点E,则扇形OEP的面积为 ( )
A.π B.π
C.π D.π
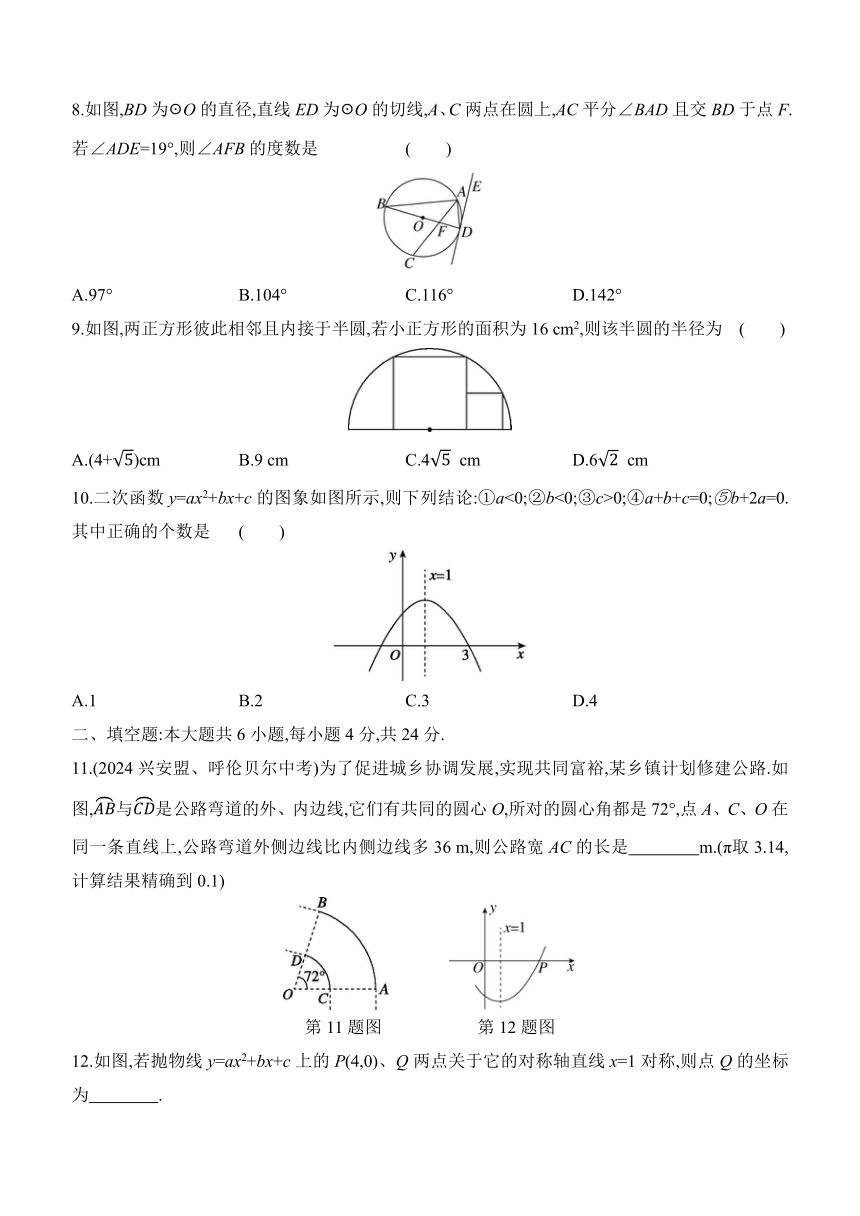
8.如图,BD为☉O的直径,直线ED为☉O的切线,A、C两点在圆上,AC平分∠BAD且交BD于点F.若∠ADE=19°,则∠AFB的度数是 ( )
A.97° B.104° C.116° D.142°
9.如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16 cm2,则该半圆的半径为 ( )
A.(4+)cm B.9 cm C.4 cm D.6 cm
10.二次函数y=ax2+bx+c的图象如图所示,则下列结论:①a<0;②b<0;③c>0;④a+b+c=0;⑤b+2a=0.其中正确的个数是 ( )
A.1 B.2 C.3 D.4
二、填空题:本大题共6小题,每小题4分,共24分.
11.(2024兴安盟、呼伦贝尔中考)为了促进城乡协调发展,实现共同富裕,某乡镇计划修建公路.如图,与是公路弯道的外、内边线,它们有共同的圆心O,所对的圆心角都是72°,点A、C、O在同一条直线上,公路弯道外侧边线比内侧边线多36 m,则公路宽AC的长是 m.(π取3.14,计算结果精确到0.1)
第11题图 第12题图
12.如图,若抛物线y=ax2+bx+c上的P(4,0)、Q两点关于它的对称轴直线x=1对称,则点Q的坐标为 .
13.关于x的分式方程=1的解为非负数,则二次函数y=a2-12a+39的最小值是 .
14.如图,直线y=mx+n与抛物线y=ax2+bx+c交于A(-1,p),B(4,q)两点,则关于x的不等式mx+n> ax2+bx+c的解集是 .
15.(2024资阳中考)如图,在矩形ABCD中,AB=4,AD=2,以点A为圆心,AD长为半径作弧交AB于点E,再以AB为直径作半圆,与交于点F,则图中阴影部分的面积为 .
16.已知同一个圆的内接正六边形与内接正三角形的面积之差为12 cm2,则该圆半径为
cm,内接正六边形的面积为 cm2.
三、解答题:本大题共6小题,共46分.解答时,应写出必要的文字说明、证明过程或演算步骤.
17.(7分)把二次函数y=-x2+x+2化成y=a(x-h)2+k的形式,并指出图象的开口方向、对称轴和顶点坐标.
18.(7分)如图,扇形AOB的圆心角为90°,AB=4,求阴影部分的面积.(结果保留π)
19.(7分)已知抛物线y=x2+2x-3.
(1)求抛物线的顶点坐标;
(2)将该抛物线向右平移m(m>0)个单位,平移后所得新抛物线经过坐标原点,求m的值.
20.(8分)(2024广安期末)如图,四边形ABCD是☉O的内接四边形,△OAB是等边三角形,,求∠ABC的度数.
21.(8分)定义:只有一组对角是直角的四边形叫做损矩形,连结它的两个非直角顶点的线段叫做这个损矩形的直径.
(1)如图,在损矩形ABCD中,∠ABC=∠ADC=90°,则该损矩形的直径是线段 .
(2)①在损矩形ABCD内是否存在点O,使得A、B、C、D四个点都在以O为圆心的同一圆上 如果有,请指出点O的具体位置;如果没有,请说明理由.
②如图,直接写出符合损矩形ABCD的两个结论(不能再添加任何线段或点).
22.(9分)如图,在△ABC中,∠A=45°,以AB为直径的☉O交AC于点D,且AD=DC,CO的延长线交☉O于点E,过点E作弦EF⊥AB,垂足为点G.
(1)求证:BC是☉O的切线;
(2)若AB=2,求EF的长.
四、解答题:本大题共5小题,共50分.解答时,应写出必要的文字说明、证明过程或演算步骤.
23.(9分)如图,抛物线的对称轴是直线x=1,它与x轴交于A、B两点,与y轴交于C点.点A、C的坐标分别是(-1,0),.
(1)求此抛物线对应的函数表达式;
(2)若点P是抛物线上位于x轴上方的一个动点,求△ABP面积的最大值.
24.(9分)一家水果超市以每斤4元的价格购进橘子若干斤,然后以每斤6元的价格出售,每天可售出80斤,通过调查发现,这种橘子每斤的售价每降低0.1元,每天可多售出20斤.
(1)若将橘子每斤的售价降低x元,则每天的销售量是 斤;(用含x的代数式表示)
(2)销售这批橘子要想每天盈利280元,且保证每天至少售出220斤,那么水果店需将每斤的售价降低多少元
(3)当每斤橘子售价为多少元时,才能在一天内获得最大利润 最大利润是多少
25.(10分)如图,AN是☉M的直径,NB∥x轴,AB与☉M的另一交点为点C.
(1)若点A(0,6),N(0,2),∠ABN=30°,求点B的坐标;
(2)若D为线段NB的中点,求证:CD是☉M的切线.
26.(10分)如图,△ABC内接于☉O,∠BAC的平分线AF交☉O于点G,过点G作DE∥BC分别交AB、AC的延长线于点D、E.
(1)求证:DE是☉O的切线;
(2)已知AG=6,,点I为△ABC的内心,求GI的长.
27.(12分)(2024甘孜州中考)【定义与性质】
如图,记二次函数y=a(x-b)2+c和y=-a(x-p)2+q(a≠0)的图象分别为抛物线C和C1.
定义:若抛物线C1的顶点Q(p,q)在抛物线C上,则称C1是C的伴随抛物线.
性质:①一条抛物线有无数条伴随抛物线;
②若C1是C的伴随抛物线,则C也是C1的伴随抛物线,即C的顶点P(b,c)在C1上.
【理解与运用】
(1)若二次函数y=-(x-2)2+m和y=-(x-n)2+的图象都是抛物线y=x2的伴随抛物线,则m= , n= ;
【思考与探究】
(2)设函数y=x2-2kx+4k+5的图象为抛物线C2.
①若函数y=-x2+dx+e的图象为抛物线C0,且C2始终是C0的伴随抛物线,求d、e的值;
②若抛物线C2与x轴有两个不同的交点(x1,0),(x2,0)(x1
备用图
【详解答案】
1.B 2.B 3.A 4.B 5.A
6.D 解析:由已知得直线y=ax+b和抛物线y=ax2+bx+b过点(0,b),排除A,B;对于C,D,由一次函数的图象得a>0,b>0,此时二次函数的对称轴应在y轴左侧,排除C.故选D.
7.C 解析:∵大圆的弦AB与小圆相切,
∴OP垂直平分弦AB,
∴AP=AB=2.
又∵OP=2.
∴△OAP为等腰直角三角形.
∴∠AOP=45°.
∴S扇形OEP=π.故选C.
8.C 解析:∵BD为☉O的直径,
∴∠BAD=90°.
又∵AC平分∠BAD,
∴∠BAF=∠DAF=45°.
∵直线ED为☉O的切线,
∴∠BDE=90°.
∵∠ADE=19°,
∴∠BDA=∠BDE-∠ADE=90°-19°=71°.
∴∠AFB=∠BDA+∠DAF=71°+45°=116°.故选C.
9.C 解析:如图,连结OA、OB、OE,
∵四边形ABCD是正方形,
∴AD=BC=DC,
∠ADO=∠BCO=90°.
在Rt△ADO和Rt△BCO中,
∵
∴Rt△ADO≌Rt△BCO(H.L.),
∴OD=OC.
设AD=a cm,则OD=OC=DC=AD=a cm,
在△AOD中,由勾股定理得OA=OB=OE=a cm,
∵小正方形EFCG的面积为16 cm2,
∴EF=FC=4 cm,
在△OFE中,由勾股定理,得
=42+,
解得a=-4(舍去)或a=8,
∴a=4 cm.
故选C.
10.C 解析:∵二次函数的图象的开口向下,
∴a<0.
∵二次函数的图象与y轴的交点在y轴的正半轴上,
∴c>0.
∴①③正确;
∵对称轴为直线x=-=1,
∴2a=-b,
∴2a+b=0.
∴a、b异号,即b>0.
∴②错误,⑤正确;
∵当x=1时,y=a+b+c>0,
∴④错误.
综上可知①③⑤正确.
故选C.
11.28.7 解析:由题意得=36,
∴OA-OC=≈28.7(m),
∴AC=OA-OC≈28.7 m.
12.(-2,0) 解析:设点Q(t,0),∵二次函数图象的对称轴是直线x=1,且P(4,0),∴=1,∴t=-2,∴Q(-2,0).
13.4 解析:解关于x的方程=1,得x=5-a,
∵关于x的分式方程=1的解为非负数,
∴x=5-a≥0,且5-a≠2,
解得a≤5且a≠3.
∵二次函数y=a2-12a+39=(a-6)2+3,
∴当a<6时,y随a的增大而减小.
∵a≤5且a≠3,
∴当a=5时,二次函数y=a2-12a+39的最小值为4.
14.x<-1或x>4 解析:观察函数图象可知:当x<-1或x>4时,直线y=mx+n在抛物线y=ax2+bx+c的上方,∴不等式mx+n>ax2+bx+c的解集为x<-1或x>4.
15.π 解析:如图,连结AF、EF.
由题意易知△AEF是等边三角形,
S阴影=S半圆-S扇形EAF-S弓形AF
=2π--×2××2
=π.
16.4 24 解析:设该圆半径为r cm,
如图1,∵△ABC为等边三角形,
OC=r cm,
∴OD=OC=r cm,BC=2CD=r cm,
∴内接正三角形的面积=3×r×r=r2(cm2).
图1 图2
如图2,∵∠AOB=60°,OA=OB,
∴△AOB是等边三角形,∴OA=AB=r cm,
∴AD=OA=r cm,
∴OD=r cm,
∴圆的内接正六边形的面积=6××r×r=r2(cm2).
∵一个圆的内接正六边形与内接正三角形的面积之差为12 cm2,
∴r2-r2=12,
∴r=4(负值舍去),
∴内接正六边形的面积为24 cm2.
17.解:y=-x2+x+2=-(x2-x)+2=-.
图象开口向下,对称轴为直线x=,顶点坐标为.
18.解:∵∠AOB=90°,OA=OB,
∴△AOB为等腰直角三角形.
∵AB=4,
∴2OA2=AB2=(4)2=32.
∴OA=OB=4.
∴S阴影部分=S扇形AOB-S△AOB=×4×4=4π-8.
19.解:(1)∵y=x2+2x-3=(x+1)2-4,
∴抛物线的顶点坐标为(-1,-4).
(2)该抛物线向右平移m(m>0)个单位,得到的新抛物线对应的函数表达式为y=(x+1-m)2-4,
∵新抛物线经过原点,
∴0=(0+1-m)2-4,
解得m=3或m=-1(舍去),
∴m=3,
故m的值为3.
20.解:∵△OAB是等边三角形,
∴∠AOB=60°.
∴∠ADB=∠AOB=30°.
∵,
∴∠ADB=∠BDC=30°.
∴∠ADC=30°+30°=60°.
∵四边形ABCD是☉O的内接四边形,
∴∠ABC=180°-∠ADC=120°.
21.解:(1)AC
(2)①在损矩形ABCD内存在点O,
使得A、B、C、D四个点都在以O为圆心的同一个圆上,
O是线段AC的中点.
②四边形ABCD是圆内接四边形;
∠ADB=∠ACB.(答案不唯一)
22.(1)证明:如图,连结BD,
∵AB为☉O的直径,
∴∠ADB=90°.
∴BD⊥AC.
∵AD=CD,
∴AB=BC.
∴∠A=∠ACB=45°.
∴∠ABC=90°.
∵AB是☉O的直径,
∴BC是☉O的切线.
(2)解:∵AB=2,
∴BO=1.
∵AB=BC=2,
∴CO=.
∵EF⊥AB,BC⊥AB,
∴EF∥BC.
∴△EGO∽△CBO.
∴.
∴.
∴EG=.
∴EF=2EG=.
23.解:(1)设所求的函数表达式为y=ax2+bx+c(a≠0),
则解得
∴所求函数表达式为y=-x2+x+.
(2)当点P是抛物线的顶点时,△ABP面积最大.
由(1)知,B(3,0),当x=1时,y=2,
∴顶点坐标是(1,2).
∴△ABP面积的最大值为×|AB|×2=×4×2=4.
24.解:(1)(80+200x)
(2)根据题意,得
(6-4-x)(80+200x)=280,
解得x1=,x2=1,
当x=时,销售量是80+200×=200<220;
当x=1时,销售量是80+200=280(斤).
∵每天至少售出220斤,
∴x=1.
答:水果店需将每斤的售价降低1元.
(3)设每斤的售价降低m元,每天获利为w元,根据题意,得
w=(6-4-m)(80+200m)=-200m2+320m+160=-200+288,
当m=时,w有最大值,最大值为288元,
售价为6-(元).
答:当每斤橘子售价为元时,才能在一天内获得最大利润,最大利润是288元.
25.(1)解:∵A(0,6),N(0,2),
∴AN=4.
∵∠ABN=30°,∠ANB=90°,
∴AB=2AN=8.
∴NB==4.
∴B(4,2).
(2)证明:如图,连结MC、NC.
∵AN是☉M的直径,
∴∠ACN=90°.
∴∠NCB=90°.
在Rt△NCB中,D为NB的中点,
∴CD=NB=ND,
∴∠CND=∠NCD.
∵MC=MN,
∴∠MCN=∠MNC.
∵∠MNC+∠CND=90°,
∴∠MCN+∠NCD=90°.
即MC⊥CD.
∵MC是☉O的半径,
∴CD是☉M的切线.
26.(1)证明:如图,连结OG,
∵∠BAC的平分线AF交☉O于点G,
∴∠BAG=∠CAG.
∴.
∴OG⊥BC.
∵DE∥BC,
∴OG⊥DE.
∵OG是☉O的半径,
∴DE是☉O的切线.
(2)解:如图,连结BI、BG,
∵点I为△ABC的内心,
∴BI平分∠ABC,AG平分∠BAC,
∴∠BAI=∠CAI,∠ABI=∠CBI.
∵∠BIG=∠BAI+∠ABI,∠GBI=∠GBC+∠CBI,∠GBC=∠GAC,
∴∠BAI=∠GBC.
∴∠BIG=∠GBI.
∴BG=IG.
∵BC∥DE,
∴△ACF∽△AEG.
∴.
∵AG=6,
∴AF=4.
∴FG=2.
∵∠BGF=∠AGB,∠GBF=∠BAG,
∴△BGF∽△AGB.
∴.
∴.
∴BG=2(负值舍去),
∴GI的长为2.
27.解:(1)2 ±1
(2)①∵y=x2-2kx+4k+5=(x-k)2-k2+4k+5,
∴抛物线C2的顶点为(k,-k2+4k+5).
又∵C2始终是C0的伴随抛物线,
∴可令k=0,顶点为(0,5);k=1,顶点为(1,8),
∴解得
∴d=4,e=5.
②2解析:由①,得函数y=-x2+4x+5的图象为抛物线C0,且C2始终是C0的伴随抛物线,
∴C2的顶点(k,-k2+4k+5)在y=
-x2+4x+5=-(x-2)2+9图象上滑动,C0的顶点为(2,9),
当-x2+4x+5=0时,解得x=-1或x=5,
∴抛物线C0与x轴交于(-1,0),(5,0)两个点,
∵C2与x轴有两个不同的交点(x1,0),(x2,0),
∴当C2的顶点在(-1,0)下方时,抛物线C2有两个交点,x1<-1;
∵若C1是C的伴随抛物线,则C也是C1的伴随抛物线,即C的顶点P(b,c)在C1上,
∴(2,9)在C2上,
当顶点在(5,0)下方时,2综上,2
(满分:150分 时间:120分钟)
一、选择题:本大题共10小题,每小题3分,共30分,每小题只有一个正确选项.
1.下列函数中,y是关于x的二次函数的是 ( )
A.y=ax2+bx+c B.y=x(x-1) C.y= D.y=(x-1)2-x2
2.二次函数y=x2-2x+1的图象与x轴的交点个数是 ( )
A.0个 B.1个 C.2个 D.不能确定
3.抛物线y=-2(x+1)2+3向右平移3个单位,再向下平移2个单位,所得抛物线表达式为 ( )
A.y=-2(x-2)2+1 B.y=-2(x+4)2+1 C.y=-2(x+4)2+5 D.y=-2(x-2)2+5
4.如图,AB为△ADC的外接圆☉O的直径,若∠BAD=50°,则∠ACD的度数为 ( )
A.30° B.40° C.50° D.60°
5.(2024广东中考)若点(0,y1),(1,y2),(2,y3)都在二次函数y=x2的图象上,则 ( )
A.y3>y2>y1 B.y2>y1>y3 C.y1>y3>y2 D.y3>y1>y2
6.直线y=ax+b与抛物线y=ax2+bx+b在同一坐标系内的大致图象是 ( )
A B C D
7.如图,以点O为圆心的两个同心圆中,大圆的弦AB与小圆相切,点P为切点,且AB=4,OP=2,连结OA交小圆于点E,则扇形OEP的面积为 ( )
A.π B.π
C.π D.π
8.如图,BD为☉O的直径,直线ED为☉O的切线,A、C两点在圆上,AC平分∠BAD且交BD于点F.若∠ADE=19°,则∠AFB的度数是 ( )
A.97° B.104° C.116° D.142°
9.如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16 cm2,则该半圆的半径为 ( )
A.(4+)cm B.9 cm C.4 cm D.6 cm
10.二次函数y=ax2+bx+c的图象如图所示,则下列结论:①a<0;②b<0;③c>0;④a+b+c=0;⑤b+2a=0.其中正确的个数是 ( )
A.1 B.2 C.3 D.4
二、填空题:本大题共6小题,每小题4分,共24分.
11.(2024兴安盟、呼伦贝尔中考)为了促进城乡协调发展,实现共同富裕,某乡镇计划修建公路.如图,与是公路弯道的外、内边线,它们有共同的圆心O,所对的圆心角都是72°,点A、C、O在同一条直线上,公路弯道外侧边线比内侧边线多36 m,则公路宽AC的长是 m.(π取3.14,计算结果精确到0.1)
第11题图 第12题图
12.如图,若抛物线y=ax2+bx+c上的P(4,0)、Q两点关于它的对称轴直线x=1对称,则点Q的坐标为 .
13.关于x的分式方程=1的解为非负数,则二次函数y=a2-12a+39的最小值是 .
14.如图,直线y=mx+n与抛物线y=ax2+bx+c交于A(-1,p),B(4,q)两点,则关于x的不等式mx+n> ax2+bx+c的解集是 .
15.(2024资阳中考)如图,在矩形ABCD中,AB=4,AD=2,以点A为圆心,AD长为半径作弧交AB于点E,再以AB为直径作半圆,与交于点F,则图中阴影部分的面积为 .
16.已知同一个圆的内接正六边形与内接正三角形的面积之差为12 cm2,则该圆半径为
cm,内接正六边形的面积为 cm2.
三、解答题:本大题共6小题,共46分.解答时,应写出必要的文字说明、证明过程或演算步骤.
17.(7分)把二次函数y=-x2+x+2化成y=a(x-h)2+k的形式,并指出图象的开口方向、对称轴和顶点坐标.
18.(7分)如图,扇形AOB的圆心角为90°,AB=4,求阴影部分的面积.(结果保留π)
19.(7分)已知抛物线y=x2+2x-3.
(1)求抛物线的顶点坐标;
(2)将该抛物线向右平移m(m>0)个单位,平移后所得新抛物线经过坐标原点,求m的值.
20.(8分)(2024广安期末)如图,四边形ABCD是☉O的内接四边形,△OAB是等边三角形,,求∠ABC的度数.
21.(8分)定义:只有一组对角是直角的四边形叫做损矩形,连结它的两个非直角顶点的线段叫做这个损矩形的直径.
(1)如图,在损矩形ABCD中,∠ABC=∠ADC=90°,则该损矩形的直径是线段 .
(2)①在损矩形ABCD内是否存在点O,使得A、B、C、D四个点都在以O为圆心的同一圆上 如果有,请指出点O的具体位置;如果没有,请说明理由.
②如图,直接写出符合损矩形ABCD的两个结论(不能再添加任何线段或点).
22.(9分)如图,在△ABC中,∠A=45°,以AB为直径的☉O交AC于点D,且AD=DC,CO的延长线交☉O于点E,过点E作弦EF⊥AB,垂足为点G.
(1)求证:BC是☉O的切线;
(2)若AB=2,求EF的长.
四、解答题:本大题共5小题,共50分.解答时,应写出必要的文字说明、证明过程或演算步骤.
23.(9分)如图,抛物线的对称轴是直线x=1,它与x轴交于A、B两点,与y轴交于C点.点A、C的坐标分别是(-1,0),.
(1)求此抛物线对应的函数表达式;
(2)若点P是抛物线上位于x轴上方的一个动点,求△ABP面积的最大值.
24.(9分)一家水果超市以每斤4元的价格购进橘子若干斤,然后以每斤6元的价格出售,每天可售出80斤,通过调查发现,这种橘子每斤的售价每降低0.1元,每天可多售出20斤.
(1)若将橘子每斤的售价降低x元,则每天的销售量是 斤;(用含x的代数式表示)
(2)销售这批橘子要想每天盈利280元,且保证每天至少售出220斤,那么水果店需将每斤的售价降低多少元
(3)当每斤橘子售价为多少元时,才能在一天内获得最大利润 最大利润是多少
25.(10分)如图,AN是☉M的直径,NB∥x轴,AB与☉M的另一交点为点C.
(1)若点A(0,6),N(0,2),∠ABN=30°,求点B的坐标;
(2)若D为线段NB的中点,求证:CD是☉M的切线.
26.(10分)如图,△ABC内接于☉O,∠BAC的平分线AF交☉O于点G,过点G作DE∥BC分别交AB、AC的延长线于点D、E.
(1)求证:DE是☉O的切线;
(2)已知AG=6,,点I为△ABC的内心,求GI的长.
27.(12分)(2024甘孜州中考)【定义与性质】
如图,记二次函数y=a(x-b)2+c和y=-a(x-p)2+q(a≠0)的图象分别为抛物线C和C1.
定义:若抛物线C1的顶点Q(p,q)在抛物线C上,则称C1是C的伴随抛物线.
性质:①一条抛物线有无数条伴随抛物线;
②若C1是C的伴随抛物线,则C也是C1的伴随抛物线,即C的顶点P(b,c)在C1上.
【理解与运用】
(1)若二次函数y=-(x-2)2+m和y=-(x-n)2+的图象都是抛物线y=x2的伴随抛物线,则m= , n= ;
【思考与探究】
(2)设函数y=x2-2kx+4k+5的图象为抛物线C2.
①若函数y=-x2+dx+e的图象为抛物线C0,且C2始终是C0的伴随抛物线,求d、e的值;
②若抛物线C2与x轴有两个不同的交点(x1,0),(x2,0)(x1
备用图
【详解答案】
1.B 2.B 3.A 4.B 5.A
6.D 解析:由已知得直线y=ax+b和抛物线y=ax2+bx+b过点(0,b),排除A,B;对于C,D,由一次函数的图象得a>0,b>0,此时二次函数的对称轴应在y轴左侧,排除C.故选D.
7.C 解析:∵大圆的弦AB与小圆相切,
∴OP垂直平分弦AB,
∴AP=AB=2.
又∵OP=2.
∴△OAP为等腰直角三角形.
∴∠AOP=45°.
∴S扇形OEP=π.故选C.
8.C 解析:∵BD为☉O的直径,
∴∠BAD=90°.
又∵AC平分∠BAD,
∴∠BAF=∠DAF=45°.
∵直线ED为☉O的切线,
∴∠BDE=90°.
∵∠ADE=19°,
∴∠BDA=∠BDE-∠ADE=90°-19°=71°.
∴∠AFB=∠BDA+∠DAF=71°+45°=116°.故选C.
9.C 解析:如图,连结OA、OB、OE,
∵四边形ABCD是正方形,
∴AD=BC=DC,
∠ADO=∠BCO=90°.
在Rt△ADO和Rt△BCO中,
∵
∴Rt△ADO≌Rt△BCO(H.L.),
∴OD=OC.
设AD=a cm,则OD=OC=DC=AD=a cm,
在△AOD中,由勾股定理得OA=OB=OE=a cm,
∵小正方形EFCG的面积为16 cm2,
∴EF=FC=4 cm,
在△OFE中,由勾股定理,得
=42+,
解得a=-4(舍去)或a=8,
∴a=4 cm.
故选C.
10.C 解析:∵二次函数的图象的开口向下,
∴a<0.
∵二次函数的图象与y轴的交点在y轴的正半轴上,
∴c>0.
∴①③正确;
∵对称轴为直线x=-=1,
∴2a=-b,
∴2a+b=0.
∴a、b异号,即b>0.
∴②错误,⑤正确;
∵当x=1时,y=a+b+c>0,
∴④错误.
综上可知①③⑤正确.
故选C.
11.28.7 解析:由题意得=36,
∴OA-OC=≈28.7(m),
∴AC=OA-OC≈28.7 m.
12.(-2,0) 解析:设点Q(t,0),∵二次函数图象的对称轴是直线x=1,且P(4,0),∴=1,∴t=-2,∴Q(-2,0).
13.4 解析:解关于x的方程=1,得x=5-a,
∵关于x的分式方程=1的解为非负数,
∴x=5-a≥0,且5-a≠2,
解得a≤5且a≠3.
∵二次函数y=a2-12a+39=(a-6)2+3,
∴当a<6时,y随a的增大而减小.
∵a≤5且a≠3,
∴当a=5时,二次函数y=a2-12a+39的最小值为4.
14.x<-1或x>4 解析:观察函数图象可知:当x<-1或x>4时,直线y=mx+n在抛物线y=ax2+bx+c的上方,∴不等式mx+n>ax2+bx+c的解集为x<-1或x>4.
15.π 解析:如图,连结AF、EF.
由题意易知△AEF是等边三角形,
S阴影=S半圆-S扇形EAF-S弓形AF
=2π--×2××2
=π.
16.4 24 解析:设该圆半径为r cm,
如图1,∵△ABC为等边三角形,
OC=r cm,
∴OD=OC=r cm,BC=2CD=r cm,
∴内接正三角形的面积=3×r×r=r2(cm2).
图1 图2
如图2,∵∠AOB=60°,OA=OB,
∴△AOB是等边三角形,∴OA=AB=r cm,
∴AD=OA=r cm,
∴OD=r cm,
∴圆的内接正六边形的面积=6××r×r=r2(cm2).
∵一个圆的内接正六边形与内接正三角形的面积之差为12 cm2,
∴r2-r2=12,
∴r=4(负值舍去),
∴内接正六边形的面积为24 cm2.
17.解:y=-x2+x+2=-(x2-x)+2=-.
图象开口向下,对称轴为直线x=,顶点坐标为.
18.解:∵∠AOB=90°,OA=OB,
∴△AOB为等腰直角三角形.
∵AB=4,
∴2OA2=AB2=(4)2=32.
∴OA=OB=4.
∴S阴影部分=S扇形AOB-S△AOB=×4×4=4π-8.
19.解:(1)∵y=x2+2x-3=(x+1)2-4,
∴抛物线的顶点坐标为(-1,-4).
(2)该抛物线向右平移m(m>0)个单位,得到的新抛物线对应的函数表达式为y=(x+1-m)2-4,
∵新抛物线经过原点,
∴0=(0+1-m)2-4,
解得m=3或m=-1(舍去),
∴m=3,
故m的值为3.
20.解:∵△OAB是等边三角形,
∴∠AOB=60°.
∴∠ADB=∠AOB=30°.
∵,
∴∠ADB=∠BDC=30°.
∴∠ADC=30°+30°=60°.
∵四边形ABCD是☉O的内接四边形,
∴∠ABC=180°-∠ADC=120°.
21.解:(1)AC
(2)①在损矩形ABCD内存在点O,
使得A、B、C、D四个点都在以O为圆心的同一个圆上,
O是线段AC的中点.
②四边形ABCD是圆内接四边形;
∠ADB=∠ACB.(答案不唯一)
22.(1)证明:如图,连结BD,
∵AB为☉O的直径,
∴∠ADB=90°.
∴BD⊥AC.
∵AD=CD,
∴AB=BC.
∴∠A=∠ACB=45°.
∴∠ABC=90°.
∵AB是☉O的直径,
∴BC是☉O的切线.
(2)解:∵AB=2,
∴BO=1.
∵AB=BC=2,
∴CO=.
∵EF⊥AB,BC⊥AB,
∴EF∥BC.
∴△EGO∽△CBO.
∴.
∴.
∴EG=.
∴EF=2EG=.
23.解:(1)设所求的函数表达式为y=ax2+bx+c(a≠0),
则解得
∴所求函数表达式为y=-x2+x+.
(2)当点P是抛物线的顶点时,△ABP面积最大.
由(1)知,B(3,0),当x=1时,y=2,
∴顶点坐标是(1,2).
∴△ABP面积的最大值为×|AB|×2=×4×2=4.
24.解:(1)(80+200x)
(2)根据题意,得
(6-4-x)(80+200x)=280,
解得x1=,x2=1,
当x=时,销售量是80+200×=200<220;
当x=1时,销售量是80+200=280(斤).
∵每天至少售出220斤,
∴x=1.
答:水果店需将每斤的售价降低1元.
(3)设每斤的售价降低m元,每天获利为w元,根据题意,得
w=(6-4-m)(80+200m)=-200m2+320m+160=-200+288,
当m=时,w有最大值,最大值为288元,
售价为6-(元).
答:当每斤橘子售价为元时,才能在一天内获得最大利润,最大利润是288元.
25.(1)解:∵A(0,6),N(0,2),
∴AN=4.
∵∠ABN=30°,∠ANB=90°,
∴AB=2AN=8.
∴NB==4.
∴B(4,2).
(2)证明:如图,连结MC、NC.
∵AN是☉M的直径,
∴∠ACN=90°.
∴∠NCB=90°.
在Rt△NCB中,D为NB的中点,
∴CD=NB=ND,
∴∠CND=∠NCD.
∵MC=MN,
∴∠MCN=∠MNC.
∵∠MNC+∠CND=90°,
∴∠MCN+∠NCD=90°.
即MC⊥CD.
∵MC是☉O的半径,
∴CD是☉M的切线.
26.(1)证明:如图,连结OG,
∵∠BAC的平分线AF交☉O于点G,
∴∠BAG=∠CAG.
∴.
∴OG⊥BC.
∵DE∥BC,
∴OG⊥DE.
∵OG是☉O的半径,
∴DE是☉O的切线.
(2)解:如图,连结BI、BG,
∵点I为△ABC的内心,
∴BI平分∠ABC,AG平分∠BAC,
∴∠BAI=∠CAI,∠ABI=∠CBI.
∵∠BIG=∠BAI+∠ABI,∠GBI=∠GBC+∠CBI,∠GBC=∠GAC,
∴∠BAI=∠GBC.
∴∠BIG=∠GBI.
∴BG=IG.
∵BC∥DE,
∴△ACF∽△AEG.
∴.
∵AG=6,
∴AF=4.
∴FG=2.
∵∠BGF=∠AGB,∠GBF=∠BAG,
∴△BGF∽△AGB.
∴.
∴.
∴BG=2(负值舍去),
∴GI的长为2.
27.解:(1)2 ±1
(2)①∵y=x2-2kx+4k+5=(x-k)2-k2+4k+5,
∴抛物线C2的顶点为(k,-k2+4k+5).
又∵C2始终是C0的伴随抛物线,
∴可令k=0,顶点为(0,5);k=1,顶点为(1,8),
∴解得
∴d=4,e=5.
②2
∴C2的顶点(k,-k2+4k+5)在y=
-x2+4x+5=-(x-2)2+9图象上滑动,C0的顶点为(2,9),
当-x2+4x+5=0时,解得x=-1或x=5,
∴抛物线C0与x轴交于(-1,0),(5,0)两个点,
∵C2与x轴有两个不同的交点(x1,0),(x2,0),
∴当C2的顶点在(-1,0)下方时,抛物线C2有两个交点,x1<-1;
∵若C1是C的伴随抛物线,则C也是C1的伴随抛物线,即C的顶点P(b,c)在C1上,
∴(2,9)在C2上,
当顶点在(5,0)下方时,2
同课章节目录
