29.3切线的性质和判定 课时作业(含详解) 2024-2025学年数学冀教版九年级下册
文档属性
| 名称 | 29.3切线的性质和判定 课时作业(含详解) 2024-2025学年数学冀教版九年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 382.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-26 00:00:00 | ||
图片预览





文档简介
29.3切线的性质和判定
切线的性质
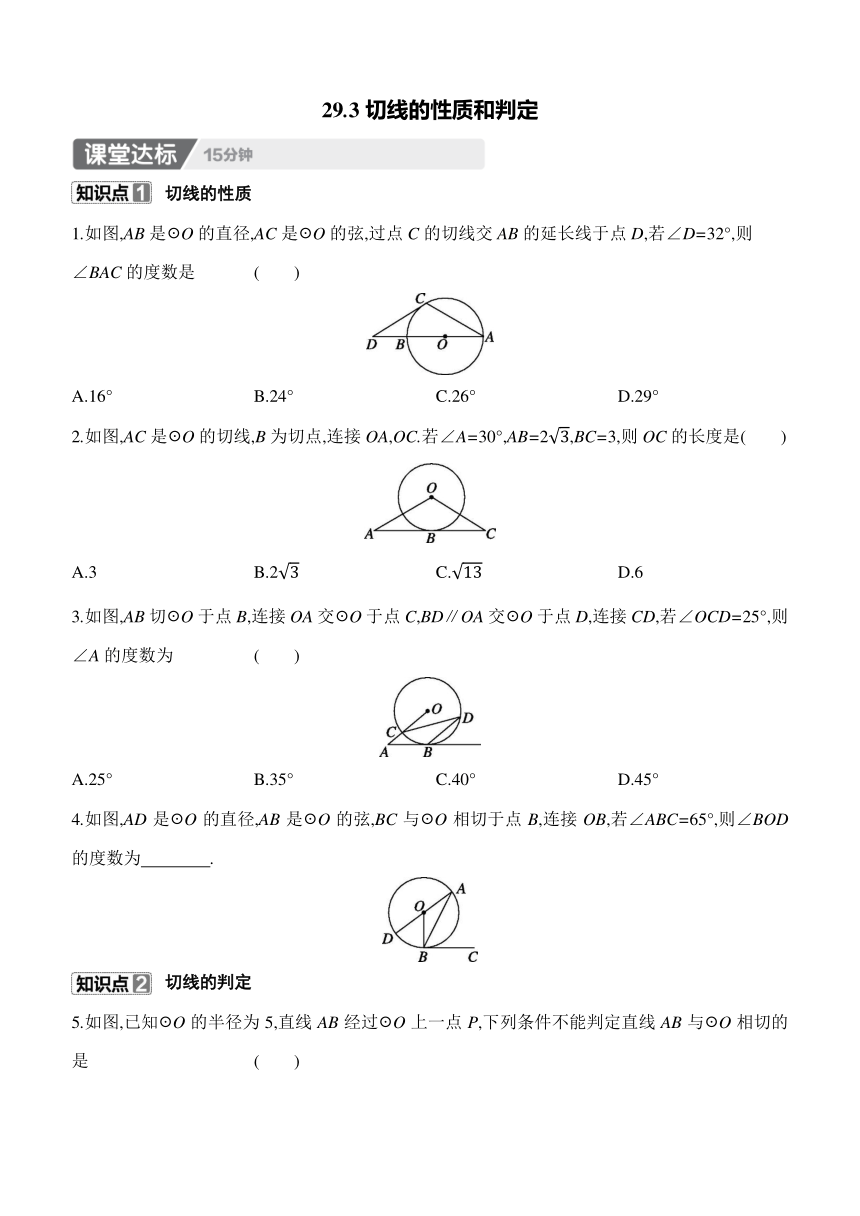
1.如图,AB是☉O的直径,AC是☉O的弦,过点C的切线交AB的延长线于点D,若∠D=32°,则
∠BAC的度数是 ( )
A.16° B.24° C.26° D.29°
2.如图,AC是☉O的切线,B为切点,连接OA,OC.若∠A=30°,AB=2,BC=3,则OC的长度是( )
A.3 B.2 C. D.6
3.如图,AB切☉O于点B,连接OA交☉O于点C,BD∥OA交☉O于点D,连接CD,若∠OCD=25°,则∠A的度数为 ( )
A.25° B.35° C.40° D.45°
4.如图,AD是☉O的直径,AB是☉O的弦,BC与☉O相切于点B,连接OB,若∠ABC=65°,则∠BOD的度数为 .
切线的判定
5.如图,已知☉O的半径为5,直线AB经过☉O上一点P,下列条件不能判定直线AB与☉O相切的是 ( )
A.OP=5
B.∠APO=∠BPO
C.点O到直线AB的距离是5
D.OP⊥AB
6.如图,点B在☉A 上,点C在☉A外,下列条件不能判定 BC是☉A的切线的是( )
A.∠A=50°,∠C=40°
B.∠B-∠C=∠A
C.AB2 +BC2 =AC2
D.☉A与AC的交点是AC的中点
7.如图,在Rt△ABC中,∠ACB=90°,以AC为直径的☉O与AB边交于点D,EB=EC.
(1)求证:DE是☉O的切线.
(2)若以点O,D,E,C为顶点的四边形是正方形,试判断△ABC的形状,并说明理由.
1.有一道题目:“如图,AB是☉O的直径,要使直线AP是☉O的切线,需添加的条件是 (写一个条件即可).”下面是三位同学写的答案,则下列判断正确的是 ( )
甲:∠BAP=90°;乙:∠BAC=∠PAC;
丙:∠BAC=∠P.
A.只有甲同学的答案正确 B.只有乙同学的答案正确
C.只有甲、丙同学的答案正确 D.三位同学的答案都正确
2.如图,AB是☉O的直径,CD是☉O的切线,D为切点,AC⊥CD,垂足为C,连接BD.若AB=8,且
∠B=30°,则CD的长为 ( )
A.2 B.2 C.4 D.4
3.如图,在平面直角坐标系中,点A,B在函数y=(k>0,x>0)的图像上,分别以点A,B为圆心,1为半径作圆,当☉A与x轴相切、☉B与y轴相切时,连接AB,AB=3,则k的值为 ( )
A.3 B.3 C.4 D.6
4.如图,AB是☉O的直径,P是AB延长线上的一点,PC是☉O的切线,C为切点.若PA=64,tan P=,则PC= .
5.如图,在Rt△ABC中,∠ACB=90°,点O在边AC上,以点O为圆心,OC为半径的半圆与斜边AB相切于点D,交OA于点E,连接OB.
(1)求证:BD=BC.
(2)已知OC=1,∠A=30°,求AB的长.
6.如图,已知AB是☉O的直径,直线DC是☉O的切线,切点为C,AE⊥DC,垂足为E,连接AC.
(1)求证:AC平分∠BAE.
(2)若AC=5,tan∠ACE=,求☉O的半径.
7.(运算能力)如图,等腰三角形ABC内接于☉O,AB=AC,BD是边AC上的中线,过点C作AB的平行线交BD的延长线于点E,BE交☉O于点F,连接AE,FC.
(1)求证:AE为☉O的切线.
(2)若☉O的半径为5,BC=6,求FC的长.
【详解答案】
课堂达标
1.D 解析:如图,连接OC.
∵CD与☉O相切于点C,∴CD⊥OC.∴∠OCD=90°.∵∠D=32°,∴∠DOC=90°-∠D=90°-32°=58°.
∴∠BAC=∠DOC=×58°=29°.故选D.
2.C 解析:如图,连接OB.∵AC是☉O的切线,B为切点,∴OB⊥AC.∵∠A=30°,AB=2,∴在Rt△OAB中,OB=AB·tan A=2=2.∵BC=3,∴在Rt△OBC中,OC==.故选C.
3.C 解析:如图,连接OB.
∵AB切☉O于点B,∴∠ABO=90°.∵BD∥OA, ∠OCD=25°,∴∠CDB=25°.∴∠BOC=2∠BDC=50°.∴∠A=40°.故选C.
4.50° 解析:∵BC与☉O相切于点B,∴∠OBC=90°.∵∠ABC=65°,∴∠OBA=90°-65°=25°.
∵OB=OA,∴∠A=∠OBA=25°.∴∠BOD=2×25°=50°.
5.A 解析:A.OP=5,不能判定直线AB与☉O相切,符合题意;B.由∠APO=∠BPO,得到OP⊥AB,且点P在☉O上,能判定直线AB与☉O相切,不符合题意;C.点O到直线AB的距离是5,等于半径,能判定直线AB与☉O相切,不符合题意;D.OP⊥AB且点P在☉O上,能判定直线AB与☉O相切,不符合题意.故选A.
6.D 解析:∵∠A=50°,∠C=40°,∴∠B=90°.∴BC为☉A的切线.故A选项不符合题意.∵∠B-∠C=∠A,∴∠B=∠C+∠A.∴∠B=90°.∴BC为☉A的切线.故B选项不符合题意.∵AB2+BC2=AC2,∴△ABC是以∠B为直角的直角三角形.∴AB⊥BC.∴BC为☉A的切线.故C选项不符合题意.故选D.
7.(1)证明:如图,连接CD,OD.
∵AC是☉O的直径,
∴∠ADC=90°.∴∠CDB=90°.
又∵EB=EC,
∴DE为Rt△DCB斜边的中线.
∴DE=CE=BC.
∴∠DCE=∠CDE.
∵OC=OD,∴∠OCD=∠ODC.
∴∠ODC+∠CDE=∠OCD+∠DCE=∠ACB=90°.
∴∠ODE=90°.
∴DE是☉O的切线.
(2)解:△ABC是等腰直角三角形.
理由:当以点O,D,E,C为顶点的四边形是正方形时,∠DEB=90°.又∵DE=BE,∴△DEB是等腰直角三角形,
则∠B=45°,∠A=45°.∴AC=BC.∴△ABC是等腰直角三角形.
课后提升
1.C 解析:∵AB是☉O的直径,∠BAP=90°,∴直线AP是☉O的切线,故甲同学的答案正确;
∵AB是☉O的直径,∴∠BAC+∠B=90°.若∠BAC=∠PAC,无法确定∠BAP的度数,故乙同学的答案错误;
若∠BAC=∠P,∴∠P+∠B=90°,即∠BAP=90°.∴直线AP是☉O的切线,故丙同学的答案正确.故选C.
2.B 解析:如图所示,连接OD,AD.
根据题意,得OA=OB=OD=AB=×8=4.∵∠B=30°,OD⊥CD,∠ADB=90°,∴∠OAD=60°,∠ADC=30°.在Rt△ACD中,AD=4,∠ADC=30°.∴AC=2,CD===2.故选B.
3.C 解析:如图所示,过点A,B分别作y轴,x轴的垂线,垂足分别为E,D,AE,BD交于点C.
根据题意,B的横坐标为1,A的纵坐标为1,设A(k,1),B(1,k).∴C(1,1).∴AC=k-1,BC=k-1.又∵∠ACB=90°,AB=3,∴=.∴k-1=3(负值已舍去),解得k=4.故选C.
4.48 解析:如图,连接OC.
∵PC是☉O的切线,∴OC⊥PC.在Rt△OCP中,tan P=,设OC=7x,则CP=24x,PO=64-7x.在Rt△PCO中,根据勾股定理,得PO2=PC2+OC2,即(64-7x)2=(24x)2+(7x)2,解得x1=2,x2=-(舍).∴PC=24×2=48.
5.(1)证明:如图,连接OD.
∵半圆O与AB相切于点D,
∴OD⊥AB.
∵∠ACB=90°,
∴∠ODB=∠OCB=90°.
∵OD=OC,OB=OB,
∴Rt△ODB≌Rt△OCB(HL).
∴BD=BC.
(2)解:∵∠A=30°,∠ACB=90°,
∴∠ABC=60°.
∵Rt△ODB≌Rt△OCB,
∴∠CBO=∠DBO=∠ABC=30°.
∵OC=1,
在Rt△BCO中,tan 30°=.
∴BC==.
在Rt△ABC中,sin 30°=.
∴AB==2.
6.(1)证明:如图,连接OC.
∵直线DC是☉O的切线,
∴OC⊥DE.
∵AE⊥DC,
∴OC∥AE.
∴∠OCA=∠CAE.
∵OA=OC,
∴∠OCA=∠CAO.
∴∠CAO=∠CAE,
即AC平分∠BAE.
(2)解:如图,过点O作OF⊥AC于点F,则CF=AC=.
∵∠OCE=∠OCF+∠ACE=90°,∠OCF+∠COF=90°,
∴∠ACE=∠COF.
∴tan∠COF=tan∠ACE=.
∴==.
∴OF=.
∴OC==,
即☉O的半径为.
7.(1)证明:∵AB∥CE,
∴∠ABD=∠CED,∠BAD=∠ECD.
又AD=CD,
∴△ABD≌△CED(AAS).
∴AB=CE.
∴四边形ABCE是平行四边形.
∴AE∥BC.
如图,过点A作AH⊥BC于点H.
又∵AB=AC,
∴AH为BC的垂直平分线.
∴点O在AH上.
∴AH⊥AE,
即OA⊥AE.又点A在☉O上,
∴AE为☉O的切线.
(2)解:如图,过点D作DM⊥BC于点M,连接OB.
∵AH为BC的垂直平分线,
∴BH=HC=BC=3.
∴OH===4.
∴AH=OA+OH=5+4=9.
∴AB=AC===3.
∴CD=AC=.
∵AH⊥BC,DM⊥BC,
∴DM∥AH.∴△CMD∽△CHA.
又AD=CD,
∴===.
∴MH=HC=,
DM=AH=.
∴BM=BH+MH=3+=.
∴BD==
=.
∵∠CFD=∠BAD,∠FDC=∠ADB,
∴△FCD∽△ABD.
∴=.∴=.
∴FC=5.
切线的性质
1.如图,AB是☉O的直径,AC是☉O的弦,过点C的切线交AB的延长线于点D,若∠D=32°,则
∠BAC的度数是 ( )
A.16° B.24° C.26° D.29°
2.如图,AC是☉O的切线,B为切点,连接OA,OC.若∠A=30°,AB=2,BC=3,则OC的长度是( )
A.3 B.2 C. D.6
3.如图,AB切☉O于点B,连接OA交☉O于点C,BD∥OA交☉O于点D,连接CD,若∠OCD=25°,则∠A的度数为 ( )
A.25° B.35° C.40° D.45°
4.如图,AD是☉O的直径,AB是☉O的弦,BC与☉O相切于点B,连接OB,若∠ABC=65°,则∠BOD的度数为 .
切线的判定
5.如图,已知☉O的半径为5,直线AB经过☉O上一点P,下列条件不能判定直线AB与☉O相切的是 ( )
A.OP=5
B.∠APO=∠BPO
C.点O到直线AB的距离是5
D.OP⊥AB
6.如图,点B在☉A 上,点C在☉A外,下列条件不能判定 BC是☉A的切线的是( )
A.∠A=50°,∠C=40°
B.∠B-∠C=∠A
C.AB2 +BC2 =AC2
D.☉A与AC的交点是AC的中点
7.如图,在Rt△ABC中,∠ACB=90°,以AC为直径的☉O与AB边交于点D,EB=EC.
(1)求证:DE是☉O的切线.
(2)若以点O,D,E,C为顶点的四边形是正方形,试判断△ABC的形状,并说明理由.
1.有一道题目:“如图,AB是☉O的直径,要使直线AP是☉O的切线,需添加的条件是 (写一个条件即可).”下面是三位同学写的答案,则下列判断正确的是 ( )
甲:∠BAP=90°;乙:∠BAC=∠PAC;
丙:∠BAC=∠P.
A.只有甲同学的答案正确 B.只有乙同学的答案正确
C.只有甲、丙同学的答案正确 D.三位同学的答案都正确
2.如图,AB是☉O的直径,CD是☉O的切线,D为切点,AC⊥CD,垂足为C,连接BD.若AB=8,且
∠B=30°,则CD的长为 ( )
A.2 B.2 C.4 D.4
3.如图,在平面直角坐标系中,点A,B在函数y=(k>0,x>0)的图像上,分别以点A,B为圆心,1为半径作圆,当☉A与x轴相切、☉B与y轴相切时,连接AB,AB=3,则k的值为 ( )
A.3 B.3 C.4 D.6
4.如图,AB是☉O的直径,P是AB延长线上的一点,PC是☉O的切线,C为切点.若PA=64,tan P=,则PC= .
5.如图,在Rt△ABC中,∠ACB=90°,点O在边AC上,以点O为圆心,OC为半径的半圆与斜边AB相切于点D,交OA于点E,连接OB.
(1)求证:BD=BC.
(2)已知OC=1,∠A=30°,求AB的长.
6.如图,已知AB是☉O的直径,直线DC是☉O的切线,切点为C,AE⊥DC,垂足为E,连接AC.
(1)求证:AC平分∠BAE.
(2)若AC=5,tan∠ACE=,求☉O的半径.
7.(运算能力)如图,等腰三角形ABC内接于☉O,AB=AC,BD是边AC上的中线,过点C作AB的平行线交BD的延长线于点E,BE交☉O于点F,连接AE,FC.
(1)求证:AE为☉O的切线.
(2)若☉O的半径为5,BC=6,求FC的长.
【详解答案】
课堂达标
1.D 解析:如图,连接OC.
∵CD与☉O相切于点C,∴CD⊥OC.∴∠OCD=90°.∵∠D=32°,∴∠DOC=90°-∠D=90°-32°=58°.
∴∠BAC=∠DOC=×58°=29°.故选D.
2.C 解析:如图,连接OB.∵AC是☉O的切线,B为切点,∴OB⊥AC.∵∠A=30°,AB=2,∴在Rt△OAB中,OB=AB·tan A=2=2.∵BC=3,∴在Rt△OBC中,OC==.故选C.
3.C 解析:如图,连接OB.
∵AB切☉O于点B,∴∠ABO=90°.∵BD∥OA, ∠OCD=25°,∴∠CDB=25°.∴∠BOC=2∠BDC=50°.∴∠A=40°.故选C.
4.50° 解析:∵BC与☉O相切于点B,∴∠OBC=90°.∵∠ABC=65°,∴∠OBA=90°-65°=25°.
∵OB=OA,∴∠A=∠OBA=25°.∴∠BOD=2×25°=50°.
5.A 解析:A.OP=5,不能判定直线AB与☉O相切,符合题意;B.由∠APO=∠BPO,得到OP⊥AB,且点P在☉O上,能判定直线AB与☉O相切,不符合题意;C.点O到直线AB的距离是5,等于半径,能判定直线AB与☉O相切,不符合题意;D.OP⊥AB且点P在☉O上,能判定直线AB与☉O相切,不符合题意.故选A.
6.D 解析:∵∠A=50°,∠C=40°,∴∠B=90°.∴BC为☉A的切线.故A选项不符合题意.∵∠B-∠C=∠A,∴∠B=∠C+∠A.∴∠B=90°.∴BC为☉A的切线.故B选项不符合题意.∵AB2+BC2=AC2,∴△ABC是以∠B为直角的直角三角形.∴AB⊥BC.∴BC为☉A的切线.故C选项不符合题意.故选D.
7.(1)证明:如图,连接CD,OD.
∵AC是☉O的直径,
∴∠ADC=90°.∴∠CDB=90°.
又∵EB=EC,
∴DE为Rt△DCB斜边的中线.
∴DE=CE=BC.
∴∠DCE=∠CDE.
∵OC=OD,∴∠OCD=∠ODC.
∴∠ODC+∠CDE=∠OCD+∠DCE=∠ACB=90°.
∴∠ODE=90°.
∴DE是☉O的切线.
(2)解:△ABC是等腰直角三角形.
理由:当以点O,D,E,C为顶点的四边形是正方形时,∠DEB=90°.又∵DE=BE,∴△DEB是等腰直角三角形,
则∠B=45°,∠A=45°.∴AC=BC.∴△ABC是等腰直角三角形.
课后提升
1.C 解析:∵AB是☉O的直径,∠BAP=90°,∴直线AP是☉O的切线,故甲同学的答案正确;
∵AB是☉O的直径,∴∠BAC+∠B=90°.若∠BAC=∠PAC,无法确定∠BAP的度数,故乙同学的答案错误;
若∠BAC=∠P,∴∠P+∠B=90°,即∠BAP=90°.∴直线AP是☉O的切线,故丙同学的答案正确.故选C.
2.B 解析:如图所示,连接OD,AD.
根据题意,得OA=OB=OD=AB=×8=4.∵∠B=30°,OD⊥CD,∠ADB=90°,∴∠OAD=60°,∠ADC=30°.在Rt△ACD中,AD=4,∠ADC=30°.∴AC=2,CD===2.故选B.
3.C 解析:如图所示,过点A,B分别作y轴,x轴的垂线,垂足分别为E,D,AE,BD交于点C.
根据题意,B的横坐标为1,A的纵坐标为1,设A(k,1),B(1,k).∴C(1,1).∴AC=k-1,BC=k-1.又∵∠ACB=90°,AB=3,∴=.∴k-1=3(负值已舍去),解得k=4.故选C.
4.48 解析:如图,连接OC.
∵PC是☉O的切线,∴OC⊥PC.在Rt△OCP中,tan P=,设OC=7x,则CP=24x,PO=64-7x.在Rt△PCO中,根据勾股定理,得PO2=PC2+OC2,即(64-7x)2=(24x)2+(7x)2,解得x1=2,x2=-(舍).∴PC=24×2=48.
5.(1)证明:如图,连接OD.
∵半圆O与AB相切于点D,
∴OD⊥AB.
∵∠ACB=90°,
∴∠ODB=∠OCB=90°.
∵OD=OC,OB=OB,
∴Rt△ODB≌Rt△OCB(HL).
∴BD=BC.
(2)解:∵∠A=30°,∠ACB=90°,
∴∠ABC=60°.
∵Rt△ODB≌Rt△OCB,
∴∠CBO=∠DBO=∠ABC=30°.
∵OC=1,
在Rt△BCO中,tan 30°=.
∴BC==.
在Rt△ABC中,sin 30°=.
∴AB==2.
6.(1)证明:如图,连接OC.
∵直线DC是☉O的切线,
∴OC⊥DE.
∵AE⊥DC,
∴OC∥AE.
∴∠OCA=∠CAE.
∵OA=OC,
∴∠OCA=∠CAO.
∴∠CAO=∠CAE,
即AC平分∠BAE.
(2)解:如图,过点O作OF⊥AC于点F,则CF=AC=.
∵∠OCE=∠OCF+∠ACE=90°,∠OCF+∠COF=90°,
∴∠ACE=∠COF.
∴tan∠COF=tan∠ACE=.
∴==.
∴OF=.
∴OC==,
即☉O的半径为.
7.(1)证明:∵AB∥CE,
∴∠ABD=∠CED,∠BAD=∠ECD.
又AD=CD,
∴△ABD≌△CED(AAS).
∴AB=CE.
∴四边形ABCE是平行四边形.
∴AE∥BC.
如图,过点A作AH⊥BC于点H.
又∵AB=AC,
∴AH为BC的垂直平分线.
∴点O在AH上.
∴AH⊥AE,
即OA⊥AE.又点A在☉O上,
∴AE为☉O的切线.
(2)解:如图,过点D作DM⊥BC于点M,连接OB.
∵AH为BC的垂直平分线,
∴BH=HC=BC=3.
∴OH===4.
∴AH=OA+OH=5+4=9.
∴AB=AC===3.
∴CD=AC=.
∵AH⊥BC,DM⊥BC,
∴DM∥AH.∴△CMD∽△CHA.
又AD=CD,
∴===.
∴MH=HC=,
DM=AH=.
∴BM=BH+MH=3+=.
∴BD==
=.
∵∠CFD=∠BAD,∠FDC=∠ADB,
∴△FCD∽△ABD.
∴=.∴=.
∴FC=5.
