29.4切线长定理 课时作业(含详解) 2024-2025学年数学冀教版九年级下册
文档属性
| 名称 | 29.4切线长定理 课时作业(含详解) 2024-2025学年数学冀教版九年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 222.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-26 00:00:00 | ||
图片预览



文档简介
29.4切线长定理*
切线长定理
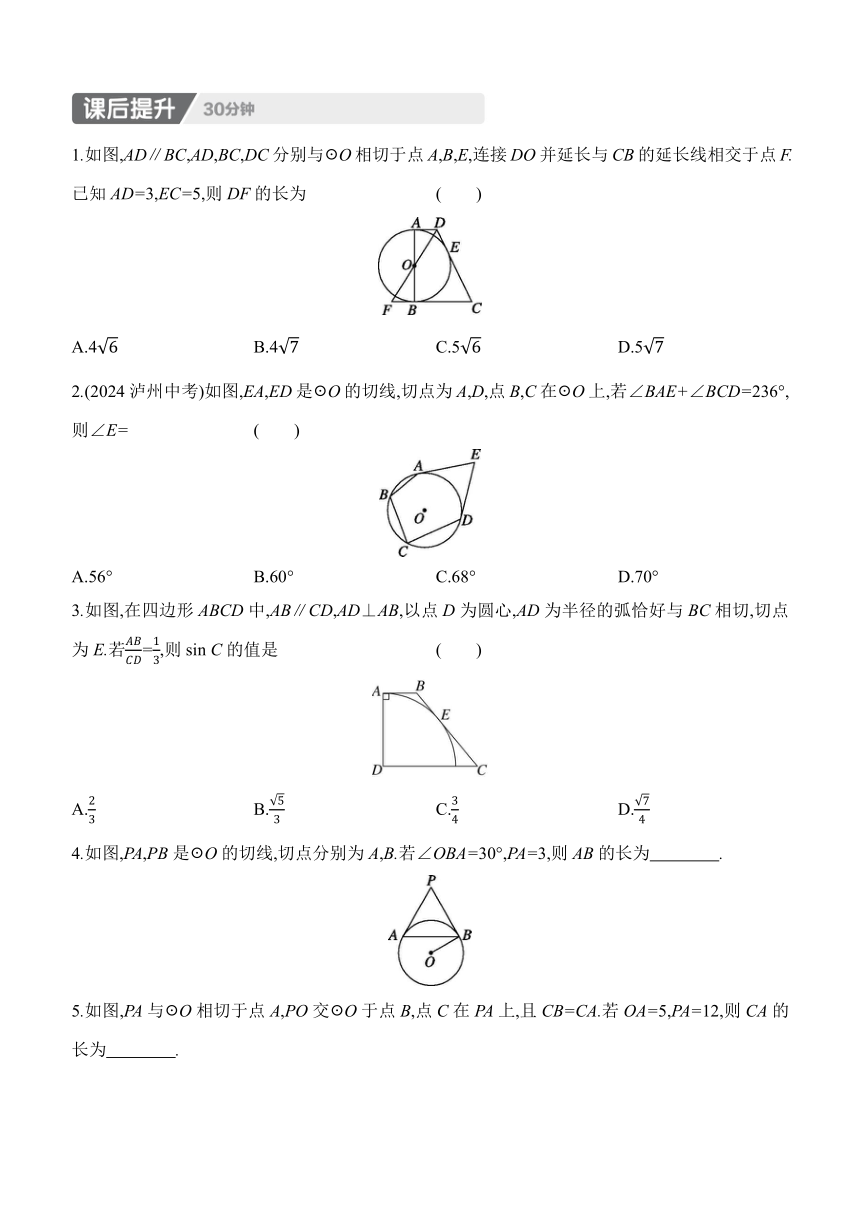
1.如图,AB,AC,BD是☉O的切线,切点分别是P,C,D.若AB=5,AC=3,则BD的长是 ( )
A.4 B.3 C.2 D.1
2.如图,PA,PB分别切☉O于点A,B,MN切☉O于点C,分别交PA,PB于点M,N,若PA=7.5 cm,则△PMN的周长是 ( )
A.7.5 cm B.10 cm C.12.5 cm D.15 cm
3.如图,PA,PB分别切☉O于点A,B,连接AB,若AP=3 cm,∠P=60°,则AB的长为 cm.
4.如图,AC是☉O的直径,PA切☉O于点A,PB切☉O于点B,且∠APB=60°.
(1)求∠BAC的度数.
(2)若PA=1,求点O到弦AB的距离.
三角形的内切圆与内心
5.如图,☉O是△ABC的内切圆,D,E是切点,∠A=50°,∠C=60°,则∠DOE的度数为 ( )
A.70° B.110° C.120° D.130°
6.在△ABC中,BC=3,AC=4,下列说法错误的是 ( )
A.1B.S△ABC≤6
C.△ABC内切圆的半径r<1
D.当AB=时,△ABC是直角三角形
7.如图,点O是△ABC的外心,点I是△ABC的内心,连接OI,OB,IA.若∠CAI=35°,则∠OBC的度数为 ( )
A.15° B.17.5° C.20° D.25°
8.如图,已知☉O是Rt△ABC的内切圆,D,E,F为切点,∠C是直角,AC=6,BC=8.求☉O的半径r.
1.如图,AD∥BC,AD,BC,DC分别与☉O相切于点A,B,E,连接DO并延长与CB的延长线相交于点F.已知AD=3,EC=5,则DF的长为 ( )
A.4 B.4 C.5 D.5
2.(2024泸州中考)如图,EA,ED是☉O的切线,切点为A,D,点B,C在☉O上,若∠BAE+∠BCD=236°,则∠E= ( )
A.56° B.60° C.68° D.70°
3.如图,在四边形ABCD中,AB∥CD,AD⊥AB,以点D为圆心,AD为半径的弧恰好与BC相切,切点为E.若=,则sin C的值是 ( )
A. B. C. D.
4.如图,PA,PB是☉O的切线,切点分别为A,B.若∠OBA=30°,PA=3,则AB的长为 .
5.如图,PA与☉O相切于点A,PO交☉O于点B,点C在PA上,且CB=CA.若OA=5,PA=12,则CA的长为 .
6.如图,在Rt△ABC中,∠C=90°,AC=12,BC=5,☉O为Rt△ABC的内切圆,则图中阴影部分的面积为 .(结果保留π)
7.已知PA,PB分别与☉O相切于点A,B,∠APB=80°,C为☉O上一点.
(1)如图1,求∠ACB的大小.
(2)如图2,AE为☉O的直径,AE与BC相交于点D.若AB=AD,求∠EAC的大小.
图1 图2
8.(几何直观)如图,点I是△ABC的内心,线段AI的延长线交△ABC的外接圆于点D,交BC边于点E.
(1)求证:ID=BD.
(2)设△ABC的外接圆的半径为5,ID=6,AD=x,DE=y,当点A在优弧BC上运动时,求y与x之间的函数关系式,并指出自变量x的取值范围.
【详解答案】
课堂达标
1.C 解析:∵AC,AP为☉O的切线,∴AC=AP=3.∵BP,BD为☉O的切线,∴BP=BD,∴BD=PB=AB-AP=5-3=2.故选C.
2.D 解析:∵直线PA,PB,MN分别与☉O相切于点A,B,C,∴PA=PB,MA=MC,NC=NB.∴△PMN的周长=PM+PN+MC+NC=PM+MA+PN+NB=PA+PB=7.5+7.5=15(cm).故选D.
3.3 解析:∵PA,PB分别切☉O于点A,B,∴PA=PB.又∵∠P=60°,∴△APB为等边三角形.∴AB=AP=3 cm.
4.解:(1)∵PA切☉O于点A,PB切☉O于点B,
∴PA=PB,∠PAC=90°.
∵∠APB=60°,
∴△APB是等边三角形.
∴∠BAP=60°.
∴∠BAC=90°-∠BAP=30°.
(2)如图,过点O作OD⊥AB于点D.
∴AD=BD=AB.
由(1),得△APB是等边三角形,
∴AB=PA=1.
∴AD=.
∵∠BAC=30°,
∴OD=AD·tan 30°==,
即点O到弦AB的距离为.
5.B 解析:∵∠BAC=50°,∠C=60°,∴∠B=180°-50°-60°=70°.∵E,D是切点,∴∠BDO=∠BEO=90°.
∴∠DOE=180°-∠B=110°.故选B.
6.C 解析:∵BC=3,AC=4,∴4-3∴(AB+BC+AC)≤6,
r≤,∵17.C 解析:如图,连接OC.∵点I是△ABC的内心,∠CAI=35°,∴∠BAC=2∠CAI=70°.∴∠BOC=2∠BAC=140°.∵OB=OC,∴∠OBC=∠OCB===20°.故选C.
8.解:连接OA,OB,OC,OD,OE,OF(图略).在Rt△ABC中,AC=6,BC=8,∴AB=10.∵☉O是Rt△ABC的内切圆,D,E,F为切点,∴OD⊥AB,OE⊥BC,OF⊥AC,且OD=OE=OF=r.∴S△ABC=S△ABO+S△ACO+S△BCO.∴=,∴r=2.
课后提升
1.A 解析:如图,连接OC,OE.
∵AD,BC,DC分别与☉O相切于点A,B,E,∴DE=AD=3,BC=CE=5,OE⊥CD,OA⊥AD,OB⊥BC.
∴∠OAD=∠OBF=90°,∠DEO=∠OEC=90°,CD=CE+DE=5+3=8.∵AD∥BC,∴∠ADO=∠F.
∵OA=OB,∴△OAD≌△OBF.∴OF=OD,BF=AD=3.∴CF=BF+BC=3+5=8.∴CD=CF.
∵OD=OF,∴OC⊥DF.∴∠DOC=∠DEO=90°.∴∠ODC+∠DOE=∠COE+
∠DOE=90°.∴∠ODC=∠COE.∵∠DEO=∠OEC=90°,∴△ODE∽△COE.∴=.∴OE2=CE·DE=5×3=15.
∴OE=.在Rt△ODE中,OD==2.∵OF=OD,∴DF=2OD=4.故选A.
2.C 解析:如图,连接AD.
∵四边形ABCD是☉O的内接四边形,∴∠BAD+∠BCD=180°.∵∠BAE+∠BCD=236°,∴∠BAE-
∠BAD=56°.∴∠EAD=56°.∵EA,ED是☉O的切线,根据切线长定理,得EA=ED.∴∠EAD=∠EDA=56°.
∴∠E=180°-∠EAD-∠EDA=180°-56°-56°=68°.故选C.
3.B 解析:如图,过点C作CF⊥AB交AB的延长线于点F,连接DE.
∵AD⊥AB,AB∥CD,∴∠FAD=∠ADC=∠F=90°.∴四边形ADCF为矩形,AF=DC,AD=FC.∴AB为☉D的切线.由题意,得BE为☉D的切线.∴DE⊥BC,AB=BE.∵=,∴设AB=BE=a,CD=3a,CE=x,则BF=AF-AB=CD-AB=2a,BC=BE+CE=a+x.在Rt△DEC中,DE2=CD2-CE2=9a2-x2.在Rt△BFC中,FC2=BC2-BF2=(a+x)2-(2a)2.
∵DE=DA=FC,∴9a2-x2=(a+x)2-(2a)2.解得x=2a或x=-3a(不合题意,舍去).
∴CE=2a.∴DE===a.∴sin C===.故选B.
4.3 解析:∵PA,PB是☉O的切线,∴PA=PB,∠OBP=90°.∵∠OBA=30°,∴∠PBA=60°.∴△PAB为等边三角形.
∴AB=PA=3.
5. 解析:如图,连接OC.∵PA与☉O相切于点A,∴∠OAC=90°.
∵∴△OAC≌△OBC(SSS).
∴∠OAC=∠OBC=90°.∴∠PAO=∠PBC=90°.∵∠P=∠P,∴△PAO∽△PBC.∴=.∵OA=5,PA=12,
∴PO==13.设CB=CA=x,则PC=PA-CA=12-x.∴=.解得x=.故CA的长为.
6.30-4π 解析:在Rt△ABC中,AC=12,BC=5,∴AB==13.∴S△ABC=AC·BC=30.∴△ABC的周长=AC+BC+AB=30.∴内切圆半径r===2.∴S☉O=πr2=4π.∴阴影部分的面积为S△ABC-S☉O=30-4π.
7.解:(1)连接OA,OB,如图1所示.
图1
∵PA,PB与☉O相切于点A,B,
∴∠OAP=∠OBP=90°.
∴∠AOB=360°-90°-90°-80°=100°.
∴∠ACB=∠AOB=50°.
(2)如图2,连接CE.
图2
∵AE为☉O的直径,
∴∠ACE=90°.
∵∠ACB=50°,
∴∠BCE=90°-50°=40°.
∴∠BAE=∠BCE=40°.
∵AB=AD,
∴∠ABD=∠ADB=70°.
∴∠EAC=∠ADB-∠ACB=20°.
8.(1)证明:∵点I是△ABC的内心,
∴∠BAD=∠CAD,∠ABI=∠CBI.
∵∠CBD=∠CAD,
∴∠BAD=∠CBD.
∴∠BID=∠ABI+∠BAD=∠CBI+∠CBD=∠IBD.
∴ID=BD.
(2)解:∵∠BAD=∠CBD=∠EBD,
∠D=∠D,
∴△ABD∽△BED.
∴=.
∴AD×DE=BD2=ID2.
∵ID=6,AD=x,DE=y,
∴xy=36.
又∵x=AD>ID=6,AD不大于圆的直径10,
∴6∴y与x之间的函数关系式是y=.
切线长定理
1.如图,AB,AC,BD是☉O的切线,切点分别是P,C,D.若AB=5,AC=3,则BD的长是 ( )
A.4 B.3 C.2 D.1
2.如图,PA,PB分别切☉O于点A,B,MN切☉O于点C,分别交PA,PB于点M,N,若PA=7.5 cm,则△PMN的周长是 ( )
A.7.5 cm B.10 cm C.12.5 cm D.15 cm
3.如图,PA,PB分别切☉O于点A,B,连接AB,若AP=3 cm,∠P=60°,则AB的长为 cm.
4.如图,AC是☉O的直径,PA切☉O于点A,PB切☉O于点B,且∠APB=60°.
(1)求∠BAC的度数.
(2)若PA=1,求点O到弦AB的距离.
三角形的内切圆与内心
5.如图,☉O是△ABC的内切圆,D,E是切点,∠A=50°,∠C=60°,则∠DOE的度数为 ( )
A.70° B.110° C.120° D.130°
6.在△ABC中,BC=3,AC=4,下列说法错误的是 ( )
A.1
C.△ABC内切圆的半径r<1
D.当AB=时,△ABC是直角三角形
7.如图,点O是△ABC的外心,点I是△ABC的内心,连接OI,OB,IA.若∠CAI=35°,则∠OBC的度数为 ( )
A.15° B.17.5° C.20° D.25°
8.如图,已知☉O是Rt△ABC的内切圆,D,E,F为切点,∠C是直角,AC=6,BC=8.求☉O的半径r.
1.如图,AD∥BC,AD,BC,DC分别与☉O相切于点A,B,E,连接DO并延长与CB的延长线相交于点F.已知AD=3,EC=5,则DF的长为 ( )
A.4 B.4 C.5 D.5
2.(2024泸州中考)如图,EA,ED是☉O的切线,切点为A,D,点B,C在☉O上,若∠BAE+∠BCD=236°,则∠E= ( )
A.56° B.60° C.68° D.70°
3.如图,在四边形ABCD中,AB∥CD,AD⊥AB,以点D为圆心,AD为半径的弧恰好与BC相切,切点为E.若=,则sin C的值是 ( )
A. B. C. D.
4.如图,PA,PB是☉O的切线,切点分别为A,B.若∠OBA=30°,PA=3,则AB的长为 .
5.如图,PA与☉O相切于点A,PO交☉O于点B,点C在PA上,且CB=CA.若OA=5,PA=12,则CA的长为 .
6.如图,在Rt△ABC中,∠C=90°,AC=12,BC=5,☉O为Rt△ABC的内切圆,则图中阴影部分的面积为 .(结果保留π)
7.已知PA,PB分别与☉O相切于点A,B,∠APB=80°,C为☉O上一点.
(1)如图1,求∠ACB的大小.
(2)如图2,AE为☉O的直径,AE与BC相交于点D.若AB=AD,求∠EAC的大小.
图1 图2
8.(几何直观)如图,点I是△ABC的内心,线段AI的延长线交△ABC的外接圆于点D,交BC边于点E.
(1)求证:ID=BD.
(2)设△ABC的外接圆的半径为5,ID=6,AD=x,DE=y,当点A在优弧BC上运动时,求y与x之间的函数关系式,并指出自变量x的取值范围.
【详解答案】
课堂达标
1.C 解析:∵AC,AP为☉O的切线,∴AC=AP=3.∵BP,BD为☉O的切线,∴BP=BD,∴BD=PB=AB-AP=5-3=2.故选C.
2.D 解析:∵直线PA,PB,MN分别与☉O相切于点A,B,C,∴PA=PB,MA=MC,NC=NB.∴△PMN的周长=PM+PN+MC+NC=PM+MA+PN+NB=PA+PB=7.5+7.5=15(cm).故选D.
3.3 解析:∵PA,PB分别切☉O于点A,B,∴PA=PB.又∵∠P=60°,∴△APB为等边三角形.∴AB=AP=3 cm.
4.解:(1)∵PA切☉O于点A,PB切☉O于点B,
∴PA=PB,∠PAC=90°.
∵∠APB=60°,
∴△APB是等边三角形.
∴∠BAP=60°.
∴∠BAC=90°-∠BAP=30°.
(2)如图,过点O作OD⊥AB于点D.
∴AD=BD=AB.
由(1),得△APB是等边三角形,
∴AB=PA=1.
∴AD=.
∵∠BAC=30°,
∴OD=AD·tan 30°==,
即点O到弦AB的距离为.
5.B 解析:∵∠BAC=50°,∠C=60°,∴∠B=180°-50°-60°=70°.∵E,D是切点,∴∠BDO=∠BEO=90°.
∴∠DOE=180°-∠B=110°.故选B.
6.C 解析:∵BC=3,AC=4,∴4-3
r≤,∵1
8.解:连接OA,OB,OC,OD,OE,OF(图略).在Rt△ABC中,AC=6,BC=8,∴AB=10.∵☉O是Rt△ABC的内切圆,D,E,F为切点,∴OD⊥AB,OE⊥BC,OF⊥AC,且OD=OE=OF=r.∴S△ABC=S△ABO+S△ACO+S△BCO.∴=,∴r=2.
课后提升
1.A 解析:如图,连接OC,OE.
∵AD,BC,DC分别与☉O相切于点A,B,E,∴DE=AD=3,BC=CE=5,OE⊥CD,OA⊥AD,OB⊥BC.
∴∠OAD=∠OBF=90°,∠DEO=∠OEC=90°,CD=CE+DE=5+3=8.∵AD∥BC,∴∠ADO=∠F.
∵OA=OB,∴△OAD≌△OBF.∴OF=OD,BF=AD=3.∴CF=BF+BC=3+5=8.∴CD=CF.
∵OD=OF,∴OC⊥DF.∴∠DOC=∠DEO=90°.∴∠ODC+∠DOE=∠COE+
∠DOE=90°.∴∠ODC=∠COE.∵∠DEO=∠OEC=90°,∴△ODE∽△COE.∴=.∴OE2=CE·DE=5×3=15.
∴OE=.在Rt△ODE中,OD==2.∵OF=OD,∴DF=2OD=4.故选A.
2.C 解析:如图,连接AD.
∵四边形ABCD是☉O的内接四边形,∴∠BAD+∠BCD=180°.∵∠BAE+∠BCD=236°,∴∠BAE-
∠BAD=56°.∴∠EAD=56°.∵EA,ED是☉O的切线,根据切线长定理,得EA=ED.∴∠EAD=∠EDA=56°.
∴∠E=180°-∠EAD-∠EDA=180°-56°-56°=68°.故选C.
3.B 解析:如图,过点C作CF⊥AB交AB的延长线于点F,连接DE.
∵AD⊥AB,AB∥CD,∴∠FAD=∠ADC=∠F=90°.∴四边形ADCF为矩形,AF=DC,AD=FC.∴AB为☉D的切线.由题意,得BE为☉D的切线.∴DE⊥BC,AB=BE.∵=,∴设AB=BE=a,CD=3a,CE=x,则BF=AF-AB=CD-AB=2a,BC=BE+CE=a+x.在Rt△DEC中,DE2=CD2-CE2=9a2-x2.在Rt△BFC中,FC2=BC2-BF2=(a+x)2-(2a)2.
∵DE=DA=FC,∴9a2-x2=(a+x)2-(2a)2.解得x=2a或x=-3a(不合题意,舍去).
∴CE=2a.∴DE===a.∴sin C===.故选B.
4.3 解析:∵PA,PB是☉O的切线,∴PA=PB,∠OBP=90°.∵∠OBA=30°,∴∠PBA=60°.∴△PAB为等边三角形.
∴AB=PA=3.
5. 解析:如图,连接OC.∵PA与☉O相切于点A,∴∠OAC=90°.
∵∴△OAC≌△OBC(SSS).
∴∠OAC=∠OBC=90°.∴∠PAO=∠PBC=90°.∵∠P=∠P,∴△PAO∽△PBC.∴=.∵OA=5,PA=12,
∴PO==13.设CB=CA=x,则PC=PA-CA=12-x.∴=.解得x=.故CA的长为.
6.30-4π 解析:在Rt△ABC中,AC=12,BC=5,∴AB==13.∴S△ABC=AC·BC=30.∴△ABC的周长=AC+BC+AB=30.∴内切圆半径r===2.∴S☉O=πr2=4π.∴阴影部分的面积为S△ABC-S☉O=30-4π.
7.解:(1)连接OA,OB,如图1所示.
图1
∵PA,PB与☉O相切于点A,B,
∴∠OAP=∠OBP=90°.
∴∠AOB=360°-90°-90°-80°=100°.
∴∠ACB=∠AOB=50°.
(2)如图2,连接CE.
图2
∵AE为☉O的直径,
∴∠ACE=90°.
∵∠ACB=50°,
∴∠BCE=90°-50°=40°.
∴∠BAE=∠BCE=40°.
∵AB=AD,
∴∠ABD=∠ADB=70°.
∴∠EAC=∠ADB-∠ACB=20°.
8.(1)证明:∵点I是△ABC的内心,
∴∠BAD=∠CAD,∠ABI=∠CBI.
∵∠CBD=∠CAD,
∴∠BAD=∠CBD.
∴∠BID=∠ABI+∠BAD=∠CBI+∠CBD=∠IBD.
∴ID=BD.
(2)解:∵∠BAD=∠CBD=∠EBD,
∠D=∠D,
∴△ABD∽△BED.
∴=.
∴AD×DE=BD2=ID2.
∵ID=6,AD=x,DE=y,
∴xy=36.
又∵x=AD>ID=6,AD不大于圆的直径10,
∴6
