32. 1投影 课时作业(含答案) 2024-2025学年数学冀教版九年级下册
文档属性
| 名称 | 32. 1投影 课时作业(含答案) 2024-2025学年数学冀教版九年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 221.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-26 00:00:00 | ||
图片预览


文档简介
32. 1投影
中心投影
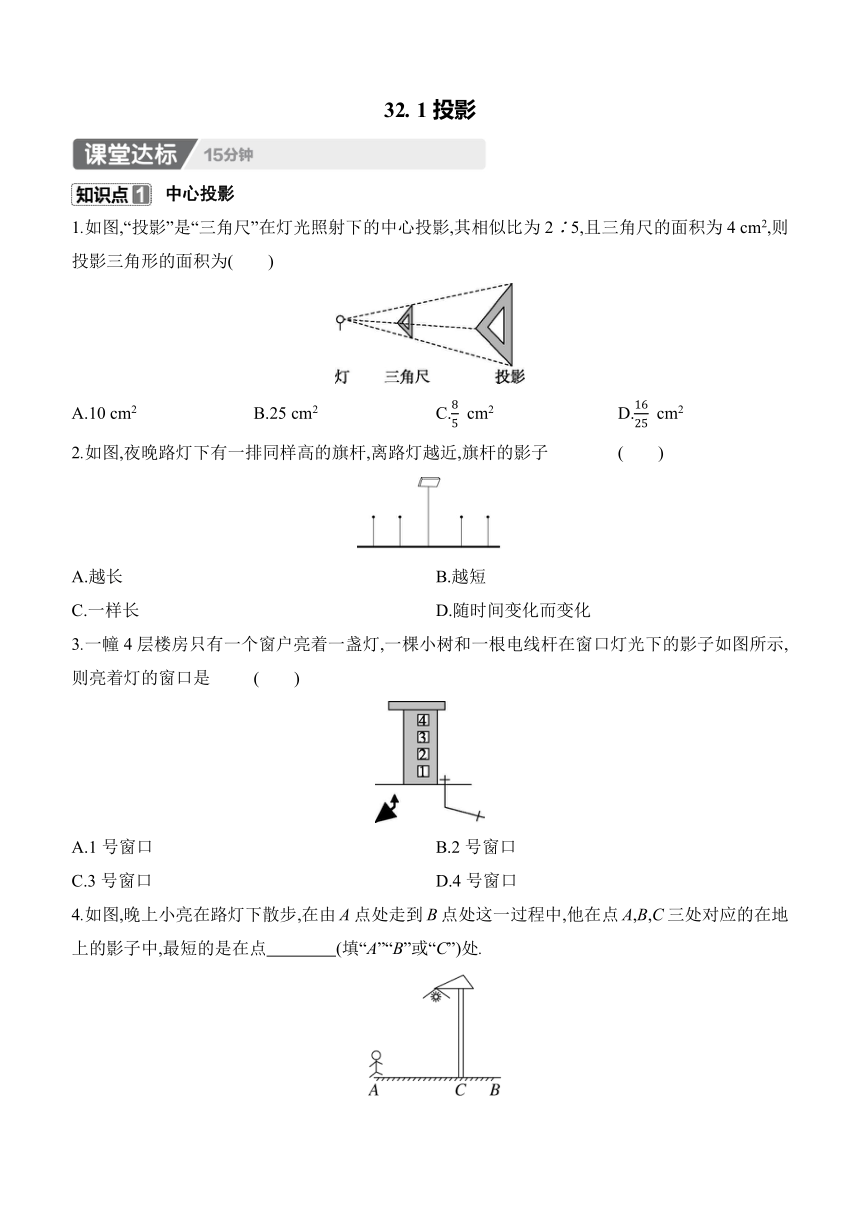
1.如图,“投影”是“三角尺”在灯光照射下的中心投影,其相似比为2∶5,且三角尺的面积为4 cm2,则投影三角形的面积为( )
A.10 cm2 B.25 cm2 C. cm2 D. cm2
2.如图,夜晚路灯下有一排同样高的旗杆,离路灯越近,旗杆的影子 ( )
A.越长 B.越短
C.一样长 D.随时间变化而变化
3.一幢4层楼房只有一个窗户亮着一盏灯,一棵小树和一根电线杆在窗口灯光下的影子如图所示,则亮着灯的窗口是 ( )
A.1号窗口 B.2号窗口
C.3号窗口 D.4号窗口
4.如图,晚上小亮在路灯下散步,在由A点处走到B点处这一过程中,他在点A,B,C三处对应的在地上的影子中,最短的是在点 (填“A”“B”或“C”)处.
平行投影
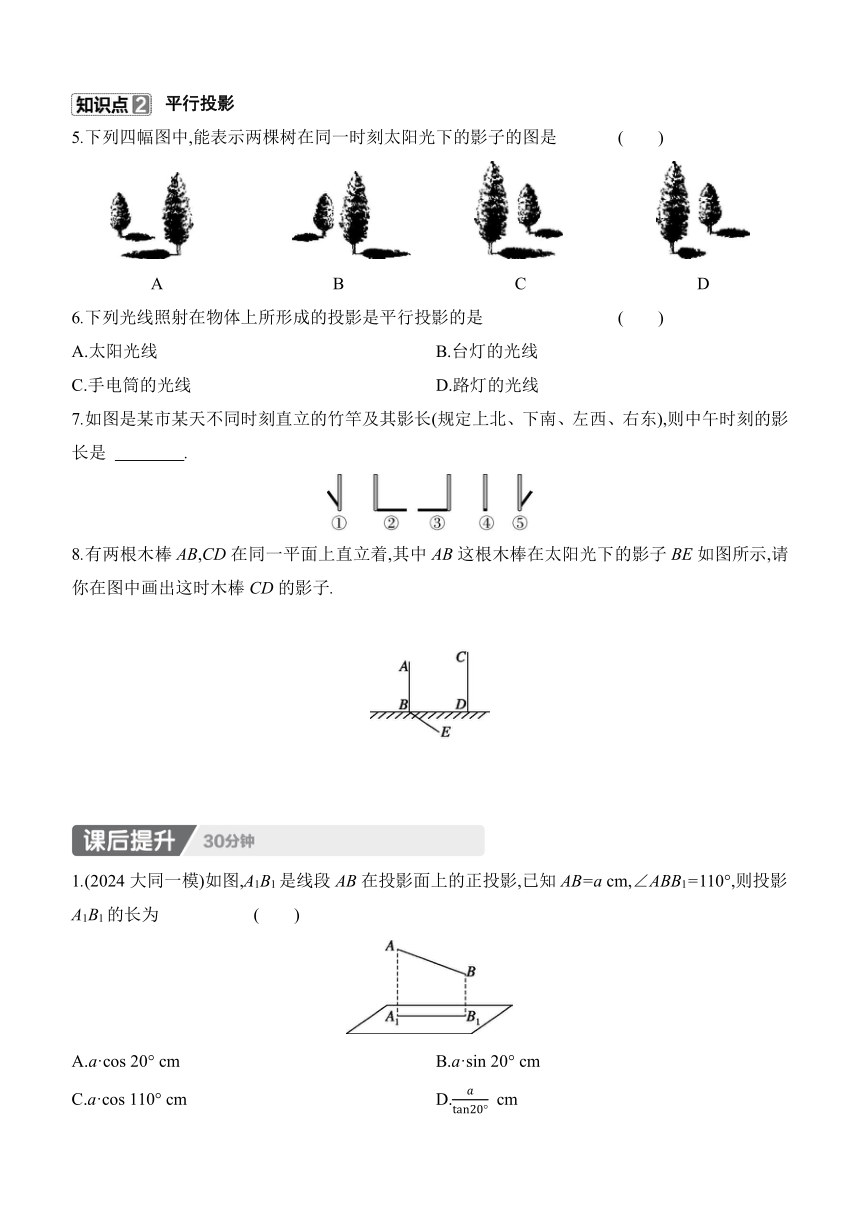
5.下列四幅图中,能表示两棵树在同一时刻太阳光下的影子的图是 ( )
A B C D
6.下列光线照射在物体上所形成的投影是平行投影的是 ( )
A.太阳光线 B.台灯的光线
C.手电筒的光线 D.路灯的光线
7.如图是某市某天不同时刻直立的竹竿及其影长(规定上北、下南、左西、右东),则中午时刻的影长是 .
8.有两根木棒AB,CD在同一平面上直立着,其中AB这根木棒在太阳光下的影子BE如图所示,请你在图中画出这时木棒CD的影子.
1.(2024大同一模)如图,A1B1是线段AB在投影面上的正投影,已知AB=a cm,∠ABB1=110°,则投影A1B1的长为 ( )
A.a·cos 20° cm B.a·sin 20° cm
C.a·cos 110° cm D. cm
2.手影游戏利用的物理原理:光是沿直线传播的.图中小狗手影就是我们小时候常玩的游戏.在一次游戏中,小明距离墙壁1 m,爸爸拿着的光源与小明的距离为2 m.在小明不动的情况下,要使小狗手影的高度增加一倍,则光源与小明的距离应 ( )
A.减少 m B.增加 m
C.减少 m D.增加 m
3.甲、乙两人沿着如图所示的平行四边形空地边缘进行跑步比赛,二人同时从点B出发,沿着平行四边形边缘顺时针跑步,且甲的速度是乙的速度的2倍.当甲到达点E,乙到达点F时,甲、乙的影子(太阳光照射)刚好在同一条直线上,此时,点B处一根杆子的影子(太阳光照射)刚好在对角线BD上,则CE的长为 ( )
A.4 m B.8 m C.12 m D.16 m
4.树AB和木杆CD同一时刻在阳光下的投影如图所示,木杆CD高2 m,影子DF长3 m.若树的影子BE长7 m,则树AB高多少米
5.(几何直观)如图所示,不透明圆锥DO放在水平面上,在A处灯光的照射下形成影子.设BP过底面的圆心,已知圆锥的高为2 m,底面半径为2 m,BE=4 m.
(1)求∠B的度数.
(2)若∠ACP=2∠B,求光源A到水平面的距离(答案用含根号的式子表示).
【详解答案】
课堂达标
1.B 解析:∵位似图形由三角尺与其灯光照射下的中心投影组成,相似比为2∶5,三角尺的面积为4 cm2,∴投影三角形的面积为25 cm2.故选B.
2.B 解析:由图(如图)易得AB3.B 解析:如图所示.故选B.
4.C 解析:小亮在路灯下由远及近向路灯靠近时,其影子应该逐渐变短;在路灯下由近及远离开路灯时,其影子应该逐渐变长.故他在点A,B,C三处对应的在地上的影子,其中影子最短的是在点C处.
5.C 解析:A.两棵树的影子的方向相反,不可能为同一时刻阳光下的影子,所以A选项错误;B.两棵树的影子的方向相反,不可能为同一时刻阳光下的影子,所以B选项错误;C.在同一时刻阳光下,树高与影子成正比,所以C选项正确,D选项错误.故选C.
6.A 解析:判断投影是平行投影的方法是看光线是不是平行的,如果光线是平行的,所得到的投影就是平行投影.四个选项中只有太阳光是平行光线,故太阳光线照射在物体上所形成的投影是平行投影.故选A.
7.④ 解析:根据从早晨到傍晚物体影子的指向是西-西北-北-东北-东,影长由长变短,再变长的规律可知时间顺序为③①④⑤②,中午时刻的影长为④.
8.解:如图所示,首先连接AE,过点C作AE的平行线;然后再过点D作BE的平行线,相交于点F,DF即为所求.
课后提升
1.A 解析:如图,过点B作BC⊥AA1,垂足为C.
∵A1B1是线段AB在投影面上的正投影,∴AA1⊥A1B1,BB1⊥A1B1.∴四边形A1B1BC为矩形.∴BC=A1B1.∠ACB=∠CBB1=90°,∴∠ABC=∠ABB1-∠CBB1=20°.∴BC=AB·cos 20°.∴A1B1=AB·cos 20°=a·cos 20°(cm).故选A.
2.A 解析:如图1,点O为光源,AB表示小明的手,CD表示小狗手影,则AB∥CD,过点O作OE⊥AB于点E,延长OE交CD于点F,则OF⊥CD.
图1
∵AB∥CD,∴△AOB∽△COD,则=.∵EF=1 m,OE=2 m,则OF=3 m.∴==.设AB=2k m,CD=3k m,∵在小明不动的情况下,要使小狗手影的高度增加一倍,如图2所示.
图2
∴AB=2k m,C'D'=6k m,E'F'=1 m,△AO'B∽△C'O'D'.∴==.则O'F'-O'E'=2O'E'=E'F'.∴O'E'= m.∴光源与小明的距离变化为OE-O'E'=2-=(m).故选A.
3.B 解析:如图,连接EF.根据题意,可得EF∥DB,故=.∴=.∴CF=2CE.设乙的速度为x,故甲的速度为2x,根据题意,甲所走的路程为BC→CE,即40+CE,乙所走的路程为BF,即40-CF,故可得=,解得CE=
8 m.故选B.
4.解:∵AB∥CD,AE∥CF,
∴∠ABE=∠CDF,∠AEB=∠CFD,
∴△ABE∽△CDF,
∴AB∶BE=CD∶DF.
∴AB∶7=2∶3,
解得AB=.
故树AB高 m.
5.解:(1)如图,圆锥的高DO=2 m,在Rt△DOB中,OB=BE+EO=4+2=6(m),
∴tan B===.
∴∠B=30°.
(2)如图,过点A作AF⊥BP,垂足为F.
∵∠B=30°,
∴∠ACP=2∠B=60°.
又∵∠ACP=∠B+∠BAC,
∴∠B=∠BAC.
∴AC=BC=BE+EC=8 m.
在Rt△ACF中,AF=AC·sin∠ACF=8·sin 60°=4(m).
故光源A到水平面的距离为4 m.
中心投影
1.如图,“投影”是“三角尺”在灯光照射下的中心投影,其相似比为2∶5,且三角尺的面积为4 cm2,则投影三角形的面积为( )
A.10 cm2 B.25 cm2 C. cm2 D. cm2
2.如图,夜晚路灯下有一排同样高的旗杆,离路灯越近,旗杆的影子 ( )
A.越长 B.越短
C.一样长 D.随时间变化而变化
3.一幢4层楼房只有一个窗户亮着一盏灯,一棵小树和一根电线杆在窗口灯光下的影子如图所示,则亮着灯的窗口是 ( )
A.1号窗口 B.2号窗口
C.3号窗口 D.4号窗口
4.如图,晚上小亮在路灯下散步,在由A点处走到B点处这一过程中,他在点A,B,C三处对应的在地上的影子中,最短的是在点 (填“A”“B”或“C”)处.
平行投影
5.下列四幅图中,能表示两棵树在同一时刻太阳光下的影子的图是 ( )
A B C D
6.下列光线照射在物体上所形成的投影是平行投影的是 ( )
A.太阳光线 B.台灯的光线
C.手电筒的光线 D.路灯的光线
7.如图是某市某天不同时刻直立的竹竿及其影长(规定上北、下南、左西、右东),则中午时刻的影长是 .
8.有两根木棒AB,CD在同一平面上直立着,其中AB这根木棒在太阳光下的影子BE如图所示,请你在图中画出这时木棒CD的影子.
1.(2024大同一模)如图,A1B1是线段AB在投影面上的正投影,已知AB=a cm,∠ABB1=110°,则投影A1B1的长为 ( )
A.a·cos 20° cm B.a·sin 20° cm
C.a·cos 110° cm D. cm
2.手影游戏利用的物理原理:光是沿直线传播的.图中小狗手影就是我们小时候常玩的游戏.在一次游戏中,小明距离墙壁1 m,爸爸拿着的光源与小明的距离为2 m.在小明不动的情况下,要使小狗手影的高度增加一倍,则光源与小明的距离应 ( )
A.减少 m B.增加 m
C.减少 m D.增加 m
3.甲、乙两人沿着如图所示的平行四边形空地边缘进行跑步比赛,二人同时从点B出发,沿着平行四边形边缘顺时针跑步,且甲的速度是乙的速度的2倍.当甲到达点E,乙到达点F时,甲、乙的影子(太阳光照射)刚好在同一条直线上,此时,点B处一根杆子的影子(太阳光照射)刚好在对角线BD上,则CE的长为 ( )
A.4 m B.8 m C.12 m D.16 m
4.树AB和木杆CD同一时刻在阳光下的投影如图所示,木杆CD高2 m,影子DF长3 m.若树的影子BE长7 m,则树AB高多少米
5.(几何直观)如图所示,不透明圆锥DO放在水平面上,在A处灯光的照射下形成影子.设BP过底面的圆心,已知圆锥的高为2 m,底面半径为2 m,BE=4 m.
(1)求∠B的度数.
(2)若∠ACP=2∠B,求光源A到水平面的距离(答案用含根号的式子表示).
【详解答案】
课堂达标
1.B 解析:∵位似图形由三角尺与其灯光照射下的中心投影组成,相似比为2∶5,三角尺的面积为4 cm2,∴投影三角形的面积为25 cm2.故选B.
2.B 解析:由图(如图)易得AB
4.C 解析:小亮在路灯下由远及近向路灯靠近时,其影子应该逐渐变短;在路灯下由近及远离开路灯时,其影子应该逐渐变长.故他在点A,B,C三处对应的在地上的影子,其中影子最短的是在点C处.
5.C 解析:A.两棵树的影子的方向相反,不可能为同一时刻阳光下的影子,所以A选项错误;B.两棵树的影子的方向相反,不可能为同一时刻阳光下的影子,所以B选项错误;C.在同一时刻阳光下,树高与影子成正比,所以C选项正确,D选项错误.故选C.
6.A 解析:判断投影是平行投影的方法是看光线是不是平行的,如果光线是平行的,所得到的投影就是平行投影.四个选项中只有太阳光是平行光线,故太阳光线照射在物体上所形成的投影是平行投影.故选A.
7.④ 解析:根据从早晨到傍晚物体影子的指向是西-西北-北-东北-东,影长由长变短,再变长的规律可知时间顺序为③①④⑤②,中午时刻的影长为④.
8.解:如图所示,首先连接AE,过点C作AE的平行线;然后再过点D作BE的平行线,相交于点F,DF即为所求.
课后提升
1.A 解析:如图,过点B作BC⊥AA1,垂足为C.
∵A1B1是线段AB在投影面上的正投影,∴AA1⊥A1B1,BB1⊥A1B1.∴四边形A1B1BC为矩形.∴BC=A1B1.∠ACB=∠CBB1=90°,∴∠ABC=∠ABB1-∠CBB1=20°.∴BC=AB·cos 20°.∴A1B1=AB·cos 20°=a·cos 20°(cm).故选A.
2.A 解析:如图1,点O为光源,AB表示小明的手,CD表示小狗手影,则AB∥CD,过点O作OE⊥AB于点E,延长OE交CD于点F,则OF⊥CD.
图1
∵AB∥CD,∴△AOB∽△COD,则=.∵EF=1 m,OE=2 m,则OF=3 m.∴==.设AB=2k m,CD=3k m,∵在小明不动的情况下,要使小狗手影的高度增加一倍,如图2所示.
图2
∴AB=2k m,C'D'=6k m,E'F'=1 m,△AO'B∽△C'O'D'.∴==.则O'F'-O'E'=2O'E'=E'F'.∴O'E'= m.∴光源与小明的距离变化为OE-O'E'=2-=(m).故选A.
3.B 解析:如图,连接EF.根据题意,可得EF∥DB,故=.∴=.∴CF=2CE.设乙的速度为x,故甲的速度为2x,根据题意,甲所走的路程为BC→CE,即40+CE,乙所走的路程为BF,即40-CF,故可得=,解得CE=
8 m.故选B.
4.解:∵AB∥CD,AE∥CF,
∴∠ABE=∠CDF,∠AEB=∠CFD,
∴△ABE∽△CDF,
∴AB∶BE=CD∶DF.
∴AB∶7=2∶3,
解得AB=.
故树AB高 m.
5.解:(1)如图,圆锥的高DO=2 m,在Rt△DOB中,OB=BE+EO=4+2=6(m),
∴tan B===.
∴∠B=30°.
(2)如图,过点A作AF⊥BP,垂足为F.
∵∠B=30°,
∴∠ACP=2∠B=60°.
又∵∠ACP=∠B+∠BAC,
∴∠B=∠BAC.
∴AC=BC=BE+EC=8 m.
在Rt△ACF中,AF=AC·sin∠ACF=8·sin 60°=4(m).
故光源A到水平面的距离为4 m.
