32.3 直棱柱和圆锥的侧面展开图 课时作业(含答案) 2024-2025学年数学冀教版九年级下册
文档属性
| 名称 | 32.3 直棱柱和圆锥的侧面展开图 课时作业(含答案) 2024-2025学年数学冀教版九年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 299.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-26 00:00:00 | ||
图片预览

文档简介
32.3直棱柱和圆锥的侧面展开图
直棱柱的侧面展开图
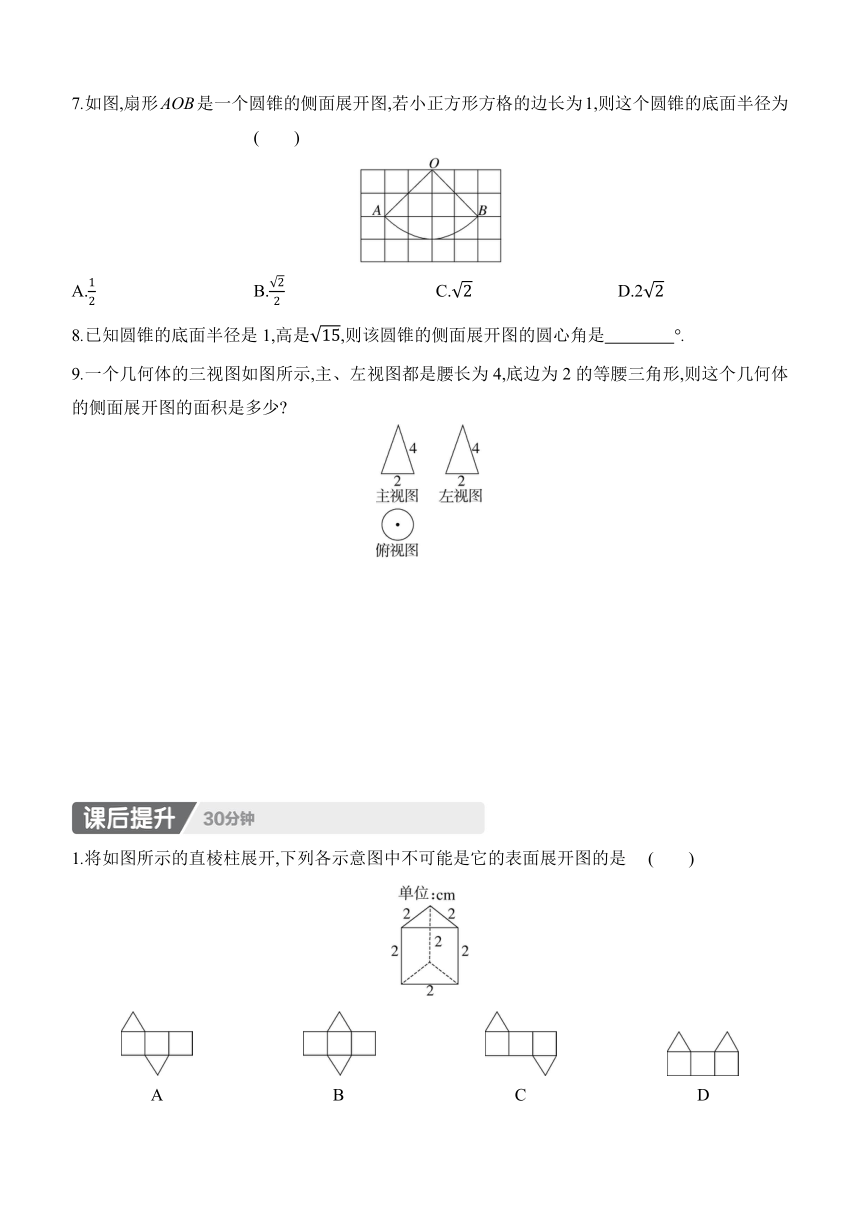
1.下列图形是四棱柱的侧面展开图的是 ( )
A B C D
2.如图是正方体的表面展开图,则与“话”字相对的字是 ( )
A.跟 B.党 C.走 D.听
3.如图,长方体的展开图不可能是 ( )
A B C D
4.若图1所示的正方体表面展开图是图2,则正方体上面的几何图形是 ( )
图1 图2
A B C D
锥体的侧面展开图
5.如图是一个几何体的侧面展开图,则该几何体是 ( )
A.三棱柱 B.三棱锥
C.五棱柱 D.五棱锥
6.一个圆锥的侧面展开图是半径为8的半圆,则该圆锥的表面积是 ( )
A.48π B.45π C.36π D.32π
7.如图,扇形AOB是一个圆锥的侧面展开图,若小正方形方格的边长为1,则这个圆锥的底面半径为 ( )
A. B. C. D.2
8.已知圆锥的底面半径是1,高是,则该圆锥的侧面展开图的圆心角是 °.
9.一个几何体的三视图如图所示,主、左视图都是腰长为4,底边为2的等腰三角形,则这个几何体的侧面展开图的面积是多少
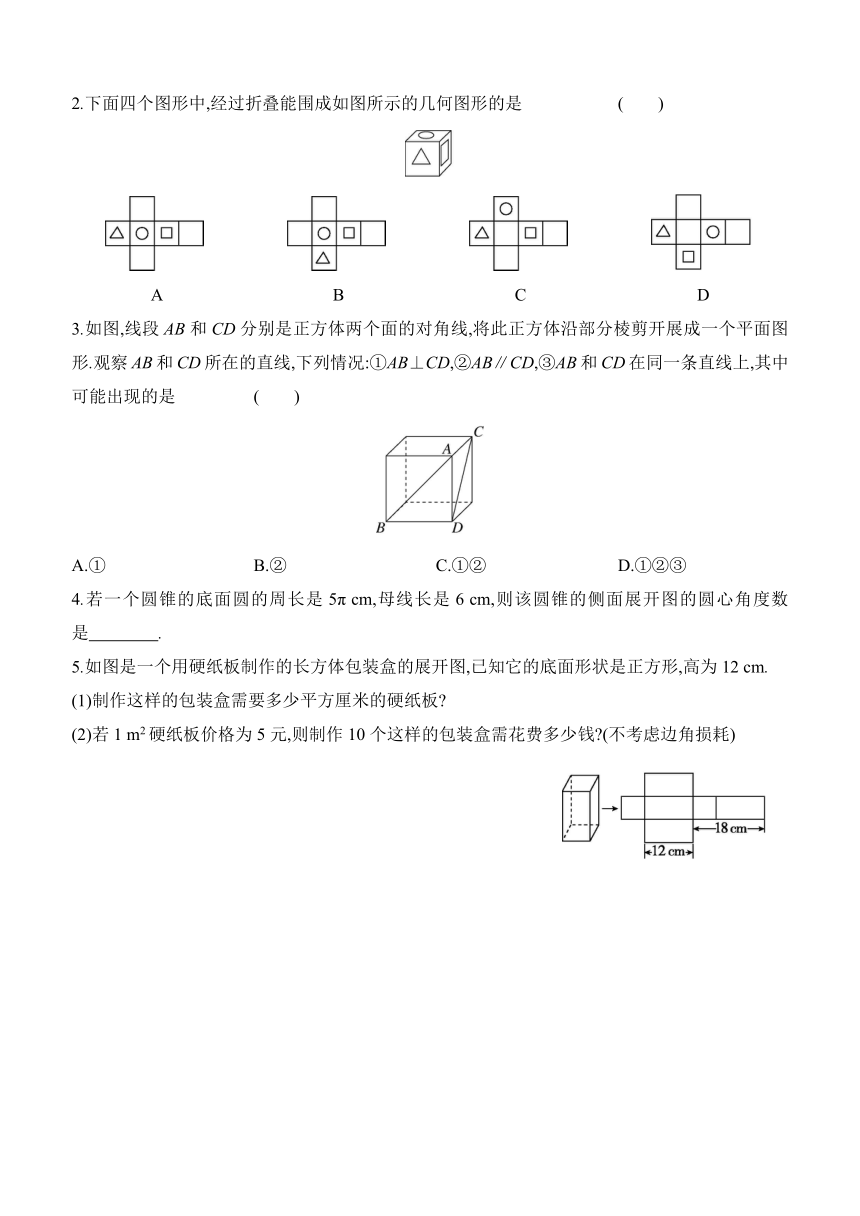
1.将如图所示的直棱柱展开,下列各示意图中不可能是它的表面展开图的是 ( )
A B C D
2.下面四个图形中,经过折叠能围成如图所示的几何图形的是 ( )
A B C D
3.如图,线段AB和CD分别是正方体两个面的对角线,将此正方体沿部分棱剪开展成一个平面图形.观察AB和CD所在的直线,下列情况:①AB⊥CD,②AB∥CD,③AB和CD在同一条直线上,其中可能出现的是 ( )
A.① B.② C.①② D.①②③
4.若一个圆锥的底面圆的周长是5π cm,母线长是6 cm,则该圆锥的侧面展开图的圆心角度数是 .
5.如图是一个用硬纸板制作的长方体包装盒的展开图,已知它的底面形状是正方形,高为12 cm.
(1)制作这样的包装盒需要多少平方厘米的硬纸板
(2)若1 m2硬纸板价格为5元,则制作10个这样的包装盒需花费多少钱 (不考虑边角损耗)
6.(空间观念)如图,圆柱形容器的高为1.2 m,底面圆周长为1 m,在容器内壁离容器底部0.3 m的点B处有一只蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3 m与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为多少米 (容器厚度忽略不计)
【详解答案】
课堂达标
1.A 解析:由四棱柱的特点,可知四棱柱的侧面展开图是四个小矩形组合成的大矩形.故选A.
2.C 解析:由正方体表面展开图,可知“话”与“走”是相对面.故选C.
3.D 解析:根据长方体的展开图,可知其表面展开图不正确的是D.故选D.
4.A 解析:由正方体的表面展开图及俯视图,可得三角形下面的边连着四个点的面,与四个点的面相对的是两个点的面,故正方体上面的是两个点的图.故选A.
5.D 解析:由题意,可知该几何体为五棱锥.故选D.
6.A 解析:设圆锥底面圆的半径为r,母线长为l,则l=8,底面圆的周长等于半圆的弧长8π,∴2πr=8π.∴r=4.∴圆锥的表面积=S侧+S底=πrl+πr2=32π+16π=48π.故选A.
7.B 解析:的长==π,设圆锥底面圆的半径为r,则有2πr=π,∴r=.故选B.
8.90 解析:设圆锥的母线长为a,根据勾股定理,得a=4.设圆锥的侧面展开图的圆心角度数为n°,根据题意,得2π×1=,解得n=90,即圆锥的侧面展开图的圆心角度数为90°.
9.解:依题意,知母线长l=4,底面半径r=1,则由圆锥的侧面积公式,得S=πrl=π×1×4=4π.
课后提升
1.D 解析:选项A、B、C均可能是该直棱柱的表面展开图,而选项D中的两个底面会重叠,不可能是它的表面展开图.故选D.
2.B 解析:三角形图案所在的面应与正方形图案所在的面相邻,而选项A、C与此不符;三角形图案所在的面应与圆形图案所在的面相邻,而选项D与此不符.正确的是B.故选B.
3.C 解析:①如图1,AB⊥CD.
图1
②如图2,AB∥CD.
图2
③无论通过什么方式展开,AB,CD都不可能在同一条直线上.故选C.
4.150° 解析:设圆锥侧面展开图的圆心角为n°.∵圆锥的底面圆的周长是5π cm,∴圆锥的侧面展开图(扇形)的弧长为5π cm.∴=5π,解得n=150.
5.解:(1)由题意,得底面正方形的边长=18-12=6(cm),则包装盒表面积=2×(12×6+12×6+6×6)=360(cm2).
答:制作这样的包装盒需要360 cm2的硬纸板.
(2)360÷10 000×5×10=1.8(元).
答:制作10个这样的包装盒需花费1.8元钱.
6.解:如图,将容器侧面展开,作点A关于EE'的对称点A',连接A'B,则A'B即为最短距离.由题意,得A'D=0.5 m,DG=A'E=AE=BC=0.3 m,CG=1.2 m,∴BD=CG+DG-BC=1.2+0.3-0.3=1.2(m),
则A'B===1.3(m).
直棱柱的侧面展开图
1.下列图形是四棱柱的侧面展开图的是 ( )
A B C D
2.如图是正方体的表面展开图,则与“话”字相对的字是 ( )
A.跟 B.党 C.走 D.听
3.如图,长方体的展开图不可能是 ( )
A B C D
4.若图1所示的正方体表面展开图是图2,则正方体上面的几何图形是 ( )
图1 图2
A B C D
锥体的侧面展开图
5.如图是一个几何体的侧面展开图,则该几何体是 ( )
A.三棱柱 B.三棱锥
C.五棱柱 D.五棱锥
6.一个圆锥的侧面展开图是半径为8的半圆,则该圆锥的表面积是 ( )
A.48π B.45π C.36π D.32π
7.如图,扇形AOB是一个圆锥的侧面展开图,若小正方形方格的边长为1,则这个圆锥的底面半径为 ( )
A. B. C. D.2
8.已知圆锥的底面半径是1,高是,则该圆锥的侧面展开图的圆心角是 °.
9.一个几何体的三视图如图所示,主、左视图都是腰长为4,底边为2的等腰三角形,则这个几何体的侧面展开图的面积是多少
1.将如图所示的直棱柱展开,下列各示意图中不可能是它的表面展开图的是 ( )
A B C D
2.下面四个图形中,经过折叠能围成如图所示的几何图形的是 ( )
A B C D
3.如图,线段AB和CD分别是正方体两个面的对角线,将此正方体沿部分棱剪开展成一个平面图形.观察AB和CD所在的直线,下列情况:①AB⊥CD,②AB∥CD,③AB和CD在同一条直线上,其中可能出现的是 ( )
A.① B.② C.①② D.①②③
4.若一个圆锥的底面圆的周长是5π cm,母线长是6 cm,则该圆锥的侧面展开图的圆心角度数是 .
5.如图是一个用硬纸板制作的长方体包装盒的展开图,已知它的底面形状是正方形,高为12 cm.
(1)制作这样的包装盒需要多少平方厘米的硬纸板
(2)若1 m2硬纸板价格为5元,则制作10个这样的包装盒需花费多少钱 (不考虑边角损耗)
6.(空间观念)如图,圆柱形容器的高为1.2 m,底面圆周长为1 m,在容器内壁离容器底部0.3 m的点B处有一只蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3 m与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为多少米 (容器厚度忽略不计)
【详解答案】
课堂达标
1.A 解析:由四棱柱的特点,可知四棱柱的侧面展开图是四个小矩形组合成的大矩形.故选A.
2.C 解析:由正方体表面展开图,可知“话”与“走”是相对面.故选C.
3.D 解析:根据长方体的展开图,可知其表面展开图不正确的是D.故选D.
4.A 解析:由正方体的表面展开图及俯视图,可得三角形下面的边连着四个点的面,与四个点的面相对的是两个点的面,故正方体上面的是两个点的图.故选A.
5.D 解析:由题意,可知该几何体为五棱锥.故选D.
6.A 解析:设圆锥底面圆的半径为r,母线长为l,则l=8,底面圆的周长等于半圆的弧长8π,∴2πr=8π.∴r=4.∴圆锥的表面积=S侧+S底=πrl+πr2=32π+16π=48π.故选A.
7.B 解析:的长==π,设圆锥底面圆的半径为r,则有2πr=π,∴r=.故选B.
8.90 解析:设圆锥的母线长为a,根据勾股定理,得a=4.设圆锥的侧面展开图的圆心角度数为n°,根据题意,得2π×1=,解得n=90,即圆锥的侧面展开图的圆心角度数为90°.
9.解:依题意,知母线长l=4,底面半径r=1,则由圆锥的侧面积公式,得S=πrl=π×1×4=4π.
课后提升
1.D 解析:选项A、B、C均可能是该直棱柱的表面展开图,而选项D中的两个底面会重叠,不可能是它的表面展开图.故选D.
2.B 解析:三角形图案所在的面应与正方形图案所在的面相邻,而选项A、C与此不符;三角形图案所在的面应与圆形图案所在的面相邻,而选项D与此不符.正确的是B.故选B.
3.C 解析:①如图1,AB⊥CD.
图1
②如图2,AB∥CD.
图2
③无论通过什么方式展开,AB,CD都不可能在同一条直线上.故选C.
4.150° 解析:设圆锥侧面展开图的圆心角为n°.∵圆锥的底面圆的周长是5π cm,∴圆锥的侧面展开图(扇形)的弧长为5π cm.∴=5π,解得n=150.
5.解:(1)由题意,得底面正方形的边长=18-12=6(cm),则包装盒表面积=2×(12×6+12×6+6×6)=360(cm2).
答:制作这样的包装盒需要360 cm2的硬纸板.
(2)360÷10 000×5×10=1.8(元).
答:制作10个这样的包装盒需花费1.8元钱.
6.解:如图,将容器侧面展开,作点A关于EE'的对称点A',连接A'B,则A'B即为最短距离.由题意,得A'D=0.5 m,DG=A'E=AE=BC=0.3 m,CG=1.2 m,∴BD=CG+DG-BC=1.2+0.3-0.3=1.2(m),
则A'B===1.3(m).
