第三十二章 投影与视图 单元评估测试卷 (含答案) 2024-2025学年数学冀教版九年级下册
文档属性
| 名称 | 第三十二章 投影与视图 单元评估测试卷 (含答案) 2024-2025学年数学冀教版九年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 315.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-26 00:00:00 | ||
图片预览



文档简介
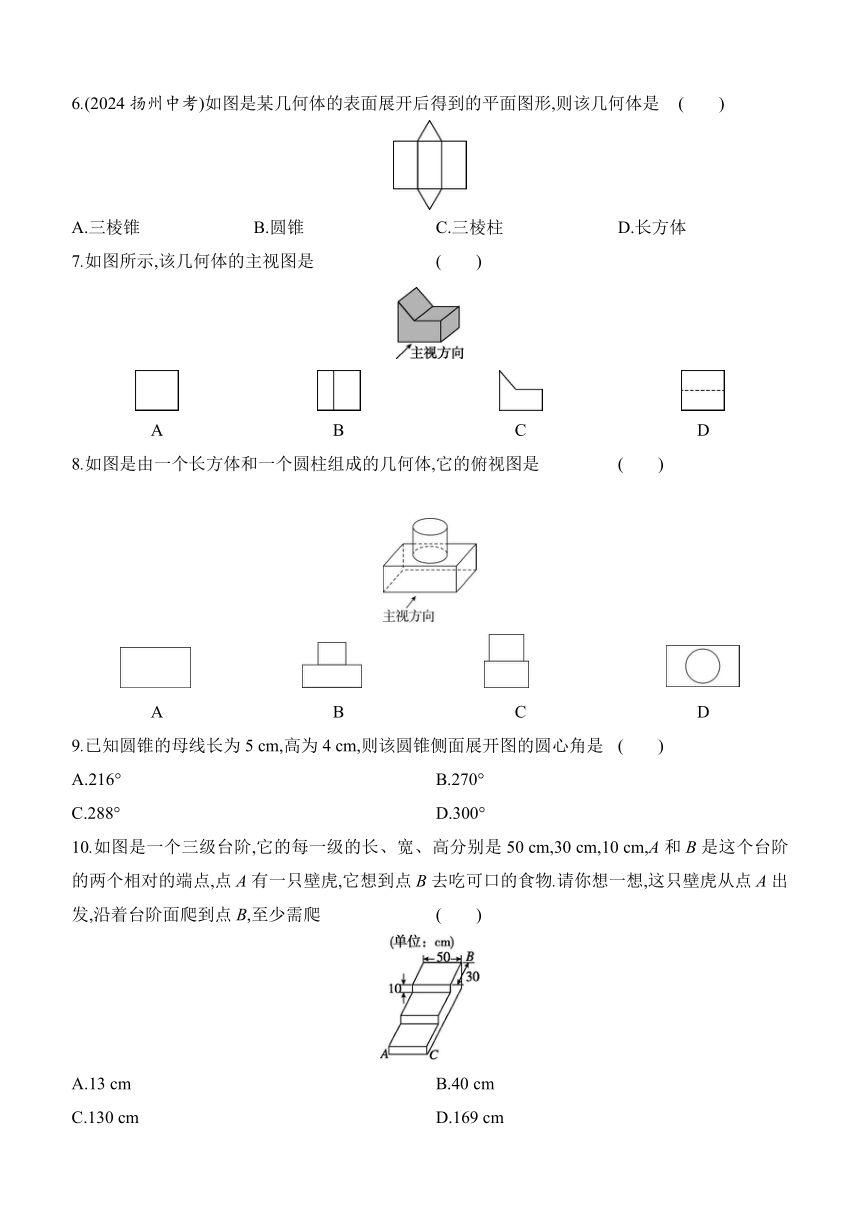
第三十二章 投影与视图 评估测试卷
(满分:120分 时间:120分钟)
一、选择题(本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列生活现象不是利用投影的是 ( )
A.放电影 B.照相
C.树影 D.皮影
2.如图,在一间黑屋子里用一盏白炽灯照一个球,球在地面上的阴影的形状是一个圆,当把白炽灯向上远移时,圆形阴影的大小的变化情况是 ( )
A.越来越小 B.越来越大
C.大小不变 D.不能确定
3.下列几何体的主视图是圆的是 ( )
A B C D
4.(2024广安中考)将“共建平安校园”六个汉字分别写在某正方体的表面上.如图是它的一种展开图,则在原正方体上,与“共”字所在面相对的面上的汉字是 ( )
A.校 B.安 C.平 D.园
5.(2024安徽中考)某几何体的三视图如图所示,则该几何体为 ( )
A B C D
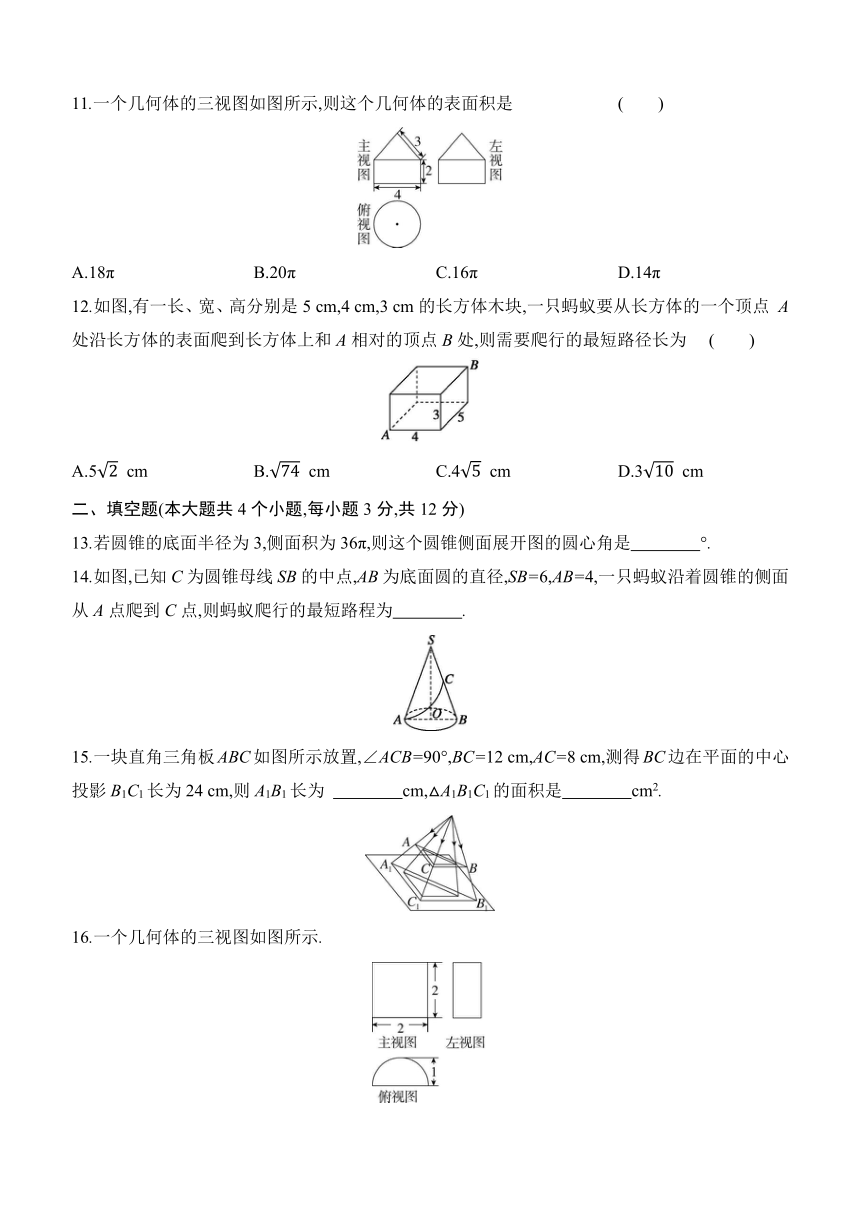
6.(2024扬州中考)如图是某几何体的表面展开后得到的平面图形,则该几何体是 ( )
A.三棱锥 B.圆锥 C.三棱柱 D.长方体
7.如图所示,该几何体的主视图是 ( )
A B C D
8.如图是由一个长方体和一个圆柱组成的几何体,它的俯视图是 ( )
A B C D
9.已知圆锥的母线长为5 cm,高为4 cm,则该圆锥侧面展开图的圆心角是 ( )
A.216° B.270°
C.288° D.300°
10.如图是一个三级台阶,它的每一级的长、宽、高分别是50 cm,30 cm,10 cm,A和B是这个台阶的两个相对的端点,点A有一只壁虎,它想到点B去吃可口的食物.请你想一想,这只壁虎从点A出发,沿着台阶面爬到点B,至少需爬 ( )
A.13 cm B.40 cm
C.130 cm D.169 cm
11.一个几何体的三视图如图所示,则这个几何体的表面积是 ( )
A.18π B.20π C.16π D.14π
12.如图,有一长、宽、高分别是5 cm,4 cm,3 cm的长方体木块,一只蚂蚁要从长方体的一个顶点 A处沿长方体的表面爬到长方体上和A相对的顶点B处,则需要爬行的最短路径长为 ( )
A.5 cm B. cm C.4 cm D.3 cm
二、填空题(本大题共4个小题,每小题3分,共12分)
13.若圆锥的底面半径为3,侧面积为36π,则这个圆锥侧面展开图的圆心角是 °.
14.如图,已知C为圆锥母线SB的中点,AB为底面圆的直径,SB=6,AB=4,一只蚂蚁沿着圆锥的侧面从A点爬到C点,则蚂蚁爬行的最短路程为 .
15.一块直角三角板ABC如图所示放置,∠ACB=90°,BC=12 cm,AC=8 cm,测得BC边在平面的中心投影B1C1长为24 cm,则A1B1长为 cm,△A1B1C1的面积是 cm2.
16.一个几何体的三视图如图所示.
(1)该几何体为 .
(2)该几何体的表面积为 ,体积为 .
三、解答题(本大题共8个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
17.(6分)某数学活动小组利用太阳光线下物体的影子和标杆测量旗杆的高度.如图,在某一时刻,旗杆AB的影子为BC,与此同时在C处立一根标杆CD,标杆CD的影子为CE,CD=1.8 m,BC=5CD.
(1)求BC的长.
(2)从条件①、条件②这两个条件中选择一个作为已知,求旗杆AB的高度.
条件①:CE=1.2 m;条件②:从D处看旗杆顶部A的仰角α为52.46°.
注:如果选择条件①和条件②分别作答,按第一个解答计分.参考数据:sin 52.46°≈0.79,cos 52.46°≈0.61,tan 52.46°≈1.30.
18.(8分)如图所示的是某个几何体的三视图.
(1)说出这个几何体的名称.
(2)根据图中有关数据,求这个几何体的表面积.
19.(8分)数学实践小组的同学利用太阳光下形成的影子测量大树的高度.在同一时刻,他们测得身高为1.5 m的同学立正站立时的影长为2 m,大树的影子分别落在水平地面和台阶上.已知大树在地面的影长BC为2.4 m,台阶的高度均为0.3 m,宽度均为0.5 m.求大树的高度AB.
20.(8分)已知图1为一个正方体,其棱长为12,图2为图1的表面展开图(数字和字母写在外面),请根据要求回答问题:
图1 图2
(1)若正方体相对面上的数互为相反数,则xy= .
(2)用一个平面去截这个正方体,下列关于截面(截出的面)的形状的结论:①可能是锐角三角形;②可能是直角三角形;③可能是钝角三角形;④可能是平行四边形.其中所有正确结论的序号是( )
A.①② B.①④ C.①②④ D.①②③④
(3)图1中,M,N为所在棱的中点,请在图2标出点M的位置,并求出展开图中△ABM的面积.
21.(9分)如图是一张铁皮.
(1)计算该铁皮的面积.
(2)它能否做成一个长方体盒子 若能,画出它的几何图形,并计算它的体积;若不能,说明理由.
22.(10分)如图,某学校旗杆AB旁边有一个半圆的时钟模型.时钟的9点和3点的刻度线刚好和地面重合,半圆的半径为2 m,旗杆的底端A到钟面9点刻度C的距离为11 m.一天,小明观察到阳光下旗杆顶端B的影子刚好投到时钟的11点的刻度上,同时测得1 m长的标杆的影长为1.2 m,求旗杆AB的高度.
23.(11分)(2024广东中考)综合与实践
【主题】滤纸与漏斗
【素材】如图①所示:
①一张直径为10 cm的圆形滤纸;
②一只漏斗口直径与母线均为7 cm的圆锥形过滤漏斗.
图①
【实践操作】
步骤1:取一张滤纸;
步骤2:按如图②所示步骤折叠好滤纸;
步骤3:将其中一层撑开,围成圆锥形;
步骤4:将围成圆锥形的滤纸放入如图1所示漏斗中.
图②
【实践探索】
(1)滤纸是否能紧贴此漏斗内壁(忽略漏斗管口处) 用你所学的数学知识说明.
(2)当滤纸紧贴漏斗内壁时,求滤纸围成的圆锥形的体积.(结果保留π)
24.(12分)(2024自贡中考)为测量水平操场上旗杆的高度,九(2)班各学习小组运用了多种测量方法.
图①(利用影子) 图②(利用镜子) 图③(利用标杆)
(1)如图①,小张在测量时发现,自己在操场上的影长EF恰好等于自己的身高DE.此时,小组同学测得旗杆AB的影长BC为11.3 m,据此可得旗杆高度为 m.
(2)如图②,小李站在操场上E点处,前面水平放置镜面C,并通过镜面观测到旗杆顶部A.小组同学测得小李的眼睛距地面高度DE=1.5 m,小李到镜面距离EC=2 m,镜面到旗杆的距离CB=16 m.求旗杆高度.
(3)小王所在小组采用图③的方法测量,结果误差较大.在更新测量工具,优化测量方法后,测量精度明显提高.研学旅行时,他们利用自制工具,成功测量了江姐故里广场雕塑的高度.方法如下:
图④(找水平线) 图⑤(找定标高线) 图⑥(测雕塑高)
如图④,在透明的塑料软管内注入适量的水,利用连通器原理,保持管内水面M,N两点始终处于同一水平线上.
如图⑤,在支架上端P处,用细线系小重物Q,标高线PQ始终垂直于水平地面.
如图⑥,在江姐故里广场上E点处,同学们用注水管确定与雕塑底部B处于同一水平线的D,G两点,并标记观测视线DA与标高线交点C,测得标高CG=1.8 m,DG=1.5 m.将观测点D后移24 m到D'处,采用同样方法,测得C'G'=1.2 m,D'G'=2 m.求雕塑高度(结果精确到1 m).
【详解答案】
1.B 解析:根据投影的概念,放电影、树影、皮影都是由光线照射形成的,都是投影,而照相不满足,不是投影.故选B.
2.A 解析:当点光源在物体上方,向下照射物体时,点光源离物体越近,影子越大;点光源离物体越远,影子越小.故圆形阴影越来越小.故选A.
3.A 解析:A.主视图为圆,符合题意;B.主视图为正方形,不符合题意;C.主视图为三角形,不符合题意;D.主视图为并排的两个矩形,不符合题意.故选A.
4.A 解析:与“共”字所在面相对的面上的汉字是“校”.故选A.
5.D 解析:根据题图,结合三视图的定义以及几何体的形状特征可得该几何体为D选项.故选D.
6.C 解析:根据题图,上、下是两个三角形,中间是长方形.∴该几何体是三棱柱.故选C.
7.C 解析:从正面看得到的图形是.故选C.
8.D
9.A 解析:设该圆锥侧面展开图的圆心角为n°.由题意,可得圆锥的底面圆的半径==3.根据题意,得2π×3=,解得n=216,即该圆锥侧面展开图的圆心角为216°.故选A.
10.C 解析:将台阶面展开,连接AB,如图,线段AB即为壁虎所爬的最短路线.
∵BC=30×3+10×3=120(cm),AC=50 cm,
∴在Rt△ABC中,根据勾股定理,得AB==130 cm.∴壁虎至少需爬130 cm.
11.A 解析:依题意,知这个几何体是圆锥和圆柱的组合体,圆锥的底面半径=4÷2=2,母线长为3,圆柱的底面半径=4÷2=2,高为2,则这个几何体的表面积是π×2×3+π×22+π×2×2×2=6π+4π+8π=18π.故选A.
12.B 解析:从长方体的一个顶点A出发,沿表面爬到另一个顶点B处,有三种方案,如图是它们的三种侧面展开图.如图1,由勾股定理,得AB===4(cm);如图2,由勾股定理,得AB===3(cm);如图3,由勾股定理,得AB==(cm).∵<<,∴蚂蚁从顶点A爬到相对的顶点B处需要爬行的最短路径长为 cm.故选B.
图1 图2 图3
13.90 解析:根据圆锥侧面积公式:S=πrl,可得π×3×l=36π.解得l=12.∴=36π.解得n=90.∴侧面展开图的圆心角是90°.
14.3 解析:展开圆锥侧面并连接AB,如图所示.
∵题图中AB为底面圆的直径,且AB=4,∴底面圆周长为4π.设圆锥的侧面展开图的圆心角为n°,∵圆锥母线SB=6,根据底面圆周长等于展开后扇形的弧长可得4π=,解得n=120.∴∠ASC=60°.∵半径SA=SB,∴△SAB是等边三角形.∵C为圆锥母线SB的中点.∴AC⊥SB.在Rt△ACS中,AC=SA·sin 60°=6×=3.∴蚂蚁爬行的最短路程为3.
15.8 192 解析:∵∠ACB=90°,BC=12 cm,AC=8 cm,∴AB=4 cm.
∵△ABC∽△A1B1C1,∴A1B1∶AB=B1C1∶BC=A1C1∶AC=2∶1.
∴A1B1=8 cm,A1C1=16 cm.∵∠A1C1B1=∠ACB=90°,
∴=·A1C1·B1C1=×16×24=192(cm2).
16.(1)半个圆柱 (2)3π+4 π
解析:(1)根据三视图知该几何体为半个圆柱.(2)该几何体的底面圆的半径为1,高为2,所以该几何体的表面积为π×12+2×2+×2π×1×2=3π+4,体积为×π×12×2=π.
17.解:(1)∵BC=5CD,
CD=1.8 m,
∴BC=5×1.8=9(m).
∴BC的长为9 m.
(2)若选择条件①:
由同一时刻物高与影长成正比,得=.
∴=.
∴AB=13.5(m).
∴旗杆AB的高度为13.5 m.
若选择条件②:
过点D作DF⊥AB,垂足为F,
则DC=BF=1.8 m,DF=BC=9 m.
在Rt△ADF中,∠ADF=52.46°.
∴AF=DF·tan 52.46°≈9×1.3=11.7(m).
∴AB=AF+BF=11.7+1.8=13.5(m).
∴旗杆AB的高度约为13.5 m.
18.解:(1)根据三视图,可得这个几何体是三棱柱.
(2)表面积为×3×4×2+15×3+15×4+15×5=192.
19.解:如图,延长DH交BC的延长线于点M,延长AD交BC的延长线于点N.
可求得BM=3.4 m,DM=0.9 m.
由=,
可得MN=1.2(m).
所以BN=3.4+1.2=4.6(m).
由=,
可得AB=3.45(m).
所以大树的高度AB为3.45 m.
20.解:(1)-12 (2)B
(3)如图,
=×12×6=36,
=×12×30=180.
所以S△ABM的面积为36或180.
21.解:(1)根据图中尺寸计算铁皮的面积为(1×3)×2+(2×3)×2+(1×2)×2=22(m2).
(2)能做成一个长方体盒子,如图.其体积为3×1×2=6(m3).
22.解:如图,过点D作DE⊥AC于点E,作DF⊥AB于点F.设半圆圆心为O,连接OD.
∵点D在11点的刻度上,
∴∠COD=60°.
∴DE=OD·sin 60°=2×=(m),OE=OD·cos 60°=2×=1(m).
∴CE=2-1=1(m).
∵BA⊥AE,DE⊥AE,BA⊥DF,
∴∠FAE=∠AED=∠DFA=90°.
∴四边形AEDF为矩形.
∴DF=AE=11+1=12(m),AF=DE= m.
∵同时测得1 m长的标杆的影长为1.2 m,
∴=.∴BF=10(m).
∴AB=BF+FA=(10+)m.
答:旗杆AB的高度为(10+)m.
23.解:(1)能,理由:设圆锥侧面展开图(扇形)的圆心角为n°.
根据题意,得=7π,
解得n=180.
∴将圆形滤纸对折,将其中一层撑开,围成圆锥形,此时滤纸能紧贴此漏斗内壁.
(2)设滤纸围成的圆锥形底面圆的半径为r cm,高为h cm,
根据题意,
得2πr=,解得r=.
∴h==.
∴所求圆锥的体积为πr2h=π× = (cm3).
24.解:(1)11.3
(2)由题意,得DE=1.5 m,EC=2 m,BC=16 m.
根据镜面反射可知,∠ACB=∠ECD.
∵AB⊥BE,DE⊥BE,
∴∠ABC=∠DEC=90°.
∴△ACB∽△DCE.
∴=,
即=.
∴AB=12(m).
答:旗杆高度为12 m.
(3)设BG=x m,
由题意,得△DGC∽△DBA,△D'G'C'∽△D'BA.
∴=,=.
即=,=.
∴=.
整理得3.6=1.8,
解得x=22.5.经检验x=22.5是原方程的解且符合题意.
∴AB=1.8×÷1.5=28.8≈29(m).
答:雕塑高度约为29 m.
(满分:120分 时间:120分钟)
一、选择题(本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列生活现象不是利用投影的是 ( )
A.放电影 B.照相
C.树影 D.皮影
2.如图,在一间黑屋子里用一盏白炽灯照一个球,球在地面上的阴影的形状是一个圆,当把白炽灯向上远移时,圆形阴影的大小的变化情况是 ( )
A.越来越小 B.越来越大
C.大小不变 D.不能确定
3.下列几何体的主视图是圆的是 ( )
A B C D
4.(2024广安中考)将“共建平安校园”六个汉字分别写在某正方体的表面上.如图是它的一种展开图,则在原正方体上,与“共”字所在面相对的面上的汉字是 ( )
A.校 B.安 C.平 D.园
5.(2024安徽中考)某几何体的三视图如图所示,则该几何体为 ( )
A B C D
6.(2024扬州中考)如图是某几何体的表面展开后得到的平面图形,则该几何体是 ( )
A.三棱锥 B.圆锥 C.三棱柱 D.长方体
7.如图所示,该几何体的主视图是 ( )
A B C D
8.如图是由一个长方体和一个圆柱组成的几何体,它的俯视图是 ( )
A B C D
9.已知圆锥的母线长为5 cm,高为4 cm,则该圆锥侧面展开图的圆心角是 ( )
A.216° B.270°
C.288° D.300°
10.如图是一个三级台阶,它的每一级的长、宽、高分别是50 cm,30 cm,10 cm,A和B是这个台阶的两个相对的端点,点A有一只壁虎,它想到点B去吃可口的食物.请你想一想,这只壁虎从点A出发,沿着台阶面爬到点B,至少需爬 ( )
A.13 cm B.40 cm
C.130 cm D.169 cm
11.一个几何体的三视图如图所示,则这个几何体的表面积是 ( )
A.18π B.20π C.16π D.14π
12.如图,有一长、宽、高分别是5 cm,4 cm,3 cm的长方体木块,一只蚂蚁要从长方体的一个顶点 A处沿长方体的表面爬到长方体上和A相对的顶点B处,则需要爬行的最短路径长为 ( )
A.5 cm B. cm C.4 cm D.3 cm
二、填空题(本大题共4个小题,每小题3分,共12分)
13.若圆锥的底面半径为3,侧面积为36π,则这个圆锥侧面展开图的圆心角是 °.
14.如图,已知C为圆锥母线SB的中点,AB为底面圆的直径,SB=6,AB=4,一只蚂蚁沿着圆锥的侧面从A点爬到C点,则蚂蚁爬行的最短路程为 .
15.一块直角三角板ABC如图所示放置,∠ACB=90°,BC=12 cm,AC=8 cm,测得BC边在平面的中心投影B1C1长为24 cm,则A1B1长为 cm,△A1B1C1的面积是 cm2.
16.一个几何体的三视图如图所示.
(1)该几何体为 .
(2)该几何体的表面积为 ,体积为 .
三、解答题(本大题共8个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
17.(6分)某数学活动小组利用太阳光线下物体的影子和标杆测量旗杆的高度.如图,在某一时刻,旗杆AB的影子为BC,与此同时在C处立一根标杆CD,标杆CD的影子为CE,CD=1.8 m,BC=5CD.
(1)求BC的长.
(2)从条件①、条件②这两个条件中选择一个作为已知,求旗杆AB的高度.
条件①:CE=1.2 m;条件②:从D处看旗杆顶部A的仰角α为52.46°.
注:如果选择条件①和条件②分别作答,按第一个解答计分.参考数据:sin 52.46°≈0.79,cos 52.46°≈0.61,tan 52.46°≈1.30.
18.(8分)如图所示的是某个几何体的三视图.
(1)说出这个几何体的名称.
(2)根据图中有关数据,求这个几何体的表面积.
19.(8分)数学实践小组的同学利用太阳光下形成的影子测量大树的高度.在同一时刻,他们测得身高为1.5 m的同学立正站立时的影长为2 m,大树的影子分别落在水平地面和台阶上.已知大树在地面的影长BC为2.4 m,台阶的高度均为0.3 m,宽度均为0.5 m.求大树的高度AB.
20.(8分)已知图1为一个正方体,其棱长为12,图2为图1的表面展开图(数字和字母写在外面),请根据要求回答问题:
图1 图2
(1)若正方体相对面上的数互为相反数,则xy= .
(2)用一个平面去截这个正方体,下列关于截面(截出的面)的形状的结论:①可能是锐角三角形;②可能是直角三角形;③可能是钝角三角形;④可能是平行四边形.其中所有正确结论的序号是( )
A.①② B.①④ C.①②④ D.①②③④
(3)图1中,M,N为所在棱的中点,请在图2标出点M的位置,并求出展开图中△ABM的面积.
21.(9分)如图是一张铁皮.
(1)计算该铁皮的面积.
(2)它能否做成一个长方体盒子 若能,画出它的几何图形,并计算它的体积;若不能,说明理由.
22.(10分)如图,某学校旗杆AB旁边有一个半圆的时钟模型.时钟的9点和3点的刻度线刚好和地面重合,半圆的半径为2 m,旗杆的底端A到钟面9点刻度C的距离为11 m.一天,小明观察到阳光下旗杆顶端B的影子刚好投到时钟的11点的刻度上,同时测得1 m长的标杆的影长为1.2 m,求旗杆AB的高度.
23.(11分)(2024广东中考)综合与实践
【主题】滤纸与漏斗
【素材】如图①所示:
①一张直径为10 cm的圆形滤纸;
②一只漏斗口直径与母线均为7 cm的圆锥形过滤漏斗.
图①
【实践操作】
步骤1:取一张滤纸;
步骤2:按如图②所示步骤折叠好滤纸;
步骤3:将其中一层撑开,围成圆锥形;
步骤4:将围成圆锥形的滤纸放入如图1所示漏斗中.
图②
【实践探索】
(1)滤纸是否能紧贴此漏斗内壁(忽略漏斗管口处) 用你所学的数学知识说明.
(2)当滤纸紧贴漏斗内壁时,求滤纸围成的圆锥形的体积.(结果保留π)
24.(12分)(2024自贡中考)为测量水平操场上旗杆的高度,九(2)班各学习小组运用了多种测量方法.
图①(利用影子) 图②(利用镜子) 图③(利用标杆)
(1)如图①,小张在测量时发现,自己在操场上的影长EF恰好等于自己的身高DE.此时,小组同学测得旗杆AB的影长BC为11.3 m,据此可得旗杆高度为 m.
(2)如图②,小李站在操场上E点处,前面水平放置镜面C,并通过镜面观测到旗杆顶部A.小组同学测得小李的眼睛距地面高度DE=1.5 m,小李到镜面距离EC=2 m,镜面到旗杆的距离CB=16 m.求旗杆高度.
(3)小王所在小组采用图③的方法测量,结果误差较大.在更新测量工具,优化测量方法后,测量精度明显提高.研学旅行时,他们利用自制工具,成功测量了江姐故里广场雕塑的高度.方法如下:
图④(找水平线) 图⑤(找定标高线) 图⑥(测雕塑高)
如图④,在透明的塑料软管内注入适量的水,利用连通器原理,保持管内水面M,N两点始终处于同一水平线上.
如图⑤,在支架上端P处,用细线系小重物Q,标高线PQ始终垂直于水平地面.
如图⑥,在江姐故里广场上E点处,同学们用注水管确定与雕塑底部B处于同一水平线的D,G两点,并标记观测视线DA与标高线交点C,测得标高CG=1.8 m,DG=1.5 m.将观测点D后移24 m到D'处,采用同样方法,测得C'G'=1.2 m,D'G'=2 m.求雕塑高度(结果精确到1 m).
【详解答案】
1.B 解析:根据投影的概念,放电影、树影、皮影都是由光线照射形成的,都是投影,而照相不满足,不是投影.故选B.
2.A 解析:当点光源在物体上方,向下照射物体时,点光源离物体越近,影子越大;点光源离物体越远,影子越小.故圆形阴影越来越小.故选A.
3.A 解析:A.主视图为圆,符合题意;B.主视图为正方形,不符合题意;C.主视图为三角形,不符合题意;D.主视图为并排的两个矩形,不符合题意.故选A.
4.A 解析:与“共”字所在面相对的面上的汉字是“校”.故选A.
5.D 解析:根据题图,结合三视图的定义以及几何体的形状特征可得该几何体为D选项.故选D.
6.C 解析:根据题图,上、下是两个三角形,中间是长方形.∴该几何体是三棱柱.故选C.
7.C 解析:从正面看得到的图形是.故选C.
8.D
9.A 解析:设该圆锥侧面展开图的圆心角为n°.由题意,可得圆锥的底面圆的半径==3.根据题意,得2π×3=,解得n=216,即该圆锥侧面展开图的圆心角为216°.故选A.
10.C 解析:将台阶面展开,连接AB,如图,线段AB即为壁虎所爬的最短路线.
∵BC=30×3+10×3=120(cm),AC=50 cm,
∴在Rt△ABC中,根据勾股定理,得AB==130 cm.∴壁虎至少需爬130 cm.
11.A 解析:依题意,知这个几何体是圆锥和圆柱的组合体,圆锥的底面半径=4÷2=2,母线长为3,圆柱的底面半径=4÷2=2,高为2,则这个几何体的表面积是π×2×3+π×22+π×2×2×2=6π+4π+8π=18π.故选A.
12.B 解析:从长方体的一个顶点A出发,沿表面爬到另一个顶点B处,有三种方案,如图是它们的三种侧面展开图.如图1,由勾股定理,得AB===4(cm);如图2,由勾股定理,得AB===3(cm);如图3,由勾股定理,得AB==(cm).∵<<,∴蚂蚁从顶点A爬到相对的顶点B处需要爬行的最短路径长为 cm.故选B.
图1 图2 图3
13.90 解析:根据圆锥侧面积公式:S=πrl,可得π×3×l=36π.解得l=12.∴=36π.解得n=90.∴侧面展开图的圆心角是90°.
14.3 解析:展开圆锥侧面并连接AB,如图所示.
∵题图中AB为底面圆的直径,且AB=4,∴底面圆周长为4π.设圆锥的侧面展开图的圆心角为n°,∵圆锥母线SB=6,根据底面圆周长等于展开后扇形的弧长可得4π=,解得n=120.∴∠ASC=60°.∵半径SA=SB,∴△SAB是等边三角形.∵C为圆锥母线SB的中点.∴AC⊥SB.在Rt△ACS中,AC=SA·sin 60°=6×=3.∴蚂蚁爬行的最短路程为3.
15.8 192 解析:∵∠ACB=90°,BC=12 cm,AC=8 cm,∴AB=4 cm.
∵△ABC∽△A1B1C1,∴A1B1∶AB=B1C1∶BC=A1C1∶AC=2∶1.
∴A1B1=8 cm,A1C1=16 cm.∵∠A1C1B1=∠ACB=90°,
∴=·A1C1·B1C1=×16×24=192(cm2).
16.(1)半个圆柱 (2)3π+4 π
解析:(1)根据三视图知该几何体为半个圆柱.(2)该几何体的底面圆的半径为1,高为2,所以该几何体的表面积为π×12+2×2+×2π×1×2=3π+4,体积为×π×12×2=π.
17.解:(1)∵BC=5CD,
CD=1.8 m,
∴BC=5×1.8=9(m).
∴BC的长为9 m.
(2)若选择条件①:
由同一时刻物高与影长成正比,得=.
∴=.
∴AB=13.5(m).
∴旗杆AB的高度为13.5 m.
若选择条件②:
过点D作DF⊥AB,垂足为F,
则DC=BF=1.8 m,DF=BC=9 m.
在Rt△ADF中,∠ADF=52.46°.
∴AF=DF·tan 52.46°≈9×1.3=11.7(m).
∴AB=AF+BF=11.7+1.8=13.5(m).
∴旗杆AB的高度约为13.5 m.
18.解:(1)根据三视图,可得这个几何体是三棱柱.
(2)表面积为×3×4×2+15×3+15×4+15×5=192.
19.解:如图,延长DH交BC的延长线于点M,延长AD交BC的延长线于点N.
可求得BM=3.4 m,DM=0.9 m.
由=,
可得MN=1.2(m).
所以BN=3.4+1.2=4.6(m).
由=,
可得AB=3.45(m).
所以大树的高度AB为3.45 m.
20.解:(1)-12 (2)B
(3)如图,
=×12×6=36,
=×12×30=180.
所以S△ABM的面积为36或180.
21.解:(1)根据图中尺寸计算铁皮的面积为(1×3)×2+(2×3)×2+(1×2)×2=22(m2).
(2)能做成一个长方体盒子,如图.其体积为3×1×2=6(m3).
22.解:如图,过点D作DE⊥AC于点E,作DF⊥AB于点F.设半圆圆心为O,连接OD.
∵点D在11点的刻度上,
∴∠COD=60°.
∴DE=OD·sin 60°=2×=(m),OE=OD·cos 60°=2×=1(m).
∴CE=2-1=1(m).
∵BA⊥AE,DE⊥AE,BA⊥DF,
∴∠FAE=∠AED=∠DFA=90°.
∴四边形AEDF为矩形.
∴DF=AE=11+1=12(m),AF=DE= m.
∵同时测得1 m长的标杆的影长为1.2 m,
∴=.∴BF=10(m).
∴AB=BF+FA=(10+)m.
答:旗杆AB的高度为(10+)m.
23.解:(1)能,理由:设圆锥侧面展开图(扇形)的圆心角为n°.
根据题意,得=7π,
解得n=180.
∴将圆形滤纸对折,将其中一层撑开,围成圆锥形,此时滤纸能紧贴此漏斗内壁.
(2)设滤纸围成的圆锥形底面圆的半径为r cm,高为h cm,
根据题意,
得2πr=,解得r=.
∴h==.
∴所求圆锥的体积为πr2h=π× = (cm3).
24.解:(1)11.3
(2)由题意,得DE=1.5 m,EC=2 m,BC=16 m.
根据镜面反射可知,∠ACB=∠ECD.
∵AB⊥BE,DE⊥BE,
∴∠ABC=∠DEC=90°.
∴△ACB∽△DCE.
∴=,
即=.
∴AB=12(m).
答:旗杆高度为12 m.
(3)设BG=x m,
由题意,得△DGC∽△DBA,△D'G'C'∽△D'BA.
∴=,=.
即=,=.
∴=.
整理得3.6=1.8,
解得x=22.5.经检验x=22.5是原方程的解且符合题意.
∴AB=1.8×÷1.5=28.8≈29(m).
答:雕塑高度约为29 m.
