期中评估测试卷(含答案) 2024-2025学年数学冀教版九年级下册
文档属性
| 名称 | 期中评估测试卷(含答案) 2024-2025学年数学冀教版九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 549.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-26 23:03:07 | ||
图片预览




文档简介
第二学期期中评估测试卷
(满分:120分 时间:120分钟)
一、选择题(本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.一条开口向上的抛物线的顶点坐标是(-1,2),则它对应的二次函数有( )
A.最大值1 B.最大值-1
C.最小值2 D.最小值-2
2.抛物线y=x2-2x+m2+2(m是常数)的顶点在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
3.如图,AB是☉O的切线,A为切点,连接OA,OB.若∠B=35°,则∠AOB的度数为 ( )
A.65° B.55° C.45° D.35°
4.如图,二次函数y=x2-4x+3的图像与x轴交于A,B两点,与y轴交于C点,则△ABC的面积为( )
A.6 B.3 C.4.5 D.5
5.如图,在平面直角坐标系中,已知P(6,8),M为OP中点,以P为圆心,6为半径作☉P,则下列结论:①点O在☉P外;②点M在☉P上;③x轴与☉P相离;④y轴与☉P相切.其中正确的有( )
A.1个 B.2个
C.3个 D.4个
6.若方程ax2+bx+c=0的两个根是-3和1,那么二次函数y=ax2+bx+c的图像向下平移3个单位长度,再向左平移2个单位长度,平移后新抛物线的对称轴是 ( )
A.直线x=-3 B.直线x=-2
C.直线x=-1 D.直线x=1
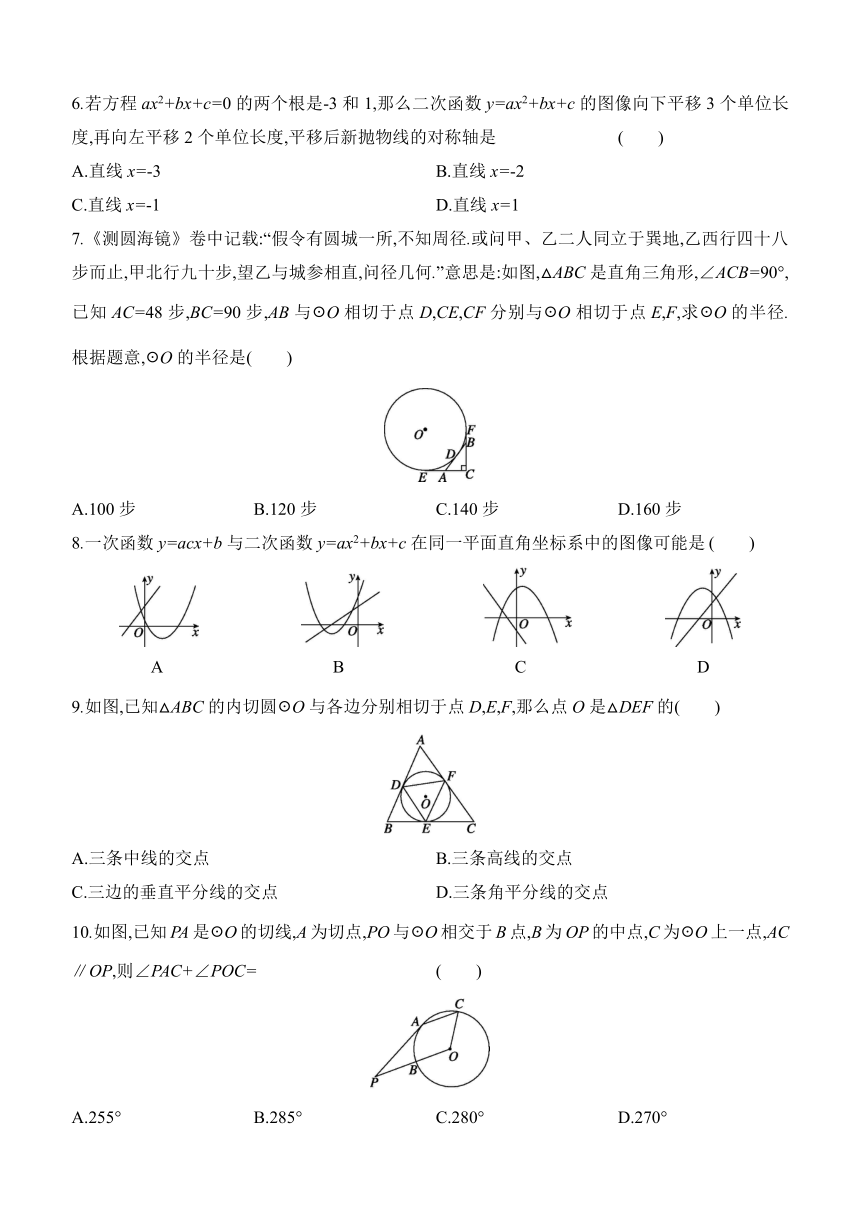
7.《测圆海镜》卷中记载:“假令有圆城一所,不知周径.或问甲、乙二人同立于巽地,乙西行四十八步而止,甲北行九十步,望乙与城参相直,问径几何.”意思是:如图,△ABC是直角三角形,∠ACB=90°,已知AC=48步,BC=90步,AB与☉O相切于点D,CE,CF分别与☉O相切于点E,F,求☉O的半径.根据题意,☉O的半径是( )
A.100步 B.120步 C.140步 D.160步
8.一次函数y=acx+b与二次函数y=ax2+bx+c在同一平面直角坐标系中的图像可能是 ( )
A B C D
9.如图,已知△ABC的内切圆☉O与各边分别相切于点D,E,F,那么点O是△DEF的( )
A.三条中线的交点 B.三条高线的交点
C.三边的垂直平分线的交点 D.三条角平分线的交点
10.如图,已知PA是☉O的切线,A为切点,PO与☉O相交于B点,B为OP的中点,C为☉O上一点,AC∥OP,则∠PAC+∠POC= ( )
A.255° B.285° C.280° D.270°
11.(2024乐山中考)已知二次函数y=x2-2x(-1≤x≤t-1),当x=-1时,函数取得最大值;当x=1时,函数取得最小值,则t的取值范围是 ( )
A.0C.2≤t≤4 D.t≥2
12.(2024齐齐哈尔中考)如图,在等腰直角三角形ABC中,∠BAC=90°,AB=12,动点E,F同时从点A出发,分别沿射线AB和射线AC的方向匀速运动,且速度大小相同,当点E停止运动时,点F也随之停止运动,连接EF,以EF为边向下作正方形EFGH,设点E运动的路程为x,正方形EFGH和等腰直角三角形ABC重合部分的面积为y.下列图像能反映y与x之间函数关系的是 ( )
A B C D
二、填空题(本大题共4个小题,每小题3分,共12分)
13.已知二次函数y=ax2+bx-2(a≠0)的图像的对称轴在y轴的左侧,请写出满足条件的一组a,b的值.这组值可以是 .
14.如图,已知坐标平面上有一顶点为A的抛物线,A点坐标为(-3,0),若此抛物线又与直线y=2交于B,C两点,且△ABC为正三角形,则可求得此抛物线与y轴的交点坐标为 .
15.如图,在☉O中,AB为直径,BD为弦,C为的中点,以点C为切点的切线与AB的延长线交于点E,连接AC,CD.
(1)若∠A=30°,AB=6,则的长是 (结果保留π).
(2)若=,则= .
16.如图,在△ABC中,AB=AC=10,D是边BC上一动点(不与点B,C重合),∠ADE=∠B=α,DE交线段AC于点E,且cos α=.
(1)若BD=8,则CE的长度是 .
(2)线段CE的取值范围是 .
三、解答题(本大题共8个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
17.(6分)如图,现打算用60 m的篱笆围成一个“日”字形菜园ABCD(含隔离栏EF),菜园的一面靠墙MN(39 m)(篱笆的宽度忽略不计).
(1)菜园面积可能为252 m2吗 若可能,求边AB的长;若不可能,请说明理由.
(2)因场地限制,菜园的宽度AB不能超过8 m,求该菜园面积的最大值.
18.(8分)如图,已知AB是☉O的直径,直线BC与☉O相切于点B,过点A作AD∥OC交☉O于点D,连接CD.
(1)求证:CD是☉O的切线.
(2)若AD=4,直径AB=12,求线段BC的长.
19.(8分)如图,二次函数y=ax2+bx的图像经过点A(2,4)与B(6,0).
(1)求a,b的值.
(2)C是该二次函数图像上A,B两点之间的一动点,横坐标为x(220.(8分)如图,CD是☉O的弦,AB是直径,连接AC,AD,OD,其中AC=CD,DA平分∠CDO,过点B作BE⊥CD交CD的延长线于点E.
(1)求证:BE是☉O的切线.
(2)若AB=12,求图中阴影部分的周长之和.
21.(9分)(2024烟台中考)每年5月的第三个星期日为全国助残日,今年的主题是“科技助残,共享美好生活”.康宁公司新研发了一批便携式轮椅计划在该月销售,根据市场调查,每辆轮椅盈利200元时,每天可售出60辆;单价每降低10元,每天可多售出4辆.公司决定在成本不变的情况下降价销售,但每辆轮椅的利润不低于180元,设每辆轮椅降价x元,每天的销售利润为y元.
(1)求y与x之间的函数关系式.每辆轮椅降价多少元时,每天的销售利润最大 最大利润为多少元
(2)全国助残日当天,公司共获得销售利润12 160元,请问:这天售出了多少辆轮椅
22.(10分)如图,在Rt△AOB中,∠AOB=90°,☉O与AB相交于点C,与AO相交于点E,连接CE,已知∠AOC=2∠ACE.
(1)求证:AB为☉O的切线.
(2)若AO=20,BO=15,求CE的长.
23.(11分)(2024青海中考)在如图所示的平面直角坐标系中,有一斜坡OA,从点O处抛出一个小球,落到点A处.小球在空中所经过的路线是抛物线y=-x2+bx的一部分.
(1)求抛物线的表达式.
(2)求抛物线最高点的坐标.
(3)斜坡上点B处有一棵树,B是OA的三等分点且OB24.(12分)(2024凉山州中考)如图,抛物线y=-x2+bx+c与直线y=x+2相交于A(-2,0),B(3,m)两点,与x轴相交于另一点C.
(1)求抛物线的表达式.
(2)P是直线AB上方抛物线上的一个动点(不与A,B重合),过点P作直线PD⊥x轴于点D,交直线AB于点E,当PE=2ED时,求点P的坐标.
(3)抛物线上是否存在点M使△ABM的面积等于△ABC面积的一半 若存在,请直接写出点M的坐标;若不存在,请说明理由.
【详解答案】
1.C 解析:∵一条开口向上的抛物线,顶点坐标为(-1,2),∴该二次函数有最小值2.故选C.
2.A 解析:∵y=x2-2x+m2+2=(x-1)2+(m2+1),∴顶点坐标为(1,m2+1).∵1>0,m2+1>0,∴顶点在第一象限.故选A.
3.B 解析:∵AB是☉O的切线,∴OA⊥AB.∴∠OAB=90°.∴∠AOB=90°-∠B=55°.故选B.
4.B 解析:由x2-4x+3=0,得x1=1,x2=3,∴A(1,0),B(3,0).∴AB=2.当x=0时,y=3.∴C(0,3).∴OC=3.
∴S△ABC=×AB×OC=3.故选B.
5.C 解析:过P点作PA⊥x轴于点A,作PB⊥y轴于点B(图略).∵P(6,8),∴PA=8>6,PB=6,得OP==10>6.∵M为OP中点,∴PM=5<6.∴点O在☉P外,点M在☉P内,①正确,②错误;x轴与☉P相离,y轴与☉P相切,③④正确.故选C.
6.A 解析:∵方程ax2+bx+c=0的两个根是-3和1,∴二次函数y=ax2+bx+c的图像与x轴的交点为(-3,0)和(1,0).∴二次函数y=ax2+bx+c的图像的对称轴为直线x==-1.把二次函数y=ax2+bx+c的图像向下平移3个单位长度,再向左平移2个单位长度,平移后新抛物线的对称轴是直线x=-1-2=-3.故选A.
7.B 解析:如图所示,连接OD,OE,OF.
∵CF,CE是☉O的切线,∴OF⊥CF,OE⊥CE.∴∠OFC=∠OEC=90°.∵∠ACB=90°,∴四边形OECF是矩形.
∵OE=OF,∴四边形OECF是正方形.设OE=OF=EC=FC=r步,则BF=FC-BC=(r-90)步,AE=EC-AC=(r-48)步,
∵AB,AE,BF是☉O的切线,∴BD=BF=(r-90)步,AD=AE=(r-48)步.
∵AB==102步,∴AB=AD+BD=102步.∴r-48+r-90=102.∴r=120.故选B.
8.B 解析:A.由抛物线,可知a>0,b<0,c>0,则ac>0;由直线,可知ac>0,b>0,故本选项错误.B.由抛物线,可知a>0,b>0,c>0,则ac>0;由直线,可知,ac>0,b>0,故本选项正确.C.由抛物线,可知a<0,b>0,c>0,则ac<0;由直线,可知ac<0,b<0,故本选项错误.D.由抛物线,可知a<0,b<0,c>0,则ac<0;由直线,可知ac>0,b>0,故本选项错误.故选B.
9.C 解析:∵☉O是△DEF的外接圆,∴点O是△DEF三边的垂直平分线的交点.故选C.
10.D 解析:如图,连接AB,OA.∵PA是☉O的切线,∴OA⊥PA.∴∠OAP=90°.∵B为OP的中点,∴AB=BP=BO.
∴△OAB为等边三角形.∴∠AOP=60°.∵AC∥OP,∴∠AOP=∠OAC=60°.∴△OAC为等边三角形.
∴∠AOC=60°.∴∠PAC+∠POC=90°+60°+60°+60°=270°.故选D.
11.C 解析:∵y=x2-2x=(x-1)2-1,∴图像开口向上,对称轴为直线x=1,顶点坐标为(1,-1).当x=-1时,y=3.∴(-1,3)关于对称轴对称的点的坐标为(3,3),∵当x=-1时,函数取得最大值;当x=1时,函数取得最小值,∴1≤t-1≤3,解得2≤t≤4.故选C.
12.A 解析:当HG与BC重合时(图略),设AE=x,由题意,可得EF=EH=x,BE=12-x.在Rt△EHB中,由勾股定理,可得BE2=BH2+EH2.+(x)2=(12-x)2.∴x=4(负值舍去).∴当00,∴图像为开口向上的抛物线的一部分.
如图,当HG在BC下方时,设AE=x.
∴EF=x,BE=12-x.∵∠AEF=∠B=45°,∠A=∠EOB=90°,∴△FAE∽△EOB.∴=.∴=.∴EO=.
∴当413.a=1,b=1(答案不唯一)
解析:∵二次函数y=ax2+bx-2(a≠0)的图像的对称轴在y轴的左侧,即-<0,∴a,b同号.∴满足条件的一组a,b的值是a=1,b=1(答案不唯一).
14. 解析:∵抛物线顶点A的坐标为(-3,0),∴可设二次函数的表达式为y=a(x+3)2.设B(-3-m,2),C(-3+m,2),
m>0.∴BC=2m.如图所示,过点A作AD⊥BC,
则BD=CD=m,AD=2.∵△ABC为正三角形,∴m=2tan 30°=.∵A点坐标为(-3,0),∴C.∵抛物线的表达式为y=a(x+3)2,将点C代入,得 a=2,解得a=.∴y=(x+3)2.当x=0时,y=.∴抛物线与y轴的交点为.
15.(1)2π (2) 解析:(1)如图1,连接OC,OD.∵C为的中点,∴=.
又∵∠A=30°,∴∠BOC=∠COD=2∠A=60°.∴∠BOD=120°.∵AB=6,∴OB=AB=3.∴=×π×3=2π.
图1
(2)如图2,连接OC.∵C为的中点,∴=.∴OC⊥BD.∵EC是☉O的切线,∴OC⊥EC.∴EC∥BD.∴=.∵=,∴=,设EB=2a,则AB=6a,BO=3a,EO=EB+BO=5a.∴EC==a=4a,AE=2a+6a=8a.
∴==.
图2
16.(1) (2)0∵∠ADE=∠B=α,∴cos B=cos α==.∴BG=×10=8.∴BC=2BG=16.
设BD=x,则CD=16-x,∵∠ADC=∠B+∠BAD,即α+∠CDE=∠B+∠BAD.∴∠CDE=∠BAD,而∠B=∠C.
∴△ABD∽△DCE.∴=,即=.∴CE=-x2+x,当x=8时,CE=.(2)CE=-x2+x=-(x-8)2+,故当x=8时,CE最大,最大值为,当x=0时,CE=0.∵D是边BC上一动点(不与点B,C重合),∴017.解:(1)可能.设AB=x m,则BC=(60-3x)m,依题意,得
x=252,
即x2-20x+84=0,
解得x1=6,x2=14.
当x1=6时,60-3x=42>39,舍去,
当x2=14时,60-3x=18<39,成立.
答:花园面积可能是252 m2,此时边AB的长为14 m.
(2)设AB=x m,则BC=(60-3x)m,依题意,得
S=x(60-3x)=-3x2+60x=-3(x-10)2+300.
∵-3<0,
∴当x<10时,y随x的增大而增大.
∵x≤8,
∴当x=8时,y最大,最大为288.
答:该菜园面积的最大值为288 m2.
18.(1)证明:连接OD,如图.
∵OA=OD,
∴∠ODA=∠OAD.
∵AD∥CO,
∴∠COD=∠ODA,∠COB=∠OAD.
∴∠COD=∠COB.
∵OD=OB,OC=OC,
∴△ODC≌△OBC(SAS).
∴∠ODC=∠OBC.
∵CB是☉O的切线且OB为半径,
∴∠OBC=90°.
∴∠ODC=90°.
∴OD⊥CD.
又∵CD经过半径OD的外端点D,
∴CD为☉O的切线.
(2)解:连接BD,如图.
∵AB是☉O的直径,∴∠ADB=90°.在Rt△ADB中,BD===8.
∵∠ADB=∠OBC=90°,且∠BAD=∠COB,
∴△ADB∽△OBC.
∴=,即=,
∴BC=12.
19.解:(1)抛物线为y=ax2+bx,将点A(2,4),B(6,0)代入,得解得
(2)如图,过点A作x轴的垂线,垂足为D,可知其坐标为(2,0),连接CD,过点C作CE⊥AD,CF⊥x轴,垂足分别为E,F.
∵S△OAD=OD·AD=×2×4=4,S△ACD=AD·CE=×4×(x-2)=2x-4,S△BCD=BD·CF=×4×=-x2+6x,
∴S=S△OAD+S△ACD+S△BCD=4+2x-4-x2+6x=-x2+8x.
∴S关于x的函数表达式为S=-x2+8x(220.(1)证明:∵AO=OD,
∴∠OAD=∠ODA.
∵DA平分∠CDO,
∴∠CDA=∠ODA.
∴∠OAD=∠CDA.
∴CD∥AB.
∵BE⊥CD,∴∠E=90°.
∴∠ABE=90°.
∴BE⊥AB.
∴BE是☉O的切线.
(2)解:如图,连接BD,OC.
∵AC=CD,
∴∠CAD=∠CDA.
∵∠CDA=∠OAD,
∴∠CAD=∠CDA=∠OAD.
∴∠COD=∠COA=∠BOD=180°×=60°.
∴△BOD,△AOC都是等边三角形.
∴AC=BD=AO=6,===2π.
∵∠OBE=90°,
∴∠DBE=30°.
∵∠E=90°,
∴DE=BD=3,BE=BD·cos∠DBE=3.
∴图中阴影部分的周长之和为2π+6+3+3+2π=9+3+4π.
21.解:(1)由题意,得
y=(200-x)=-x2+20x+12 000=-(x-25)2+12 250.
∵每辆轮椅的利润不低于180元,
∴200-x≥180.
∴x≤20.
∵当x<25时,y随x的增大而增大,
∴当x=20时,每天的利润最大,为-+12 250=12 240(元).
∴y与x之间的函数关系式为y=-+12 250;
每辆轮椅降价20元时,每天的利润最大,为12 240元.
(2)当y=12 160时,-x2+20x+12 000=12 160,
解得x1=10,x2=40(不合题意,舍去).
∴60+×4=64(辆).
答:这天售出了64辆轮椅.
22.(1)证明:∵OC=OE,
∴∠OCE=∠OEC.
∵∠AOC=2∠ACE,
∴∠OCA=∠OCE+∠ACE=(2∠OCE+∠AOC)=×180°=90°.
∴OC⊥AB.∴AB为☉O的切线.
(2)解:如图,过点E作EH⊥AC于点H.
∵AO=20,BO=15,
∴AB===25.
∵OA·OB=AB·OC,
即×20×15=×25×OC,
∴OC=12,
∴AE=OA-OE=20-12=8.
∵EH⊥AC,OC⊥AC,
∴∠AHE=∠ACO=90°.
∴EH∥OC.
∴△AEH∽△AOC.
∴=,即=.
∴EH=.
∵BC===9,
∴AC=AB-BC=25-9=16.
∵AH===,
∴CH=AC-AH=16-=.
∴CE===.
23.解:(1)∵点A是抛物线y=-x2+bx上的一点,
把点A代入y=-x2+bx中,得-32+3b=,
解得b=.
∴抛物线的表达式为y=-x2+x.
(2)由(1),得y=-x2+x=-.
∴抛物线最高点的坐标为.
(3)如图,过点A,B分别作x轴的垂线,垂足分别是E,D,
∵∠BOD=∠AOE,
∠BDO=∠AEO=90°,
∴△OBD∽△OAE.
∴==.
又∵B是OA的三等分点,
且OB∴=.
∵A,
∴AE=,OE=3.
∴==.
解得BD=.
∵==,
解得OD=1.
∴点C的横坐标为1.
将x=1代入y=-x2+x中,得y=-12+×1=.
∴点C的坐标为.
∴CD=.
∴CB=CD-BD==2.
答:这棵树的高度为2.
24.解:(1)把B(3,m)代入y=x+2,得m=3+2=5.
∴B(3,5).
把A(-2,0),B(3,5)代入y=-x2+bx+c,得
解得
∴抛物线的表达式为y=-x2+2x+8.
(2)设P(t,-t2+2t+8),则E(t,t+2),D(t,0).
∵PE=2ED,
∴-t2+2t+8-(t+2)=2(t+2).
解得t=1或t=-2(此时点P不在直线AB上方,舍去).
∴点P的坐标为(1,9).
(3)抛物线上存在点M,使△ABM的面积等于△ABC面积的一半.点M的坐标为或或或.
解法提示:过点M作MK∥y轴交直线AB于点K,过点B作BE⊥MK,延长MK交x轴于点F,如图.
在y=-x2+2x+8中,令y=0得0=-x2+2x+8,
解得x=-2或x=4.
∴A(-2,0),C(4,0).∴AC=6.
∵B(3,5),
∴S△ABC=×6×5=15.
设M(m,-m2+2 m+8),则K(m,m+2).
∴MK==
.
∴S△ABM=MK·
=×5
=.
∵△ABM的面积等于△ABC面积的一半,
∴=×15.
∴=3.
∴-m2+m+6=3或-m2+m+6=-3.
解得m=或m=.
∴M的坐标为或或或.
(满分:120分 时间:120分钟)
一、选择题(本大题共12个小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.一条开口向上的抛物线的顶点坐标是(-1,2),则它对应的二次函数有( )
A.最大值1 B.最大值-1
C.最小值2 D.最小值-2
2.抛物线y=x2-2x+m2+2(m是常数)的顶点在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
3.如图,AB是☉O的切线,A为切点,连接OA,OB.若∠B=35°,则∠AOB的度数为 ( )
A.65° B.55° C.45° D.35°
4.如图,二次函数y=x2-4x+3的图像与x轴交于A,B两点,与y轴交于C点,则△ABC的面积为( )
A.6 B.3 C.4.5 D.5
5.如图,在平面直角坐标系中,已知P(6,8),M为OP中点,以P为圆心,6为半径作☉P,则下列结论:①点O在☉P外;②点M在☉P上;③x轴与☉P相离;④y轴与☉P相切.其中正确的有( )
A.1个 B.2个
C.3个 D.4个
6.若方程ax2+bx+c=0的两个根是-3和1,那么二次函数y=ax2+bx+c的图像向下平移3个单位长度,再向左平移2个单位长度,平移后新抛物线的对称轴是 ( )
A.直线x=-3 B.直线x=-2
C.直线x=-1 D.直线x=1
7.《测圆海镜》卷中记载:“假令有圆城一所,不知周径.或问甲、乙二人同立于巽地,乙西行四十八步而止,甲北行九十步,望乙与城参相直,问径几何.”意思是:如图,△ABC是直角三角形,∠ACB=90°,已知AC=48步,BC=90步,AB与☉O相切于点D,CE,CF分别与☉O相切于点E,F,求☉O的半径.根据题意,☉O的半径是( )
A.100步 B.120步 C.140步 D.160步
8.一次函数y=acx+b与二次函数y=ax2+bx+c在同一平面直角坐标系中的图像可能是 ( )
A B C D
9.如图,已知△ABC的内切圆☉O与各边分别相切于点D,E,F,那么点O是△DEF的( )
A.三条中线的交点 B.三条高线的交点
C.三边的垂直平分线的交点 D.三条角平分线的交点
10.如图,已知PA是☉O的切线,A为切点,PO与☉O相交于B点,B为OP的中点,C为☉O上一点,AC∥OP,则∠PAC+∠POC= ( )
A.255° B.285° C.280° D.270°
11.(2024乐山中考)已知二次函数y=x2-2x(-1≤x≤t-1),当x=-1时,函数取得最大值;当x=1时,函数取得最小值,则t的取值范围是 ( )
A.0
12.(2024齐齐哈尔中考)如图,在等腰直角三角形ABC中,∠BAC=90°,AB=12,动点E,F同时从点A出发,分别沿射线AB和射线AC的方向匀速运动,且速度大小相同,当点E停止运动时,点F也随之停止运动,连接EF,以EF为边向下作正方形EFGH,设点E运动的路程为x,正方形EFGH和等腰直角三角形ABC重合部分的面积为y.下列图像能反映y与x之间函数关系的是 ( )
A B C D
二、填空题(本大题共4个小题,每小题3分,共12分)
13.已知二次函数y=ax2+bx-2(a≠0)的图像的对称轴在y轴的左侧,请写出满足条件的一组a,b的值.这组值可以是 .
14.如图,已知坐标平面上有一顶点为A的抛物线,A点坐标为(-3,0),若此抛物线又与直线y=2交于B,C两点,且△ABC为正三角形,则可求得此抛物线与y轴的交点坐标为 .
15.如图,在☉O中,AB为直径,BD为弦,C为的中点,以点C为切点的切线与AB的延长线交于点E,连接AC,CD.
(1)若∠A=30°,AB=6,则的长是 (结果保留π).
(2)若=,则= .
16.如图,在△ABC中,AB=AC=10,D是边BC上一动点(不与点B,C重合),∠ADE=∠B=α,DE交线段AC于点E,且cos α=.
(1)若BD=8,则CE的长度是 .
(2)线段CE的取值范围是 .
三、解答题(本大题共8个小题,共72分.解答应写出文字说明、证明过程或演算步骤)
17.(6分)如图,现打算用60 m的篱笆围成一个“日”字形菜园ABCD(含隔离栏EF),菜园的一面靠墙MN(39 m)(篱笆的宽度忽略不计).
(1)菜园面积可能为252 m2吗 若可能,求边AB的长;若不可能,请说明理由.
(2)因场地限制,菜园的宽度AB不能超过8 m,求该菜园面积的最大值.
18.(8分)如图,已知AB是☉O的直径,直线BC与☉O相切于点B,过点A作AD∥OC交☉O于点D,连接CD.
(1)求证:CD是☉O的切线.
(2)若AD=4,直径AB=12,求线段BC的长.
19.(8分)如图,二次函数y=ax2+bx的图像经过点A(2,4)与B(6,0).
(1)求a,b的值.
(2)C是该二次函数图像上A,B两点之间的一动点,横坐标为x(2
(1)求证:BE是☉O的切线.
(2)若AB=12,求图中阴影部分的周长之和.
21.(9分)(2024烟台中考)每年5月的第三个星期日为全国助残日,今年的主题是“科技助残,共享美好生活”.康宁公司新研发了一批便携式轮椅计划在该月销售,根据市场调查,每辆轮椅盈利200元时,每天可售出60辆;单价每降低10元,每天可多售出4辆.公司决定在成本不变的情况下降价销售,但每辆轮椅的利润不低于180元,设每辆轮椅降价x元,每天的销售利润为y元.
(1)求y与x之间的函数关系式.每辆轮椅降价多少元时,每天的销售利润最大 最大利润为多少元
(2)全国助残日当天,公司共获得销售利润12 160元,请问:这天售出了多少辆轮椅
22.(10分)如图,在Rt△AOB中,∠AOB=90°,☉O与AB相交于点C,与AO相交于点E,连接CE,已知∠AOC=2∠ACE.
(1)求证:AB为☉O的切线.
(2)若AO=20,BO=15,求CE的长.
23.(11分)(2024青海中考)在如图所示的平面直角坐标系中,有一斜坡OA,从点O处抛出一个小球,落到点A处.小球在空中所经过的路线是抛物线y=-x2+bx的一部分.
(1)求抛物线的表达式.
(2)求抛物线最高点的坐标.
(3)斜坡上点B处有一棵树,B是OA的三等分点且OB
(1)求抛物线的表达式.
(2)P是直线AB上方抛物线上的一个动点(不与A,B重合),过点P作直线PD⊥x轴于点D,交直线AB于点E,当PE=2ED时,求点P的坐标.
(3)抛物线上是否存在点M使△ABM的面积等于△ABC面积的一半 若存在,请直接写出点M的坐标;若不存在,请说明理由.
【详解答案】
1.C 解析:∵一条开口向上的抛物线,顶点坐标为(-1,2),∴该二次函数有最小值2.故选C.
2.A 解析:∵y=x2-2x+m2+2=(x-1)2+(m2+1),∴顶点坐标为(1,m2+1).∵1>0,m2+1>0,∴顶点在第一象限.故选A.
3.B 解析:∵AB是☉O的切线,∴OA⊥AB.∴∠OAB=90°.∴∠AOB=90°-∠B=55°.故选B.
4.B 解析:由x2-4x+3=0,得x1=1,x2=3,∴A(1,0),B(3,0).∴AB=2.当x=0时,y=3.∴C(0,3).∴OC=3.
∴S△ABC=×AB×OC=3.故选B.
5.C 解析:过P点作PA⊥x轴于点A,作PB⊥y轴于点B(图略).∵P(6,8),∴PA=8>6,PB=6,得OP==10>6.∵M为OP中点,∴PM=5<6.∴点O在☉P外,点M在☉P内,①正确,②错误;x轴与☉P相离,y轴与☉P相切,③④正确.故选C.
6.A 解析:∵方程ax2+bx+c=0的两个根是-3和1,∴二次函数y=ax2+bx+c的图像与x轴的交点为(-3,0)和(1,0).∴二次函数y=ax2+bx+c的图像的对称轴为直线x==-1.把二次函数y=ax2+bx+c的图像向下平移3个单位长度,再向左平移2个单位长度,平移后新抛物线的对称轴是直线x=-1-2=-3.故选A.
7.B 解析:如图所示,连接OD,OE,OF.
∵CF,CE是☉O的切线,∴OF⊥CF,OE⊥CE.∴∠OFC=∠OEC=90°.∵∠ACB=90°,∴四边形OECF是矩形.
∵OE=OF,∴四边形OECF是正方形.设OE=OF=EC=FC=r步,则BF=FC-BC=(r-90)步,AE=EC-AC=(r-48)步,
∵AB,AE,BF是☉O的切线,∴BD=BF=(r-90)步,AD=AE=(r-48)步.
∵AB==102步,∴AB=AD+BD=102步.∴r-48+r-90=102.∴r=120.故选B.
8.B 解析:A.由抛物线,可知a>0,b<0,c>0,则ac>0;由直线,可知ac>0,b>0,故本选项错误.B.由抛物线,可知a>0,b>0,c>0,则ac>0;由直线,可知,ac>0,b>0,故本选项正确.C.由抛物线,可知a<0,b>0,c>0,则ac<0;由直线,可知ac<0,b<0,故本选项错误.D.由抛物线,可知a<0,b<0,c>0,则ac<0;由直线,可知ac>0,b>0,故本选项错误.故选B.
9.C 解析:∵☉O是△DEF的外接圆,∴点O是△DEF三边的垂直平分线的交点.故选C.
10.D 解析:如图,连接AB,OA.∵PA是☉O的切线,∴OA⊥PA.∴∠OAP=90°.∵B为OP的中点,∴AB=BP=BO.
∴△OAB为等边三角形.∴∠AOP=60°.∵AC∥OP,∴∠AOP=∠OAC=60°.∴△OAC为等边三角形.
∴∠AOC=60°.∴∠PAC+∠POC=90°+60°+60°+60°=270°.故选D.
11.C 解析:∵y=x2-2x=(x-1)2-1,∴图像开口向上,对称轴为直线x=1,顶点坐标为(1,-1).当x=-1时,y=3.∴(-1,3)关于对称轴对称的点的坐标为(3,3),∵当x=-1时,函数取得最大值;当x=1时,函数取得最小值,∴1≤t-1≤3,解得2≤t≤4.故选C.
12.A 解析:当HG与BC重合时(图略),设AE=x,由题意,可得EF=EH=x,BE=12-x.在Rt△EHB中,由勾股定理,可得BE2=BH2+EH2.+(x)2=(12-x)2.∴x=4(负值舍去).∴当0
如图,当HG在BC下方时,设AE=x.
∴EF=x,BE=12-x.∵∠AEF=∠B=45°,∠A=∠EOB=90°,∴△FAE∽△EOB.∴=.∴=.∴EO=.
∴当4
解析:∵二次函数y=ax2+bx-2(a≠0)的图像的对称轴在y轴的左侧,即-<0,∴a,b同号.∴满足条件的一组a,b的值是a=1,b=1(答案不唯一).
14. 解析:∵抛物线顶点A的坐标为(-3,0),∴可设二次函数的表达式为y=a(x+3)2.设B(-3-m,2),C(-3+m,2),
m>0.∴BC=2m.如图所示,过点A作AD⊥BC,
则BD=CD=m,AD=2.∵△ABC为正三角形,∴m=2tan 30°=.∵A点坐标为(-3,0),∴C.∵抛物线的表达式为y=a(x+3)2,将点C代入,得 a=2,解得a=.∴y=(x+3)2.当x=0时,y=.∴抛物线与y轴的交点为.
15.(1)2π (2) 解析:(1)如图1,连接OC,OD.∵C为的中点,∴=.
又∵∠A=30°,∴∠BOC=∠COD=2∠A=60°.∴∠BOD=120°.∵AB=6,∴OB=AB=3.∴=×π×3=2π.
图1
(2)如图2,连接OC.∵C为的中点,∴=.∴OC⊥BD.∵EC是☉O的切线,∴OC⊥EC.∴EC∥BD.∴=.∵=,∴=,设EB=2a,则AB=6a,BO=3a,EO=EB+BO=5a.∴EC==a=4a,AE=2a+6a=8a.
∴==.
图2
16.(1) (2)0
设BD=x,则CD=16-x,∵∠ADC=∠B+∠BAD,即α+∠CDE=∠B+∠BAD.∴∠CDE=∠BAD,而∠B=∠C.
∴△ABD∽△DCE.∴=,即=.∴CE=-x2+x,当x=8时,CE=.(2)CE=-x2+x=-(x-8)2+,故当x=8时,CE最大,最大值为,当x=0时,CE=0.∵D是边BC上一动点(不与点B,C重合),∴0
x=252,
即x2-20x+84=0,
解得x1=6,x2=14.
当x1=6时,60-3x=42>39,舍去,
当x2=14时,60-3x=18<39,成立.
答:花园面积可能是252 m2,此时边AB的长为14 m.
(2)设AB=x m,则BC=(60-3x)m,依题意,得
S=x(60-3x)=-3x2+60x=-3(x-10)2+300.
∵-3<0,
∴当x<10时,y随x的增大而增大.
∵x≤8,
∴当x=8时,y最大,最大为288.
答:该菜园面积的最大值为288 m2.
18.(1)证明:连接OD,如图.
∵OA=OD,
∴∠ODA=∠OAD.
∵AD∥CO,
∴∠COD=∠ODA,∠COB=∠OAD.
∴∠COD=∠COB.
∵OD=OB,OC=OC,
∴△ODC≌△OBC(SAS).
∴∠ODC=∠OBC.
∵CB是☉O的切线且OB为半径,
∴∠OBC=90°.
∴∠ODC=90°.
∴OD⊥CD.
又∵CD经过半径OD的外端点D,
∴CD为☉O的切线.
(2)解:连接BD,如图.
∵AB是☉O的直径,∴∠ADB=90°.在Rt△ADB中,BD===8.
∵∠ADB=∠OBC=90°,且∠BAD=∠COB,
∴△ADB∽△OBC.
∴=,即=,
∴BC=12.
19.解:(1)抛物线为y=ax2+bx,将点A(2,4),B(6,0)代入,得解得
(2)如图,过点A作x轴的垂线,垂足为D,可知其坐标为(2,0),连接CD,过点C作CE⊥AD,CF⊥x轴,垂足分别为E,F.
∵S△OAD=OD·AD=×2×4=4,S△ACD=AD·CE=×4×(x-2)=2x-4,S△BCD=BD·CF=×4×=-x2+6x,
∴S=S△OAD+S△ACD+S△BCD=4+2x-4-x2+6x=-x2+8x.
∴S关于x的函数表达式为S=-x2+8x(2
∴∠OAD=∠ODA.
∵DA平分∠CDO,
∴∠CDA=∠ODA.
∴∠OAD=∠CDA.
∴CD∥AB.
∵BE⊥CD,∴∠E=90°.
∴∠ABE=90°.
∴BE⊥AB.
∴BE是☉O的切线.
(2)解:如图,连接BD,OC.
∵AC=CD,
∴∠CAD=∠CDA.
∵∠CDA=∠OAD,
∴∠CAD=∠CDA=∠OAD.
∴∠COD=∠COA=∠BOD=180°×=60°.
∴△BOD,△AOC都是等边三角形.
∴AC=BD=AO=6,===2π.
∵∠OBE=90°,
∴∠DBE=30°.
∵∠E=90°,
∴DE=BD=3,BE=BD·cos∠DBE=3.
∴图中阴影部分的周长之和为2π+6+3+3+2π=9+3+4π.
21.解:(1)由题意,得
y=(200-x)=-x2+20x+12 000=-(x-25)2+12 250.
∵每辆轮椅的利润不低于180元,
∴200-x≥180.
∴x≤20.
∵当x<25时,y随x的增大而增大,
∴当x=20时,每天的利润最大,为-+12 250=12 240(元).
∴y与x之间的函数关系式为y=-+12 250;
每辆轮椅降价20元时,每天的利润最大,为12 240元.
(2)当y=12 160时,-x2+20x+12 000=12 160,
解得x1=10,x2=40(不合题意,舍去).
∴60+×4=64(辆).
答:这天售出了64辆轮椅.
22.(1)证明:∵OC=OE,
∴∠OCE=∠OEC.
∵∠AOC=2∠ACE,
∴∠OCA=∠OCE+∠ACE=(2∠OCE+∠AOC)=×180°=90°.
∴OC⊥AB.∴AB为☉O的切线.
(2)解:如图,过点E作EH⊥AC于点H.
∵AO=20,BO=15,
∴AB===25.
∵OA·OB=AB·OC,
即×20×15=×25×OC,
∴OC=12,
∴AE=OA-OE=20-12=8.
∵EH⊥AC,OC⊥AC,
∴∠AHE=∠ACO=90°.
∴EH∥OC.
∴△AEH∽△AOC.
∴=,即=.
∴EH=.
∵BC===9,
∴AC=AB-BC=25-9=16.
∵AH===,
∴CH=AC-AH=16-=.
∴CE===.
23.解:(1)∵点A是抛物线y=-x2+bx上的一点,
把点A代入y=-x2+bx中,得-32+3b=,
解得b=.
∴抛物线的表达式为y=-x2+x.
(2)由(1),得y=-x2+x=-.
∴抛物线最高点的坐标为.
(3)如图,过点A,B分别作x轴的垂线,垂足分别是E,D,
∵∠BOD=∠AOE,
∠BDO=∠AEO=90°,
∴△OBD∽△OAE.
∴==.
又∵B是OA的三等分点,
且OB
∵A,
∴AE=,OE=3.
∴==.
解得BD=.
∵==,
解得OD=1.
∴点C的横坐标为1.
将x=1代入y=-x2+x中,得y=-12+×1=.
∴点C的坐标为.
∴CD=.
∴CB=CD-BD==2.
答:这棵树的高度为2.
24.解:(1)把B(3,m)代入y=x+2,得m=3+2=5.
∴B(3,5).
把A(-2,0),B(3,5)代入y=-x2+bx+c,得
解得
∴抛物线的表达式为y=-x2+2x+8.
(2)设P(t,-t2+2t+8),则E(t,t+2),D(t,0).
∵PE=2ED,
∴-t2+2t+8-(t+2)=2(t+2).
解得t=1或t=-2(此时点P不在直线AB上方,舍去).
∴点P的坐标为(1,9).
(3)抛物线上存在点M,使△ABM的面积等于△ABC面积的一半.点M的坐标为或或或.
解法提示:过点M作MK∥y轴交直线AB于点K,过点B作BE⊥MK,延长MK交x轴于点F,如图.
在y=-x2+2x+8中,令y=0得0=-x2+2x+8,
解得x=-2或x=4.
∴A(-2,0),C(4,0).∴AC=6.
∵B(3,5),
∴S△ABC=×6×5=15.
设M(m,-m2+2 m+8),则K(m,m+2).
∴MK==
.
∴S△ABM=MK·
=×5
=.
∵△ABM的面积等于△ABC面积的一半,
∴=×15.
∴=3.
∴-m2+m+6=3或-m2+m+6=-3.
解得m=或m=.
∴M的坐标为或或或.
同课章节目录
