26.1反比例函数本节综合题(含答案)
文档属性
| 名称 | 26.1反比例函数本节综合题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 445.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-27 13:55:58 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
26.1反比例函数本节综合题
一、单选题
1.若一次函数的图象经过点,则反比例函数的图象经过( )
A.第一、二象限 B.第二、四象限
C.第一、三象限 D.第三、四象限
2.已知点,都在反比例函数的图象上,且,则,的大小关系是( )
A. B. C. D.
3.下列各点中,在反比例函数的图像上的是( )
A. B. C. D.
4.反比例函数图象经过点和点,则的值为( )
A.10 B. C.3 D.
5.若点都在反比例函数的图象上,则的大小关系是( )
A. B. C. D.
6.已知y是x的反比例函数,下表给出了x与y的一些值,表中“▲”处的数为( )
A.3 B.-9 C.1 D.-1
7.已知反比例函数 ,下列结论中不正确的是
A.其图象经过点
B.其图象分别位于第一、第三象限
C.当 时,y随x的增大而减小
D.当 时,
8.已知点A (x1,y1),B (x2,y2)在反比例函数y=(k为常数)的图象上,且x1<0A.y1+y2<0 B.y1+y2>0 C.y1y2
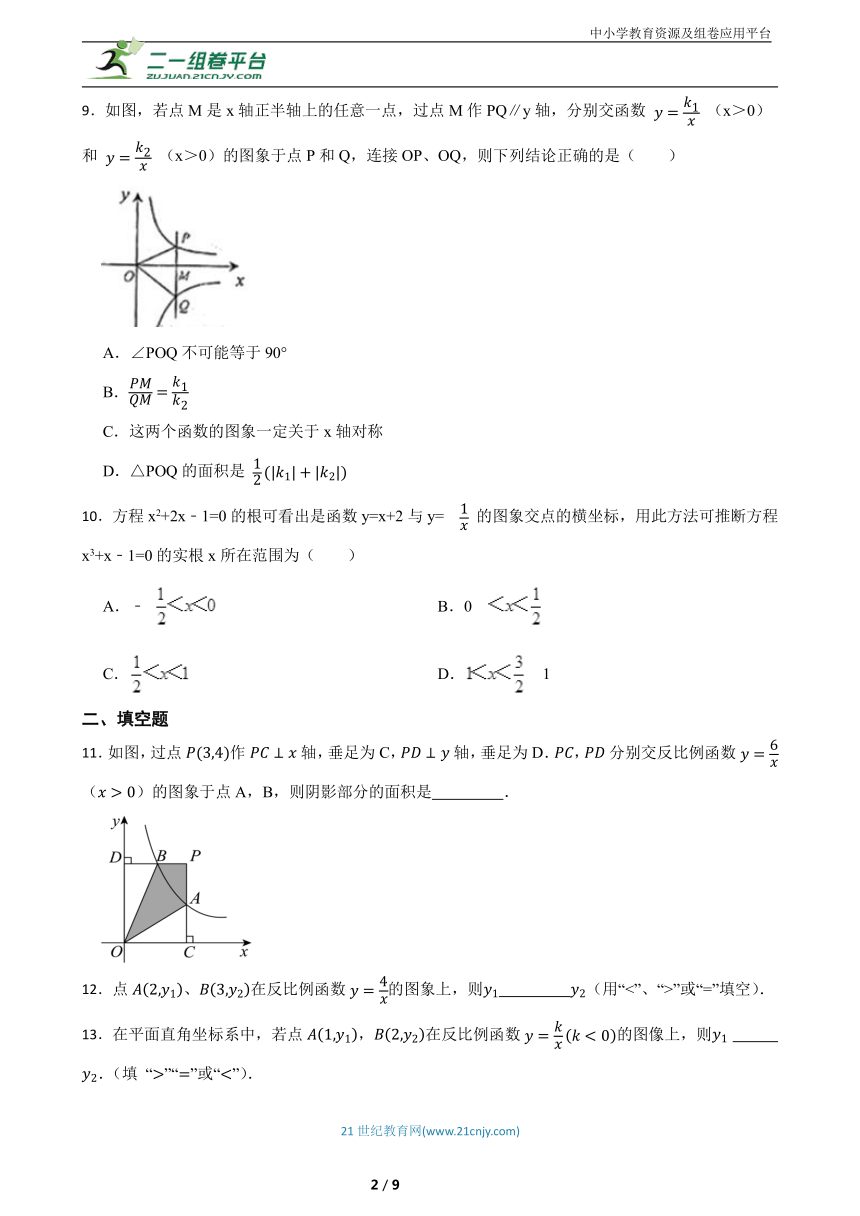
9.如图,若点M是x轴正半轴上的任意一点,过点M作PQ∥y轴,分别交函数 (x>0)和 (x>0)的图象于点P和Q,连接OP、OQ,则下列结论正确的是( )
A.∠POQ不可能等于90°
B.
C.这两个函数的图象一定关于x轴对称
D.△POQ的面积是
10.方程x2+2x﹣1=0的根可看出是函数y=x+2与y= 的图象交点的横坐标,用此方法可推断方程x3+x﹣1=0的实根x所在范围为( )
A.﹣ B.0
C. D. 1
二、填空题
11.如图,过点作轴,垂足为C,轴,垂足为D.,分别交反比例函数 ()的图象于点A,B,则阴影部分的面积是 .
12.点、在反比例函数的图象上,则 (用“<”、“>”或“=”填空).
13.在平面直角坐标系中,若点,在反比例函数的图像上,则 .(填 “”“”或“”).
14.设函数y= 与y=x﹣1的图象的交点坐标为(a,b),则 ﹣ 的值为 .
15.已知P1(x1,y1),P2(x2,y2)两点都在反比例函数 的图象上,且x1<x2<0,则yl y2(填“>”或“<”).
16.如图,正比例函数 y=x与反比例函数()的图象交于点A,,过点A作,交x轴于点B;作,交反比例函数的图象于点;过点作,交x轴于点;再作,交反比例函数的图象于点,依次进行下去…
根据以上信息,解答下列问题.
(1)k的值为 .
(2)点的横坐标为 .
三、计算题
17.如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象相交于第一,三象限内的,两点,与轴交于点.
(1)求该反比例函数和一次函数的表达式;
(2)在第三象限的反比例函数图象的一点,使得的面积等于18,求点的坐标.
18.如图,直线与函数的图象相交于点,与轴交于点,且,点是线段上一点.
(1)求的值;
(2)若与的面积比为,求点的坐标;
(3)将绕点逆时针旋转得到,点恰好落在函数的图像上,求点的坐标.
19.如图,抛物线L: (常数t>0)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线 于点P,且OA·MP=12.
(1)求k值;
(2)当t=1时,求AB长,并求直线MP与L对称轴之间的距离;
(3)把L在直线MP左侧部分的图象(含与直线MP的交点)记为G,用t表示图象G最高点的坐标;
(4)设L与双曲线有个交点的横坐标为x0,且满足4≤x0≤6,通过L位置随t变化的过程,直接写出t的取值范围.
四、解答题
20.如图,一次函数与反比例函数的图像相较于,两点.
(1)求一次函数与反比例函数的解析式;
(2)过点作轴,垂足为,求.
21.如图,直线与双曲线相交于、两点,与x轴交于点C.
(1)求直线的解析式;
(2)连接AO、OB,求的面积;
(3)请直接写出关于x的不等式的解集.
22.如图,一次函数的图象与反比例函数的图象交于,两点,与y轴交于点C.
(1)求反比例函数的表达式;
(2)当时,根据图象直接写出x的取值范围;
(3)设点E为第一象限内反比例函数图象上的点,当时,求直线BE的函数表达式.
23.已知,矩形在平面直角坐标系中的位置如图所示,点在轴的正半轴上,点在轴的正半轴上,已知点的坐标为,反比例函数的图象经过的中点,且与交于点,设直线的解析式为,连接,.
(1)求反比例函数的表达式和点E的坐标;
(2)点为轴正半轴上一点,若的面积等于的面积,求点的坐标;
(3)点P为x轴上一点,点Q为反比例函数图象上一点,是否存在点P、Q使得以点P,Q,D,E为顶点的四边形为平行四边形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
答案解析部分
1.【答案】B
【知识点】反比例函数与一次函数的交点问题
2.【答案】D
【知识点】反比例函数的性质
3.【答案】A
【知识点】反比例函数的概念
4.【答案】B
【知识点】待定系数法求反比例函数解析式
5.【答案】B
【知识点】反比例函数的性质
6.【答案】D
【知识点】待定系数法求反比例函数解析式;反比例函数图象上点的坐标特征
7.【答案】D
【知识点】反比例函数的性质
8.【答案】D
【知识点】反比例函数的图象;反比例函数的性质
9.【答案】D
【知识点】反比例函数图象的对称性;反比例函数的性质;反比例函数图象上点的坐标特征
10.【答案】C
【知识点】反比例函数的性质;二次函数与一元二次方程的综合应用
11.【答案】6
【知识点】反比例函数系数k的几何意义
12.【答案】
【知识点】反比例函数的性质
13.【答案】
【知识点】反比例函数的性质
14.【答案】﹣
【知识点】反比例函数与一次函数的交点问题
15.【答案】<
【知识点】反比例函数图象上点的坐标特征
16.【答案】1;
【知识点】反比例函数与一次函数的交点问题
17.【答案】(1),
(2)点坐标为
【知识点】待定系数法求一次函数解析式;待定系数法求反比例函数解析式
18.【答案】(1)
(2)
(3)或
【知识点】待定系数法求反比例函数解析式;反比例函数与一次函数的交点问题;坐标与图形变化﹣旋转
19.【答案】(1)解:设点P (x, y),则MP=y,由OA的中点为M知O4= 2x,代入OA.MP=12,
得2x.y=12,即xy=6.
∴k= xy=6.
(2)解:当t=1时,令y=0,
∴由B在A左边,得B (-3,0),A (1, 0),∴AB=4.
∵L的对称轴为x=-1,而M为( ,0),
∴MP与L对称轴的距离为 .
(3)解:∵A (t, 0),B (t-4,0),
∴L的对称轴为x=t-2.
又MP为x=
当t-2≤ ,即t≤4时,顶点(t-2,2)就是G的最高点;
当t>4时,L与MP的交点( , )就是G的最高点.
(4)解:5≤t≤8- 或7≤1≤8+
【知识点】反比例函数图象上点的坐标特征;二次函数图象上点的坐标特征;二次函数y=ax²+bx+c的图象;二次函数y=ax²+bx+c的性质
20.【答案】(1);
(2)5
【知识点】待定系数法求一次函数解析式;待定系数法求反比例函数解析式;反比例函数与一次函数的交点问题
21.【答案】(1);
(2);
(3).
【知识点】待定系数法求一次函数解析式;一次函数与不等式(组)的关系;反比例函数与一次函数的交点问题
22.【答案】(1)
(2)或
(3)
【知识点】反比例函数与一次函数的交点问题
23.【答案】(1),;
(2);
(3)或.
【知识点】待定系数法求反比例函数解析式;平行四边形的性质
21世纪教育网(www.21cnjy.com)
2 / 9
26.1反比例函数本节综合题
一、单选题
1.若一次函数的图象经过点,则反比例函数的图象经过( )
A.第一、二象限 B.第二、四象限
C.第一、三象限 D.第三、四象限
2.已知点,都在反比例函数的图象上,且,则,的大小关系是( )
A. B. C. D.
3.下列各点中,在反比例函数的图像上的是( )
A. B. C. D.
4.反比例函数图象经过点和点,则的值为( )
A.10 B. C.3 D.
5.若点都在反比例函数的图象上,则的大小关系是( )
A. B. C. D.
6.已知y是x的反比例函数,下表给出了x与y的一些值,表中“▲”处的数为( )
A.3 B.-9 C.1 D.-1
7.已知反比例函数 ,下列结论中不正确的是
A.其图象经过点
B.其图象分别位于第一、第三象限
C.当 时,y随x的增大而减小
D.当 时,
8.已知点A (x1,y1),B (x2,y2)在反比例函数y=(k为常数)的图象上,且x1<0
9.如图,若点M是x轴正半轴上的任意一点,过点M作PQ∥y轴,分别交函数 (x>0)和 (x>0)的图象于点P和Q,连接OP、OQ,则下列结论正确的是( )
A.∠POQ不可能等于90°
B.
C.这两个函数的图象一定关于x轴对称
D.△POQ的面积是
10.方程x2+2x﹣1=0的根可看出是函数y=x+2与y= 的图象交点的横坐标,用此方法可推断方程x3+x﹣1=0的实根x所在范围为( )
A.﹣ B.0
C. D. 1
二、填空题
11.如图,过点作轴,垂足为C,轴,垂足为D.,分别交反比例函数 ()的图象于点A,B,则阴影部分的面积是 .
12.点、在反比例函数的图象上,则 (用“<”、“>”或“=”填空).
13.在平面直角坐标系中,若点,在反比例函数的图像上,则 .(填 “”“”或“”).
14.设函数y= 与y=x﹣1的图象的交点坐标为(a,b),则 ﹣ 的值为 .
15.已知P1(x1,y1),P2(x2,y2)两点都在反比例函数 的图象上,且x1<x2<0,则yl y2(填“>”或“<”).
16.如图,正比例函数 y=x与反比例函数()的图象交于点A,,过点A作,交x轴于点B;作,交反比例函数的图象于点;过点作,交x轴于点;再作,交反比例函数的图象于点,依次进行下去…
根据以上信息,解答下列问题.
(1)k的值为 .
(2)点的横坐标为 .
三、计算题
17.如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象相交于第一,三象限内的,两点,与轴交于点.
(1)求该反比例函数和一次函数的表达式;
(2)在第三象限的反比例函数图象的一点,使得的面积等于18,求点的坐标.
18.如图,直线与函数的图象相交于点,与轴交于点,且,点是线段上一点.
(1)求的值;
(2)若与的面积比为,求点的坐标;
(3)将绕点逆时针旋转得到,点恰好落在函数的图像上,求点的坐标.
19.如图,抛物线L: (常数t>0)与x轴从左到右的交点为B,A,过线段OA的中点M作MP⊥x轴,交双曲线 于点P,且OA·MP=12.
(1)求k值;
(2)当t=1时,求AB长,并求直线MP与L对称轴之间的距离;
(3)把L在直线MP左侧部分的图象(含与直线MP的交点)记为G,用t表示图象G最高点的坐标;
(4)设L与双曲线有个交点的横坐标为x0,且满足4≤x0≤6,通过L位置随t变化的过程,直接写出t的取值范围.
四、解答题
20.如图,一次函数与反比例函数的图像相较于,两点.
(1)求一次函数与反比例函数的解析式;
(2)过点作轴,垂足为,求.
21.如图,直线与双曲线相交于、两点,与x轴交于点C.
(1)求直线的解析式;
(2)连接AO、OB,求的面积;
(3)请直接写出关于x的不等式的解集.
22.如图,一次函数的图象与反比例函数的图象交于,两点,与y轴交于点C.
(1)求反比例函数的表达式;
(2)当时,根据图象直接写出x的取值范围;
(3)设点E为第一象限内反比例函数图象上的点,当时,求直线BE的函数表达式.
23.已知,矩形在平面直角坐标系中的位置如图所示,点在轴的正半轴上,点在轴的正半轴上,已知点的坐标为,反比例函数的图象经过的中点,且与交于点,设直线的解析式为,连接,.
(1)求反比例函数的表达式和点E的坐标;
(2)点为轴正半轴上一点,若的面积等于的面积,求点的坐标;
(3)点P为x轴上一点,点Q为反比例函数图象上一点,是否存在点P、Q使得以点P,Q,D,E为顶点的四边形为平行四边形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
答案解析部分
1.【答案】B
【知识点】反比例函数与一次函数的交点问题
2.【答案】D
【知识点】反比例函数的性质
3.【答案】A
【知识点】反比例函数的概念
4.【答案】B
【知识点】待定系数法求反比例函数解析式
5.【答案】B
【知识点】反比例函数的性质
6.【答案】D
【知识点】待定系数法求反比例函数解析式;反比例函数图象上点的坐标特征
7.【答案】D
【知识点】反比例函数的性质
8.【答案】D
【知识点】反比例函数的图象;反比例函数的性质
9.【答案】D
【知识点】反比例函数图象的对称性;反比例函数的性质;反比例函数图象上点的坐标特征
10.【答案】C
【知识点】反比例函数的性质;二次函数与一元二次方程的综合应用
11.【答案】6
【知识点】反比例函数系数k的几何意义
12.【答案】
【知识点】反比例函数的性质
13.【答案】
【知识点】反比例函数的性质
14.【答案】﹣
【知识点】反比例函数与一次函数的交点问题
15.【答案】<
【知识点】反比例函数图象上点的坐标特征
16.【答案】1;
【知识点】反比例函数与一次函数的交点问题
17.【答案】(1),
(2)点坐标为
【知识点】待定系数法求一次函数解析式;待定系数法求反比例函数解析式
18.【答案】(1)
(2)
(3)或
【知识点】待定系数法求反比例函数解析式;反比例函数与一次函数的交点问题;坐标与图形变化﹣旋转
19.【答案】(1)解:设点P (x, y),则MP=y,由OA的中点为M知O4= 2x,代入OA.MP=12,
得2x.y=12,即xy=6.
∴k= xy=6.
(2)解:当t=1时,令y=0,
∴由B在A左边,得B (-3,0),A (1, 0),∴AB=4.
∵L的对称轴为x=-1,而M为( ,0),
∴MP与L对称轴的距离为 .
(3)解:∵A (t, 0),B (t-4,0),
∴L的对称轴为x=t-2.
又MP为x=
当t-2≤ ,即t≤4时,顶点(t-2,2)就是G的最高点;
当t>4时,L与MP的交点( , )就是G的最高点.
(4)解:5≤t≤8- 或7≤1≤8+
【知识点】反比例函数图象上点的坐标特征;二次函数图象上点的坐标特征;二次函数y=ax²+bx+c的图象;二次函数y=ax²+bx+c的性质
20.【答案】(1);
(2)5
【知识点】待定系数法求一次函数解析式;待定系数法求反比例函数解析式;反比例函数与一次函数的交点问题
21.【答案】(1);
(2);
(3).
【知识点】待定系数法求一次函数解析式;一次函数与不等式(组)的关系;反比例函数与一次函数的交点问题
22.【答案】(1)
(2)或
(3)
【知识点】反比例函数与一次函数的交点问题
23.【答案】(1),;
(2);
(3)或.
【知识点】待定系数法求反比例函数解析式;平行四边形的性质
21世纪教育网(www.21cnjy.com)
2 / 9
