26.2实际问题与反比例函数(含答案)
文档属性
| 名称 | 26.2实际问题与反比例函数(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 555.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-27 13:56:53 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
26.2实际问题与反比例函数
一、单选题
1.已知甲、乙两地相距40米,汽车从甲地匀速行驶到乙地,则汽车行驶时间t(单位:小时)关于行驶速度v(单位:千米/小时)的函数关系式是( )
A.t=40v B. C. D.
2.A,B两城间的距离为15千米,一人行路的平均速度每小时不少于3千米,也不多于5千米,则表示此人由A到B的行路速度x(千米/小时)与所用时间y(小时)的关系y= 的函数图象是( )
A. B.
C. D.
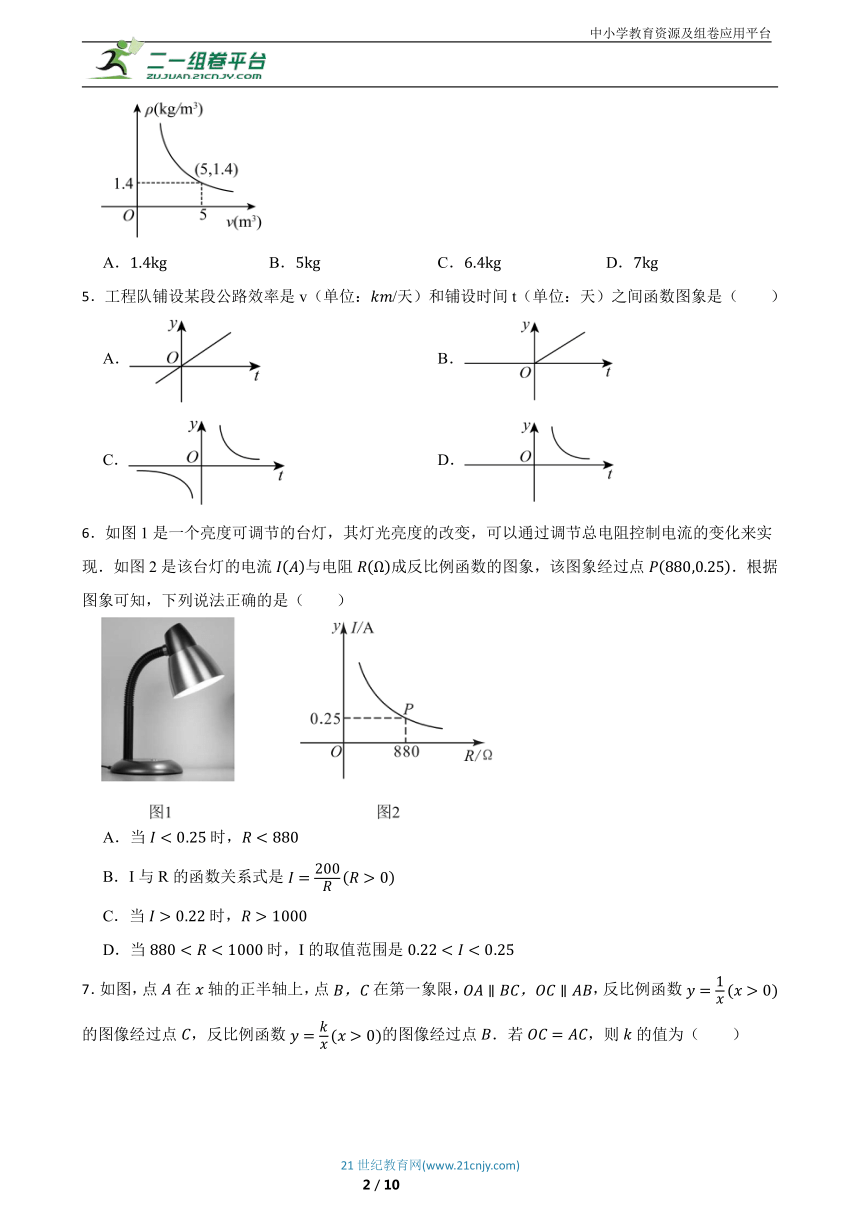
3.在一个密闭的容器内装有一定质量的某种气体,当它的容积V改变时,气体的密度也随之改变,与V之间在一定范围内满足,如图所示.当为时,V的值是( )
A. B. C. D.
4.在一个可以改变容积的密闭容器内,装有质量为m 的气体,当改变容积V时,气体的密度ρ也随之改变,与V在一定范围内满足,它的图象如的质量m为( )
A. B. C. D.
5.工程队铺设某段公路效率是v(单位:/天)和铺设时间t(单位:天)之间函数图象是( )
A. B.
C. D.
6.如图1是一个亮度可调节的台灯,其灯光亮度的改变,可以通过调节总电阻控制电流的变化来实现.如图2是该台灯的电流与电阻成反比例函数的图象,该图象经过点.根据图象可知,下列说法正确的是( )
A.当时,
B.I与R的函数关系式是
C.当时,
D.当时,I的取值范围是
7.如图,点在轴的正半轴上,点在第一象限,,反比例函数的图像经过点,反比例函数的图像经过点.若,则的值为( )
A.2 B.3 C.4 D.5
8.已知一个矩形的面积为20,若设长为a,宽为b,则能大致反映a与b之间函数关系的图象为( )
A. B.
C. D.
9.在做拉面的过程中渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(mm)与面条的粗细s(mm )(横截面积)的对应数据如下表.根据表中数据,可得y关于s的函数表达式为( )
面条的总长度y(mm) 100 200 400 800 2000
面条的粗细s(mm2) 12.80 6.40 3.20 1.60 0.64
A.y= B.y= C.y= D.y=
10.如图,点A、B在反比例函数y= (x>0)的图象上,点C、D在反比例函数y= (x>0)的图象上,AC∥BD∥y轴,已知点A、B的横坐标分别为1,2,△OAC与△ABD的面积之和为 ,则k的值为( )
A.4 B.3 C.2 D.
二、填空题
11.区间测速是指检测机动车通过两个相邻测速监控点之间的路段(测速区间)上平均速度的方法.小禾一家在五一小长假期间出去游玩,发现汽车在安全行驶且不超速的条件下,在某一测速区间内行驶的平均速度与行驶时间之间是反比例函数关系,其函数图象如图所示.若小禾的爸爸安全行驶的平均速度为,则他们通过此测速区间的时间为 .
12.同学们在一次物理活动中发现:当温度不变时,某气球内的压强与气体体积成反比例函数关系,其图象如图所示,当气球内的压强大于时,气球会爆炸.为了安全,气球内气体体积应满足 .
13.科技小组为了验证某电路的电压U(V)、电流I(A)、电阻 三者之间的关系: ,测得数据如下:
100 200 220 400
2.2 1.1 1 0.55
那么,当电阻 时,电流 A.
14.若一个三角形的面积是8cm2,则其底边长y(cm)与这边上的高x(cm)之间的关系是 .
15.我们学习过反比例函数,例如,当矩形面积一定时,长a是宽b的反比例函数,其函数关系式可以写为(s为常数,s≠0).
请你仿照上例另举一个在日常生活、生产或学习中具有反比例函数关系的量的实例,并写出它的函数关系式.
实例:三角形的面积S一定时,三角形底边长y是高x的反比例函数;
函数关系式: (s为常数,s≠0).
16.如图,在平面直角坐标系中,直线与x轴交于点A,与y轴交于点C,与反比例函数在第一象限内的图象交于点B,连接.若,则的值是 .
三、计算题
17.我们把与x轴有两个不同交点的函数称为“明盟函数”,交点称为“明盟点”,两交点间的距离称为“明盟距”
(1)判断下列函数是“明盟函数”吗?如果是,请在括号里打“√”,并计算“明盟距”填在横线上,如果不是“明盟函数”则在括号里打“×”;
①( ),______;②( ),______;
(2)求出“明盟函数”的“明盟距”;
(3)“明盟函数”G:左侧的“明盟点”位于和之间(含A、B两点)时,关于t的代数式,(其中)的最小值为,求n的值.
四、解答题
18.在面积为定值的一组矩形中,当矩形的周长为24 cm时,长是宽的 2 倍.设这组矩形相邻的两边长分别为x(cm),y(cm),求 y 关于 x 的函数表达式.
19.科学课上,同学用自制密度计测量液体的密度.密度计悬浮在不同的液体中时,浸在液体中的高度h(单位:cm)是液体的密度(单位:)的反比例函数,当密度计悬浮在密度为的水中时,.
(1)求h关于的函数解析式.
(2)当密度计悬浮在另一种液体中时,,求该液体的密度.
20.某乡镇要在生活垃圾存放区建一个老年活 动中心,这样必须把1 000 m3生活垃圾运走.
(1)假如每天能运xm3,所需时间为y天,写出y与x之间的函数表达式
(2)若每辆拖拉机一天能运10 m3,则4辆这样的拖拉机要用多少天才能运完?
(3)在(2)的情况下,运了10天后,剩下的任务要用6天的时间完成,那么需要增加多少辆这样的拖拉机才能正好完成任务?
21.某学校为每个班级配备了一种可以加热的饮水机, 该饮水机的工作程序是: 加满水后, 接通电源, 饮水机自动开始加热, 每分钟水温上升 , 待加热到 , 饮水机自动停止加热, 水温开始下降, 水温 和通电时间 成反比例关系, 直至水温降至室温, 饮水机再次自动加热, 重复上述过程. 设某天水温初温和室温为 , 接通电源后,水温和时间的关系如图所示, 回答下列问题:
上午时间 作息
到校
第一节
第二节
(1) 分别求出当 和 时, 与 之间的函数表达式.
(2)求出图中 的值.
(3)该学校的作息时间如表所示, 同学们希望在上午第一节下课的时间点,即 时喝到不超过 的热水. 已知第一节下课前无人接水, 请直接写出生活委员应该在什么时间或时间段接通饮水机电源(不可以在上课时间去接通饮水机电源).
答案解析部分
1.【答案】B
【知识点】列反比例函数关系式
2.【答案】D
【知识点】反比例函数的图象;反比例函数的实际应用
3.【答案】A
【知识点】反比例函数的实际应用
4.【答案】D
【知识点】反比例函数的实际应用
5.【答案】D
【知识点】反比例函数的实际应用
6.【答案】D
【知识点】待定系数法求反比例函数解析式;反比例函数的实际应用
7.【答案】B
【知识点】反比例函数的实际应用;等腰三角形的性质;平行四边形的性质
8.【答案】B
【知识点】列反比例函数关系式
9.【答案】D
【知识点】反比例函数的实际应用
10.【答案】B
【知识点】反比例函数的实际应用
11.【答案】
【知识点】反比例函数的实际应用
12.【答案】
【知识点】反比例函数的实际应用
13.【答案】4
【知识点】反比例函数的实际应用
14.【答案】y=
【知识点】列反比例函数关系式
15.【答案】
【知识点】列反比例函数关系式
16.【答案】16
【知识点】反比例函数的实际应用
17.【答案】(1)①×;②√,
(2)4
(3)或
【知识点】列反比例函数关系式;二次函数图象与坐标轴的交点问题
18.【答案】解:设矩形的宽为a厘米,则长为2a厘米,
由题意得:
解得:a=4,
∴长方形的长为8厘米,宽为4厘米,
矩形的面积为
∴y关于x的函数表达式 .
【知识点】列反比例函数关系式;反比例函数的实际应用
19.【答案】(1).
(2)该液体的密度为.
【知识点】待定系数法求反比例函数解析式;反比例函数的实际应用
20.【答案】(1)解:每天能运x m3 ,所需时间为y天,则xy=1 000,∴y与x之间的函数表达式为y=
(2)解:∵每辆拖拉机一天能运10 m3,∴4辆拖拉机一天能运40m3,y==25,即4辆这样的拖拉机要用25天才能运完.
(3)解:在(2)的情况下,运了10天后,即运了400 m3,则还剩下600 m3,∵剩下的任务要用6天的时间完成,∴6=,解得x=100,∴共需拖拉机的数量为=10.∵10-4=6(辆),∴需要增加6辆这样的拖拉机才能正好完成任务.
【知识点】反比例函数的实际应用
21.【答案】(1)解:当0≤x≤8时,设y=kx+b,
把点(0,20)和(8,100)代入解析式得:
,
解得:k=10,b=20,
∴当0≤x≤8时,y=10x+20;
当8<x≤a时,设y=,
把点(8,100)代入解析式得:m=8×100=800,
∴当8<x≤a时,y=;
∴当0≤x≤8时,y=10x+20;
当8<x≤a时,y=;
(2)解:由图得,把y=20代入反比例函数的解析式得:
a==40.
(3)解:生活委员应该在7:20或在7:38至7:45接通饮水机电源.
【知识点】反比例函数的实际应用
21世纪教育网(www.21cnjy.com)
1 / 10
26.2实际问题与反比例函数
一、单选题
1.已知甲、乙两地相距40米,汽车从甲地匀速行驶到乙地,则汽车行驶时间t(单位:小时)关于行驶速度v(单位:千米/小时)的函数关系式是( )
A.t=40v B. C. D.
2.A,B两城间的距离为15千米,一人行路的平均速度每小时不少于3千米,也不多于5千米,则表示此人由A到B的行路速度x(千米/小时)与所用时间y(小时)的关系y= 的函数图象是( )
A. B.
C. D.
3.在一个密闭的容器内装有一定质量的某种气体,当它的容积V改变时,气体的密度也随之改变,与V之间在一定范围内满足,如图所示.当为时,V的值是( )
A. B. C. D.
4.在一个可以改变容积的密闭容器内,装有质量为m 的气体,当改变容积V时,气体的密度ρ也随之改变,与V在一定范围内满足,它的图象如的质量m为( )
A. B. C. D.
5.工程队铺设某段公路效率是v(单位:/天)和铺设时间t(单位:天)之间函数图象是( )
A. B.
C. D.
6.如图1是一个亮度可调节的台灯,其灯光亮度的改变,可以通过调节总电阻控制电流的变化来实现.如图2是该台灯的电流与电阻成反比例函数的图象,该图象经过点.根据图象可知,下列说法正确的是( )
A.当时,
B.I与R的函数关系式是
C.当时,
D.当时,I的取值范围是
7.如图,点在轴的正半轴上,点在第一象限,,反比例函数的图像经过点,反比例函数的图像经过点.若,则的值为( )
A.2 B.3 C.4 D.5
8.已知一个矩形的面积为20,若设长为a,宽为b,则能大致反映a与b之间函数关系的图象为( )
A. B.
C. D.
9.在做拉面的过程中渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(mm)与面条的粗细s(mm )(横截面积)的对应数据如下表.根据表中数据,可得y关于s的函数表达式为( )
面条的总长度y(mm) 100 200 400 800 2000
面条的粗细s(mm2) 12.80 6.40 3.20 1.60 0.64
A.y= B.y= C.y= D.y=
10.如图,点A、B在反比例函数y= (x>0)的图象上,点C、D在反比例函数y= (x>0)的图象上,AC∥BD∥y轴,已知点A、B的横坐标分别为1,2,△OAC与△ABD的面积之和为 ,则k的值为( )
A.4 B.3 C.2 D.
二、填空题
11.区间测速是指检测机动车通过两个相邻测速监控点之间的路段(测速区间)上平均速度的方法.小禾一家在五一小长假期间出去游玩,发现汽车在安全行驶且不超速的条件下,在某一测速区间内行驶的平均速度与行驶时间之间是反比例函数关系,其函数图象如图所示.若小禾的爸爸安全行驶的平均速度为,则他们通过此测速区间的时间为 .
12.同学们在一次物理活动中发现:当温度不变时,某气球内的压强与气体体积成反比例函数关系,其图象如图所示,当气球内的压强大于时,气球会爆炸.为了安全,气球内气体体积应满足 .
13.科技小组为了验证某电路的电压U(V)、电流I(A)、电阻 三者之间的关系: ,测得数据如下:
100 200 220 400
2.2 1.1 1 0.55
那么,当电阻 时,电流 A.
14.若一个三角形的面积是8cm2,则其底边长y(cm)与这边上的高x(cm)之间的关系是 .
15.我们学习过反比例函数,例如,当矩形面积一定时,长a是宽b的反比例函数,其函数关系式可以写为(s为常数,s≠0).
请你仿照上例另举一个在日常生活、生产或学习中具有反比例函数关系的量的实例,并写出它的函数关系式.
实例:三角形的面积S一定时,三角形底边长y是高x的反比例函数;
函数关系式: (s为常数,s≠0).
16.如图,在平面直角坐标系中,直线与x轴交于点A,与y轴交于点C,与反比例函数在第一象限内的图象交于点B,连接.若,则的值是 .
三、计算题
17.我们把与x轴有两个不同交点的函数称为“明盟函数”,交点称为“明盟点”,两交点间的距离称为“明盟距”
(1)判断下列函数是“明盟函数”吗?如果是,请在括号里打“√”,并计算“明盟距”填在横线上,如果不是“明盟函数”则在括号里打“×”;
①( ),______;②( ),______;
(2)求出“明盟函数”的“明盟距”;
(3)“明盟函数”G:左侧的“明盟点”位于和之间(含A、B两点)时,关于t的代数式,(其中)的最小值为,求n的值.
四、解答题
18.在面积为定值的一组矩形中,当矩形的周长为24 cm时,长是宽的 2 倍.设这组矩形相邻的两边长分别为x(cm),y(cm),求 y 关于 x 的函数表达式.
19.科学课上,同学用自制密度计测量液体的密度.密度计悬浮在不同的液体中时,浸在液体中的高度h(单位:cm)是液体的密度(单位:)的反比例函数,当密度计悬浮在密度为的水中时,.
(1)求h关于的函数解析式.
(2)当密度计悬浮在另一种液体中时,,求该液体的密度.
20.某乡镇要在生活垃圾存放区建一个老年活 动中心,这样必须把1 000 m3生活垃圾运走.
(1)假如每天能运xm3,所需时间为y天,写出y与x之间的函数表达式
(2)若每辆拖拉机一天能运10 m3,则4辆这样的拖拉机要用多少天才能运完?
(3)在(2)的情况下,运了10天后,剩下的任务要用6天的时间完成,那么需要增加多少辆这样的拖拉机才能正好完成任务?
21.某学校为每个班级配备了一种可以加热的饮水机, 该饮水机的工作程序是: 加满水后, 接通电源, 饮水机自动开始加热, 每分钟水温上升 , 待加热到 , 饮水机自动停止加热, 水温开始下降, 水温 和通电时间 成反比例关系, 直至水温降至室温, 饮水机再次自动加热, 重复上述过程. 设某天水温初温和室温为 , 接通电源后,水温和时间的关系如图所示, 回答下列问题:
上午时间 作息
到校
第一节
第二节
(1) 分别求出当 和 时, 与 之间的函数表达式.
(2)求出图中 的值.
(3)该学校的作息时间如表所示, 同学们希望在上午第一节下课的时间点,即 时喝到不超过 的热水. 已知第一节下课前无人接水, 请直接写出生活委员应该在什么时间或时间段接通饮水机电源(不可以在上课时间去接通饮水机电源).
答案解析部分
1.【答案】B
【知识点】列反比例函数关系式
2.【答案】D
【知识点】反比例函数的图象;反比例函数的实际应用
3.【答案】A
【知识点】反比例函数的实际应用
4.【答案】D
【知识点】反比例函数的实际应用
5.【答案】D
【知识点】反比例函数的实际应用
6.【答案】D
【知识点】待定系数法求反比例函数解析式;反比例函数的实际应用
7.【答案】B
【知识点】反比例函数的实际应用;等腰三角形的性质;平行四边形的性质
8.【答案】B
【知识点】列反比例函数关系式
9.【答案】D
【知识点】反比例函数的实际应用
10.【答案】B
【知识点】反比例函数的实际应用
11.【答案】
【知识点】反比例函数的实际应用
12.【答案】
【知识点】反比例函数的实际应用
13.【答案】4
【知识点】反比例函数的实际应用
14.【答案】y=
【知识点】列反比例函数关系式
15.【答案】
【知识点】列反比例函数关系式
16.【答案】16
【知识点】反比例函数的实际应用
17.【答案】(1)①×;②√,
(2)4
(3)或
【知识点】列反比例函数关系式;二次函数图象与坐标轴的交点问题
18.【答案】解:设矩形的宽为a厘米,则长为2a厘米,
由题意得:
解得:a=4,
∴长方形的长为8厘米,宽为4厘米,
矩形的面积为
∴y关于x的函数表达式 .
【知识点】列反比例函数关系式;反比例函数的实际应用
19.【答案】(1).
(2)该液体的密度为.
【知识点】待定系数法求反比例函数解析式;反比例函数的实际应用
20.【答案】(1)解:每天能运x m3 ,所需时间为y天,则xy=1 000,∴y与x之间的函数表达式为y=
(2)解:∵每辆拖拉机一天能运10 m3,∴4辆拖拉机一天能运40m3,y==25,即4辆这样的拖拉机要用25天才能运完.
(3)解:在(2)的情况下,运了10天后,即运了400 m3,则还剩下600 m3,∵剩下的任务要用6天的时间完成,∴6=,解得x=100,∴共需拖拉机的数量为=10.∵10-4=6(辆),∴需要增加6辆这样的拖拉机才能正好完成任务.
【知识点】反比例函数的实际应用
21.【答案】(1)解:当0≤x≤8时,设y=kx+b,
把点(0,20)和(8,100)代入解析式得:
,
解得:k=10,b=20,
∴当0≤x≤8时,y=10x+20;
当8<x≤a时,设y=,
把点(8,100)代入解析式得:m=8×100=800,
∴当8<x≤a时,y=;
∴当0≤x≤8时,y=10x+20;
当8<x≤a时,y=;
(2)解:由图得,把y=20代入反比例函数的解析式得:
a==40.
(3)解:生活委员应该在7:20或在7:38至7:45接通饮水机电源.
【知识点】反比例函数的实际应用
21世纪教育网(www.21cnjy.com)
1 / 10
