27.1图形的相似(含答案)
图片预览

文档简介
中小学教育资源及组卷应用平台
27.1图形的相似
一、单选题
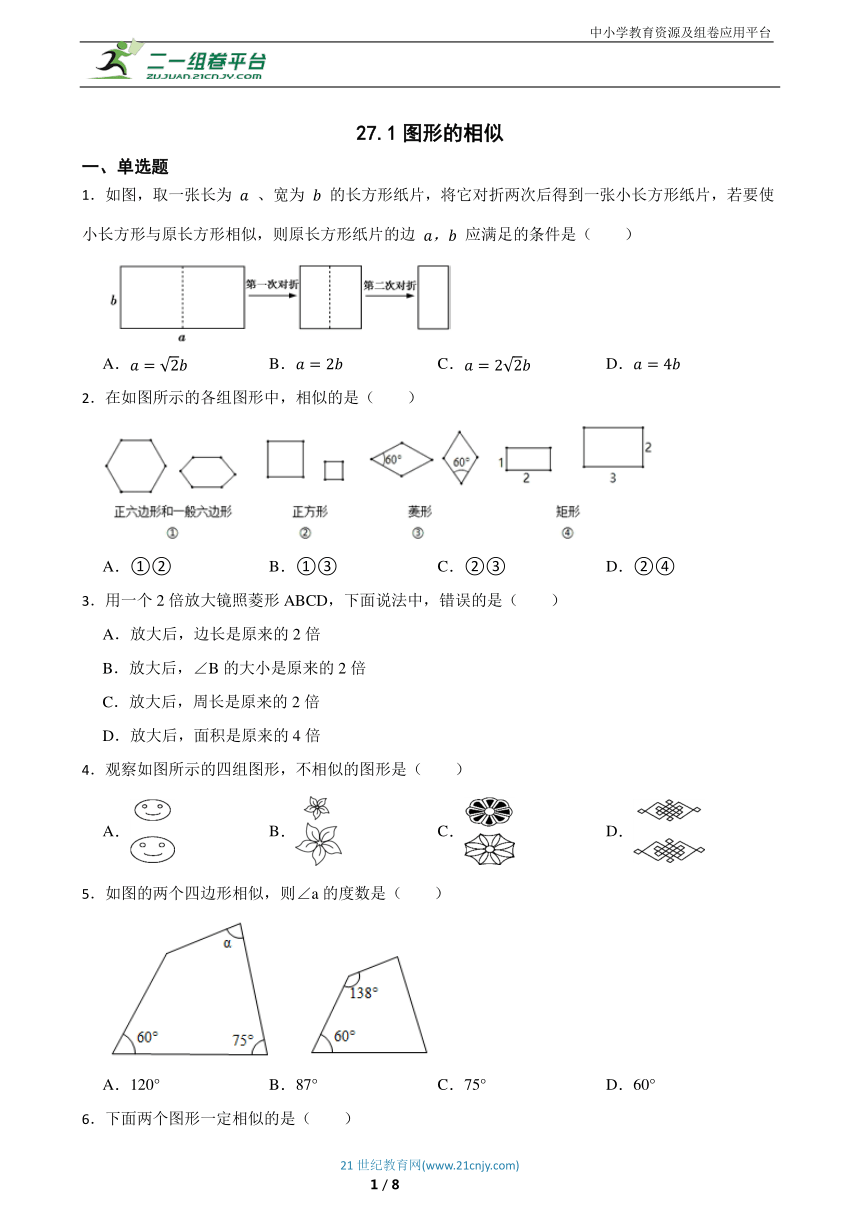
1.如图,取一张长为 、宽为 的长方形纸片,将它对折两次后得到一张小长方形纸片,若要使小长方形与原长方形相似,则原长方形纸片的边 应满足的条件是( )
A. B. C. D.
2.在如图所示的各组图形中,相似的是( )
A.①② B.①③ C.②③ D.②④
3.用一个2倍放大镜照菱形ABCD,下面说法中,错误的是( )
A.放大后,边长是原来的2倍
B.放大后,∠B的大小是原来的2倍
C.放大后,周长是原来的2倍
D.放大后,面积是原来的4倍
4.观察如图所示的四组图形,不相似的图形是( )
A. B. C. D.
5.如图的两个四边形相似,则∠a的度数是( )
A.120° B.87° C.75° D.60°
6.下面两个图形一定相似的是( )
A.两个等腰三角形 B.矩形
C.菱形 D.正方形
7.如图,把一个长方形划分成三个全等的小长方形,若要使每一个小长方形与原长方形相似,则原长方形长和宽之比为( )
A.3:1 B.:1 C.2:1 D.:1
8.下列两个图形一定相似的是( )
A.矩形
B.菱形
C.直角三角形
D.有一个内角为 的等腰三角形
9.下列图形一定是相似图形的是( )
A.两个矩形 B.两个正方形
C.两个直角三角形 D.两个等腰三角形
10.如图, 点P是平行四边形内部一点, 过P分别作和的平行线交平行四边 形的四边于. 连结分别交于M和N. 若四边形四边形,且四边形的面积是四边形的3倍. 下列选项正确的是( )
A. B. C. D.
二、填空题
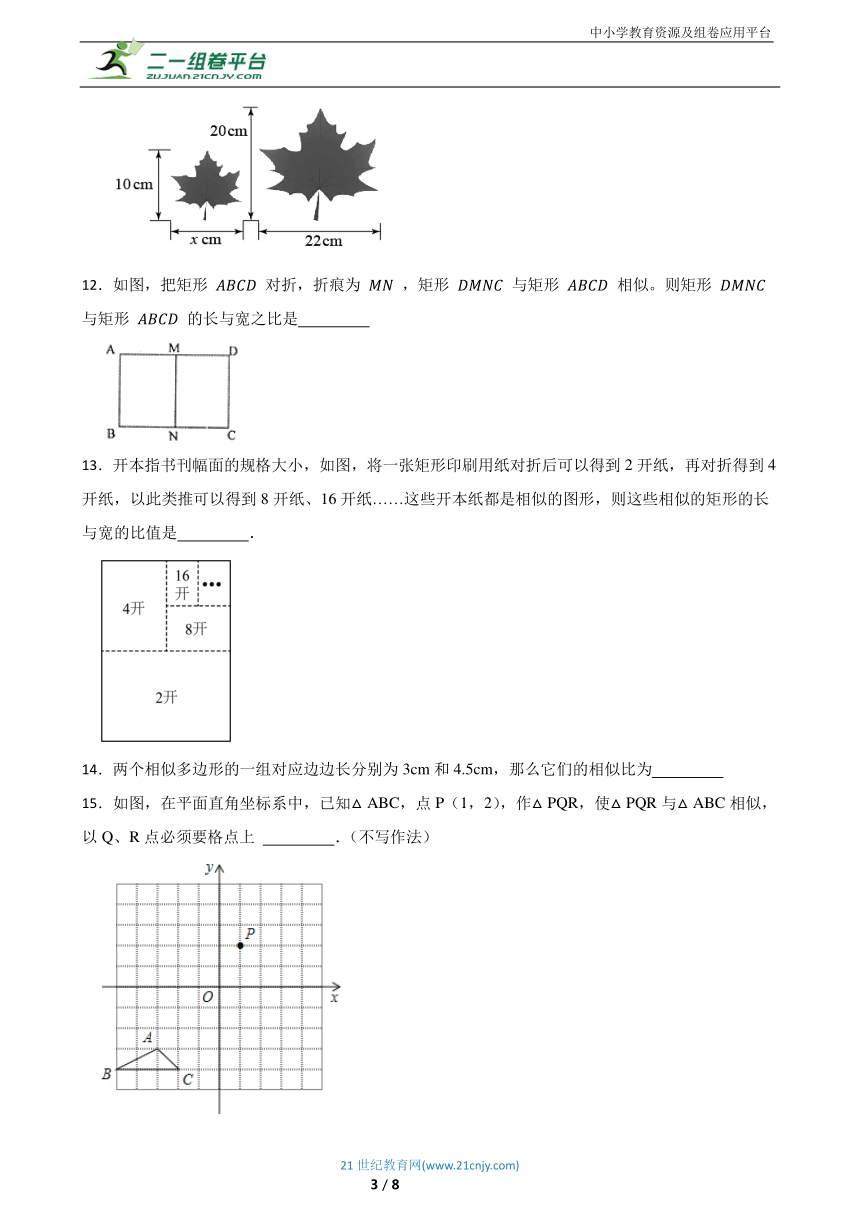
11.秋天红透的枫叶,总能牵动人们无尽的思绪,所以诗人杜牧说:“停车坐爱枫林晚,霜叶红于二月花”如图是两片形状相同的枫叶图案,则x的值为 .
12.如图,把矩形 对折,折痕为 ,矩形 与矩形 相似。则矩形 与矩形 的长与宽之比是
13.开本指书刊幅面的规格大小,如图,将一张矩形印刷用纸对折后可以得到2开纸,再对折得到4开纸,以此类推可以得到8开纸、16开纸……这些开本纸都是相似的图形,则这些相似的矩形的长与宽的比值是 .
14.两个相似多边形的一组对应边边长分别为3cm和4.5cm,那么它们的相似比为
15.如图,在平面直角坐标系中,已知△ABC,点P(1,2),作△PQR,使△PQR与△ABC相似,以Q、R点必须要格点上 .(不写作法)
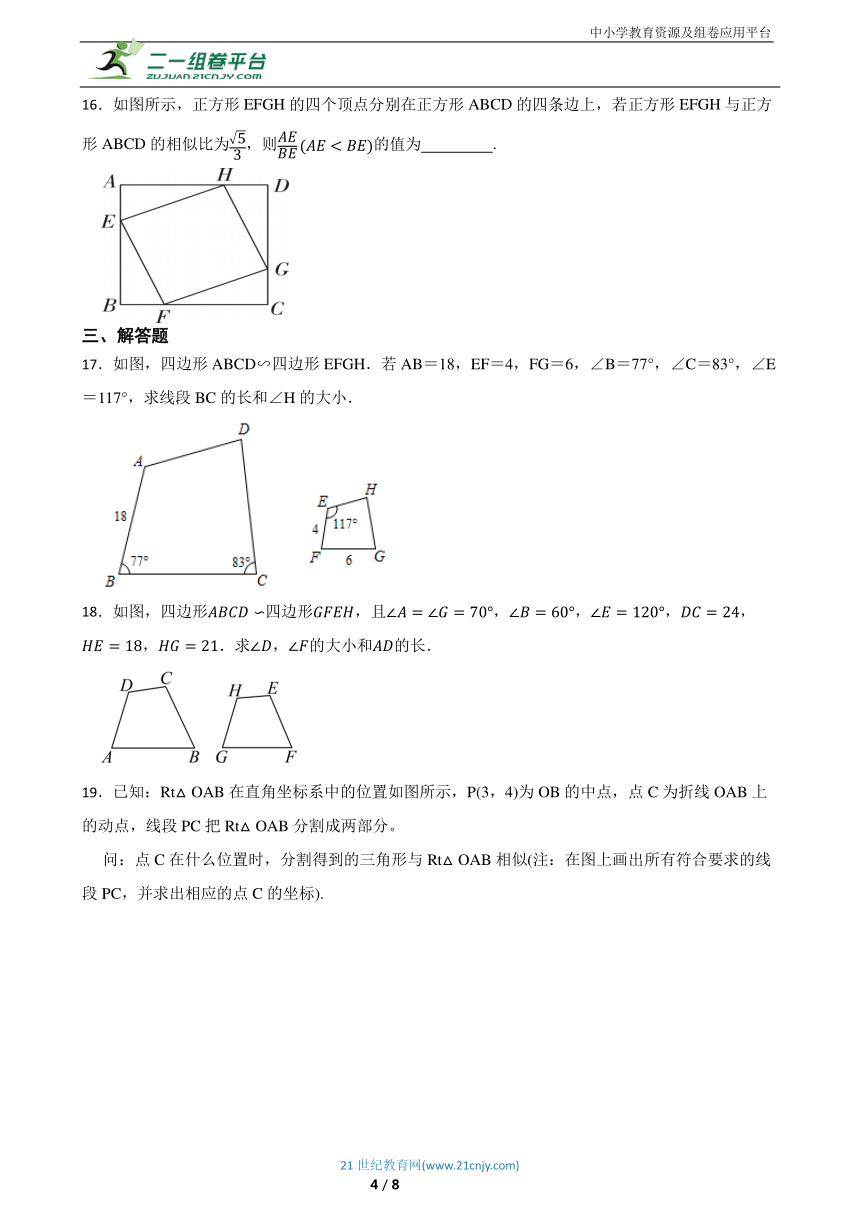
16.如图所示,正方形EFGH的四个顶点分别在正方形ABCD的四条边上,若正方形EFGH与正方形ABCD的相似比为,则的值为 .
三、解答题
17.如图,四边形ABCD∽四边形EFGH.若AB=18,EF=4,FG=6,∠B=77°,∠C=83°,∠E=117°,求线段BC的长和∠H的大小.
18.如图,四边形四边形,且,,,,,.求,的大小和的长.
19.已知:Rt△OAB在直角坐标系中的位置如图所示,P(3,4)为OB的中点,点C为折线OAB上的动点,线段PC把Rt△OAB分割成两部分。
问:点C在什么位置时,分割得到的三角形与Rt△OAB相似(注:在图上画出所有符合要求的线段PC,并求出相应的点C的坐标).
20.如图所示,系列矩形纸张的规格特征是:①各矩形纸张都相似;②纸对裁后可以得到两张纸,纸对裁后可以得到两张纸,纸对裁后可以得到两张纸.
(1)填空:纸面积是纸面积的 倍,纸周长是纸周长的 倍.
(2)根据系列纸张的规格特征,求出该系列纸张的长与宽(长大于宽)之比.
(3)设1张纸张的重量为克,试求出1张纸张的质量.(用含的代数式表示)
答案解析部分
1.【答案】B
【知识点】相似多边形
2.【答案】C
【知识点】图形的相似
3.【答案】B
【知识点】菱形的性质;相似多边形
4.【答案】C
【知识点】图形的相似
5.【答案】B
【知识点】相似多边形
6.【答案】D
【知识点】图形的相似
7.【答案】B
【知识点】相似多边形
8.【答案】D
【知识点】图形的相似
9.【答案】B
【知识点】图形的相似
10.【答案】D
【知识点】三角形全等及其性质;平行四边形的判定与性质;相似多边形
11.【答案】11
【知识点】相似多边形
12.【答案】
【知识点】相似多边形
13.【答案】
【知识点】相似多边形
14.【答案】
【知识点】相似多边形
15.【答案】略
【知识点】作图﹣相似变换
16.【答案】
【知识点】勾股定理;正方形的性质;相似多边形;三角形全等的判定-ASA
17.【答案】解:BC=27,∠H=83°
【知识点】相似多边形
18.【答案】,,.
【知识点】相似多边形
19.【答案】解:过P作PC1⊥OA,垂足是C1,
则△OC1P∽△OAB.
点C1坐标是(3,0).
过P作PC2⊥AB,垂足是C2,
则△PC2B∽△OAB.
点C2坐标是(6,4).
过P作PC3⊥OB,垂足是P(如图),
则△C3PB∽△OAB,
∴ .
易知OB=10,BP=5,BA=8,
∴BC3= ,AC3=8﹣ = .
∴C3(6, ).
符合要求的点C有三个,其连线段分别是PC1,PC2,PC3(如图).
故答案是:(3,0)或(6,4)或(6, ).
【知识点】坐标与图形性质;作图﹣相似变换
20.【答案】(1)2;2
(2)解:设A1的长宽为m、n,则A2的长宽为n、,
∵两个矩形相似,
∴,
∴;
(3)解:由(1)可得对裁后的矩形重量是对裁前的,即克.
【知识点】轴对称的性质;相似多边形
21世纪教育网(www.21cnjy.com)
1 / 8
27.1图形的相似
一、单选题
1.如图,取一张长为 、宽为 的长方形纸片,将它对折两次后得到一张小长方形纸片,若要使小长方形与原长方形相似,则原长方形纸片的边 应满足的条件是( )
A. B. C. D.
2.在如图所示的各组图形中,相似的是( )
A.①② B.①③ C.②③ D.②④
3.用一个2倍放大镜照菱形ABCD,下面说法中,错误的是( )
A.放大后,边长是原来的2倍
B.放大后,∠B的大小是原来的2倍
C.放大后,周长是原来的2倍
D.放大后,面积是原来的4倍
4.观察如图所示的四组图形,不相似的图形是( )
A. B. C. D.
5.如图的两个四边形相似,则∠a的度数是( )
A.120° B.87° C.75° D.60°
6.下面两个图形一定相似的是( )
A.两个等腰三角形 B.矩形
C.菱形 D.正方形
7.如图,把一个长方形划分成三个全等的小长方形,若要使每一个小长方形与原长方形相似,则原长方形长和宽之比为( )
A.3:1 B.:1 C.2:1 D.:1
8.下列两个图形一定相似的是( )
A.矩形
B.菱形
C.直角三角形
D.有一个内角为 的等腰三角形
9.下列图形一定是相似图形的是( )
A.两个矩形 B.两个正方形
C.两个直角三角形 D.两个等腰三角形
10.如图, 点P是平行四边形内部一点, 过P分别作和的平行线交平行四边 形的四边于. 连结分别交于M和N. 若四边形四边形,且四边形的面积是四边形的3倍. 下列选项正确的是( )
A. B. C. D.
二、填空题
11.秋天红透的枫叶,总能牵动人们无尽的思绪,所以诗人杜牧说:“停车坐爱枫林晚,霜叶红于二月花”如图是两片形状相同的枫叶图案,则x的值为 .
12.如图,把矩形 对折,折痕为 ,矩形 与矩形 相似。则矩形 与矩形 的长与宽之比是
13.开本指书刊幅面的规格大小,如图,将一张矩形印刷用纸对折后可以得到2开纸,再对折得到4开纸,以此类推可以得到8开纸、16开纸……这些开本纸都是相似的图形,则这些相似的矩形的长与宽的比值是 .
14.两个相似多边形的一组对应边边长分别为3cm和4.5cm,那么它们的相似比为
15.如图,在平面直角坐标系中,已知△ABC,点P(1,2),作△PQR,使△PQR与△ABC相似,以Q、R点必须要格点上 .(不写作法)
16.如图所示,正方形EFGH的四个顶点分别在正方形ABCD的四条边上,若正方形EFGH与正方形ABCD的相似比为,则的值为 .
三、解答题
17.如图,四边形ABCD∽四边形EFGH.若AB=18,EF=4,FG=6,∠B=77°,∠C=83°,∠E=117°,求线段BC的长和∠H的大小.
18.如图,四边形四边形,且,,,,,.求,的大小和的长.
19.已知:Rt△OAB在直角坐标系中的位置如图所示,P(3,4)为OB的中点,点C为折线OAB上的动点,线段PC把Rt△OAB分割成两部分。
问:点C在什么位置时,分割得到的三角形与Rt△OAB相似(注:在图上画出所有符合要求的线段PC,并求出相应的点C的坐标).
20.如图所示,系列矩形纸张的规格特征是:①各矩形纸张都相似;②纸对裁后可以得到两张纸,纸对裁后可以得到两张纸,纸对裁后可以得到两张纸.
(1)填空:纸面积是纸面积的 倍,纸周长是纸周长的 倍.
(2)根据系列纸张的规格特征,求出该系列纸张的长与宽(长大于宽)之比.
(3)设1张纸张的重量为克,试求出1张纸张的质量.(用含的代数式表示)
答案解析部分
1.【答案】B
【知识点】相似多边形
2.【答案】C
【知识点】图形的相似
3.【答案】B
【知识点】菱形的性质;相似多边形
4.【答案】C
【知识点】图形的相似
5.【答案】B
【知识点】相似多边形
6.【答案】D
【知识点】图形的相似
7.【答案】B
【知识点】相似多边形
8.【答案】D
【知识点】图形的相似
9.【答案】B
【知识点】图形的相似
10.【答案】D
【知识点】三角形全等及其性质;平行四边形的判定与性质;相似多边形
11.【答案】11
【知识点】相似多边形
12.【答案】
【知识点】相似多边形
13.【答案】
【知识点】相似多边形
14.【答案】
【知识点】相似多边形
15.【答案】略
【知识点】作图﹣相似变换
16.【答案】
【知识点】勾股定理;正方形的性质;相似多边形;三角形全等的判定-ASA
17.【答案】解:BC=27,∠H=83°
【知识点】相似多边形
18.【答案】,,.
【知识点】相似多边形
19.【答案】解:过P作PC1⊥OA,垂足是C1,
则△OC1P∽△OAB.
点C1坐标是(3,0).
过P作PC2⊥AB,垂足是C2,
则△PC2B∽△OAB.
点C2坐标是(6,4).
过P作PC3⊥OB,垂足是P(如图),
则△C3PB∽△OAB,
∴ .
易知OB=10,BP=5,BA=8,
∴BC3= ,AC3=8﹣ = .
∴C3(6, ).
符合要求的点C有三个,其连线段分别是PC1,PC2,PC3(如图).
故答案是:(3,0)或(6,4)或(6, ).
【知识点】坐标与图形性质;作图﹣相似变换
20.【答案】(1)2;2
(2)解:设A1的长宽为m、n,则A2的长宽为n、,
∵两个矩形相似,
∴,
∴;
(3)解:由(1)可得对裁后的矩形重量是对裁前的,即克.
【知识点】轴对称的性质;相似多边形
21世纪教育网(www.21cnjy.com)
1 / 8
