27.2.3相似三角形的应用举例(含答案)
文档属性
| 名称 | 27.2.3相似三角形的应用举例(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 891.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-27 14:03:11 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
27.2。3相似三角形的应用举例
一、填空题
1.如图,小明用长为3m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的顶端C、A与O点在一条直线上,则根据图中数据可得旗杆AB的高为 m.
2.如图,是小明设计用手电来测量某古城墙高度的示意图,点处放一水平的平面镜,光线从点出发经平面镜反射后刚好射到古城墙的顶端处,已知,且测得,那么该古城墙的高度是 .
3.如图①是用杠杆撬石头的示意图,当用力压杠杆时,杠杆绕着支点转动,另一端会向上翘起,石头就被翘动了.在图②中,杠杆的端被向上翘起的距离,动力臂与阻力臂满足(与相交于点),要把这块石头翘起,至少要将杠杆的点向下压 .
4.如图,网高为0.8米,击球点到网的水平距离为3米,小明在打网球时,要使球恰好能打过网,且落点恰好在离网4米的位置上,则球拍击球的高度h为 米.
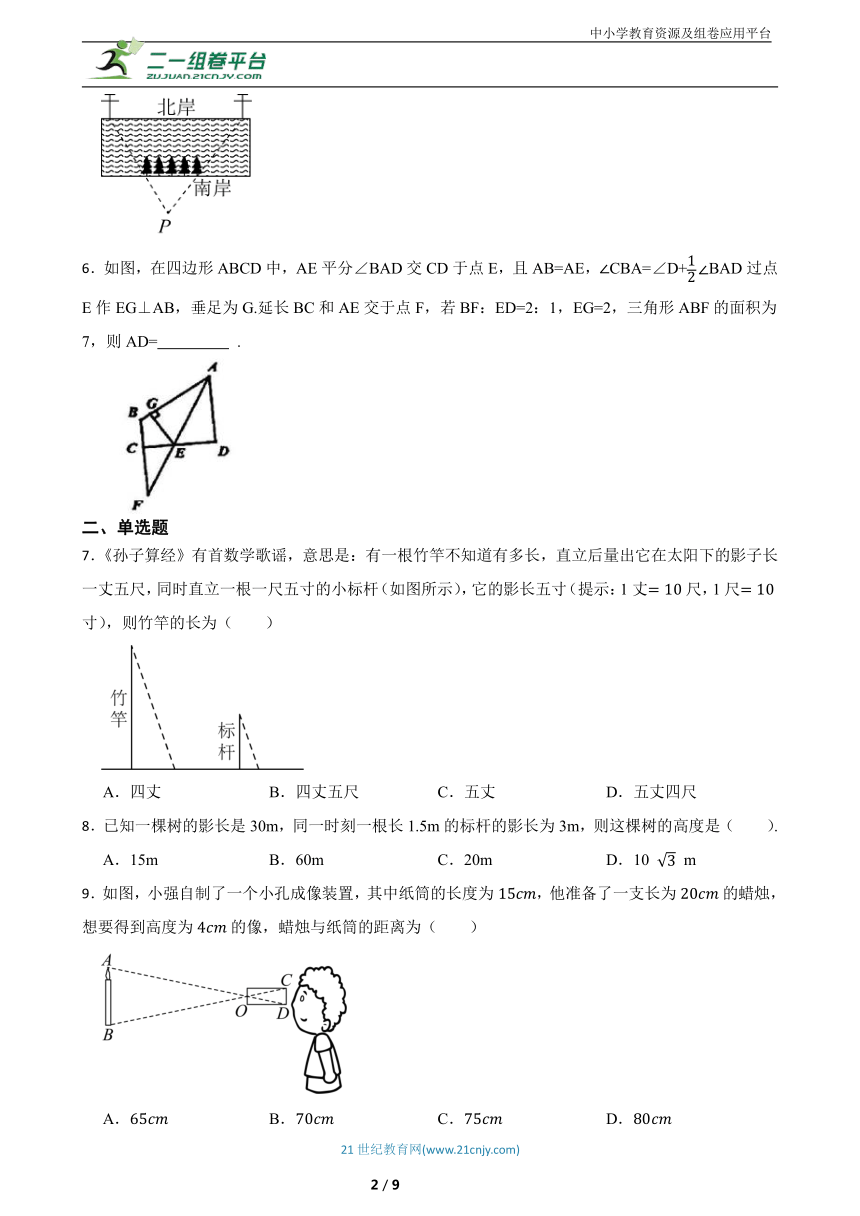
5.如图所示,一条河流的两岸互相平行,沿南岸有一排大树,每隔4米一棵,沿北岸有一排电线杆,每两根电线杆之间的距离为80米,一同学站在距南岸9米的点P处,正好北岸相邻的两根电线杆被南岸的5棵树遮挡住,那么这条河流的宽度是 米.
6.如图,在四边形ABCD中,AE平分∠BAD交CD于点E,且AB=AE,CBA=∠D+BAD过点E作EG⊥AB,垂足为G.延长BC和AE交于点F,若BF:ED=2:1,EG=2,三角形ABF的面积为7,则AD= .
二、单选题
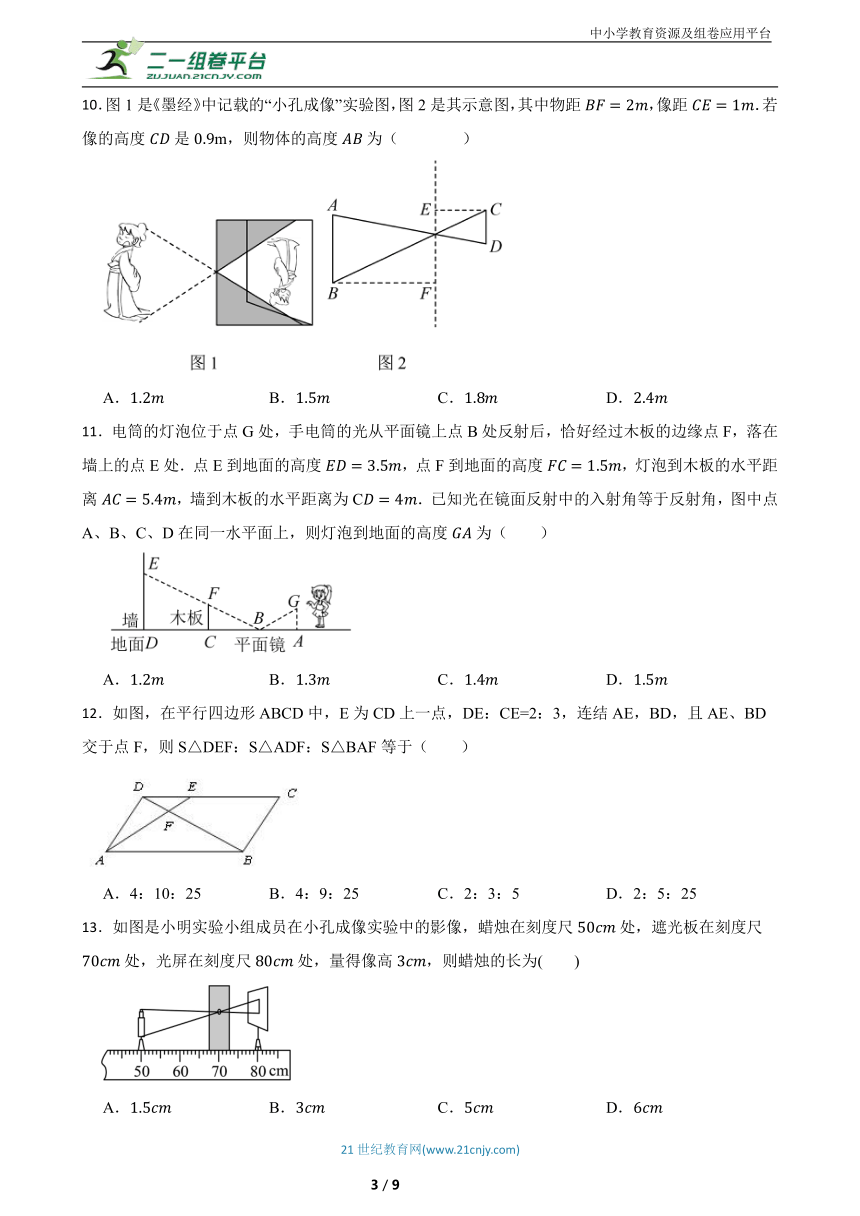
7.《孙子算经》有首数学歌谣,意思是:有一根竹竿不知道有多长,直立后量出它在太阳下的影子长一丈五尺,同时直立一根一尺五寸的小标杆(如图所示),它的影长五寸(提示:1丈尺,1尺寸),则竹竿的长为( )
A.四丈 B.四丈五尺 C.五丈 D.五丈四尺
8.已知一棵树的影长是30m,同一时刻一根长1.5m的标杆的影长为3m,则这棵树的高度是( ).
A.15m B.60m C.20m D.10 m
9.如图,小强自制了一个小孔成像装置,其中纸筒的长度为,他准备了一支长为的蜡烛,想要得到高度为的像,蜡烛与纸筒的距离为( )
A. B. C. D.
10.图1是《墨经》中记载的“小孔成像”实验图,图2是其示意图,其中物距,像距.若像的高度是m,则物体的高度为( )
A. B. C. D.
11.电筒的灯泡位于点G处,手电筒的光从平面镜上点B处反射后,恰好经过木板的边缘点F,落在墙上的点E处.点E到地面的高度,点F到地面的高度,灯泡到木板的水平距离,墙到木板的水平距离为C.已知光在镜面反射中的入射角等于反射角,图中点A、B、C、D在同一水平面上,则灯泡到地面的高度为( )
A. B. C. D.
12.如图,在平行四边形ABCD中,E为CD上一点,DE:CE=2:3,连结AE,BD,且AE、BD交于点F,则S△DEF:S△ADF:S△BAF等于( )
A.4:10:25 B.4:9:25 C.2:3:5 D.2:5:25
13.如图是小明实验小组成员在小孔成像实验中的影像,蜡烛在刻度尺处,遮光板在刻度尺处,光屏在刻度尺处,量得像高,则蜡烛的长为( )
A. B. C. D.
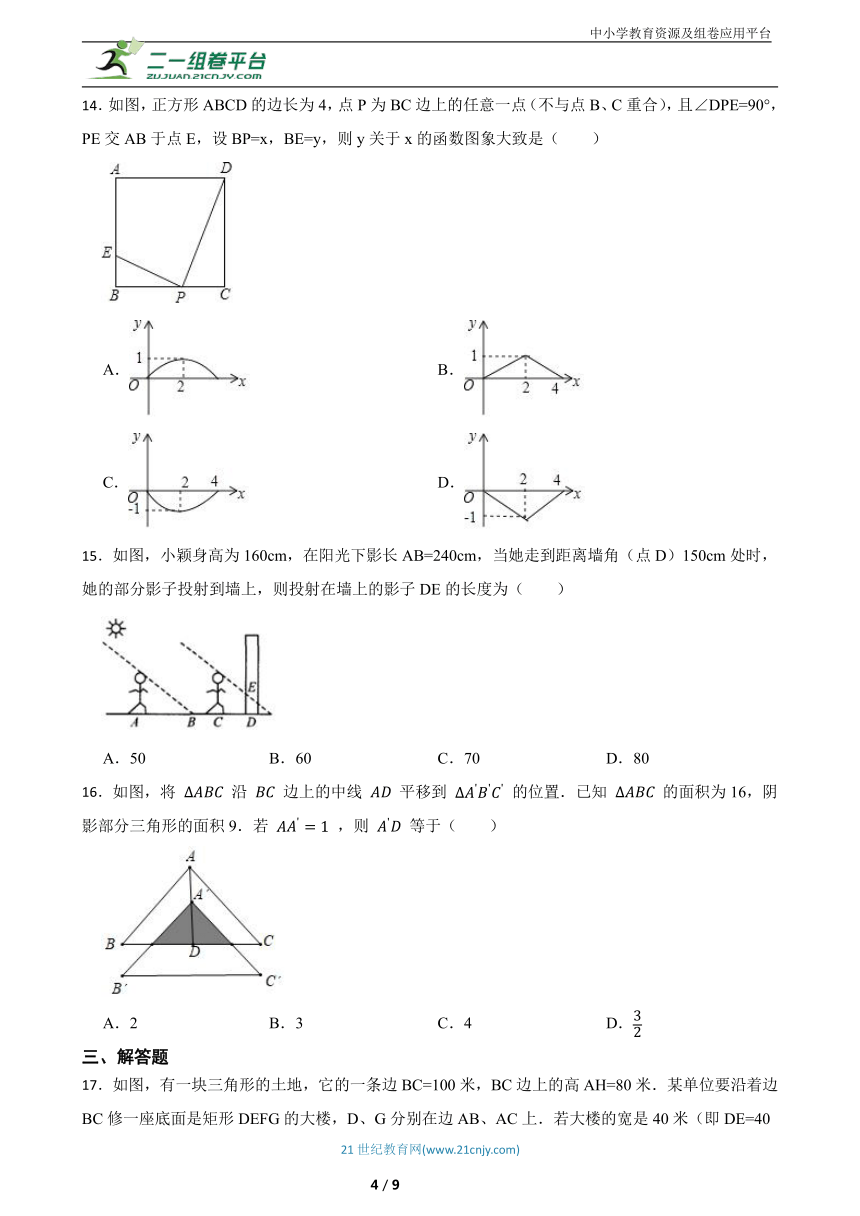
14.如图,正方形ABCD的边长为4,点P为BC边上的任意一点(不与点B、C重合),且∠DPE=90°,PE交AB于点E,设BP=x,BE=y,则y关于x的函数图象大致是( )
A. B.
C. D.
15.如图,小颖身高为160cm,在阳光下影长AB=240cm,当她走到距离墙角(点D)150cm处时,她的部分影子投射到墙上,则投射在墙上的影子DE的长度为( )
A.50 B.60 C.70 D.80
16.如图,将 沿 边上的中线 平移到 的位置.已知 的面积为16,阴影部分三角形的面积9.若 ,则 等于( )
A.2 B.3 C.4 D.
三、解答题
17.如图,有一块三角形的土地,它的一条边BC=100米,BC边上的高AH=80米.某单位要沿着边BC修一座底面是矩形DEFG的大楼,D、G分别在边AB、AC上.若大楼的宽是40米(即DE=40米),求这个矩形的面积.
18.小聪和他的同学利用影长测量旗杆高度(如图),当1m长的直立竹竿的影长为1.5m时,测量旗杆落在地上的影长为21m,落在墙上的影长为2m.求旗杆的高度.
19.在一次数学活动课上,老师让同学们到操场上测量旗杆的高度,然后回来交流各自的测量方法.小芳的测量方法是:拿一根高3.5米的竹竿直立在离旗杆27米的C处(如图),然后沿BC方向走到D处,这时目测旗杆顶部A与竹竿顶部E恰好在同一直线上,又测得C、D两点的距离为3米,小芳的目高为1.5米,这样便可知道旗杆的高.你认为这种测量方法是否可行?请说明理由.
20.如图,在△ABC中,AB=4cm,BC=8cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P、Q分别从A、B同时出发,经几秒后,点P、B、Q构成的三角形△PBQ与△ABC相似
四、计算题
21.为了测量学校旗杆的高度AB,数学兴趣小组带着标杆和皮尺来到操场进行测量,测 量方案如下:如图,首先,小红在C处放置一平面镜,她从点C沿BC后退,当退行1.8米到D处时,恰好在镜子中看到旗杆顶点A的像,此时测得小红眼睛到地面的距离ED为1.5米;然后,小明在F 处竖立了一根高1.6米的标杆FG,发现地面上的点H、标杆顶点G和旗杆顶点A在一条直线上,此时测得FH为2.4米,DF为3.3米,已知AB⊥BH,ED⊥BH,GF⊥BH,点B、C、D、F、H在一条直线上.
(1)直接写出 ;
(2)请根据以上所测数据,计算学校旗杆AB的高度.
22.学习相似三角形相关知识后,善于思考的小明和小颖两位同学想通过所学计算桥的长.如图,该桥两侧河岸平行,他们在河的对岸选定一个目标作为点,再在河岸的这一边选出点和点,分别在、的延长线上取点、,使得.经测量,米,米,且点到河岸的距离为60米.已知于点,请你根据提供的数据,帮助他们计算桥的长度.
23.课本中有一道作业题:
有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.问加工成的正方形零件的边长是多少mm?
小颖解得此题的答案为48mm,小颖善于反思,她又提出了如下的问题.
(1)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少mm?请你计算.
(2)如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.
答案解析部分
1.【答案】9
【知识点】相似三角形的应用
2.【答案】8
【知识点】相似三角形的应用
3.【答案】
【知识点】相似三角形的应用
4.【答案】1.4
【知识点】相似三角形的应用
5.【答案】36
【知识点】相似三角形的应用
6.【答案】
【知识点】角平分线的性质;相似三角形的判定与性质;相似三角形的应用;角平分线的判定
7.【答案】B
【知识点】相似三角形的应用
8.【答案】A
【知识点】相似三角形的应用
9.【答案】C
【知识点】相似三角形的应用
10.【答案】C
【知识点】相似三角形的应用
11.【答案】A
【知识点】相似三角形的应用
12.【答案】B
【知识点】平行四边形的性质;相似三角形的应用
13.【答案】D
【知识点】相似三角形的判定与性质;相似三角形的应用
14.【答案】A
【知识点】函数的图象;相似三角形的应用
15.【答案】B
【知识点】相似三角形的应用
16.【答案】B
【知识点】相似三角形的应用
17.【答案】解答:由已知得,DG∥BC∴△ADG∽△ABC,∵AH⊥BC∴AH⊥DG于点M,且AM=AH-MH=80-40=40(m) = ,即DG= =50(m),∴S矩形DEFG=DE×DG=2000(m2).
【知识点】相似三角形的应用
18.【答案】解:如图,CD=2m,BD=21m,
∵,
∴DE=1.5CD=3,
∵,
∴AB==16(m).
答:旗杆的高度为16m.
【知识点】相似三角形的应用
19.【答案】这种测量方法可行,旗杆的高为21.5米.
【知识点】相似三角形的判定与性质;相似三角形的应用
20.【答案】解:设经过t秒后,△PBQ与△ABC相似,
∵点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,
∴AP=t,BQ=2t,
∵AB=4,BC=8,
∴BP=AB-AP=4-t,
①当△PBQ∽△ABC时,
∴,
即,
解得:t=2;
②当△PBQ∽△CBA时,
∴,
即,
解得:t=;
综上所述:经过2秒或秒,△PBQ与△ABC相似.
【知识点】相似三角形的性质;相似三角形的应用
21.【答案】(1);(2)学校旗杆AB的高度为25米.
【知识点】相似三角形的应用
22.【答案】桥的长度为90米
【知识点】相似三角形的应用
23.【答案】(1)mm,mm;(2)PN=60mm,mm.
【知识点】相似三角形的应用
21世纪教育网(www.21cnjy.com)
2 / 9
27.2。3相似三角形的应用举例
一、填空题
1.如图,小明用长为3m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的顶端C、A与O点在一条直线上,则根据图中数据可得旗杆AB的高为 m.
2.如图,是小明设计用手电来测量某古城墙高度的示意图,点处放一水平的平面镜,光线从点出发经平面镜反射后刚好射到古城墙的顶端处,已知,且测得,那么该古城墙的高度是 .
3.如图①是用杠杆撬石头的示意图,当用力压杠杆时,杠杆绕着支点转动,另一端会向上翘起,石头就被翘动了.在图②中,杠杆的端被向上翘起的距离,动力臂与阻力臂满足(与相交于点),要把这块石头翘起,至少要将杠杆的点向下压 .
4.如图,网高为0.8米,击球点到网的水平距离为3米,小明在打网球时,要使球恰好能打过网,且落点恰好在离网4米的位置上,则球拍击球的高度h为 米.
5.如图所示,一条河流的两岸互相平行,沿南岸有一排大树,每隔4米一棵,沿北岸有一排电线杆,每两根电线杆之间的距离为80米,一同学站在距南岸9米的点P处,正好北岸相邻的两根电线杆被南岸的5棵树遮挡住,那么这条河流的宽度是 米.
6.如图,在四边形ABCD中,AE平分∠BAD交CD于点E,且AB=AE,CBA=∠D+BAD过点E作EG⊥AB,垂足为G.延长BC和AE交于点F,若BF:ED=2:1,EG=2,三角形ABF的面积为7,则AD= .
二、单选题
7.《孙子算经》有首数学歌谣,意思是:有一根竹竿不知道有多长,直立后量出它在太阳下的影子长一丈五尺,同时直立一根一尺五寸的小标杆(如图所示),它的影长五寸(提示:1丈尺,1尺寸),则竹竿的长为( )
A.四丈 B.四丈五尺 C.五丈 D.五丈四尺
8.已知一棵树的影长是30m,同一时刻一根长1.5m的标杆的影长为3m,则这棵树的高度是( ).
A.15m B.60m C.20m D.10 m
9.如图,小强自制了一个小孔成像装置,其中纸筒的长度为,他准备了一支长为的蜡烛,想要得到高度为的像,蜡烛与纸筒的距离为( )
A. B. C. D.
10.图1是《墨经》中记载的“小孔成像”实验图,图2是其示意图,其中物距,像距.若像的高度是m,则物体的高度为( )
A. B. C. D.
11.电筒的灯泡位于点G处,手电筒的光从平面镜上点B处反射后,恰好经过木板的边缘点F,落在墙上的点E处.点E到地面的高度,点F到地面的高度,灯泡到木板的水平距离,墙到木板的水平距离为C.已知光在镜面反射中的入射角等于反射角,图中点A、B、C、D在同一水平面上,则灯泡到地面的高度为( )
A. B. C. D.
12.如图,在平行四边形ABCD中,E为CD上一点,DE:CE=2:3,连结AE,BD,且AE、BD交于点F,则S△DEF:S△ADF:S△BAF等于( )
A.4:10:25 B.4:9:25 C.2:3:5 D.2:5:25
13.如图是小明实验小组成员在小孔成像实验中的影像,蜡烛在刻度尺处,遮光板在刻度尺处,光屏在刻度尺处,量得像高,则蜡烛的长为( )
A. B. C. D.
14.如图,正方形ABCD的边长为4,点P为BC边上的任意一点(不与点B、C重合),且∠DPE=90°,PE交AB于点E,设BP=x,BE=y,则y关于x的函数图象大致是( )
A. B.
C. D.
15.如图,小颖身高为160cm,在阳光下影长AB=240cm,当她走到距离墙角(点D)150cm处时,她的部分影子投射到墙上,则投射在墙上的影子DE的长度为( )
A.50 B.60 C.70 D.80
16.如图,将 沿 边上的中线 平移到 的位置.已知 的面积为16,阴影部分三角形的面积9.若 ,则 等于( )
A.2 B.3 C.4 D.
三、解答题
17.如图,有一块三角形的土地,它的一条边BC=100米,BC边上的高AH=80米.某单位要沿着边BC修一座底面是矩形DEFG的大楼,D、G分别在边AB、AC上.若大楼的宽是40米(即DE=40米),求这个矩形的面积.
18.小聪和他的同学利用影长测量旗杆高度(如图),当1m长的直立竹竿的影长为1.5m时,测量旗杆落在地上的影长为21m,落在墙上的影长为2m.求旗杆的高度.
19.在一次数学活动课上,老师让同学们到操场上测量旗杆的高度,然后回来交流各自的测量方法.小芳的测量方法是:拿一根高3.5米的竹竿直立在离旗杆27米的C处(如图),然后沿BC方向走到D处,这时目测旗杆顶部A与竹竿顶部E恰好在同一直线上,又测得C、D两点的距离为3米,小芳的目高为1.5米,这样便可知道旗杆的高.你认为这种测量方法是否可行?请说明理由.
20.如图,在△ABC中,AB=4cm,BC=8cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P、Q分别从A、B同时出发,经几秒后,点P、B、Q构成的三角形△PBQ与△ABC相似
四、计算题
21.为了测量学校旗杆的高度AB,数学兴趣小组带着标杆和皮尺来到操场进行测量,测 量方案如下:如图,首先,小红在C处放置一平面镜,她从点C沿BC后退,当退行1.8米到D处时,恰好在镜子中看到旗杆顶点A的像,此时测得小红眼睛到地面的距离ED为1.5米;然后,小明在F 处竖立了一根高1.6米的标杆FG,发现地面上的点H、标杆顶点G和旗杆顶点A在一条直线上,此时测得FH为2.4米,DF为3.3米,已知AB⊥BH,ED⊥BH,GF⊥BH,点B、C、D、F、H在一条直线上.
(1)直接写出 ;
(2)请根据以上所测数据,计算学校旗杆AB的高度.
22.学习相似三角形相关知识后,善于思考的小明和小颖两位同学想通过所学计算桥的长.如图,该桥两侧河岸平行,他们在河的对岸选定一个目标作为点,再在河岸的这一边选出点和点,分别在、的延长线上取点、,使得.经测量,米,米,且点到河岸的距离为60米.已知于点,请你根据提供的数据,帮助他们计算桥的长度.
23.课本中有一道作业题:
有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.问加工成的正方形零件的边长是多少mm?
小颖解得此题的答案为48mm,小颖善于反思,她又提出了如下的问题.
(1)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少mm?请你计算.
(2)如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.
答案解析部分
1.【答案】9
【知识点】相似三角形的应用
2.【答案】8
【知识点】相似三角形的应用
3.【答案】
【知识点】相似三角形的应用
4.【答案】1.4
【知识点】相似三角形的应用
5.【答案】36
【知识点】相似三角形的应用
6.【答案】
【知识点】角平分线的性质;相似三角形的判定与性质;相似三角形的应用;角平分线的判定
7.【答案】B
【知识点】相似三角形的应用
8.【答案】A
【知识点】相似三角形的应用
9.【答案】C
【知识点】相似三角形的应用
10.【答案】C
【知识点】相似三角形的应用
11.【答案】A
【知识点】相似三角形的应用
12.【答案】B
【知识点】平行四边形的性质;相似三角形的应用
13.【答案】D
【知识点】相似三角形的判定与性质;相似三角形的应用
14.【答案】A
【知识点】函数的图象;相似三角形的应用
15.【答案】B
【知识点】相似三角形的应用
16.【答案】B
【知识点】相似三角形的应用
17.【答案】解答:由已知得,DG∥BC∴△ADG∽△ABC,∵AH⊥BC∴AH⊥DG于点M,且AM=AH-MH=80-40=40(m) = ,即DG= =50(m),∴S矩形DEFG=DE×DG=2000(m2).
【知识点】相似三角形的应用
18.【答案】解:如图,CD=2m,BD=21m,
∵,
∴DE=1.5CD=3,
∵,
∴AB==16(m).
答:旗杆的高度为16m.
【知识点】相似三角形的应用
19.【答案】这种测量方法可行,旗杆的高为21.5米.
【知识点】相似三角形的判定与性质;相似三角形的应用
20.【答案】解:设经过t秒后,△PBQ与△ABC相似,
∵点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,
∴AP=t,BQ=2t,
∵AB=4,BC=8,
∴BP=AB-AP=4-t,
①当△PBQ∽△ABC时,
∴,
即,
解得:t=2;
②当△PBQ∽△CBA时,
∴,
即,
解得:t=;
综上所述:经过2秒或秒,△PBQ与△ABC相似.
【知识点】相似三角形的性质;相似三角形的应用
21.【答案】(1);(2)学校旗杆AB的高度为25米.
【知识点】相似三角形的应用
22.【答案】桥的长度为90米
【知识点】相似三角形的应用
23.【答案】(1)mm,mm;(2)PN=60mm,mm.
【知识点】相似三角形的应用
21世纪教育网(www.21cnjy.com)
2 / 9
