28.1锐角三角函数(含答案)
图片预览
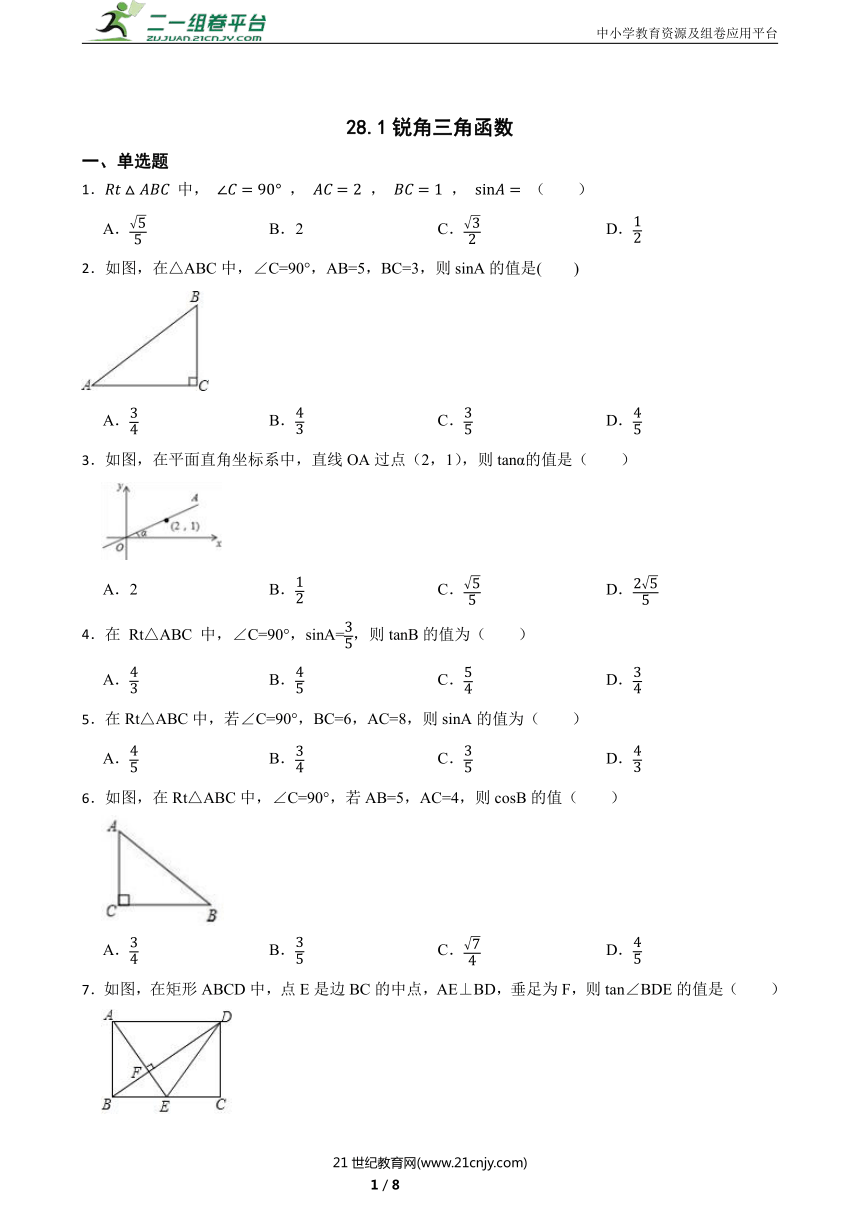


文档简介
中小学教育资源及组卷应用平台
28.1锐角三角函数
一、单选题
1. 中, , , , ( )
A. B.2 C. D.
2.如图,在△ABC中,∠C=90°,AB=5,BC=3,则sinA的值是( )
A. B. C. D.
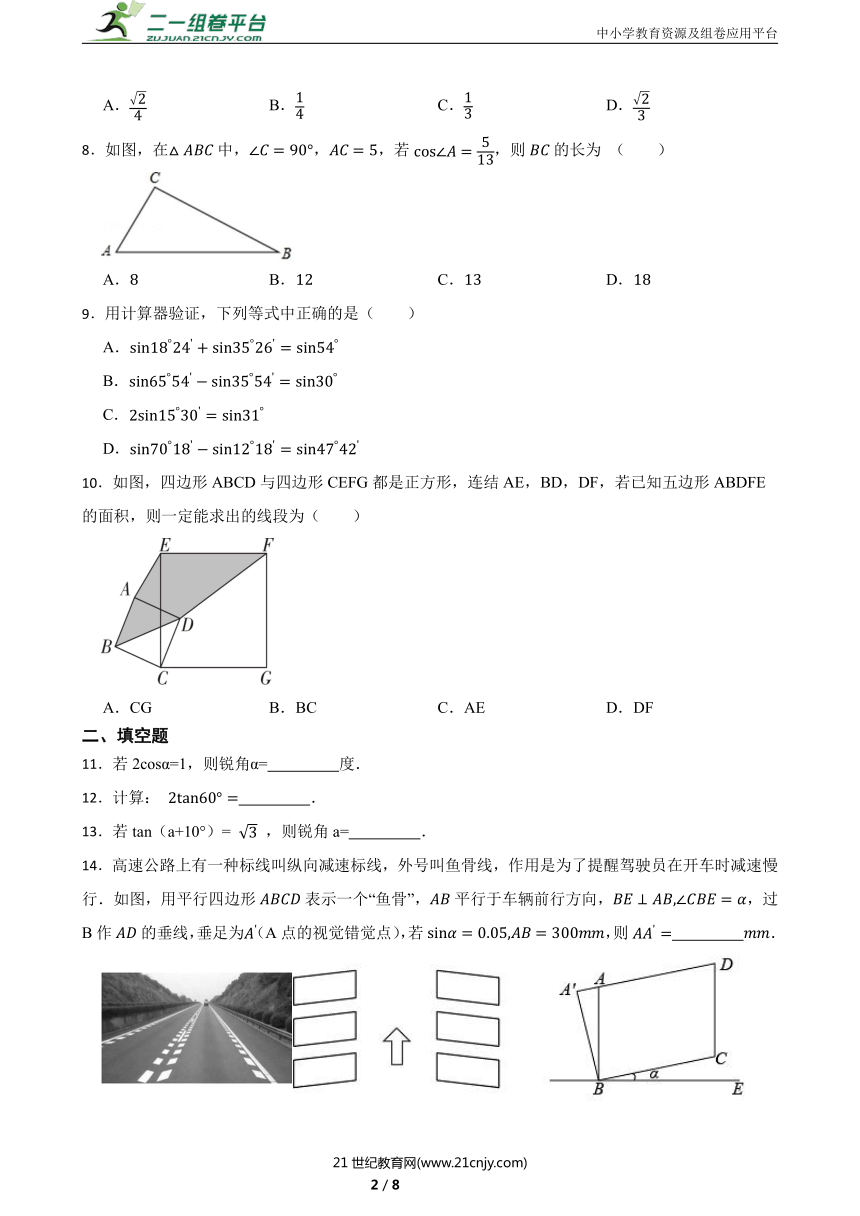
3.如图,在平面直角坐标系中,直线OA过点(2,1),则tanα的值是( )
A.2 B. C. D.
4.在 Rt△ABC 中,∠C=90°,sinA=,则tanB的值为( )
A. B. C. D.
5.在Rt△ABC中,若∠C=90°,BC=6,AC=8,则sinA的值为( )
A. B. C. D.
6.如图,在Rt△ABC中,∠C=90°,若AB=5,AC=4,则cosB的值( )
A. B. C. D.
7.如图,在矩形ABCD中,点E是边BC的中点,AE⊥BD,垂足为F,则tan∠BDE的值是( )
A. B. C. D.
8.如图,在中,,,若,则的长为 ( )
A. B. C. D.
9.用计算器验证,下列等式中正确的是( )
A.
B.
C.
D.
10.如图,四边形ABCD与四边形CEFG都是正方形,连结AE,BD,DF,若已知五边形ABDFE的面积,则一定能求出的线段为( )
A.CG B.BC C.AE D.DF
二、填空题
11.若2cosα=1,则锐角α= 度.
12.计算: .
13.若tan(a+10°)= ,则锐角a= .
14.高速公路上有一种标线叫纵向减速标线,外号叫鱼骨线,作用是为了提醒驾驶员在开车时减速慢行.如图,用平行四边形表示一个“鱼骨”,平行于车辆前行方向,,过B作的垂线,垂足为(A点的视觉错觉点),若,则 .
15.用科学计算器计算:7 ﹣5sin37°= (结果精确到0.1).
16.如图,已知点A是第一象限内横坐标为的一个定点,AC⊥x轴于点M,交直线y=-x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是 .
三、计算题
17.(1)计算:;
(2)化简:
18.计算题:二次根式与分式运算
(1)计算:( )﹣2+( ﹣ )0+(﹣1)1001+( ﹣3 )×tan30°
(2)先化简,再求值: ﹣ ( ﹣a2+b2),其中a=3﹣2 ,b=3 ﹣3.
19.计算题
(1)计算: +cos245°﹣(﹣2)﹣1﹣|﹣ |
(2)先化简,再求值:( ﹣ )÷ ,其中x=2 ,y= .
四、解答题
20.已知 ,且0°<α<45°,求sinα的值.
21.计算: .
22.一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,试求CD的长.
23.如图,在中,是对角线的交点,,垂足分别为点.
(1)求证:.
(2)若,求的值.
答案解析部分
1.【答案】A
【知识点】锐角三角函数的定义
2.【答案】C
【知识点】锐角三角函数的定义
3.【答案】B
【知识点】坐标与图形性质;锐角三角函数的定义
4.【答案】A
【知识点】锐角三角函数的定义
5.【答案】C
【知识点】勾股定理;锐角三角函数的定义
6.【答案】B
【知识点】勾股定理;锐角三角函数的定义
7.【答案】A
【知识点】矩形的性质;相似三角形的判定与性质;锐角三角函数的定义
8.【答案】B
【知识点】锐角三角函数的定义
9.【答案】D
【知识点】计算器—三角函数
10.【答案】A
【知识点】三角形的面积;正方形的性质;锐角三角函数的定义;三角形全等的判定-AAS
11.【答案】60
【知识点】求特殊角的三角函数值
12.【答案】
【知识点】求特殊角的三角函数值
13.【答案】50°
【知识点】求特殊角的三角函数值
14.【答案】15.
【知识点】同角三角函数的关系;互余两角三角函数的关系
15.【答案】42.9
【知识点】计算器在数的开方中的应用;计算器—三角函数;近似数及有效数字
16.【答案】.
【知识点】相似三角形的判定与性质;锐角三角函数的定义
17.【答案】(1);(2)
【知识点】完全平方公式及运用;求特殊角的三角函数值
18.【答案】(1)解:原式=9+1﹣1+(2 ﹣3 )×
=9﹣ ×
=9﹣3
=6
(2)解:当a=3﹣2 ,b=3 ﹣3时,
原式= ﹣ [ ﹣(a2﹣b2)]
= ﹣ [ ﹣(a﹣b)(a+b)]
= ﹣ +a+b
=a+b
=3﹣2 +3 ﹣3
=
【知识点】实数的运算;分式的化简求值;零指数幂;负整数指数幂;求特殊角的三角函数值
19.【答案】(1)解: +cos245°﹣(﹣2)﹣1﹣|﹣ |
=0.2+
=0.2+
=0.7;
(2)解:( ﹣ )÷
=
=
=
=
= ,
当x=2 ,y= 时,原式= .
【知识点】实数的运算;分式的化简求值;负整数指数幂;求特殊角的三角函数值
20.【答案】解:∵ ,
∴(sinα+cosα)2= ,即sin2α+cos2α+2sinα cosα= ,
而sin2α+cos2α=1,
∴2sinα cosα= ,
∴1﹣2sinα cosα= ,即sin2α+cos2α﹣2sinα cosα= ,
∴(sinα﹣cosα)2= ,
∵0°<α<45°,
∴sinα<cosα,
∴sinα﹣cosα=﹣ ,
而 ,
∴2sinα= ,
∴sinα= .
【知识点】互余两角三角函数的关系
21.【答案】解: ,
= ,
= .
【知识点】零指数幂;二次根式的混合运算;求特殊角的三角函数值
22.【答案】解:过点B作BM⊥FD于点M,在△ACB中,∠ACB=90°,∠A=60°,AC=10,∴∠ABC=30°,BC=AC×tan60°=10 ,∵AB∥CF,∴BM=BC×sin30°=10 × =5 ,CM=BC×cos30°=15,在△EFD中,∠F=90°,∠E=45°,∴∠EDF=45°,∴MD=BM=5 ,∴CD=CM﹣MD=15﹣5 .
【知识点】平行线的性质;等腰三角形的性质;锐角三角函数的定义
23.【答案】(1)证明:证明:∵四边形ABCD是平行四边形,
∴OB=OD,OA=OC,
∵BE⊥AC,DF⊥AC,
∴∠OEB=∠OFD=90°,
在△OEB和△OFD中,,
∴△OEB≌△OFD(AAS),
∴OE=OF,
∴OA﹣OF=OC﹣OE,
∴AF=CE;
(2)解:由(1)得:OE=OF,
∴OE=OF=6,
∵OD=DB,DB=20,
∴OD=10,
∵BF⊥AC,
∴∠OFD=90°,
,
∴.
【知识点】三角形全等及其性质;三角形全等的判定;平行四边形的性质;锐角三角函数的定义
21世纪教育网(www.21cnjy.com)
2 / 8
28.1锐角三角函数
一、单选题
1. 中, , , , ( )
A. B.2 C. D.
2.如图,在△ABC中,∠C=90°,AB=5,BC=3,则sinA的值是( )
A. B. C. D.
3.如图,在平面直角坐标系中,直线OA过点(2,1),则tanα的值是( )
A.2 B. C. D.
4.在 Rt△ABC 中,∠C=90°,sinA=,则tanB的值为( )
A. B. C. D.
5.在Rt△ABC中,若∠C=90°,BC=6,AC=8,则sinA的值为( )
A. B. C. D.
6.如图,在Rt△ABC中,∠C=90°,若AB=5,AC=4,则cosB的值( )
A. B. C. D.
7.如图,在矩形ABCD中,点E是边BC的中点,AE⊥BD,垂足为F,则tan∠BDE的值是( )
A. B. C. D.
8.如图,在中,,,若,则的长为 ( )
A. B. C. D.
9.用计算器验证,下列等式中正确的是( )
A.
B.
C.
D.
10.如图,四边形ABCD与四边形CEFG都是正方形,连结AE,BD,DF,若已知五边形ABDFE的面积,则一定能求出的线段为( )
A.CG B.BC C.AE D.DF
二、填空题
11.若2cosα=1,则锐角α= 度.
12.计算: .
13.若tan(a+10°)= ,则锐角a= .
14.高速公路上有一种标线叫纵向减速标线,外号叫鱼骨线,作用是为了提醒驾驶员在开车时减速慢行.如图,用平行四边形表示一个“鱼骨”,平行于车辆前行方向,,过B作的垂线,垂足为(A点的视觉错觉点),若,则 .
15.用科学计算器计算:7 ﹣5sin37°= (结果精确到0.1).
16.如图,已知点A是第一象限内横坐标为的一个定点,AC⊥x轴于点M,交直线y=-x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是 .
三、计算题
17.(1)计算:;
(2)化简:
18.计算题:二次根式与分式运算
(1)计算:( )﹣2+( ﹣ )0+(﹣1)1001+( ﹣3 )×tan30°
(2)先化简,再求值: ﹣ ( ﹣a2+b2),其中a=3﹣2 ,b=3 ﹣3.
19.计算题
(1)计算: +cos245°﹣(﹣2)﹣1﹣|﹣ |
(2)先化简,再求值:( ﹣ )÷ ,其中x=2 ,y= .
四、解答题
20.已知 ,且0°<α<45°,求sinα的值.
21.计算: .
22.一副直角三角板如图放置,点C在FD的延长线上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,试求CD的长.
23.如图,在中,是对角线的交点,,垂足分别为点.
(1)求证:.
(2)若,求的值.
答案解析部分
1.【答案】A
【知识点】锐角三角函数的定义
2.【答案】C
【知识点】锐角三角函数的定义
3.【答案】B
【知识点】坐标与图形性质;锐角三角函数的定义
4.【答案】A
【知识点】锐角三角函数的定义
5.【答案】C
【知识点】勾股定理;锐角三角函数的定义
6.【答案】B
【知识点】勾股定理;锐角三角函数的定义
7.【答案】A
【知识点】矩形的性质;相似三角形的判定与性质;锐角三角函数的定义
8.【答案】B
【知识点】锐角三角函数的定义
9.【答案】D
【知识点】计算器—三角函数
10.【答案】A
【知识点】三角形的面积;正方形的性质;锐角三角函数的定义;三角形全等的判定-AAS
11.【答案】60
【知识点】求特殊角的三角函数值
12.【答案】
【知识点】求特殊角的三角函数值
13.【答案】50°
【知识点】求特殊角的三角函数值
14.【答案】15.
【知识点】同角三角函数的关系;互余两角三角函数的关系
15.【答案】42.9
【知识点】计算器在数的开方中的应用;计算器—三角函数;近似数及有效数字
16.【答案】.
【知识点】相似三角形的判定与性质;锐角三角函数的定义
17.【答案】(1);(2)
【知识点】完全平方公式及运用;求特殊角的三角函数值
18.【答案】(1)解:原式=9+1﹣1+(2 ﹣3 )×
=9﹣ ×
=9﹣3
=6
(2)解:当a=3﹣2 ,b=3 ﹣3时,
原式= ﹣ [ ﹣(a2﹣b2)]
= ﹣ [ ﹣(a﹣b)(a+b)]
= ﹣ +a+b
=a+b
=3﹣2 +3 ﹣3
=
【知识点】实数的运算;分式的化简求值;零指数幂;负整数指数幂;求特殊角的三角函数值
19.【答案】(1)解: +cos245°﹣(﹣2)﹣1﹣|﹣ |
=0.2+
=0.2+
=0.7;
(2)解:( ﹣ )÷
=
=
=
=
= ,
当x=2 ,y= 时,原式= .
【知识点】实数的运算;分式的化简求值;负整数指数幂;求特殊角的三角函数值
20.【答案】解:∵ ,
∴(sinα+cosα)2= ,即sin2α+cos2α+2sinα cosα= ,
而sin2α+cos2α=1,
∴2sinα cosα= ,
∴1﹣2sinα cosα= ,即sin2α+cos2α﹣2sinα cosα= ,
∴(sinα﹣cosα)2= ,
∵0°<α<45°,
∴sinα<cosα,
∴sinα﹣cosα=﹣ ,
而 ,
∴2sinα= ,
∴sinα= .
【知识点】互余两角三角函数的关系
21.【答案】解: ,
= ,
= .
【知识点】零指数幂;二次根式的混合运算;求特殊角的三角函数值
22.【答案】解:过点B作BM⊥FD于点M,在△ACB中,∠ACB=90°,∠A=60°,AC=10,∴∠ABC=30°,BC=AC×tan60°=10 ,∵AB∥CF,∴BM=BC×sin30°=10 × =5 ,CM=BC×cos30°=15,在△EFD中,∠F=90°,∠E=45°,∴∠EDF=45°,∴MD=BM=5 ,∴CD=CM﹣MD=15﹣5 .
【知识点】平行线的性质;等腰三角形的性质;锐角三角函数的定义
23.【答案】(1)证明:证明:∵四边形ABCD是平行四边形,
∴OB=OD,OA=OC,
∵BE⊥AC,DF⊥AC,
∴∠OEB=∠OFD=90°,
在△OEB和△OFD中,,
∴△OEB≌△OFD(AAS),
∴OE=OF,
∴OA﹣OF=OC﹣OE,
∴AF=CE;
(2)解:由(1)得:OE=OF,
∴OE=OF=6,
∵OD=DB,DB=20,
∴OD=10,
∵BF⊥AC,
∴∠OFD=90°,
,
∴.
【知识点】三角形全等及其性质;三角形全等的判定;平行四边形的性质;锐角三角函数的定义
21世纪教育网(www.21cnjy.com)
2 / 8
