28.2解直角三角形及其应用(含答案)
文档属性
| 名称 | 28.2解直角三角形及其应用(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 711.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-27 14:10:57 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
28,2解直角三角形及其应用
一、单选题
1.在中,,,,则的值是( )
A.4 B.5 C.8 D.10
2.如图,一学生要测量校园内一棵水杉树的高度,他站在距离水杉树的处,测得树顶的仰角为,已知测角仪的架高,那么这棵水杉树高是( )
A. B. C. D.
3.如图,正方形内接于,等边的顶点,分别在,上,交,于点,,则的值等于( )
A. B. C. D.2
4.如图,一艘轮船从位于灯塔C的北偏东60°方向,距离灯塔60 n mile的小岛A出发,沿正南方向航行一段时间后,到达位于灯塔C的南偏东45°方向上的B处,这时轮船B与小岛A的距离是( )
A. n mile B.60 n mile
C.120 n mile D.n mile
5.如图所示,热气球探测器在A点处,点B为楼顶,点C为楼底,AD为水平线,EF为经过点A的铅垂线,则下列说法正确的有( )
①∠1为仰角; ②∠2为仰角; ③∠3为俯角; ④∠4为俯角.
A.1个 B.2个 C.3个 D.4个
6.“折竹抵地”问题源自《九章算术》中,即:今有竹高一丈,末折抵地,去本四尺,问折者高几何?意思是:一根竹子,原高一丈,一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部4尺远(如图),则折断后的竹子高度为多少尺?(1丈=10尺)( )
A.3 B.5 C. D.4
7.在Rt△ABC中,∠C=90°,AB=2BC,则sinB的值为( ).
A. B. C. D.1
8.一人乘雪橇沿坡比1: 的斜坡笔直滑下,滑下的距离s(m)与时间t(s)之间的关系为s=8t+2t2,若滑到坡底的时间为4s,则此人下降的高度为( )
A.16 m B.32m C.32 m D.64m
9.如图, P是∠α的边OA上一点,且点P的坐标为(3,4),则sinα=( )
A. B. C. D.
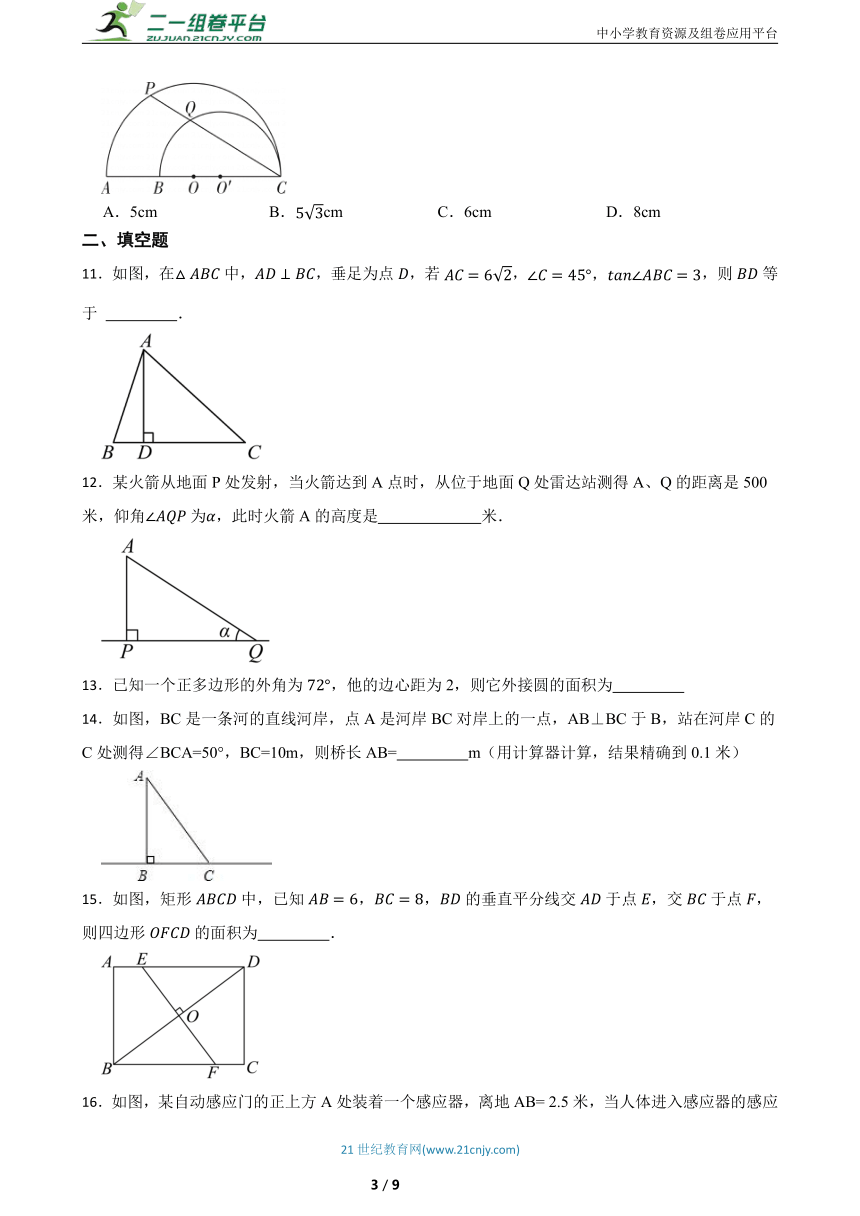
10.如图,AC,BC是两个半圆的直径,∠ACP=30°,AB=10 cm,则PQ的长为( ).
A.5cm B.cm C.6cm D.8cm
二、填空题
11.如图,在中,,垂足为点,若,,则等于 .
12.某火箭从地面P处发射,当火箭达到A点时,从位于地面Q处雷达站测得A、Q的距离是500米,仰角为,此时火箭A的高度是 米.
13.已知一个正多边形的外角为,他的边心距为2,则它外接圆的面积为
14.如图,BC是一条河的直线河岸,点A是河岸BC对岸上的一点,AB⊥BC于B,站在河岸C的C处测得∠BCA=50°,BC=10m,则桥长AB= m(用计算器计算,结果精确到0.1米)
15.如图,矩形中,已知,,的垂直平分线交于点,交于点,则四边形的面积为 .
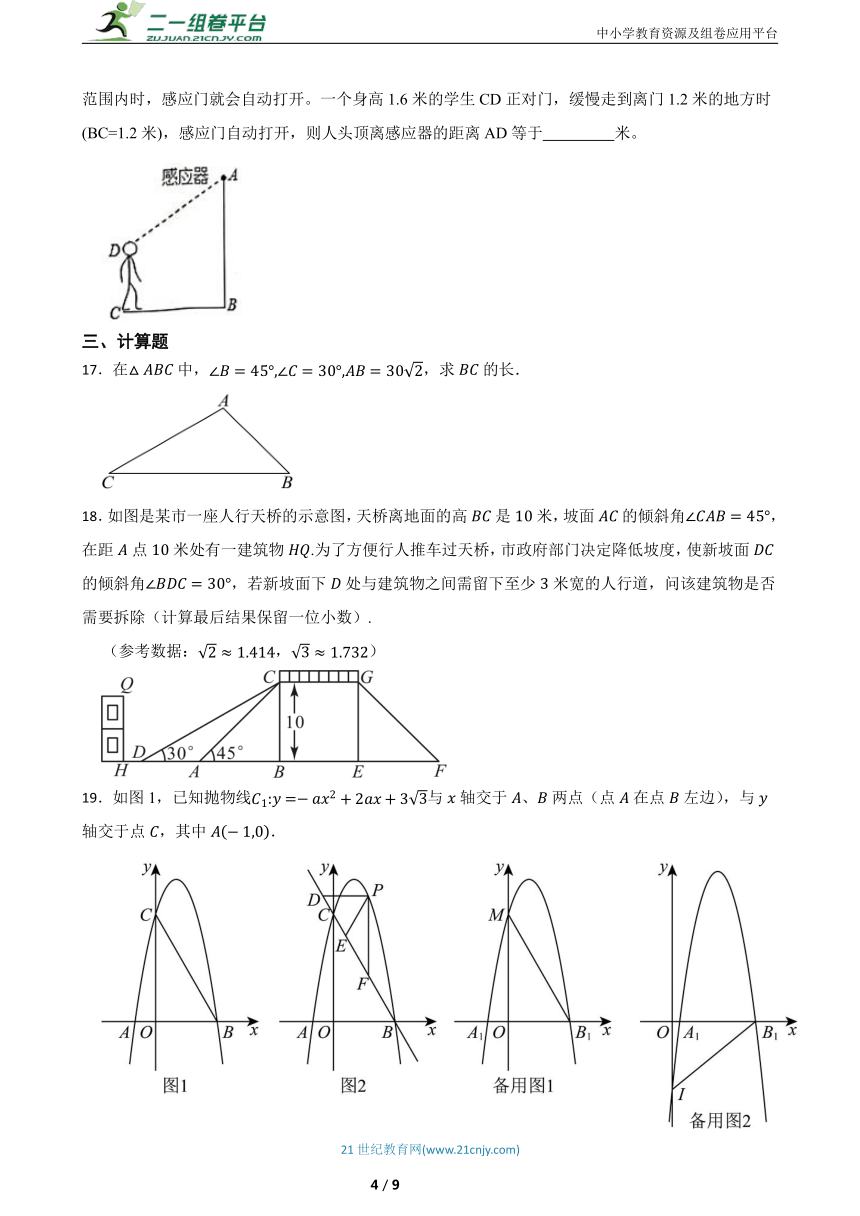
16.如图,某自动感应门的正上方A处装着一个感应器,离地AB= 2.5米,当人体进入感应器的感应范围内时,感应门就会自动打开。一个身高1.6米的学生CD正对门,缓慢走到离门1.2米的地方时(BC=1.2米),感应门自动打开,则人头顶离感应器的距离AD等于 米。
三、计算题
17.在中,,求的长.
18.如图是某市一座人行天桥的示意图,天桥离地面的高是米,坡面的倾斜角,在距点米处有一建筑物.为了方便行人推车过天桥,市政府部门决定降低坡度,使新坡面的倾斜角,若新坡面下处与建筑物之间需留下至少米宽的人行道,问该建筑物是否需要拆除(计算最后结果保留一位小数).
(参考数据:,)
19.如图1,已知抛物线与轴交于、两点(点在点左边),与轴交于点,其中.
(1)求线段的长度.
(2)如图,点是直线上方抛物线上的一动点,过点作轴交于点,作轴交于点,为中点,连接,请求出的最大值以及此时点的坐标.
(3)将抛物线水平向右平移个单位后得到抛物线,点、点的对应点分别为点、点,抛物线与轴交于点(点不与原点重合),连接、.在平移过程中,当时,请直接写出的值.
四、解答题
20.如图,为了测量山坡的护坡石坝坝顶C与坝脚B之间的距离,把一根长为6米的竹竿斜靠在石坝旁,量出竿长1米处距离地面的高度为0.6米,又测得石坝与地面的倾斜角为.求石坝坝顶C与坝脚B之间的距离.(结果精确到,参考数据:,,)
21.如图,某无人机兴趣小组在操场上开展活动,此时无人机在离地面30米的D处,无人机测得操控者A的俯角为30°,测得教学楼BC顶端点C处的俯角为45°.又经过人工测量测得操控者A和教学楼BC之间的距离为57米.求教学楼BC的高度.(点A,B,C,D都在同一平面上,结果保留根号)
22.如图1,有个酒精喷壶放置在水平地面上, 与地面平行,点B是喷嘴,点C是压柄的端点,且 ;在其示意图2中, , , ,求喷嘴 与压柄端点C的距离(结果精确到 ).(参考数据: , )
23.如图1,在的平分线上一点任取一点M,恰好是和的比例中项,则称四边形为“和谐四边形”.
(1)在图1中,若,四边形为“和谐四边形”,则________;
(2)如图2,(其中为锐角),,连接,若四边形为“和谐四边形”,用含的式子分别表示的度数和的面积;
(3)如图3,坐标平面内有一点,满足,过点C作直线分别与x轴和y轴交于A、B两点,且.试分析:在平面直角坐标系内是否存在一点M,使得四边形恰好为“和谐四边形”.若存在,直接写出点M坐标.
答案解析部分
1.【答案】D
【知识点】解直角三角形
2.【答案】A
【知识点】矩形的判定与性质;解直角三角形的实际应用﹣仰角俯角问题
3.【答案】C
【知识点】圆内接正多边形;解直角三角形
4.【答案】D
【知识点】解直角三角形的实际应用﹣方向角问题
5.【答案】B
【知识点】解直角三角形的实际应用﹣仰角俯角问题
6.【答案】C
【知识点】勾股定理;解直角三角形的其他实际应用
7.【答案】C
【知识点】锐角三角函数的定义;解直角三角形
8.【答案】B
【知识点】解直角三角形的实际应用﹣坡度坡角问题
9.【答案】D
【知识点】解直角三角形
10.【答案】B
【知识点】含30°角的直角三角形;圆周角定理;求特殊角的三角函数值;解直角三角形
11.【答案】
【知识点】解直角三角形
12.【答案】
【知识点】解直角三角形的实际应用﹣仰角俯角问题
13.【答案】
【知识点】多边形内角与外角;圆内接正多边形;解直角三角形
14.【答案】11.9
【知识点】解直角三角形的其他实际应用
15.【答案】
【知识点】勾股定理;矩形的性质;解直角三角形
16.【答案】1.5
【知识点】勾股定理;解直角三角形的其他实际应用
17.【答案】
【知识点】勾股定理;解直角三角形
18.【答案】该建筑物需要拆除.
【知识点】解直角三角形的实际应用﹣坡度坡角问题
19.【答案】(1);
(2);;
(3),.
【知识点】解直角三角形
20.【答案】石坝坝顶C与坝脚B之间的距离为米.
【知识点】解直角三角形的其他实际应用
21.【答案】教学楼BC的高度为米
【知识点】解直角三角形的实际应用﹣仰角俯角问题
22.【答案】解:设 ,
∵ , ,
∴ , ,
,
,
.
故喷嘴 与压柄端点C的距离为 .
【知识点】解直角三角形的其他实际应用
23.【答案】(1)
(2),
(3)或
【知识点】坐标与图形性质;比例线段;相似三角形的判定与性质;解直角三角形
21世纪教育网(www.21cnjy.com)
5 / 9
28,2解直角三角形及其应用
一、单选题
1.在中,,,,则的值是( )
A.4 B.5 C.8 D.10
2.如图,一学生要测量校园内一棵水杉树的高度,他站在距离水杉树的处,测得树顶的仰角为,已知测角仪的架高,那么这棵水杉树高是( )
A. B. C. D.
3.如图,正方形内接于,等边的顶点,分别在,上,交,于点,,则的值等于( )
A. B. C. D.2
4.如图,一艘轮船从位于灯塔C的北偏东60°方向,距离灯塔60 n mile的小岛A出发,沿正南方向航行一段时间后,到达位于灯塔C的南偏东45°方向上的B处,这时轮船B与小岛A的距离是( )
A. n mile B.60 n mile
C.120 n mile D.n mile
5.如图所示,热气球探测器在A点处,点B为楼顶,点C为楼底,AD为水平线,EF为经过点A的铅垂线,则下列说法正确的有( )
①∠1为仰角; ②∠2为仰角; ③∠3为俯角; ④∠4为俯角.
A.1个 B.2个 C.3个 D.4个
6.“折竹抵地”问题源自《九章算术》中,即:今有竹高一丈,末折抵地,去本四尺,问折者高几何?意思是:一根竹子,原高一丈,一阵风将竹子折断,其竹梢恰好抵地,抵地处离竹子底部4尺远(如图),则折断后的竹子高度为多少尺?(1丈=10尺)( )
A.3 B.5 C. D.4
7.在Rt△ABC中,∠C=90°,AB=2BC,则sinB的值为( ).
A. B. C. D.1
8.一人乘雪橇沿坡比1: 的斜坡笔直滑下,滑下的距离s(m)与时间t(s)之间的关系为s=8t+2t2,若滑到坡底的时间为4s,则此人下降的高度为( )
A.16 m B.32m C.32 m D.64m
9.如图, P是∠α的边OA上一点,且点P的坐标为(3,4),则sinα=( )
A. B. C. D.
10.如图,AC,BC是两个半圆的直径,∠ACP=30°,AB=10 cm,则PQ的长为( ).
A.5cm B.cm C.6cm D.8cm
二、填空题
11.如图,在中,,垂足为点,若,,则等于 .
12.某火箭从地面P处发射,当火箭达到A点时,从位于地面Q处雷达站测得A、Q的距离是500米,仰角为,此时火箭A的高度是 米.
13.已知一个正多边形的外角为,他的边心距为2,则它外接圆的面积为
14.如图,BC是一条河的直线河岸,点A是河岸BC对岸上的一点,AB⊥BC于B,站在河岸C的C处测得∠BCA=50°,BC=10m,则桥长AB= m(用计算器计算,结果精确到0.1米)
15.如图,矩形中,已知,,的垂直平分线交于点,交于点,则四边形的面积为 .
16.如图,某自动感应门的正上方A处装着一个感应器,离地AB= 2.5米,当人体进入感应器的感应范围内时,感应门就会自动打开。一个身高1.6米的学生CD正对门,缓慢走到离门1.2米的地方时(BC=1.2米),感应门自动打开,则人头顶离感应器的距离AD等于 米。
三、计算题
17.在中,,求的长.
18.如图是某市一座人行天桥的示意图,天桥离地面的高是米,坡面的倾斜角,在距点米处有一建筑物.为了方便行人推车过天桥,市政府部门决定降低坡度,使新坡面的倾斜角,若新坡面下处与建筑物之间需留下至少米宽的人行道,问该建筑物是否需要拆除(计算最后结果保留一位小数).
(参考数据:,)
19.如图1,已知抛物线与轴交于、两点(点在点左边),与轴交于点,其中.
(1)求线段的长度.
(2)如图,点是直线上方抛物线上的一动点,过点作轴交于点,作轴交于点,为中点,连接,请求出的最大值以及此时点的坐标.
(3)将抛物线水平向右平移个单位后得到抛物线,点、点的对应点分别为点、点,抛物线与轴交于点(点不与原点重合),连接、.在平移过程中,当时,请直接写出的值.
四、解答题
20.如图,为了测量山坡的护坡石坝坝顶C与坝脚B之间的距离,把一根长为6米的竹竿斜靠在石坝旁,量出竿长1米处距离地面的高度为0.6米,又测得石坝与地面的倾斜角为.求石坝坝顶C与坝脚B之间的距离.(结果精确到,参考数据:,,)
21.如图,某无人机兴趣小组在操场上开展活动,此时无人机在离地面30米的D处,无人机测得操控者A的俯角为30°,测得教学楼BC顶端点C处的俯角为45°.又经过人工测量测得操控者A和教学楼BC之间的距离为57米.求教学楼BC的高度.(点A,B,C,D都在同一平面上,结果保留根号)
22.如图1,有个酒精喷壶放置在水平地面上, 与地面平行,点B是喷嘴,点C是压柄的端点,且 ;在其示意图2中, , , ,求喷嘴 与压柄端点C的距离(结果精确到 ).(参考数据: , )
23.如图1,在的平分线上一点任取一点M,恰好是和的比例中项,则称四边形为“和谐四边形”.
(1)在图1中,若,四边形为“和谐四边形”,则________;
(2)如图2,(其中为锐角),,连接,若四边形为“和谐四边形”,用含的式子分别表示的度数和的面积;
(3)如图3,坐标平面内有一点,满足,过点C作直线分别与x轴和y轴交于A、B两点,且.试分析:在平面直角坐标系内是否存在一点M,使得四边形恰好为“和谐四边形”.若存在,直接写出点M坐标.
答案解析部分
1.【答案】D
【知识点】解直角三角形
2.【答案】A
【知识点】矩形的判定与性质;解直角三角形的实际应用﹣仰角俯角问题
3.【答案】C
【知识点】圆内接正多边形;解直角三角形
4.【答案】D
【知识点】解直角三角形的实际应用﹣方向角问题
5.【答案】B
【知识点】解直角三角形的实际应用﹣仰角俯角问题
6.【答案】C
【知识点】勾股定理;解直角三角形的其他实际应用
7.【答案】C
【知识点】锐角三角函数的定义;解直角三角形
8.【答案】B
【知识点】解直角三角形的实际应用﹣坡度坡角问题
9.【答案】D
【知识点】解直角三角形
10.【答案】B
【知识点】含30°角的直角三角形;圆周角定理;求特殊角的三角函数值;解直角三角形
11.【答案】
【知识点】解直角三角形
12.【答案】
【知识点】解直角三角形的实际应用﹣仰角俯角问题
13.【答案】
【知识点】多边形内角与外角;圆内接正多边形;解直角三角形
14.【答案】11.9
【知识点】解直角三角形的其他实际应用
15.【答案】
【知识点】勾股定理;矩形的性质;解直角三角形
16.【答案】1.5
【知识点】勾股定理;解直角三角形的其他实际应用
17.【答案】
【知识点】勾股定理;解直角三角形
18.【答案】该建筑物需要拆除.
【知识点】解直角三角形的实际应用﹣坡度坡角问题
19.【答案】(1);
(2);;
(3),.
【知识点】解直角三角形
20.【答案】石坝坝顶C与坝脚B之间的距离为米.
【知识点】解直角三角形的其他实际应用
21.【答案】教学楼BC的高度为米
【知识点】解直角三角形的实际应用﹣仰角俯角问题
22.【答案】解:设 ,
∵ , ,
∴ , ,
,
,
.
故喷嘴 与压柄端点C的距离为 .
【知识点】解直角三角形的其他实际应用
23.【答案】(1)
(2),
(3)或
【知识点】坐标与图形性质;比例线段;相似三角形的判定与性质;解直角三角形
21世纪教育网(www.21cnjy.com)
5 / 9
