第28章锐角三角函数综合检测题(含答案)
文档属性
| 名称 | 第28章锐角三角函数综合检测题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 846.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-27 14:16:27 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第28章锐角三角函数综合检测题
一、填空题
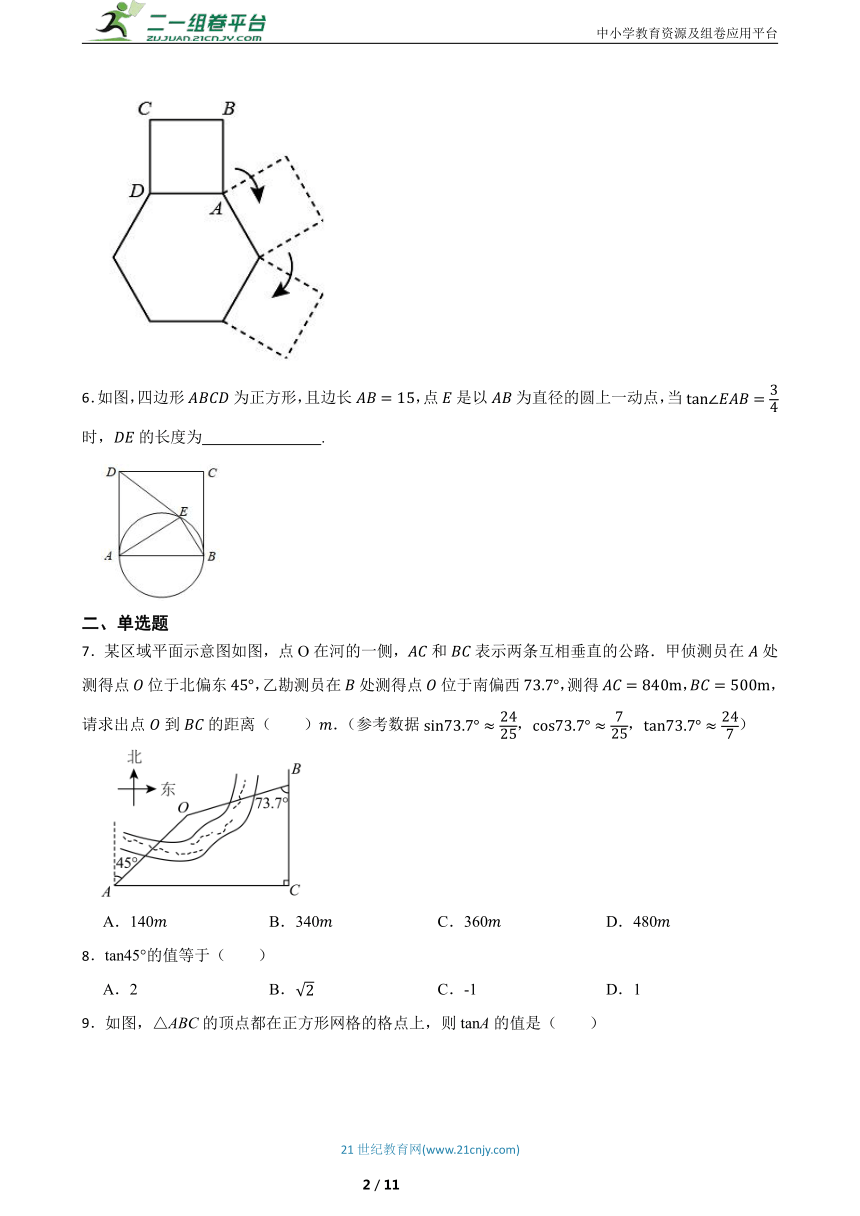
1.某数学兴趣小组测量校园内一棵树的高度,采用以下方法:如图,把支架放在离树适当距离的水平地面上的点F处,再把镜子水平放在支架上的点E处,然后沿着直线后退至点D处,这时恰好在镜子里看到树的顶端A,再用皮尺分别测量,,观测者目高的长,利用测得的数据可以求出这棵树的高度.已知于点D,于点F,于点B,米,米,米,米,则这棵树的高度(的长)是 米.
2.在中,已知,是锐角,若,则的度数为 .
3.如图所示,拧开一个边长为的正六角形螺帽时,扳手张开的开口,则边长 .
4.已知 ,则 = .
5.如图,边长为3的正方形ABCD在正六边形外部做顺时针方向的滚动运动,滚动一周回到初始位置时停止,点A在滚动过程中到出发点的最大距离是 .
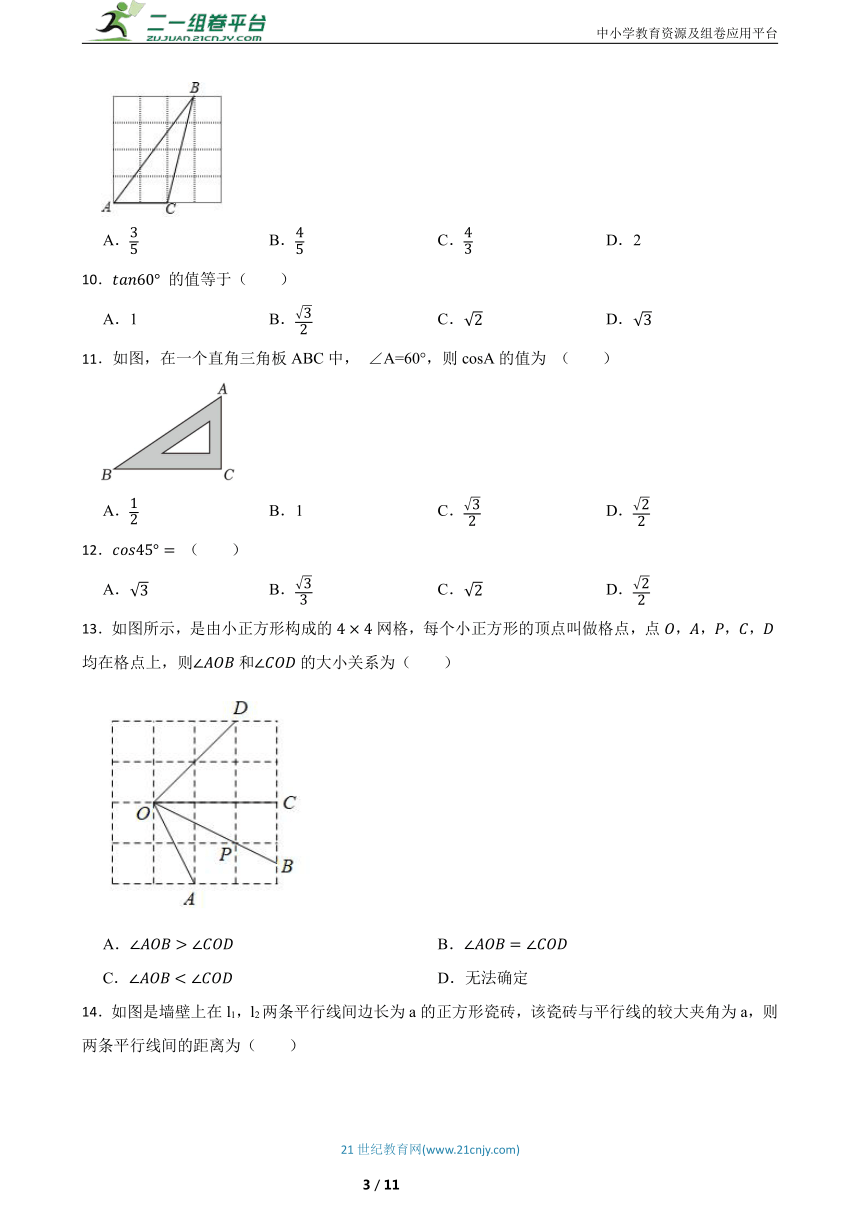
6.如图,四边形为正方形,且边长,点是以为直径的圆上一动点,当时,的长度为 .
二、单选题
7.某区域平面示意图如图,点O在河的一侧,和表示两条互相垂直的公路.甲侦测员在处测得点位于北偏东,乙勘测员在处测得点位于南偏西,测得,,请求出点到的距离( ).(参考数据,,)
A.140 B.340 C.360 D.480
8.tan45°的值等于( )
A.2 B. C.-1 D.1
9.如图,△ABC的顶点都在正方形网格的格点上,则tanA的值是( )
A. B. C. D.2
10. 的值等于( )
A.1 B. C. D.
11.如图,在一个直角三角板ABC中, ∠A=60°,则cosA的值为 ( )
A. B.1 C. D.
12. ( )
A. B. C. D.
13.如图所示,是由小正方形构成的网格,每个小正方形的顶点叫做格点,点,,,,均在格点上,则和的大小关系为( )
A. B.
C. D.无法确定
14.如图是墙壁上在l1,l2两条平行线间边长为a的正方形瓷砖,该瓷砖与平行线的较大夹角为a,则两条平行线间的距离为( )
A.asinα B.asinα+acosα
C.2acosα D.asinα﹣acosα
15.如图,,点在上,且,是上的点,在上找点,以为边,, ,为顶点作正方形,则的长不可能是( )
A. B. C. D.
16.如图,抛物线y=-x2+k与x轴交于A(-3,0)和B(3,0),有一动点C在线段AB上从点A运动到点B(不与A,B重合),分别以AC,BC为底边作等腰△ADC和等腰△BEC,点D,E恰好落在此抛物线上,在整个运动过程中, ∠DCE的变化情况是( )
A.保持不变 B.一直减小
C.先增大后减小 D.先减小后增大
三、解答题
17.某电脑桌生产厂家生产了一种平板电脑桌,其实物图如图1所示,此电脑桌的桌面可调节,图2和图3是其调节桌面的侧面示意图,在点C处安装一根长度一定的支撑杆CB,且AC=BC=20cm,点B可在AD上滑动,当B滑动到D处,电脑的承载面AE与AD重合.
(1)如图2,当BC⊥AC时,求电脑的承载面最高点E与B之间的距离;
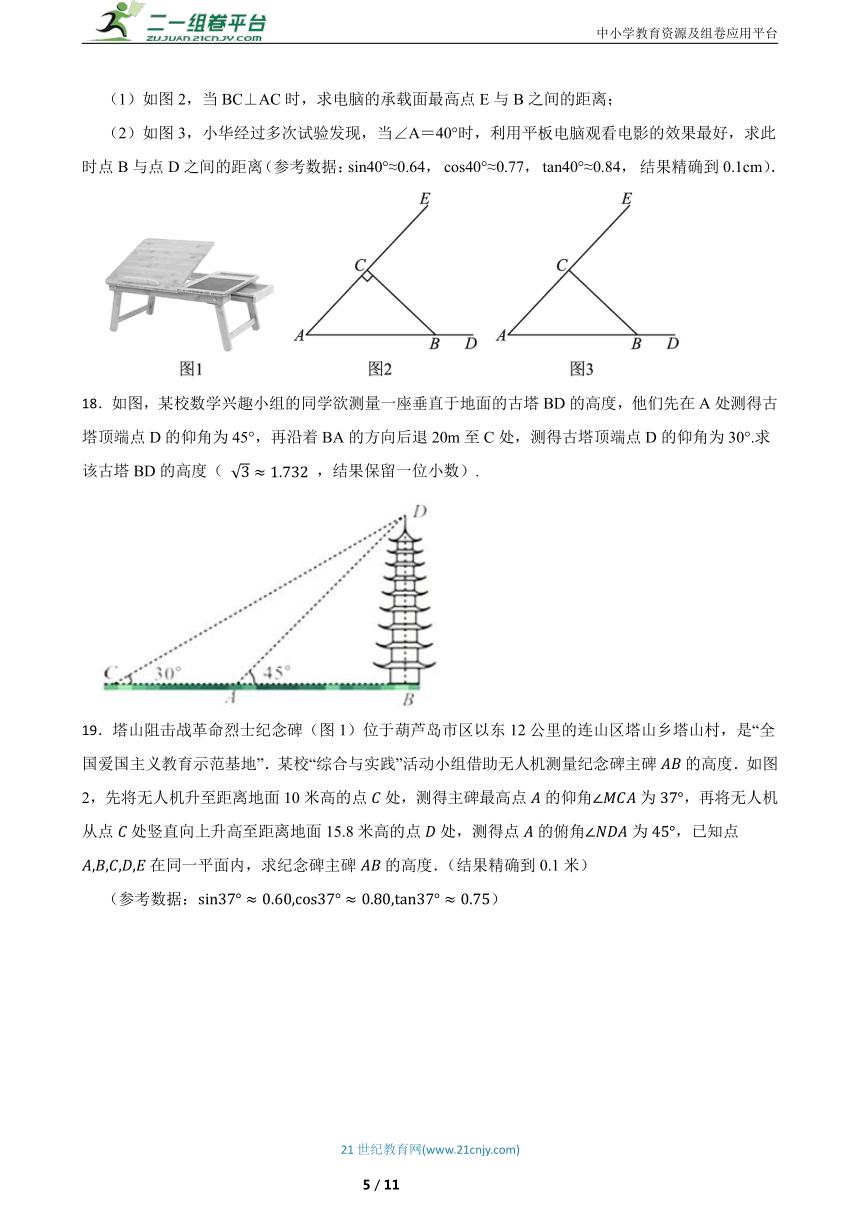
(2)如图3,小华经过多次试验发现,当∠A=40°时,利用平板电脑观看电影的效果最好,求此时点B与点D之间的距离(参考数据:sin40°≈0.64, cos40°≈0.77, tan40°≈0.84, 结果精确到0.1cm).
18.如图,某校数学兴趣小组的同学欲测量一座垂直于地面的古塔BD的高度,他们先在A处测得古塔顶端点D的仰角为45°,再沿着BA的方向后退20m至C处,测得古塔顶端点D的仰角为30°.求该古塔BD的高度( ,结果保留一位小数).
19.塔山阻击战革命烈士纪念碑(图1)位于葫芦岛市区以东12公里的连山区塔山乡塔山村,是“全国爱国主义教育示范基地”.某校“综合与实践”活动小组借助无人机测量纪念碑主碑的高度.如图2,先将无人机升至距离地面10米高的点处,测得主碑最高点的仰角为,再将无人机从点处竖直向上升高至距离地面15.8米高的点处,测得点的俯角为,已知点在同一平面内,求纪念碑主碑的高度.(结果精确到0.1米)
(参考数据:)
20.在一次课外活动中,某数学兴趣小组测量一棵树 的高度.如图所示,测得斜坡 的坡度 ,坡底 的长为8米,在 处测得树 顶部 的仰角为 ,在 处测得树 顶部 的仰角为 ,求树高 .(结果保留根号)
21.2023年5月30日,神舟十六号载人飞船发射取得圆满成功,3名航天员顺利进驻中国空间站,如图中的照片展示了中国空间站上机械臂的一种工作状态,当两臂,两臂夹角时,求A,B两点间的距离.(结果精确到,参考数据,,)
22.如图,直线与轴交于点,与反比例函数,过作轴于点,且.
(1)求反比例函数表达式;
(2)点是反比例函数图象上的点,在轴上是否存在点,使得最小?若存在,求出点的坐标;若不存在,请说明理由;
(3)将直线向下平移个单位后与反比例函数的图象交于一点,求的值.
四、计算题
23.计算:.
24.如图,在一个18米高的楼顶上有一信号塔DC,李明同学为了测量信号塔的高度,在地面的A处测的信号塔下端D的仰角为30°,然后他正对塔的方向前进了18米到达地面的B处,又测得信号塔顶端C的仰角为60°,CD⊥AB与点E,E、B、A在一条直线上.请你帮李明同学计算出信号塔CD的高度(结果保留整数,≈1.7,≈1.4 )
25.【问题提出】
(1)如图①,为半圆的直径,O为圆心,C,D为半圆上的两点,若,,则___.
【问题探究】
(2)如图②,在矩形中,,,点P在直线的右侧,且满足,求点P到的最短距离.
【问题解决】
(3)如图③,有一块矩形型板材,米,米,由于工作需要,工人王师傅想在这块板材上找一点P,裁出与,并满足,.请问王师傅的设想可以实现吗?如果可以,请帮他计算所裁得的的面积;如果不能,请说明你的理由.
答案解析部分
1.【答案】4.1
【知识点】解直角三角形的其他实际应用
2.【答案】
【知识点】三角形内角和定理;求特殊角的三角函数值;绝对值的非负性
3.【答案】
【知识点】解直角三角形;正多边形的性质
4.【答案】
【知识点】完全平方公式及运用;同角三角函数的关系
5.【答案】
【知识点】正方形的性质;圆内接正多边形;解直角三角形;旋转的性质
6.【答案】或
【知识点】勾股定理;矩形的判定与性质;正方形的性质;圆周角定理;锐角三角函数的定义
7.【答案】D
【知识点】解直角三角形的实际应用﹣方向角问题
8.【答案】D
【知识点】求特殊角的三角函数值
9.【答案】C
【知识点】锐角三角函数的定义
10.【答案】D
【知识点】求特殊角的三角函数值
11.【答案】A
【知识点】求特殊角的三角函数值
12.【答案】D
【知识点】求特殊角的三角函数值
13.【答案】C
【知识点】解直角三角形
14.【答案】B
【知识点】平行线之间的距离;正方形的性质;锐角三角函数的定义;三角形全等的判定-AAS
15.【答案】B
【知识点】勾股定理;正方形的性质;解直角三角形
16.【答案】D
【知识点】二次函数图象的几何变换;等腰三角形的性质;锐角三角函数的增减性
17.【答案】(1)cm;(2)9.2cm.
【知识点】解直角三角形的其他实际应用
18.【答案】解:根据题意可知:∠BAD=45°,∠BCD=30°,AC=20m
在Rt△ABD中,由∠BAD=∠BDA=45°,得AB=BD
在Rt△BDC中,由tan∠BCD= ,得
又∵BC-AB=AC,∴ ,∴
答:该古塔BD的高度 m
【知识点】解直角三角形的其他实际应用
19.【答案】解:过点作,垂足为.
,
四边形是矩形,.
由题意知:,
.
设
在中
在中,,
答:纪念碑主碑的高度约为12.5米.
【知识点】解直角三角形的实际应用﹣仰角俯角问题
20.【答案】解:作 于点 ,设 米,
在 中, ,
则 (米 ,
∵ ,且AE=8
∴
∴
在直角 中, 米,
在直角 中, ,
米.
,即 .
解得: ,
则 米.
答: 的高度是 米.
【知识点】解直角三角形的实际应用﹣仰角俯角问题
21.【答案】解:连接,作于D,
∵,,
∴是边边上的中线,也是的角平分线,
∴,,
在中,,,
∴,
∴
∴
答:A,B两点间的距离为.
【知识点】等腰三角形的性质;解直角三角形的其他实际应用
22.【答案】(1)
(2)存在,点坐标为(,)
(3)
【知识点】反比例函数与一次函数的交点问题;两点之间线段最短;锐角三角函数的定义
23.【答案】3
【知识点】零指数幂;负整数指数幂;求特殊角的三角函数值
24.【答案】约为5米.
【知识点】解直角三角形的实际应用﹣仰角俯角问题
25.【答案】(1);(2);(3)师傅的设想可以实现,平方米
【知识点】矩形的性质;圆周角定理;相似三角形的判定与性质;解直角三角形
21世纪教育网(www.21cnjy.com)
2 / 11
第28章锐角三角函数综合检测题
一、填空题
1.某数学兴趣小组测量校园内一棵树的高度,采用以下方法:如图,把支架放在离树适当距离的水平地面上的点F处,再把镜子水平放在支架上的点E处,然后沿着直线后退至点D处,这时恰好在镜子里看到树的顶端A,再用皮尺分别测量,,观测者目高的长,利用测得的数据可以求出这棵树的高度.已知于点D,于点F,于点B,米,米,米,米,则这棵树的高度(的长)是 米.
2.在中,已知,是锐角,若,则的度数为 .
3.如图所示,拧开一个边长为的正六角形螺帽时,扳手张开的开口,则边长 .
4.已知 ,则 = .
5.如图,边长为3的正方形ABCD在正六边形外部做顺时针方向的滚动运动,滚动一周回到初始位置时停止,点A在滚动过程中到出发点的最大距离是 .
6.如图,四边形为正方形,且边长,点是以为直径的圆上一动点,当时,的长度为 .
二、单选题
7.某区域平面示意图如图,点O在河的一侧,和表示两条互相垂直的公路.甲侦测员在处测得点位于北偏东,乙勘测员在处测得点位于南偏西,测得,,请求出点到的距离( ).(参考数据,,)
A.140 B.340 C.360 D.480
8.tan45°的值等于( )
A.2 B. C.-1 D.1
9.如图,△ABC的顶点都在正方形网格的格点上,则tanA的值是( )
A. B. C. D.2
10. 的值等于( )
A.1 B. C. D.
11.如图,在一个直角三角板ABC中, ∠A=60°,则cosA的值为 ( )
A. B.1 C. D.
12. ( )
A. B. C. D.
13.如图所示,是由小正方形构成的网格,每个小正方形的顶点叫做格点,点,,,,均在格点上,则和的大小关系为( )
A. B.
C. D.无法确定
14.如图是墙壁上在l1,l2两条平行线间边长为a的正方形瓷砖,该瓷砖与平行线的较大夹角为a,则两条平行线间的距离为( )
A.asinα B.asinα+acosα
C.2acosα D.asinα﹣acosα
15.如图,,点在上,且,是上的点,在上找点,以为边,, ,为顶点作正方形,则的长不可能是( )
A. B. C. D.
16.如图,抛物线y=-x2+k与x轴交于A(-3,0)和B(3,0),有一动点C在线段AB上从点A运动到点B(不与A,B重合),分别以AC,BC为底边作等腰△ADC和等腰△BEC,点D,E恰好落在此抛物线上,在整个运动过程中, ∠DCE的变化情况是( )
A.保持不变 B.一直减小
C.先增大后减小 D.先减小后增大
三、解答题
17.某电脑桌生产厂家生产了一种平板电脑桌,其实物图如图1所示,此电脑桌的桌面可调节,图2和图3是其调节桌面的侧面示意图,在点C处安装一根长度一定的支撑杆CB,且AC=BC=20cm,点B可在AD上滑动,当B滑动到D处,电脑的承载面AE与AD重合.
(1)如图2,当BC⊥AC时,求电脑的承载面最高点E与B之间的距离;
(2)如图3,小华经过多次试验发现,当∠A=40°时,利用平板电脑观看电影的效果最好,求此时点B与点D之间的距离(参考数据:sin40°≈0.64, cos40°≈0.77, tan40°≈0.84, 结果精确到0.1cm).
18.如图,某校数学兴趣小组的同学欲测量一座垂直于地面的古塔BD的高度,他们先在A处测得古塔顶端点D的仰角为45°,再沿着BA的方向后退20m至C处,测得古塔顶端点D的仰角为30°.求该古塔BD的高度( ,结果保留一位小数).
19.塔山阻击战革命烈士纪念碑(图1)位于葫芦岛市区以东12公里的连山区塔山乡塔山村,是“全国爱国主义教育示范基地”.某校“综合与实践”活动小组借助无人机测量纪念碑主碑的高度.如图2,先将无人机升至距离地面10米高的点处,测得主碑最高点的仰角为,再将无人机从点处竖直向上升高至距离地面15.8米高的点处,测得点的俯角为,已知点在同一平面内,求纪念碑主碑的高度.(结果精确到0.1米)
(参考数据:)
20.在一次课外活动中,某数学兴趣小组测量一棵树 的高度.如图所示,测得斜坡 的坡度 ,坡底 的长为8米,在 处测得树 顶部 的仰角为 ,在 处测得树 顶部 的仰角为 ,求树高 .(结果保留根号)
21.2023年5月30日,神舟十六号载人飞船发射取得圆满成功,3名航天员顺利进驻中国空间站,如图中的照片展示了中国空间站上机械臂的一种工作状态,当两臂,两臂夹角时,求A,B两点间的距离.(结果精确到,参考数据,,)
22.如图,直线与轴交于点,与反比例函数,过作轴于点,且.
(1)求反比例函数表达式;
(2)点是反比例函数图象上的点,在轴上是否存在点,使得最小?若存在,求出点的坐标;若不存在,请说明理由;
(3)将直线向下平移个单位后与反比例函数的图象交于一点,求的值.
四、计算题
23.计算:.
24.如图,在一个18米高的楼顶上有一信号塔DC,李明同学为了测量信号塔的高度,在地面的A处测的信号塔下端D的仰角为30°,然后他正对塔的方向前进了18米到达地面的B处,又测得信号塔顶端C的仰角为60°,CD⊥AB与点E,E、B、A在一条直线上.请你帮李明同学计算出信号塔CD的高度(结果保留整数,≈1.7,≈1.4 )
25.【问题提出】
(1)如图①,为半圆的直径,O为圆心,C,D为半圆上的两点,若,,则___.
【问题探究】
(2)如图②,在矩形中,,,点P在直线的右侧,且满足,求点P到的最短距离.
【问题解决】
(3)如图③,有一块矩形型板材,米,米,由于工作需要,工人王师傅想在这块板材上找一点P,裁出与,并满足,.请问王师傅的设想可以实现吗?如果可以,请帮他计算所裁得的的面积;如果不能,请说明你的理由.
答案解析部分
1.【答案】4.1
【知识点】解直角三角形的其他实际应用
2.【答案】
【知识点】三角形内角和定理;求特殊角的三角函数值;绝对值的非负性
3.【答案】
【知识点】解直角三角形;正多边形的性质
4.【答案】
【知识点】完全平方公式及运用;同角三角函数的关系
5.【答案】
【知识点】正方形的性质;圆内接正多边形;解直角三角形;旋转的性质
6.【答案】或
【知识点】勾股定理;矩形的判定与性质;正方形的性质;圆周角定理;锐角三角函数的定义
7.【答案】D
【知识点】解直角三角形的实际应用﹣方向角问题
8.【答案】D
【知识点】求特殊角的三角函数值
9.【答案】C
【知识点】锐角三角函数的定义
10.【答案】D
【知识点】求特殊角的三角函数值
11.【答案】A
【知识点】求特殊角的三角函数值
12.【答案】D
【知识点】求特殊角的三角函数值
13.【答案】C
【知识点】解直角三角形
14.【答案】B
【知识点】平行线之间的距离;正方形的性质;锐角三角函数的定义;三角形全等的判定-AAS
15.【答案】B
【知识点】勾股定理;正方形的性质;解直角三角形
16.【答案】D
【知识点】二次函数图象的几何变换;等腰三角形的性质;锐角三角函数的增减性
17.【答案】(1)cm;(2)9.2cm.
【知识点】解直角三角形的其他实际应用
18.【答案】解:根据题意可知:∠BAD=45°,∠BCD=30°,AC=20m
在Rt△ABD中,由∠BAD=∠BDA=45°,得AB=BD
在Rt△BDC中,由tan∠BCD= ,得
又∵BC-AB=AC,∴ ,∴
答:该古塔BD的高度 m
【知识点】解直角三角形的其他实际应用
19.【答案】解:过点作,垂足为.
,
四边形是矩形,.
由题意知:,
.
设
在中
在中,,
答:纪念碑主碑的高度约为12.5米.
【知识点】解直角三角形的实际应用﹣仰角俯角问题
20.【答案】解:作 于点 ,设 米,
在 中, ,
则 (米 ,
∵ ,且AE=8
∴
∴
在直角 中, 米,
在直角 中, ,
米.
,即 .
解得: ,
则 米.
答: 的高度是 米.
【知识点】解直角三角形的实际应用﹣仰角俯角问题
21.【答案】解:连接,作于D,
∵,,
∴是边边上的中线,也是的角平分线,
∴,,
在中,,,
∴,
∴
∴
答:A,B两点间的距离为.
【知识点】等腰三角形的性质;解直角三角形的其他实际应用
22.【答案】(1)
(2)存在,点坐标为(,)
(3)
【知识点】反比例函数与一次函数的交点问题;两点之间线段最短;锐角三角函数的定义
23.【答案】3
【知识点】零指数幂;负整数指数幂;求特殊角的三角函数值
24.【答案】约为5米.
【知识点】解直角三角形的实际应用﹣仰角俯角问题
25.【答案】(1);(2);(3)师傅的设想可以实现,平方米
【知识点】矩形的性质;圆周角定理;相似三角形的判定与性质;解直角三角形
21世纪教育网(www.21cnjy.com)
2 / 11
