第29章 投影与视图综合检测题(含答案)
文档属性
| 名称 | 第29章 投影与视图综合检测题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 322.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-27 14:11:56 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第29章 投影与视图综合检测题
一、填空题
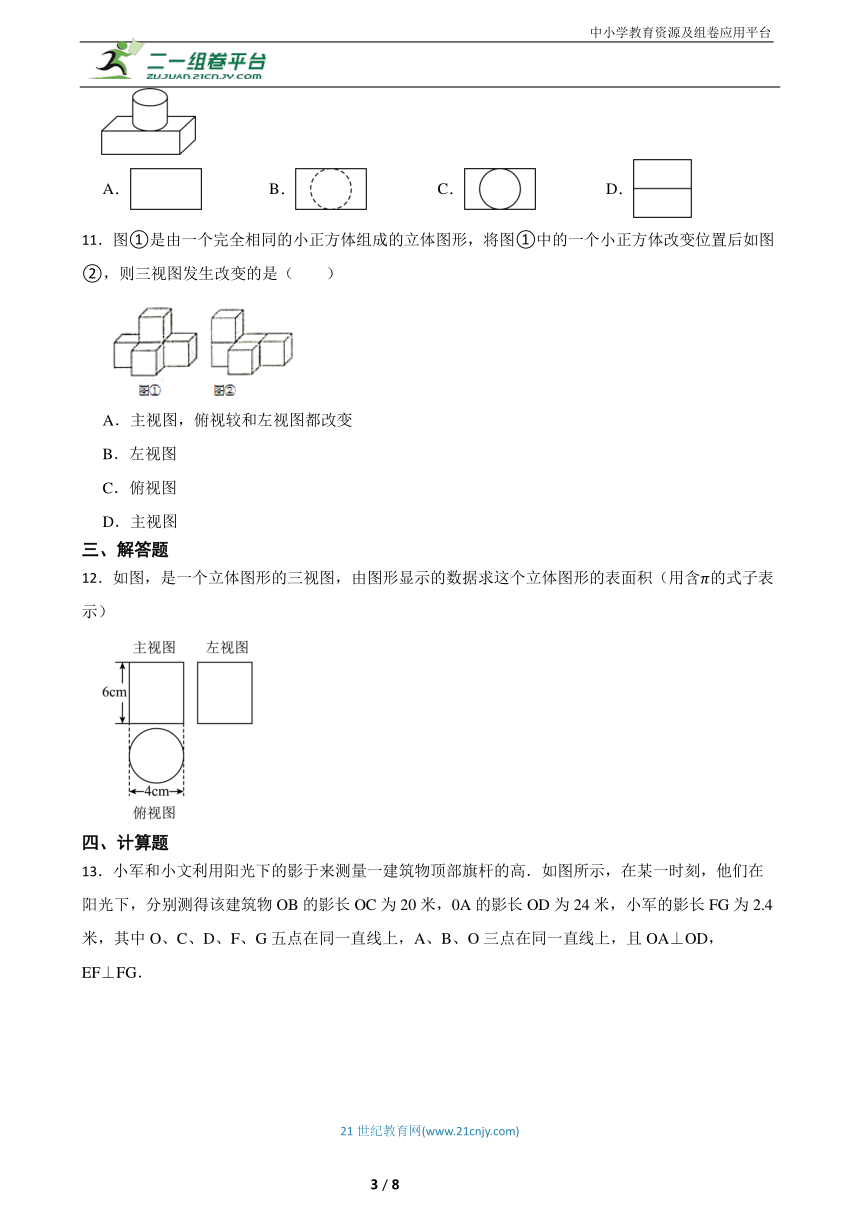
1.由一些完全相同的小正方体组成的几何体的主视图和俯视图如图所示,则组成这个几何体的小正方体的个数可能是 .
2.长方体纸盒的长、宽、高分别是5、4、2,若将它沿棱剪开,展成一个平面图形那么这个平面图形的周长的最小值是 .
3.小林同学在立方体盒子的每个面上都写了一个字,分别是我、喜、欢、数、学、课,其平面展开图如图所示,那么该立方体盒子上,“我”相对的面上所写的文字是 .
4.生活中有这样一种几何体,三视图中至少有二种视图(左、主、俯视图中任意二个视图)是相同的,请你至少写出二种符合要求的几何体: .
5.如图是某个几何体的展开图,写出该几何体的名称 。
6.如图,是一个正方体的表面展开图,则原正方体中与“战”字所在的面相对的面上标的字是 .
二、单选题
7.小明从正面观察下图所示的两个物体,看到的是( )
A. B.
C. D.
8. 如图,将一个正方体沿图示四条棱的中点切掉一部分,则该几何体的俯视图是( )
A. B. C. D.
9.如图,由5个完全一样的小正方体组成的几何体的左视图是( )
A. B.
C. D.
10.如图所放置的物体的俯视图是( )
A. B. C. D.
11.图①是由一个完全相同的小正方体组成的立体图形,将图①中的一个小正方体改变位置后如图②,则三视图发生改变的是( )
A.主视图,俯视较和左视图都改变
B.左视图
C.俯视图
D.主视图
三、解答题
12.如图,是一个立体图形的三视图,由图形显示的数据求这个立体图形的表面积(用含的式子表示)
四、计算题
13.小军和小文利用阳光下的影于来测量一建筑物顶部旗杆的高.如图所示,在某一时刻,他们在阳光下,分别测得该建筑物OB的影长OC为20米,0A的影长OD为24米,小军的影长FG为2.4米,其中O、C、D、F、G五点在同一直线上,A、B、O三点在同一直线上,且OA⊥OD,EF⊥FG.
(1)①图中阳光下的影子属于 (填“中心投影”或“平行投影”)②线段AD、线段BC与线段EG之间的位置关系为 .
(2)已知小军的身高E为1.8米,求旗杆的高AB.
五、作图题
14.画出如图的几何体的主视图、左视图和俯视图.
六、综合题
15.如图,文文应用所学的三角形相关知识测量河南广播电视塔的高度,她站在距离塔底A点处的D点,测得自己的影长DE为,此时该塔的影子为,她测得点D与点C的距离为,已知文文的身高DF为,求河南广播电视塔的高.(图中各点都在同一平面内,点A,C,D,E在同一直线上)
16.如图是一个正方体的表面展开图,请回答下列问题:
(1)与面B、C相对的面分别是
(2)若A=a3+a2b+3,B=a2b-3,C=a3-1,D=-(a2b-6),且相对两个面所表示的代数式的和都相等,求E、F分别代表的代数式.
17.如图①,大风阁是西安汉城湖的标志性建筑,取意于汉高祖刘邦的《大风歌》“大风起兮云飞扬,威加海内兮归故乡,安得猛士兮守四方”的意境.小华和晓丽在一个阳光明媚的周末去测量大风阁的高度,如图②,首先,在C处放置一面平面镜,小华沿着的方向后退,到点E处恰好在平面镜中看到大风阁顶端A的像,小华的眼睛到地面的距离米,米;然后,某一时刻大风阁在阳光下的影子顶端在M处,同时,晓丽测得小华身高的影长米,小华的身高米,米,已知,,点B、M、C、E、G在同一水平直线上,点E、D、F在一条直线上,请你求出大风阁的高度.(平面镜大小、厚度忽略不计)
七、实践探究题
18.【综合实践】
主题:制作一个有盖长方体盒子.
操作:如图甲所示,在长方形纸片中,厘米,厘米,剪掉阴影部分后,剩下的纸片可折成一个底面是正方形的有盖长方体盒子;如图乙所示,在长方体的一个侧面上,分别在边上取两点,测量得:,,,已知侧面四个角都是直角.
计算:
(1)求这个盒子的高和底面正方形的边长;
(2)求的度数.
答案解析部分
1.【答案】4或5(答对一个得1分,多答不得分)
【知识点】由三视图判断几何体
2.【答案】42
【知识点】几何体的展开图
3.【答案】“学”
【知识点】几何体的展开图
4.【答案】足球,碗
【知识点】简单几何体的三视图
5.【答案】圆柱(体)
【知识点】几何体的展开图
6.【答案】冠
【知识点】几何体的展开图
7.【答案】C
【知识点】简单组合体的三视图
8.【答案】C
【知识点】简单几何体的三视图
9.【答案】B
【知识点】简单组合体的三视图
10.【答案】C
【知识点】简单组合体的三视图
11.【答案】D
【知识点】简单几何体的三视图
12.【答案】 cm2
【知识点】由三视图判断几何体;已知三视图进行几何体的相关计算
13.【答案】(1)①平行投影;②(或答“平行”)
(2)旗杆AB的长为3米
【知识点】相似三角形的判定与性质;平行投影
14.【答案】解:如下图所示
【知识点】简单组合体的三视图
15.【答案】
【知识点】相似三角形的应用;平行投影
16.【答案】(1)F、E
(2)解:因为A的对面是D,且a3+a2b+3+[- (a2b-6) ]=a3+9.
所以C的对而E=a3+9- (a3-1) =10.
B的对面F=a3+9- (a2b-3) =a3-a2b+12.
【知识点】几何体的展开图
17.【答案】64米
【知识点】相似三角形的应用;平行投影
18.【答案】(1)这个盒子的高为10厘米,底面正方形的边长为20厘米
(2)
【知识点】几何体的展开图;平行线的判定与性质
21世纪教育网(www.21cnjy.com)
2 / 8
第29章 投影与视图综合检测题
一、填空题
1.由一些完全相同的小正方体组成的几何体的主视图和俯视图如图所示,则组成这个几何体的小正方体的个数可能是 .
2.长方体纸盒的长、宽、高分别是5、4、2,若将它沿棱剪开,展成一个平面图形那么这个平面图形的周长的最小值是 .
3.小林同学在立方体盒子的每个面上都写了一个字,分别是我、喜、欢、数、学、课,其平面展开图如图所示,那么该立方体盒子上,“我”相对的面上所写的文字是 .
4.生活中有这样一种几何体,三视图中至少有二种视图(左、主、俯视图中任意二个视图)是相同的,请你至少写出二种符合要求的几何体: .
5.如图是某个几何体的展开图,写出该几何体的名称 。
6.如图,是一个正方体的表面展开图,则原正方体中与“战”字所在的面相对的面上标的字是 .
二、单选题
7.小明从正面观察下图所示的两个物体,看到的是( )
A. B.
C. D.
8. 如图,将一个正方体沿图示四条棱的中点切掉一部分,则该几何体的俯视图是( )
A. B. C. D.
9.如图,由5个完全一样的小正方体组成的几何体的左视图是( )
A. B.
C. D.
10.如图所放置的物体的俯视图是( )
A. B. C. D.
11.图①是由一个完全相同的小正方体组成的立体图形,将图①中的一个小正方体改变位置后如图②,则三视图发生改变的是( )
A.主视图,俯视较和左视图都改变
B.左视图
C.俯视图
D.主视图
三、解答题
12.如图,是一个立体图形的三视图,由图形显示的数据求这个立体图形的表面积(用含的式子表示)
四、计算题
13.小军和小文利用阳光下的影于来测量一建筑物顶部旗杆的高.如图所示,在某一时刻,他们在阳光下,分别测得该建筑物OB的影长OC为20米,0A的影长OD为24米,小军的影长FG为2.4米,其中O、C、D、F、G五点在同一直线上,A、B、O三点在同一直线上,且OA⊥OD,EF⊥FG.
(1)①图中阳光下的影子属于 (填“中心投影”或“平行投影”)②线段AD、线段BC与线段EG之间的位置关系为 .
(2)已知小军的身高E为1.8米,求旗杆的高AB.
五、作图题
14.画出如图的几何体的主视图、左视图和俯视图.
六、综合题
15.如图,文文应用所学的三角形相关知识测量河南广播电视塔的高度,她站在距离塔底A点处的D点,测得自己的影长DE为,此时该塔的影子为,她测得点D与点C的距离为,已知文文的身高DF为,求河南广播电视塔的高.(图中各点都在同一平面内,点A,C,D,E在同一直线上)
16.如图是一个正方体的表面展开图,请回答下列问题:
(1)与面B、C相对的面分别是
(2)若A=a3+a2b+3,B=a2b-3,C=a3-1,D=-(a2b-6),且相对两个面所表示的代数式的和都相等,求E、F分别代表的代数式.
17.如图①,大风阁是西安汉城湖的标志性建筑,取意于汉高祖刘邦的《大风歌》“大风起兮云飞扬,威加海内兮归故乡,安得猛士兮守四方”的意境.小华和晓丽在一个阳光明媚的周末去测量大风阁的高度,如图②,首先,在C处放置一面平面镜,小华沿着的方向后退,到点E处恰好在平面镜中看到大风阁顶端A的像,小华的眼睛到地面的距离米,米;然后,某一时刻大风阁在阳光下的影子顶端在M处,同时,晓丽测得小华身高的影长米,小华的身高米,米,已知,,点B、M、C、E、G在同一水平直线上,点E、D、F在一条直线上,请你求出大风阁的高度.(平面镜大小、厚度忽略不计)
七、实践探究题
18.【综合实践】
主题:制作一个有盖长方体盒子.
操作:如图甲所示,在长方形纸片中,厘米,厘米,剪掉阴影部分后,剩下的纸片可折成一个底面是正方形的有盖长方体盒子;如图乙所示,在长方体的一个侧面上,分别在边上取两点,测量得:,,,已知侧面四个角都是直角.
计算:
(1)求这个盒子的高和底面正方形的边长;
(2)求的度数.
答案解析部分
1.【答案】4或5(答对一个得1分,多答不得分)
【知识点】由三视图判断几何体
2.【答案】42
【知识点】几何体的展开图
3.【答案】“学”
【知识点】几何体的展开图
4.【答案】足球,碗
【知识点】简单几何体的三视图
5.【答案】圆柱(体)
【知识点】几何体的展开图
6.【答案】冠
【知识点】几何体的展开图
7.【答案】C
【知识点】简单组合体的三视图
8.【答案】C
【知识点】简单几何体的三视图
9.【答案】B
【知识点】简单组合体的三视图
10.【答案】C
【知识点】简单组合体的三视图
11.【答案】D
【知识点】简单几何体的三视图
12.【答案】 cm2
【知识点】由三视图判断几何体;已知三视图进行几何体的相关计算
13.【答案】(1)①平行投影;②(或答“平行”)
(2)旗杆AB的长为3米
【知识点】相似三角形的判定与性质;平行投影
14.【答案】解:如下图所示
【知识点】简单组合体的三视图
15.【答案】
【知识点】相似三角形的应用;平行投影
16.【答案】(1)F、E
(2)解:因为A的对面是D,且a3+a2b+3+[- (a2b-6) ]=a3+9.
所以C的对而E=a3+9- (a3-1) =10.
B的对面F=a3+9- (a2b-3) =a3-a2b+12.
【知识点】几何体的展开图
17.【答案】64米
【知识点】相似三角形的应用;平行投影
18.【答案】(1)这个盒子的高为10厘米,底面正方形的边长为20厘米
(2)
【知识点】几何体的展开图;平行线的判定与性质
21世纪教育网(www.21cnjy.com)
2 / 8
