人教版数学九年级下册综合检测题一(含答案)
文档属性
| 名称 | 人教版数学九年级下册综合检测题一(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 471.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-27 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版数学九年级下册综合检测题一
一、填空题
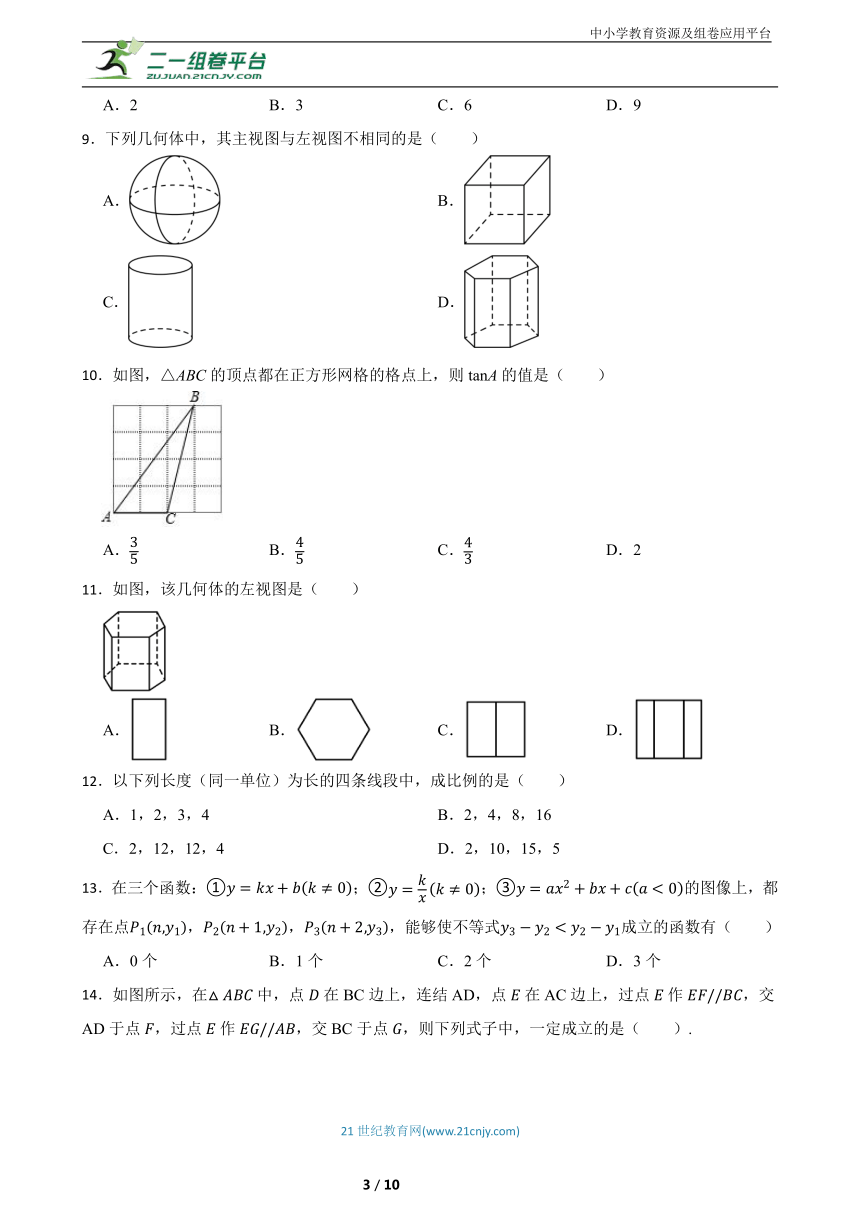
1.如图,在平面直角坐标系中,反比例函数的图像经过点A,点B在x轴上,且,若的面积是5,则 .
2.如图,点是线段的黄金分割点,,和均是等边三角形.若表示的面积,表示的面积,则的值为 ;与的大小关系为 .
3.如图,在平面直角坐标系中,的圆心的坐标为,半径为1,点为直线上的动点,过点作的切线,切点为,则切线长的最小值是 .
4.如图,在平面直角坐标系中,点在反比例函数为常数,,的图象上,过点作轴的垂线,垂足为,连接.若的面积为,则 .
5.如图,在平面直角坐标系中,的斜边的中点与坐标原点重合,点是轴上一点,连接、.若平分,反比例函数的图象经过上的两点、,且,的面积为6,则的值为 .
6.如图,在中,,,,D、F分别是边、上的动点,连接,过点A作交于点E,垂足为G,连接,则的最小值为 .
二、单选题
7.若4m=5n(m≠0),则下列等式成立的是( )
A. B. C. D.
8.如图,,若,,,则的长度是( )
A.2 B.3 C.6 D.9
9.下列几何体中,其主视图与左视图不相同的是( )
A. B.
C. D.
10.如图,△ABC的顶点都在正方形网格的格点上,则tanA的值是( )
A. B. C. D.2
11.如图,该几何体的左视图是( )
A. B. C. D.
12.以下列长度(同一单位)为长的四条线段中,成比例的是( )
A.1,2,3,4 B.2,4,8,16
C.2,12,12,4 D.2,10,15,5
13.在三个函数:①;②;③的图像上,都存在点,,,能够使不等式成立的函数有( )
A.0个 B.1个 C.2个 D.3个
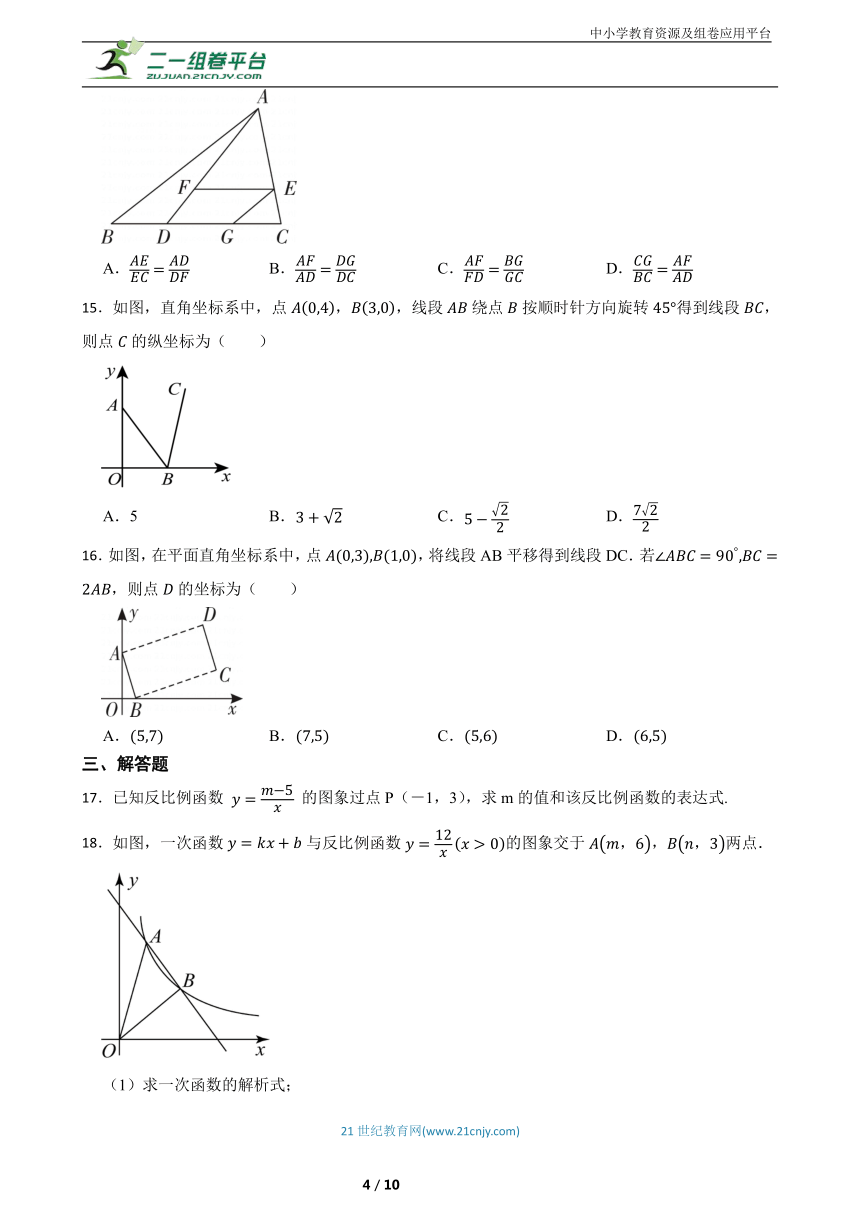
14.如图所示,在中,点在BC边上,连结AD,点在AC边上,过点作,交AD于点,过点作,交BC于点,则下列式子中,一定成立的是( ).
A. B. C. D.
15.如图,直角坐标系中,点,,线段绕点按顺时针方向旋转得到线段,则点的纵坐标为( )
A.5 B. C. D.
16.如图,在平面直角坐标系中,点,将线段AB平移得到线段DC.若,则点的坐标为( )
A. B. C. D.
三、解答题
17.已知反比例函数 的图象过点P(-1,3),求m的值和该反比例函数的表达式.
18.如图,一次函数与反比例函数的图象交于,两点.
(1)求一次函数的解析式;
(2)求的面积.
19.随着科学技术的发展,机器人早已能按照设计的指令完成各种动作.在坐标平面上,根据指令[S,α](S≥0,0°<α<180°)机器人能完成下列动作:先原地顺时针旋转角度α,再朝其对面方向沿直线行走距离s.
(1)如图,若机器人在直角坐标系的原点,且面对y轴的正方向,现要使其移动到点A(2,2),则给机器人发出的指令应是什么;
(2)机器人在完成上述指令后,发现在P(6,0)处有一小球正向坐标原点做匀速直线运动,已知小球滚动的速度与机器人行走的速度相同,若忽略机器人原地旋转的时间,请你给机器人发一个指令,使它能最快截住小球.(如图,点C为机器人最快截住小球的位置,角度精确到度;参考数据:sin49°≈0.75,cos37°≈0.80,tan37°≈0.75)
20.如图,在中,,垂足为点,平分交于点,,,.
(1)求的值;
(2)求线段的长.
21.如图,一次函数的图象与反比例函数的图象交于两点.
(1)求反比例函数的表达式.
(2)求的面积.
22.如图,直线与轴、轴分别交于点、,与反比例函数的图象相交于点和.点为轴上一点,连接,将线段绕点顺时针旋转得到线段.
(1)求与的值;
(2)①点的坐标是______(用含的代数式表示);
②当点落在反比例函数图象上,求的值;
(3)是否存在,使得?若存在,求出的值;若不存在,请说明理由;
(4)当为何值时,的值最小?请直接写出的值.
四、计算题
23.计算:.
24.如图,PA与⊙O相切于A点,弦AB⊥OP,垂足为C,OP与⊙O相交于D点,已知OA=2,OP=4.
(1)求∠POA的度数;
(2)计算弦AB的长.
25.已知:如图,在平面直角坐标系中,为坐标原点,点为轴正半轴上的一个动点,过点的直线与二次函数的图像交于、两点.
(1)若、两点的横坐标分别为、4,求直线的函数关系式;
(2)若,为的中点,且点,求的值;
(3)连接、,若,的面积为1,求点的坐标,
答案解析部分
1.【答案】
【知识点】反比例函数系数k的几何意义
2.【答案】;
【知识点】等边三角形的性质;黄金分割
3.【答案】
【知识点】垂线段最短及其应用;勾股定理;切线的性质;相似三角形的判定与性质
4.【答案】
【知识点】反比例函数系数k的几何意义
5.【答案】-4
【知识点】反比例函数系数k的几何意义;平行线的判定与性质;相似三角形的判定与性质
6.【答案】
【知识点】垂线段最短及其应用;勾股定理;矩形的性质;解直角三角形
7.【答案】B
【知识点】比例的性质
8.【答案】B
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
9.【答案】D
【知识点】简单几何体的三视图
10.【答案】C
【知识点】锐角三角函数的定义
11.【答案】C
【知识点】简单几何体的三视图
12.【答案】B
【知识点】比例线段
13.【答案】B
【知识点】分式的加减法;一次函数的概念;反比例函数的概念;二次函数与一元二次方程的综合应用
14.【答案】C
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
15.【答案】D
【知识点】坐标与图形性质;相似三角形的判定与性质;旋转的性质
16.【答案】D
【知识点】坐标与图形性质;相似三角形的判定与性质
17.【答案】解:把点P(-1,3)代入 ,得 .解得 .
把m=2代入 ,得 ,即 .
∴反比例函数的表达式为 .
【知识点】待定系数法求反比例函数解析式
18.【答案】(1)一次函数的解析式为;
(2)的面积为9.
【知识点】反比例函数与一次函数的交点问题
19.【答案】(1)[2,45°];(2)[2.5,98°].
【知识点】计算器—三角函数;旋转的性质
20.【答案】(1)
(2)
【知识点】等腰三角形的性质;勾股定理;相似三角形的判定与性质;解直角三角形
21.【答案】(1)
(2)8
【知识点】待定系数法求反比例函数解析式;反比例函数与一次函数的交点问题
22.【答案】(1),
(2)①;②或
(3)或
(4)时最小值为
【知识点】反比例函数与一次函数的交点问题;旋转的性质
23.【答案】原式=
【知识点】求特殊角的三角函数值
24.【答案】解:(1)∵PA与⊙O相切于A点,
∴△OAP是直角三角形,
∵OA=2,OP=4,
∴cos∠POA=OA/OP=1/2,
∴∠POA=60°.
(2)∵直角三角形中∠AOC=60°,OA=2,
∴AC=OA×sin60°=2×/2=.
∵AB⊥OP,
∴AB=2AC=2.
【知识点】切线的性质;解直角三角形
25.【答案】(1)
(2)
(3)
【知识点】待定系数法求一次函数解析式;勾股定理;相似三角形的判定与性质
21世纪教育网(www.21cnjy.com)
1 / 10
人教版数学九年级下册综合检测题一
一、填空题
1.如图,在平面直角坐标系中,反比例函数的图像经过点A,点B在x轴上,且,若的面积是5,则 .
2.如图,点是线段的黄金分割点,,和均是等边三角形.若表示的面积,表示的面积,则的值为 ;与的大小关系为 .
3.如图,在平面直角坐标系中,的圆心的坐标为,半径为1,点为直线上的动点,过点作的切线,切点为,则切线长的最小值是 .
4.如图,在平面直角坐标系中,点在反比例函数为常数,,的图象上,过点作轴的垂线,垂足为,连接.若的面积为,则 .
5.如图,在平面直角坐标系中,的斜边的中点与坐标原点重合,点是轴上一点,连接、.若平分,反比例函数的图象经过上的两点、,且,的面积为6,则的值为 .
6.如图,在中,,,,D、F分别是边、上的动点,连接,过点A作交于点E,垂足为G,连接,则的最小值为 .
二、单选题
7.若4m=5n(m≠0),则下列等式成立的是( )
A. B. C. D.
8.如图,,若,,,则的长度是( )
A.2 B.3 C.6 D.9
9.下列几何体中,其主视图与左视图不相同的是( )
A. B.
C. D.
10.如图,△ABC的顶点都在正方形网格的格点上,则tanA的值是( )
A. B. C. D.2
11.如图,该几何体的左视图是( )
A. B. C. D.
12.以下列长度(同一单位)为长的四条线段中,成比例的是( )
A.1,2,3,4 B.2,4,8,16
C.2,12,12,4 D.2,10,15,5
13.在三个函数:①;②;③的图像上,都存在点,,,能够使不等式成立的函数有( )
A.0个 B.1个 C.2个 D.3个
14.如图所示,在中,点在BC边上,连结AD,点在AC边上,过点作,交AD于点,过点作,交BC于点,则下列式子中,一定成立的是( ).
A. B. C. D.
15.如图,直角坐标系中,点,,线段绕点按顺时针方向旋转得到线段,则点的纵坐标为( )
A.5 B. C. D.
16.如图,在平面直角坐标系中,点,将线段AB平移得到线段DC.若,则点的坐标为( )
A. B. C. D.
三、解答题
17.已知反比例函数 的图象过点P(-1,3),求m的值和该反比例函数的表达式.
18.如图,一次函数与反比例函数的图象交于,两点.
(1)求一次函数的解析式;
(2)求的面积.
19.随着科学技术的发展,机器人早已能按照设计的指令完成各种动作.在坐标平面上,根据指令[S,α](S≥0,0°<α<180°)机器人能完成下列动作:先原地顺时针旋转角度α,再朝其对面方向沿直线行走距离s.
(1)如图,若机器人在直角坐标系的原点,且面对y轴的正方向,现要使其移动到点A(2,2),则给机器人发出的指令应是什么;
(2)机器人在完成上述指令后,发现在P(6,0)处有一小球正向坐标原点做匀速直线运动,已知小球滚动的速度与机器人行走的速度相同,若忽略机器人原地旋转的时间,请你给机器人发一个指令,使它能最快截住小球.(如图,点C为机器人最快截住小球的位置,角度精确到度;参考数据:sin49°≈0.75,cos37°≈0.80,tan37°≈0.75)
20.如图,在中,,垂足为点,平分交于点,,,.
(1)求的值;
(2)求线段的长.
21.如图,一次函数的图象与反比例函数的图象交于两点.
(1)求反比例函数的表达式.
(2)求的面积.
22.如图,直线与轴、轴分别交于点、,与反比例函数的图象相交于点和.点为轴上一点,连接,将线段绕点顺时针旋转得到线段.
(1)求与的值;
(2)①点的坐标是______(用含的代数式表示);
②当点落在反比例函数图象上,求的值;
(3)是否存在,使得?若存在,求出的值;若不存在,请说明理由;
(4)当为何值时,的值最小?请直接写出的值.
四、计算题
23.计算:.
24.如图,PA与⊙O相切于A点,弦AB⊥OP,垂足为C,OP与⊙O相交于D点,已知OA=2,OP=4.
(1)求∠POA的度数;
(2)计算弦AB的长.
25.已知:如图,在平面直角坐标系中,为坐标原点,点为轴正半轴上的一个动点,过点的直线与二次函数的图像交于、两点.
(1)若、两点的横坐标分别为、4,求直线的函数关系式;
(2)若,为的中点,且点,求的值;
(3)连接、,若,的面积为1,求点的坐标,
答案解析部分
1.【答案】
【知识点】反比例函数系数k的几何意义
2.【答案】;
【知识点】等边三角形的性质;黄金分割
3.【答案】
【知识点】垂线段最短及其应用;勾股定理;切线的性质;相似三角形的判定与性质
4.【答案】
【知识点】反比例函数系数k的几何意义
5.【答案】-4
【知识点】反比例函数系数k的几何意义;平行线的判定与性质;相似三角形的判定与性质
6.【答案】
【知识点】垂线段最短及其应用;勾股定理;矩形的性质;解直角三角形
7.【答案】B
【知识点】比例的性质
8.【答案】B
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
9.【答案】D
【知识点】简单几何体的三视图
10.【答案】C
【知识点】锐角三角函数的定义
11.【答案】C
【知识点】简单几何体的三视图
12.【答案】B
【知识点】比例线段
13.【答案】B
【知识点】分式的加减法;一次函数的概念;反比例函数的概念;二次函数与一元二次方程的综合应用
14.【答案】C
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
15.【答案】D
【知识点】坐标与图形性质;相似三角形的判定与性质;旋转的性质
16.【答案】D
【知识点】坐标与图形性质;相似三角形的判定与性质
17.【答案】解:把点P(-1,3)代入 ,得 .解得 .
把m=2代入 ,得 ,即 .
∴反比例函数的表达式为 .
【知识点】待定系数法求反比例函数解析式
18.【答案】(1)一次函数的解析式为;
(2)的面积为9.
【知识点】反比例函数与一次函数的交点问题
19.【答案】(1)[2,45°];(2)[2.5,98°].
【知识点】计算器—三角函数;旋转的性质
20.【答案】(1)
(2)
【知识点】等腰三角形的性质;勾股定理;相似三角形的判定与性质;解直角三角形
21.【答案】(1)
(2)8
【知识点】待定系数法求反比例函数解析式;反比例函数与一次函数的交点问题
22.【答案】(1),
(2)①;②或
(3)或
(4)时最小值为
【知识点】反比例函数与一次函数的交点问题;旋转的性质
23.【答案】原式=
【知识点】求特殊角的三角函数值
24.【答案】解:(1)∵PA与⊙O相切于A点,
∴△OAP是直角三角形,
∵OA=2,OP=4,
∴cos∠POA=OA/OP=1/2,
∴∠POA=60°.
(2)∵直角三角形中∠AOC=60°,OA=2,
∴AC=OA×sin60°=2×/2=.
∵AB⊥OP,
∴AB=2AC=2.
【知识点】切线的性质;解直角三角形
25.【答案】(1)
(2)
(3)
【知识点】待定系数法求一次函数解析式;勾股定理;相似三角形的判定与性质
21世纪教育网(www.21cnjy.com)
1 / 10
