六年级数学(人教版)上册第四单元 比培优复习与测试(含答案)
文档属性
| 名称 | 六年级数学(人教版)上册第四单元 比培优复习与测试(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 736.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-26 17:10:59 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
六年级数学(人教版)上册第四单元 培优复习与测试(含答案)
学校:___________姓名:___________班级:___________考号:___________
一、填空题
1.9∶( )==( )∶20==( )(填小数)。
2.一个比的前项是18,后项是10,这个比记作( ),读作( )。
3.把0.4千克∶20克化成最简的整数比是( ),比值是( )。
4.一项工程,甲队独做要10时完成,乙队独做要15时完成,甲乙两队的工作效率比是( ),甲乙两队合做完成这项工程需要( )小时。
5.“二十四节气”准确反映了自然节律变化,作为农耕文明的产物是我国劳动人民的智慧结晶。“夏至”是一年中白天最长的日子,今年“夏至”这天某一地区的白昼和黑夜的时间比大约为7∶5,这一天,该地区黑夜约有( )小时,白昼约有( )小时。
6.甲、乙、丙三个数的平均数是60,甲∶乙∶丙=2∶3∶5,那么甲、乙、丙分别是( )、( )、( )。
7.一种药水,药和水的比是1∶100,那么药占药水的( ),水占药水的( )。
8.《庄子·天下》中有这样一句话:“一尺之棰,日取其半,万世不竭。”意思是说:一尺长的木棒,每天截取一半,永远也截取不完。照这样推算,第三天截取的长度与最初木棒长度的比是( )。
9.右图中阴影部分与空白部分的面积比是( )。
10.甲乙两数的差24,甲乙两数的比是7∶5,则甲数是( ),乙数是( )。
二、选择题
11.甲、乙、丙三人赛跑,甲比乙快,乙比丙慢,甲、乙、丙的速度比是( )。
A.4∶1∶4 B.5∶4∶3 C.15∶12∶16 D.8∶6∶9
12.一个比的比值是,如果前项不变,后项扩大到原数的3倍,这时的比值( )。
A.扩大到原比值的9倍 B.扩大到原比值的3倍
C.缩小到原比值的 D.缩小到原比值的
13.《周髀算经》是中国最古老的天文学和数学著作,其中记载:“勾广三,股修四,径隅五”,意思是:当直角三角形的两条直角边分别为3(勾)和4(股)时,斜边(即最长的边)为5(弦)。后人简单地把这个事实说成“勾3股4弦5”。已知一个直角三角形三条边的长度比是3∶4∶5,且斜边的长度是25cm,则这个直角三角形的周长是( )。
A.15cm B.20cm C.30cm D.60cm
14.将3∶8的前项扩大至原来的2倍,后项缩小至原来的,比值( )。
A.扩大至原来的6倍 B.扩大至原来的1.5倍
C.缩小至原来的 D.缩小至原来的
15.比的前项是0.8,比值是,比的后项是( )。
A. B. C. D.无法确定
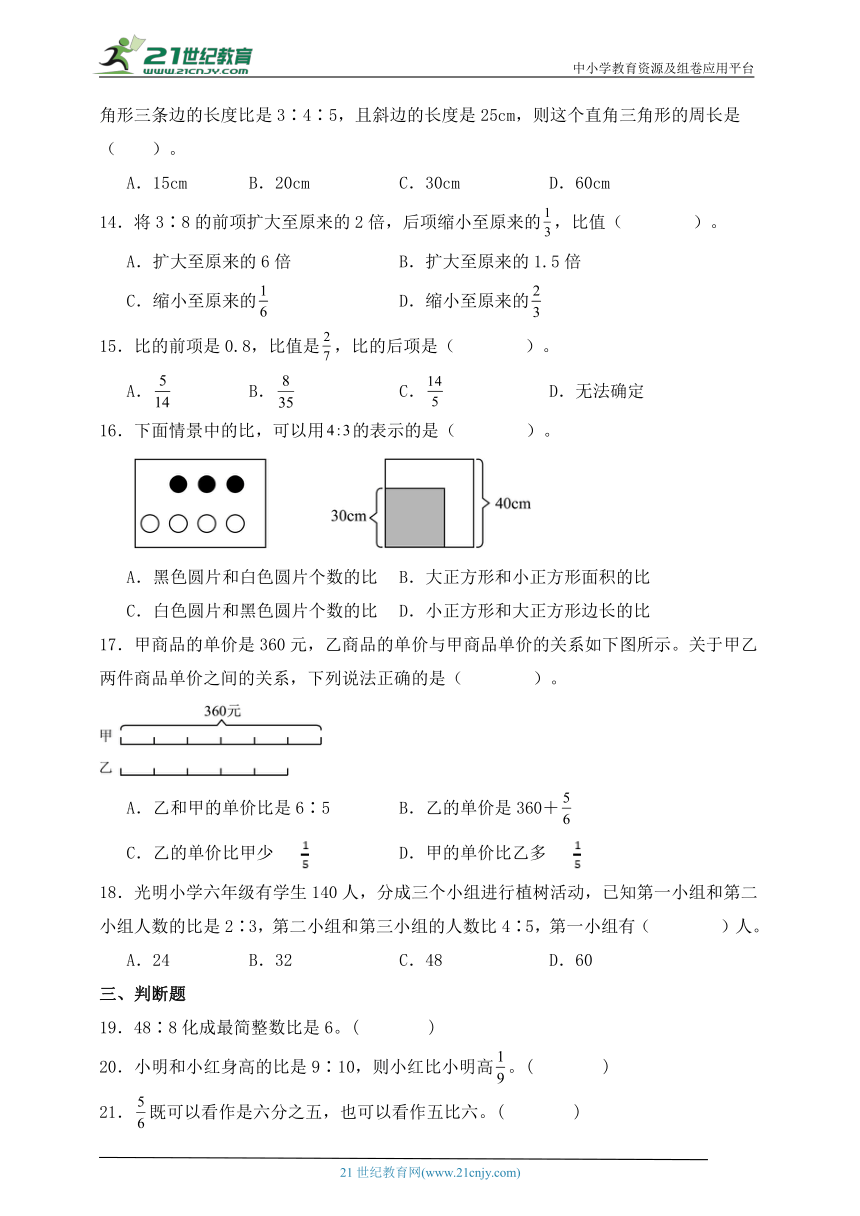
16.下面情景中的比,可以用的表示的是( )。
A.黑色圆片和白色圆片个数的比 B.大正方形和小正方形面积的比
C.白色圆片和黑色圆片个数的比 D.小正方形和大正方形边长的比
17.甲商品的单价是360元,乙商品的单价与甲商品单价的关系如下图所示。关于甲乙两件商品单价之间的关系,下列说法正确的是( )。
A.乙和甲的单价比是6∶5 B.乙的单价是360+
C.乙的单价比甲少 D.甲的单价比乙多
18.光明小学六年级有学生140人,分成三个小组进行植树活动,已知第一小组和第二小组人数的比是2∶3,第二小组和第三小组的人数比4∶5,第一小组有( )人。
A.24 B.32 C.48 D.60
三、判断题
19.48∶8化成最简整数比是6。( )
20.小明和小红身高的比是9∶10,则小红比小明高。( )
21.既可以看作是六分之五,也可以看作五比六。( )
22.比的前项和后项都加上,比值不变。( )
23.如果 a∶b=,那么a一定是2,b一定是3。( )
24.一个三角形三个内角的度数之比是3∶1∶2,这是一个钝角三角形。( )
四、计算题
25.直接写得数。
(求比值)
26.把下面各比化成最简单的整数比。
27.化简比并求比值。
0.42吨∶400千克
五、解答题
28.已知甲、乙是1~100中的两个不相等的自然数,(甲+乙)∶(甲-乙)的比值最大是多少?
29.实验小学女教师人数与男教师人数的比是5∶7,后来调进4名男教师后,女教师人数是男教师的。原来实验小学有男、女教师各多少人?
30.超市运进苹果、香蕉、梨共560千克,苹果与香蕉的质量比是2∶3,香蕉与梨的质量比是4∶5,运进的苹果、香蕉、梨各有多少千克?
31.芳芳利用空余时间折一些千纸鹤,第一天折了总数的,第二天折了70个,这时已折个数与剩下个数的比是3∶5。芳芳一共要折多少个千纸鹤?
32.一种糖是由奶糖、水果糖和酥糖按照4∶3∶2的比例混合而成,现在要配制这种糖450千克,需要奶糖、水果糖和酥糖各多少千克?
33.一辆长途客车只有的座位坐了人,如果再增加6人,则已坐座位和空座位的比是4∶1,这辆客车一共有多少个座位?(用方程解答)
34.某人骑自行车从小镇到县城,8点出发,计划9点到,骑了一段路后,自行车出了故障。下车就地修车10分钟,修车地点距中点还差2千米,他为了按时到县城,车速提高了,结果还是比预定时间晚2分钟到达县城,骑车人原来每小时行多少千米?
参考答案:
1.15;12;40;0.6
2.18∶10 18比10
3.20∶1 20
4.3∶2 6
5.10 14
6.36 54 90
7.
8.1∶8
9.3∶5
10.84 60
11.D
12.C
13.D
14.A
15.C
16.C
17.D
18.B
19.×
20.√
21.√
22.×
23.×
24.×
25.9;;1.5;2.4;;40;;
26.
=(×25)∶(×25)
=2∶20
=(2÷2)∶(20÷2)
=1∶10
0.375∶
=∶
=(×8)∶(×8)
=3∶6
=(3÷3)∶(6÷3)
=1∶2
27.
28.(100+99)∶(100-99)
=199∶1
=199
答:(甲+乙)∶(甲-乙)的比值最大是199。
29.
=
=
=
=40(人)
男教师原来有:40=56(人)
答:原来实验小学有男教师56人,女教师40人。
30.2∶3=(2×4)∶(3×4)=8∶12
4∶5=(4×3)∶(5×3)=12∶15
苹果、香蕉、梨的质量比:8∶12∶15
560÷(8+12+15)
=560÷35
=16(千克)
16×8=128(千克)
16×12=192(千克)
16×15=240(千克)
答:运进的苹果、香蕉、梨各有128千克、192千克、240千克。
31.3+5=8
(个)
答:芳芳一共要折400个千纸鹤。
32.
(千克)
(千克)
(千克)
答:奶糖有200千克,水果糖有150千克,酥糖有100千克。
33.解:这辆客车一共有个座位。
答:这辆客车一共有45个座位。
34.提速后的速度与原来的速度比:
(1+)∶1
=∶1
=(×4)∶(1×4)
=5∶4
提速后用的时间与原来用的时间之比:
(1÷5)∶(1÷4)
=∶
=(×20)∶(×20)
=4∶5
提速前行驶用的时间:
(10-2)÷(5-4)×5
=8÷1×5
=40(分钟)
行驶到故障点的这段路程占全程的:40÷60=
全程:
2÷(-)
=2÷(-)
=2÷
=2×6
=12(千米)
原来每小时行:
12÷(9-8)
=12÷1
=12(千米)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
六年级数学(人教版)上册第四单元 培优复习与测试(含答案)
学校:___________姓名:___________班级:___________考号:___________
一、填空题
1.9∶( )==( )∶20==( )(填小数)。
2.一个比的前项是18,后项是10,这个比记作( ),读作( )。
3.把0.4千克∶20克化成最简的整数比是( ),比值是( )。
4.一项工程,甲队独做要10时完成,乙队独做要15时完成,甲乙两队的工作效率比是( ),甲乙两队合做完成这项工程需要( )小时。
5.“二十四节气”准确反映了自然节律变化,作为农耕文明的产物是我国劳动人民的智慧结晶。“夏至”是一年中白天最长的日子,今年“夏至”这天某一地区的白昼和黑夜的时间比大约为7∶5,这一天,该地区黑夜约有( )小时,白昼约有( )小时。
6.甲、乙、丙三个数的平均数是60,甲∶乙∶丙=2∶3∶5,那么甲、乙、丙分别是( )、( )、( )。
7.一种药水,药和水的比是1∶100,那么药占药水的( ),水占药水的( )。
8.《庄子·天下》中有这样一句话:“一尺之棰,日取其半,万世不竭。”意思是说:一尺长的木棒,每天截取一半,永远也截取不完。照这样推算,第三天截取的长度与最初木棒长度的比是( )。
9.右图中阴影部分与空白部分的面积比是( )。
10.甲乙两数的差24,甲乙两数的比是7∶5,则甲数是( ),乙数是( )。
二、选择题
11.甲、乙、丙三人赛跑,甲比乙快,乙比丙慢,甲、乙、丙的速度比是( )。
A.4∶1∶4 B.5∶4∶3 C.15∶12∶16 D.8∶6∶9
12.一个比的比值是,如果前项不变,后项扩大到原数的3倍,这时的比值( )。
A.扩大到原比值的9倍 B.扩大到原比值的3倍
C.缩小到原比值的 D.缩小到原比值的
13.《周髀算经》是中国最古老的天文学和数学著作,其中记载:“勾广三,股修四,径隅五”,意思是:当直角三角形的两条直角边分别为3(勾)和4(股)时,斜边(即最长的边)为5(弦)。后人简单地把这个事实说成“勾3股4弦5”。已知一个直角三角形三条边的长度比是3∶4∶5,且斜边的长度是25cm,则这个直角三角形的周长是( )。
A.15cm B.20cm C.30cm D.60cm
14.将3∶8的前项扩大至原来的2倍,后项缩小至原来的,比值( )。
A.扩大至原来的6倍 B.扩大至原来的1.5倍
C.缩小至原来的 D.缩小至原来的
15.比的前项是0.8,比值是,比的后项是( )。
A. B. C. D.无法确定
16.下面情景中的比,可以用的表示的是( )。
A.黑色圆片和白色圆片个数的比 B.大正方形和小正方形面积的比
C.白色圆片和黑色圆片个数的比 D.小正方形和大正方形边长的比
17.甲商品的单价是360元,乙商品的单价与甲商品单价的关系如下图所示。关于甲乙两件商品单价之间的关系,下列说法正确的是( )。
A.乙和甲的单价比是6∶5 B.乙的单价是360+
C.乙的单价比甲少 D.甲的单价比乙多
18.光明小学六年级有学生140人,分成三个小组进行植树活动,已知第一小组和第二小组人数的比是2∶3,第二小组和第三小组的人数比4∶5,第一小组有( )人。
A.24 B.32 C.48 D.60
三、判断题
19.48∶8化成最简整数比是6。( )
20.小明和小红身高的比是9∶10,则小红比小明高。( )
21.既可以看作是六分之五,也可以看作五比六。( )
22.比的前项和后项都加上,比值不变。( )
23.如果 a∶b=,那么a一定是2,b一定是3。( )
24.一个三角形三个内角的度数之比是3∶1∶2,这是一个钝角三角形。( )
四、计算题
25.直接写得数。
(求比值)
26.把下面各比化成最简单的整数比。
27.化简比并求比值。
0.42吨∶400千克
五、解答题
28.已知甲、乙是1~100中的两个不相等的自然数,(甲+乙)∶(甲-乙)的比值最大是多少?
29.实验小学女教师人数与男教师人数的比是5∶7,后来调进4名男教师后,女教师人数是男教师的。原来实验小学有男、女教师各多少人?
30.超市运进苹果、香蕉、梨共560千克,苹果与香蕉的质量比是2∶3,香蕉与梨的质量比是4∶5,运进的苹果、香蕉、梨各有多少千克?
31.芳芳利用空余时间折一些千纸鹤,第一天折了总数的,第二天折了70个,这时已折个数与剩下个数的比是3∶5。芳芳一共要折多少个千纸鹤?
32.一种糖是由奶糖、水果糖和酥糖按照4∶3∶2的比例混合而成,现在要配制这种糖450千克,需要奶糖、水果糖和酥糖各多少千克?
33.一辆长途客车只有的座位坐了人,如果再增加6人,则已坐座位和空座位的比是4∶1,这辆客车一共有多少个座位?(用方程解答)
34.某人骑自行车从小镇到县城,8点出发,计划9点到,骑了一段路后,自行车出了故障。下车就地修车10分钟,修车地点距中点还差2千米,他为了按时到县城,车速提高了,结果还是比预定时间晚2分钟到达县城,骑车人原来每小时行多少千米?
参考答案:
1.15;12;40;0.6
2.18∶10 18比10
3.20∶1 20
4.3∶2 6
5.10 14
6.36 54 90
7.
8.1∶8
9.3∶5
10.84 60
11.D
12.C
13.D
14.A
15.C
16.C
17.D
18.B
19.×
20.√
21.√
22.×
23.×
24.×
25.9;;1.5;2.4;;40;;
26.
=(×25)∶(×25)
=2∶20
=(2÷2)∶(20÷2)
=1∶10
0.375∶
=∶
=(×8)∶(×8)
=3∶6
=(3÷3)∶(6÷3)
=1∶2
27.
28.(100+99)∶(100-99)
=199∶1
=199
答:(甲+乙)∶(甲-乙)的比值最大是199。
29.
=
=
=
=40(人)
男教师原来有:40=56(人)
答:原来实验小学有男教师56人,女教师40人。
30.2∶3=(2×4)∶(3×4)=8∶12
4∶5=(4×3)∶(5×3)=12∶15
苹果、香蕉、梨的质量比:8∶12∶15
560÷(8+12+15)
=560÷35
=16(千克)
16×8=128(千克)
16×12=192(千克)
16×15=240(千克)
答:运进的苹果、香蕉、梨各有128千克、192千克、240千克。
31.3+5=8
(个)
答:芳芳一共要折400个千纸鹤。
32.
(千克)
(千克)
(千克)
答:奶糖有200千克,水果糖有150千克,酥糖有100千克。
33.解:这辆客车一共有个座位。
答:这辆客车一共有45个座位。
34.提速后的速度与原来的速度比:
(1+)∶1
=∶1
=(×4)∶(1×4)
=5∶4
提速后用的时间与原来用的时间之比:
(1÷5)∶(1÷4)
=∶
=(×20)∶(×20)
=4∶5
提速前行驶用的时间:
(10-2)÷(5-4)×5
=8÷1×5
=40(分钟)
行驶到故障点的这段路程占全程的:40÷60=
全程:
2÷(-)
=2÷(-)
=2÷
=2×6
=12(千米)
原来每小时行:
12÷(9-8)
=12÷1
=12(千米)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
