14.3.2公式法(1)
图片预览






文档简介
(共17张PPT)
人教版 八年级数学上
14.3.2公式法(1)
学习目标
1.探索平方差公式进行因式分解,体会转化思想.(重点)
2.综合运用提公因式法和平方差公式对多项式进行因式分解.(难点)
温故知新
2.把下列各式因式分解.
1.利用提公因式法分解因式时,如何确定公因式呢?
一看系数(最大公约数),二看字母(相同字母),三看指数(最低指数).
合作探究
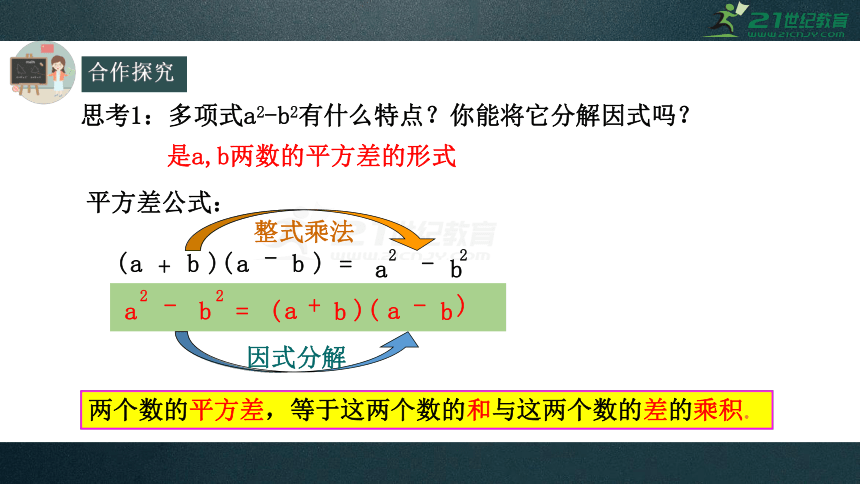
思考1:多项式a2-b2有什么特点?你能将它分解因式吗?
是a,b两数的平方差的形式
)
)(
(
b
a
b
a
-
+
=
2
2
b
a
-
)
)(
(
2
2
b
a
b
a
b
a
-
+
=
-
整式乘法
因式分解
两个数的平方差,等于这两个数的和与这两个数的差的乘积.
平方差公式:
小试牛刀
√
√
×
×
1.下列各式能否用平方差公式来分解因式,为什么?
√
√
(1)x2+y2
(2)x2-y2
(3)-x2-y2
-(x2+y2)
y2-x2
(4)-x2+y2
(5)x2-25y2
(x+5y)(x-5y)
(6)m2-1
(m+1)(m-1)
典例精析
例1.分解因式:
解:
小试牛刀
分解因式:
(1)(a+b)2-9a2; (2)16(m+n)2-(m-n)2.
=(3m+3n)(5m+3n)
解:(1)原式=(a+b-9a)(a+b+9a)
=(b-2a)(10a+b);
(2)原式=(4m+4n-m+n)(4m+4n+m-n)
=3(m+n)(5m+3n).
若用平方差公式分解后的结果中有公因式,一定要再用提公因式法继续分解.
典例精析
例2.分解因式:
解:(1)原式=(x2)2-(y2)2
=(x2+y2)(x2-y2)
分解因式后,一定要检查是否还有能继续分解的因式,若有,则需继续分解.
=(x2+y2)(x+y)(x-y);
(2)原式=ab(a2-1)
分解因式时,一般先用提公因式法进行分解,然后再用公式法.最后进行检查.
=ab(a+1)(a-1).
小试牛刀
1.分解因式:
(1)a2- b2; (2)9a2-4b2;
(3)xy2-4y; (4)-a4+16.
解:(1)原式=(a+ b)(a- b);
(2)原式=(3a+2b)(3a-2b)
(3)原式=x(y+2)(y-2)
(4)原式=x(a2+4)(a-2)(a+2)
小试牛刀
2.已知x2-y2=-8,x+y=2,求x-y,x,y的值.
∴x-y=-4 ②.
解:∵x2-y2=(x+y)(x-y)=-8,
x+y=2 ①,
联立①②组成二元一次方程组,
解得:
x=-1
y=3
小试牛刀
3.求证:当n为整数时,多项式(6n+1)2-(6n-1)2一定能被24整除.
即多项式(3n+1)2-(3n-1)2一定能被24整除.
证明:原式=(6n+1+6n-1)(6n+1-6n+1)=12n 2=24n,
∵n为整数,
∴24n被24整除,
课堂小结
今天我们收获了哪些知识?
1.说一说因式分解的平方差公式?
2.综合运用提公因式法和平方差公式进行因式分解时要注意什么?
a2-b2=(a+b)(a-b)
一提:公因式;二套:公式;
三查:多项式的因式分解有没有分解到不能再分解为止.
实战演练
1.下列分解因式正确的是( )
A.a2-2b2=(a+2b)(a-2b)
B.-x2+y2=(-x+y)(x-y)
C.-a2+4b2=-(a+4b)(a-4b)
D.4x2-0.04y2=(2x+0.2y)(2x-0.2y)
D
实战演练
2.下列多项式中能用平方差公式分解因式的是( )
A.a2+(-2b)2 B.6m2-24mn
C.-x2-4y2 D.-x2+9
D
3.分解因式(2x+3)2 -x2的结果是( )
A.3(x2+4x+3) B.3(x2+2x+3)
C.(3x+3)(x+3) D.3(x+1)(x+3)
D
实战演练
5.已知4m+n=8,2m-3n=5.求(m+2n)2-(3m-n)2的值.
原式=-8×5=-40.
解:原式=(m+2n+3m-n)(m+2n-3m+n)
=(4m+n)(3n-2m)
=-(4m+n)(2m-3n),
当4m+n=8,2m-3n=5时,
4.若a+b=4,a-b=6,则b2-a2的值为 .
-24
课后作业
教材119页练习题第2、4(2)题.
https://www.21cnjy.com/help/help_extract.php
人教版 八年级数学上
14.3.2公式法(1)
学习目标
1.探索平方差公式进行因式分解,体会转化思想.(重点)
2.综合运用提公因式法和平方差公式对多项式进行因式分解.(难点)
温故知新
2.把下列各式因式分解.
1.利用提公因式法分解因式时,如何确定公因式呢?
一看系数(最大公约数),二看字母(相同字母),三看指数(最低指数).
合作探究
思考1:多项式a2-b2有什么特点?你能将它分解因式吗?
是a,b两数的平方差的形式
)
)(
(
b
a
b
a
-
+
=
2
2
b
a
-
)
)(
(
2
2
b
a
b
a
b
a
-
+
=
-
整式乘法
因式分解
两个数的平方差,等于这两个数的和与这两个数的差的乘积.
平方差公式:
小试牛刀
√
√
×
×
1.下列各式能否用平方差公式来分解因式,为什么?
√
√
(1)x2+y2
(2)x2-y2
(3)-x2-y2
-(x2+y2)
y2-x2
(4)-x2+y2
(5)x2-25y2
(x+5y)(x-5y)
(6)m2-1
(m+1)(m-1)
典例精析
例1.分解因式:
解:
小试牛刀
分解因式:
(1)(a+b)2-9a2; (2)16(m+n)2-(m-n)2.
=(3m+3n)(5m+3n)
解:(1)原式=(a+b-9a)(a+b+9a)
=(b-2a)(10a+b);
(2)原式=(4m+4n-m+n)(4m+4n+m-n)
=3(m+n)(5m+3n).
若用平方差公式分解后的结果中有公因式,一定要再用提公因式法继续分解.
典例精析
例2.分解因式:
解:(1)原式=(x2)2-(y2)2
=(x2+y2)(x2-y2)
分解因式后,一定要检查是否还有能继续分解的因式,若有,则需继续分解.
=(x2+y2)(x+y)(x-y);
(2)原式=ab(a2-1)
分解因式时,一般先用提公因式法进行分解,然后再用公式法.最后进行检查.
=ab(a+1)(a-1).
小试牛刀
1.分解因式:
(1)a2- b2; (2)9a2-4b2;
(3)xy2-4y; (4)-a4+16.
解:(1)原式=(a+ b)(a- b);
(2)原式=(3a+2b)(3a-2b)
(3)原式=x(y+2)(y-2)
(4)原式=x(a2+4)(a-2)(a+2)
小试牛刀
2.已知x2-y2=-8,x+y=2,求x-y,x,y的值.
∴x-y=-4 ②.
解:∵x2-y2=(x+y)(x-y)=-8,
x+y=2 ①,
联立①②组成二元一次方程组,
解得:
x=-1
y=3
小试牛刀
3.求证:当n为整数时,多项式(6n+1)2-(6n-1)2一定能被24整除.
即多项式(3n+1)2-(3n-1)2一定能被24整除.
证明:原式=(6n+1+6n-1)(6n+1-6n+1)=12n 2=24n,
∵n为整数,
∴24n被24整除,
课堂小结
今天我们收获了哪些知识?
1.说一说因式分解的平方差公式?
2.综合运用提公因式法和平方差公式进行因式分解时要注意什么?
a2-b2=(a+b)(a-b)
一提:公因式;二套:公式;
三查:多项式的因式分解有没有分解到不能再分解为止.
实战演练
1.下列分解因式正确的是( )
A.a2-2b2=(a+2b)(a-2b)
B.-x2+y2=(-x+y)(x-y)
C.-a2+4b2=-(a+4b)(a-4b)
D.4x2-0.04y2=(2x+0.2y)(2x-0.2y)
D
实战演练
2.下列多项式中能用平方差公式分解因式的是( )
A.a2+(-2b)2 B.6m2-24mn
C.-x2-4y2 D.-x2+9
D
3.分解因式(2x+3)2 -x2的结果是( )
A.3(x2+4x+3) B.3(x2+2x+3)
C.(3x+3)(x+3) D.3(x+1)(x+3)
D
实战演练
5.已知4m+n=8,2m-3n=5.求(m+2n)2-(3m-n)2的值.
原式=-8×5=-40.
解:原式=(m+2n+3m-n)(m+2n-3m+n)
=(4m+n)(3n-2m)
=-(4m+n)(2m-3n),
当4m+n=8,2m-3n=5时,
4.若a+b=4,a-b=6,则b2-a2的值为 .
-24
课后作业
教材119页练习题第2、4(2)题.
https://www.21cnjy.com/help/help_extract.php
