人教版数学九年级上册·下册综合复习题一(含答案)
文档属性
| 名称 | 人教版数学九年级上册·下册综合复习题一(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-27 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版数学九年级上册·下册综合复习题一(精华)
一、填空题
1.将抛物线先向右平移1个单位长度,再向上平移2个单位长度,得到的新抛物线的函数表达式为 .
2.已知是二次函数,则m的值为 .
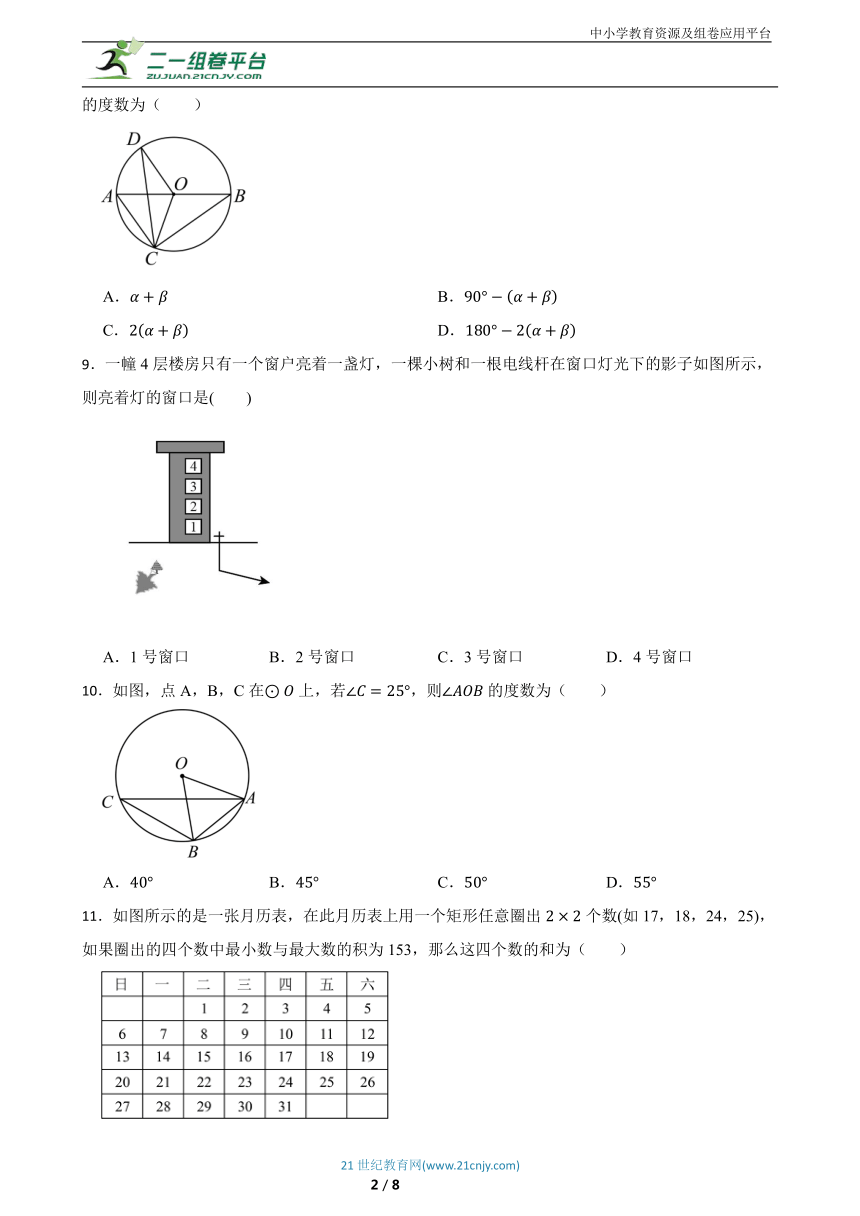
3.“水幕电影”的工作原理是把影像打在抛物线状的水幕上,通过光学原理折射出图像,水幕是由若干个水嘴喷出的水柱组成的(如图),水柱的最高点为P,m,m,水嘴高m,则水柱落地点C到水嘴所在墙的距离是 m.
4.如图,已知,,,以为圆心,为半径作,与线段有交点时,则的取值范围是 .
5.写出方程的解 .
6.已知,则.
二、单选题
7.如图,直线是的边的垂直平分线,平分,若,,则的长为( )
A.3 B.4 C.5 D.6
8.如图,是的直径,、为圆上两点,连接、、,若,,则的度数为( )
A. B.
C. D.
9.一幢4层楼房只有一个窗户亮着一盏灯,一棵小树和一根电线杆在窗口灯光下的影子如图所示,则亮着灯的窗口是( )
A.1号窗口 B.2号窗口 C.3号窗口 D.4号窗口
10.如图,点A,B,C在上,若,则的度数为( )
A. B. C. D.
11.如图所示的是一张月历表,在此月历表上用一个矩形任意圈出个数(如17,18,24,25),如果圈出的四个数中最小数与最大数的积为153,那么这四个数的和为( )
A.40 B.48 C.52 D.56
三、解答题
12.解方程:
(1)
(2)
四、判断题
判断:下列事件中,哪些事件发生的可能性是相同的 相同的画“√”,不相同的画“×”.
13.掷一枚质地均匀的骰子,出现1点或5点朝上的可能性.( )
14.从装有5个红球、3个白球的袋中任取一球,取到红球或白球的可能性. ( )
15.从一副扑克牌中任取一张,取到小王或黑桃5的可能性.( )
16.掷两枚质地均匀的骰子,出现的点数和是“2”或“5”的可能性.( )
17.盒子中有3个红球和2个白球,球除颜色外完全相同,从中任意摸出一个球,摸红球的可能性大.
18.投掷3次硬币,有2次正面朝上,1次反面朝上,那么,投掷第4次硬币正面朝上的可能性是.
19.线段是中心对称图形,对称中心是它的中点。
20.袋子里有同样多的红球和黄球,摸10次,摸到黄球的次数有可能比红球多.
五、计算题
21.解方程:
22.筒车是我国古代利用水力驱动的灌溉工具,唐代陈廷章在《水轮赋》中写道:“水能利物,轮乃曲成”.如图,半径为的筒车按逆时针方向每分钟转圈,筒车与水面分别交于点、,筒车的轴心距离水面的高度长为,筒车上均匀分布着若干个盛水筒.若以某个盛水筒刚浮出水面时开始计算时间.
(1)经过多长时间,盛水筒首次到达最高点?
(2)浮出水面3.4秒后,盛水筒距离水面多高?
(3)若接水槽所在直线是的切线,且与直线交于点,.求盛水筒从最高点开始,至少经过多长时间恰好在直线上.(参考数据:,,)
23.如图、在平面直角坐标系中,抛物线经过点.点A在抛物线上,点A的横坐标为m.点C的坐标为,以为对角线作矩形,使轴.
(1)求抛物线所对应的函数解析式;
(2)求抛物线与y轴的交点坐标;
(3)当时,求抛物线在矩形内部的图象(包含边界)的最大值与最小值的差;
(4)当抛物线与矩形的边恰好有4个交点(包含端点)时,直接写出m的取值范围.
六、作图题
24.如图,在的方格中,有4个小方格被涂黑成“L”形.
(1)在图1中再涂黑2格,使新涂黑的图形与原来的“L”形组成的新图形既是轴对称图形又是中心对称图形;
(2)在图2中再涂黑2格,使新涂黑的图形与原来的“L”形组成的新图形是轴对称图形但不是中心对称图形.
七、综合题
25.某商场销售一批衬衫,平均每天可销售出20件,每件盈利50元,为扩大销售盈利,商场决定采取适当的降价措施,但要求每件盈利不少于30元,经调查发现,若每件衬衫每降价5元、则商场每天可多销售10件、若商场平均每天盈利1600元,则每件衬衫应降价多少元?
26.某百货商店服装在销售过程中发现,某品牌童装平均每天可售出20件,每件盈利40元,经市场调查发现,在进货不变的情况下,若每件童装每降价1元,日销售量将增加2件,当每件童装降价多少元时,这种童装一天的销售利润最多?最多利润是多少?
27.2019年在武汉市举行了军运会,在军运会比赛中,某次羽毛球的运动路线可以看作是抛物线(如图),其中出球点B离地面的距离是米,球落点的水平距离是多少?
八、实践探究题
28.在“综合与实践”活动中,某校九年级数学小组采用无人机辅助的方法测量一座桥的长度.如图,桥是水平并且笔直的,测量过程中,小组成员遥控无人机飞到桥的上方90m的点C处悬停,此时测得桥两端A,B两点的俯角分别为60°和45°,求桥的长度.(结果精确到1m.参考数据:,)
答案解析部分
1.【答案】
【知识点】二次函数图象的几何变换
2.【答案】1
【知识点】二次函数的定义
3.【答案】5
【知识点】二次函数的实际应用-喷水问题
4.【答案】
【知识点】含30°角的直角三角形;直线与圆的位置关系
5.【答案】,
【知识点】直接开平方法解一元二次方程
6.【答案】
【知识点】比例的性质
7.【答案】D
【知识点】角平分线的性质;线段垂直平分线的性质;相似三角形的判定与性质
8.【答案】D
【知识点】圆周角定理
9.【答案】B
【知识点】中心投影
10.【答案】C
【知识点】圆周角定理
11.【答案】C
【知识点】一元二次方程的应用-数字问题
12.【答案】(1),
(2),
【知识点】直接开平方法解一元二次方程;因式分解法解一元二次方程
【答案】13.正确
14.错误
15.正确
16.错误
【知识点】可能性的大小
17.【答案】
【知识点】可能性的大小;概率的意义
18.【答案】×
【知识点】可能性的大小
19.【答案】正确
【知识点】中心对称及中心对称图形
20.【答案】√
【知识点】可能性的大小
21.【答案】解:
,
[(x-1)-5][(x-1)+3]=0,
(x-1)-5=0或(x-1)+3=0,
所以x1=6,x2=-2.
【知识点】因式分解法解一元二次方程
22.【答案】(1)27.4秒;(2)0.7m;(3)7.6秒
【知识点】切线的性质;求特殊角的三角函数值;解直角三角形
23.【答案】(1)
(2)
(3)2
(4)或
【知识点】待定系数法求二次函数解析式;二次函数图象与坐标轴的交点问题
24.【答案】(1)如图1,作图不唯一,符合要求即可.
(2)如图2,作图不唯一,符合要求即可.
【知识点】轴对称图形;中心对称及中心对称图形
25.【答案】每件衬衫应降价10元
【知识点】一元二次方程的实际应用-销售问题
26.【答案】每件童装降价15元时,每天销售这种童装的利润最高,最高利润是1250元.
【知识点】二次函数的实际应用-销售问题
27.【答案】5米
【知识点】二次函数的实际应用-抛球问题
28.【答案】桥的长度约为.
【知识点】解直角三角形的实际应用﹣仰角俯角问题
21世纪教育网(www.21cnjy.com)
2 / 8
人教版数学九年级上册·下册综合复习题一(精华)
一、填空题
1.将抛物线先向右平移1个单位长度,再向上平移2个单位长度,得到的新抛物线的函数表达式为 .
2.已知是二次函数,则m的值为 .
3.“水幕电影”的工作原理是把影像打在抛物线状的水幕上,通过光学原理折射出图像,水幕是由若干个水嘴喷出的水柱组成的(如图),水柱的最高点为P,m,m,水嘴高m,则水柱落地点C到水嘴所在墙的距离是 m.
4.如图,已知,,,以为圆心,为半径作,与线段有交点时,则的取值范围是 .
5.写出方程的解 .
6.已知,则.
二、单选题
7.如图,直线是的边的垂直平分线,平分,若,,则的长为( )
A.3 B.4 C.5 D.6
8.如图,是的直径,、为圆上两点,连接、、,若,,则的度数为( )
A. B.
C. D.
9.一幢4层楼房只有一个窗户亮着一盏灯,一棵小树和一根电线杆在窗口灯光下的影子如图所示,则亮着灯的窗口是( )
A.1号窗口 B.2号窗口 C.3号窗口 D.4号窗口
10.如图,点A,B,C在上,若,则的度数为( )
A. B. C. D.
11.如图所示的是一张月历表,在此月历表上用一个矩形任意圈出个数(如17,18,24,25),如果圈出的四个数中最小数与最大数的积为153,那么这四个数的和为( )
A.40 B.48 C.52 D.56
三、解答题
12.解方程:
(1)
(2)
四、判断题
判断:下列事件中,哪些事件发生的可能性是相同的 相同的画“√”,不相同的画“×”.
13.掷一枚质地均匀的骰子,出现1点或5点朝上的可能性.( )
14.从装有5个红球、3个白球的袋中任取一球,取到红球或白球的可能性. ( )
15.从一副扑克牌中任取一张,取到小王或黑桃5的可能性.( )
16.掷两枚质地均匀的骰子,出现的点数和是“2”或“5”的可能性.( )
17.盒子中有3个红球和2个白球,球除颜色外完全相同,从中任意摸出一个球,摸红球的可能性大.
18.投掷3次硬币,有2次正面朝上,1次反面朝上,那么,投掷第4次硬币正面朝上的可能性是.
19.线段是中心对称图形,对称中心是它的中点。
20.袋子里有同样多的红球和黄球,摸10次,摸到黄球的次数有可能比红球多.
五、计算题
21.解方程:
22.筒车是我国古代利用水力驱动的灌溉工具,唐代陈廷章在《水轮赋》中写道:“水能利物,轮乃曲成”.如图,半径为的筒车按逆时针方向每分钟转圈,筒车与水面分别交于点、,筒车的轴心距离水面的高度长为,筒车上均匀分布着若干个盛水筒.若以某个盛水筒刚浮出水面时开始计算时间.
(1)经过多长时间,盛水筒首次到达最高点?
(2)浮出水面3.4秒后,盛水筒距离水面多高?
(3)若接水槽所在直线是的切线,且与直线交于点,.求盛水筒从最高点开始,至少经过多长时间恰好在直线上.(参考数据:,,)
23.如图、在平面直角坐标系中,抛物线经过点.点A在抛物线上,点A的横坐标为m.点C的坐标为,以为对角线作矩形,使轴.
(1)求抛物线所对应的函数解析式;
(2)求抛物线与y轴的交点坐标;
(3)当时,求抛物线在矩形内部的图象(包含边界)的最大值与最小值的差;
(4)当抛物线与矩形的边恰好有4个交点(包含端点)时,直接写出m的取值范围.
六、作图题
24.如图,在的方格中,有4个小方格被涂黑成“L”形.
(1)在图1中再涂黑2格,使新涂黑的图形与原来的“L”形组成的新图形既是轴对称图形又是中心对称图形;
(2)在图2中再涂黑2格,使新涂黑的图形与原来的“L”形组成的新图形是轴对称图形但不是中心对称图形.
七、综合题
25.某商场销售一批衬衫,平均每天可销售出20件,每件盈利50元,为扩大销售盈利,商场决定采取适当的降价措施,但要求每件盈利不少于30元,经调查发现,若每件衬衫每降价5元、则商场每天可多销售10件、若商场平均每天盈利1600元,则每件衬衫应降价多少元?
26.某百货商店服装在销售过程中发现,某品牌童装平均每天可售出20件,每件盈利40元,经市场调查发现,在进货不变的情况下,若每件童装每降价1元,日销售量将增加2件,当每件童装降价多少元时,这种童装一天的销售利润最多?最多利润是多少?
27.2019年在武汉市举行了军运会,在军运会比赛中,某次羽毛球的运动路线可以看作是抛物线(如图),其中出球点B离地面的距离是米,球落点的水平距离是多少?
八、实践探究题
28.在“综合与实践”活动中,某校九年级数学小组采用无人机辅助的方法测量一座桥的长度.如图,桥是水平并且笔直的,测量过程中,小组成员遥控无人机飞到桥的上方90m的点C处悬停,此时测得桥两端A,B两点的俯角分别为60°和45°,求桥的长度.(结果精确到1m.参考数据:,)
答案解析部分
1.【答案】
【知识点】二次函数图象的几何变换
2.【答案】1
【知识点】二次函数的定义
3.【答案】5
【知识点】二次函数的实际应用-喷水问题
4.【答案】
【知识点】含30°角的直角三角形;直线与圆的位置关系
5.【答案】,
【知识点】直接开平方法解一元二次方程
6.【答案】
【知识点】比例的性质
7.【答案】D
【知识点】角平分线的性质;线段垂直平分线的性质;相似三角形的判定与性质
8.【答案】D
【知识点】圆周角定理
9.【答案】B
【知识点】中心投影
10.【答案】C
【知识点】圆周角定理
11.【答案】C
【知识点】一元二次方程的应用-数字问题
12.【答案】(1),
(2),
【知识点】直接开平方法解一元二次方程;因式分解法解一元二次方程
【答案】13.正确
14.错误
15.正确
16.错误
【知识点】可能性的大小
17.【答案】
【知识点】可能性的大小;概率的意义
18.【答案】×
【知识点】可能性的大小
19.【答案】正确
【知识点】中心对称及中心对称图形
20.【答案】√
【知识点】可能性的大小
21.【答案】解:
,
[(x-1)-5][(x-1)+3]=0,
(x-1)-5=0或(x-1)+3=0,
所以x1=6,x2=-2.
【知识点】因式分解法解一元二次方程
22.【答案】(1)27.4秒;(2)0.7m;(3)7.6秒
【知识点】切线的性质;求特殊角的三角函数值;解直角三角形
23.【答案】(1)
(2)
(3)2
(4)或
【知识点】待定系数法求二次函数解析式;二次函数图象与坐标轴的交点问题
24.【答案】(1)如图1,作图不唯一,符合要求即可.
(2)如图2,作图不唯一,符合要求即可.
【知识点】轴对称图形;中心对称及中心对称图形
25.【答案】每件衬衫应降价10元
【知识点】一元二次方程的实际应用-销售问题
26.【答案】每件童装降价15元时,每天销售这种童装的利润最高,最高利润是1250元.
【知识点】二次函数的实际应用-销售问题
27.【答案】5米
【知识点】二次函数的实际应用-抛球问题
28.【答案】桥的长度约为.
【知识点】解直角三角形的实际应用﹣仰角俯角问题
21世纪教育网(www.21cnjy.com)
2 / 8
同课章节目录
