人教版数学九年级上册·下册综合检测题二(含答案)
文档属性
| 名称 | 人教版数学九年级上册·下册综合检测题二(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 772.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-27 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版数学九年级上册。下册综合检测题二(精华)
一、填空题
1.把抛物线向上平移个单位后得到的抛物线解析式是: .
2.若是关于的二次函数,则m的值为 .
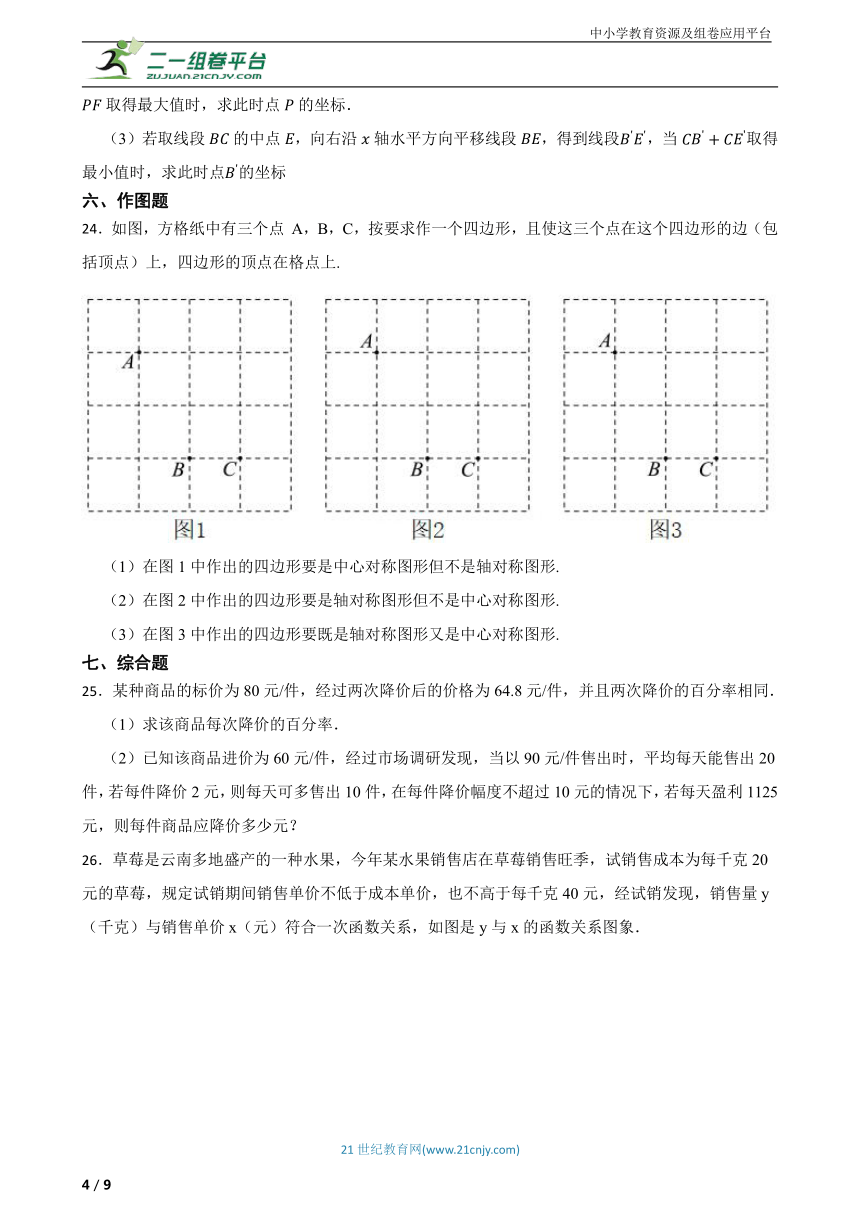
3.如图,当一喷灌架为一农田喷水时,喷灌架喷射出的水流可以近似地看成抛物线,则该喷灌架喷出的水可到达的最远距离 米.
4.如图①是某市地铁入口的双闸门,如图②,当它的双翼展开时,双翼边缘的端点 A 与B 之间的距离为,双翼的边缘,且与闸机侧立面夹角.,求当双翼收起时,两机箱之间的宽度为 .
5.方程(x-5)2=0的根是 .
6.若,则 .
二、单选题
7.如图,在△ABC中,∠C=90°,∠B=30°,边AB的垂直平分线DE交AB于点E,交BC于点D.CD=3,则BC的长为( )
A.6 B.9 C.6 D.3
8.如图所示,点在圆上,若,则的度数是( )
A. B. C. D.
9.晚上,小华出去散步,在经过一盏路灯时,他发现自己的身影( )
A.变长 B.变短
C.先变长后变短 D.先变短后变长
10.正多边形的一部分如图所示,若,则该正多边形的边数为( )
A.8 B.9 C.10 D.12
11.若一个两位数比它的十位数字与个位数字和的平方少2,且个位数字比十位数字大1,则这个两位数是( )
A.23 B.34 C.23或34 D.或
三、解答题
12.解方程:
(1);
(2);
(3).
四、判断题
判断:下列事件中,哪些事件发生的可能性是相同的 相同的画“√”,不相同的画“×”.
13.掷一枚质地均匀的骰子,出现1点或5点朝上的可能性.( )
14.从装有5个红球、3个白球的袋中任取一球,取到红球或白球的可能性. ( )
15.从一副扑克牌中任取一张,取到小王或黑桃5的可能性.( )
16.掷两枚质地均匀的骰子,出现的点数和是“2”或“5”的可能性.( )
17.盒子中有3个红球和2个白球,球除颜色外完全相同,从中任意摸出一个球,摸红球的可能性大.
18.投掷3次硬币,有2次正面朝上,1次反面朝上,那么,投掷第4次硬币正面朝上的可能性是.
19.线段是中心对称图形,对称中心是它的中点。
20.袋子里有同样多的红球和黄球,摸10次,摸到黄球的次数有可能比红球多.
五、计算题
21.解方程:
(1);
(2).
22.如图,正六边形是半径为1的的内接六边形,连接并延长到点,过点,交的延长线于点.
(1)是___________(填“直角”“等腰”或“等边”)三角形;
(2)当___________时,直线与相切,此时通过计算比较线段和劣弧长度哪个更长;(参考数据:取3)
(3)已知是上的动点(点不与点A,重合).
①连接,,求的度数;
②已知,过点作的切线,当切线与直线交于点时,请直接写出长的最小值.
23.已知抛物线与轴相交于A、B两点(点A在点B右侧),与轴相交于点C,点,.
(1)求抛物线的顶点坐标;
(2)若点是第二象限内抛物线上一动点,过点作线段轴,交直线于点,当线段取得最大值时,求此时点的坐标.
(3)若取线段的中点,向右沿轴水平方向平移线段,得到线段,当取得最小值时,求此时点的坐标
六、作图题
24.如图,方格纸中有三个点 A,B,C,按要求作一个四边形,且使这三个点在这个四边形的边(包括顶点)上,四边形的顶点在格点上.
(1)在图1中作出的四边形要是中心对称图形但不是轴对称图形.
(2)在图2中作出的四边形要是轴对称图形但不是中心对称图形.
(3)在图3中作出的四边形要既是轴对称图形又是中心对称图形.
七、综合题
25.某种商品的标价为80元/件,经过两次降价后的价格为64.8元/件,并且两次降价的百分率相同.
(1)求该商品每次降价的百分率.
(2)已知该商品进价为60元/件,经过市场调研发现,当以90元/件售出时,平均每天能售出20件,若每件降价2元,则每天可多售出10件,在每件降价幅度不超过10元的情况下,若每天盈利1125元,则每件商品应降价多少元?
26.草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.
(1)求y与x的函数解析式;
(2)设该水果销售店试销草莓获得的利润为W元,求W的最大值.
27.如图,排球运动员站在点O处练习发球,将球从O点正上方的B处发出.球出手后的运动路径为抛物线,抛物线的最高点C到y轴的距离为6米,竖直高度比出手点B高出1米.已知米,排球场的边界点A到O点的水平距离米,球网高度米,且.
(1)当时,求排球运动路径的抛物线解析式;
(2)当时,排球能否越过球网?请说明理由;
(3)若该运动员调整起跳高度,使球在点A处落地,此时形成的抛物线记为L1,球落地后立即向右弹起,形成另一条与形状相同的抛物线,且此时排球运行的最大高度为1米,球场外有一个吉祥物玩偶MN高米.排球经过向右反弹后沿的路径运动,若在下落的过程中,正好砸中玩偶的头部点M,求玩偶所处的位置点N与点A的距离.
八、实践探究题
28.某数学“综合与实践”小组的同学把“测量沈阳中山广场雕塑最高点的高度”作为一项课题活动,他们制定了测量方案,并利用课余时间完成了实地测量.为了减小测量误差,该小组在测量仰角以及两点间的距离时,都分别测量了两次并取它们的平均值作为测量结果测量数据如下表:
课题 测量中山广场雕塑最高点的高度
实物图 如图
成员 组长:××× 组员:×××,×××,×××
测量工具 卷尺.测角仪…
测量示意图 说明:表示南山门最高点到地面的竖直距离,测角仪的高度,点C、F与点B在同一直线上,点C、F之间的距离可直接测得,且点A、B、C、D、E、F在同一平面内.
测量数据 测量项目 第一次 第二次 平均值
的度数 42.5° 41.95° 42°
的度数 53.7° 52.93° 53°
C、F之间的距离 34.68m 34.72m 34.7m
… …
请根据该小组的同学根据上表中的测量数据,求中山广场雕塑最高点的高度.(结果精确到0.1m,参考数据:,).
答案解析部分
1.【答案】
【知识点】二次函数图象的几何变换
2.【答案】
【知识点】二次函数的定义
3.【答案】11
【知识点】二次函数的实际应用-喷水问题
4.【答案】68
【知识点】含30°角的直角三角形
5.【答案】x1=x2=5
【知识点】直接开平方法解一元二次方程
6.【答案】
【知识点】比例的性质
7.【答案】B
【知识点】角平分线的性质;线段垂直平分线的性质;含30°角的直角三角形
8.【答案】C
【知识点】圆周角定理
9.【答案】D
【知识点】中心投影;解直角三角形—边角关系
10.【答案】B
【知识点】圆周角定理;圆内接正多边形
11.【答案】A
【知识点】一元二次方程的应用-数字问题
12.【答案】(1),
(2),
(3),
【知识点】直接开平方法解一元二次方程;因式分解法解一元二次方程
【答案】13.正确
14.错误
15.正确
16.错误
【知识点】可能性的大小
17.【答案】
【知识点】可能性的大小;概率的意义
18.【答案】×
【知识点】可能性的大小
19.【答案】正确
【知识点】中心对称及中心对称图形
20.【答案】√
【知识点】可能性的大小
21.【答案】(1)
(2)
【知识点】直接开平方法解一元二次方程;因式分解法解一元二次方程
22.【答案】(1)等边
(2)
(3)①或,②
【知识点】圆周角定理;切线的性质;圆内接正多边形;解直角三角形
23.【答案】(1)
(2)
(3)
【知识点】待定系数法求二次函数解析式;平行四边形的判定与性质
24.【答案】(1)解:如图所示的四边形就是所求的图形;
(2)解:如图所示的四边形就是所求的图形;
(3)解:如图所示的四边形就是所求的图形;
【知识点】轴对称图形;中心对称及中心对称图形
25.【答案】(1)该商品每次降价的百分率为
(2)每件商品应降价5元.
【知识点】一元二次方程的实际应用-百分率问题;一元二次方程的实际应用-销售问题
26.【答案】(1)
(2)当时,W最大,最大值为5200元.
【知识点】待定系数法求一次函数解析式;二次函数的实际应用-销售问题
27.【答案】(1)抛物线的表达式为
(2)球能越过球网
(3)玩偶所处的位置点N与点A的距离为6米
【知识点】待定系数法求二次函数解析式;二次函数的实际应用-抛球问题
28.【答案】缝山针雕塑最高点的高度AB约为
【知识点】解直角三角形的实际应用﹣仰角俯角问题
21世纪教育网(www.21cnjy.com)
1 / 9
人教版数学九年级上册。下册综合检测题二(精华)
一、填空题
1.把抛物线向上平移个单位后得到的抛物线解析式是: .
2.若是关于的二次函数,则m的值为 .
3.如图,当一喷灌架为一农田喷水时,喷灌架喷射出的水流可以近似地看成抛物线,则该喷灌架喷出的水可到达的最远距离 米.
4.如图①是某市地铁入口的双闸门,如图②,当它的双翼展开时,双翼边缘的端点 A 与B 之间的距离为,双翼的边缘,且与闸机侧立面夹角.,求当双翼收起时,两机箱之间的宽度为 .
5.方程(x-5)2=0的根是 .
6.若,则 .
二、单选题
7.如图,在△ABC中,∠C=90°,∠B=30°,边AB的垂直平分线DE交AB于点E,交BC于点D.CD=3,则BC的长为( )
A.6 B.9 C.6 D.3
8.如图所示,点在圆上,若,则的度数是( )
A. B. C. D.
9.晚上,小华出去散步,在经过一盏路灯时,他发现自己的身影( )
A.变长 B.变短
C.先变长后变短 D.先变短后变长
10.正多边形的一部分如图所示,若,则该正多边形的边数为( )
A.8 B.9 C.10 D.12
11.若一个两位数比它的十位数字与个位数字和的平方少2,且个位数字比十位数字大1,则这个两位数是( )
A.23 B.34 C.23或34 D.或
三、解答题
12.解方程:
(1);
(2);
(3).
四、判断题
判断:下列事件中,哪些事件发生的可能性是相同的 相同的画“√”,不相同的画“×”.
13.掷一枚质地均匀的骰子,出现1点或5点朝上的可能性.( )
14.从装有5个红球、3个白球的袋中任取一球,取到红球或白球的可能性. ( )
15.从一副扑克牌中任取一张,取到小王或黑桃5的可能性.( )
16.掷两枚质地均匀的骰子,出现的点数和是“2”或“5”的可能性.( )
17.盒子中有3个红球和2个白球,球除颜色外完全相同,从中任意摸出一个球,摸红球的可能性大.
18.投掷3次硬币,有2次正面朝上,1次反面朝上,那么,投掷第4次硬币正面朝上的可能性是.
19.线段是中心对称图形,对称中心是它的中点。
20.袋子里有同样多的红球和黄球,摸10次,摸到黄球的次数有可能比红球多.
五、计算题
21.解方程:
(1);
(2).
22.如图,正六边形是半径为1的的内接六边形,连接并延长到点,过点,交的延长线于点.
(1)是___________(填“直角”“等腰”或“等边”)三角形;
(2)当___________时,直线与相切,此时通过计算比较线段和劣弧长度哪个更长;(参考数据:取3)
(3)已知是上的动点(点不与点A,重合).
①连接,,求的度数;
②已知,过点作的切线,当切线与直线交于点时,请直接写出长的最小值.
23.已知抛物线与轴相交于A、B两点(点A在点B右侧),与轴相交于点C,点,.
(1)求抛物线的顶点坐标;
(2)若点是第二象限内抛物线上一动点,过点作线段轴,交直线于点,当线段取得最大值时,求此时点的坐标.
(3)若取线段的中点,向右沿轴水平方向平移线段,得到线段,当取得最小值时,求此时点的坐标
六、作图题
24.如图,方格纸中有三个点 A,B,C,按要求作一个四边形,且使这三个点在这个四边形的边(包括顶点)上,四边形的顶点在格点上.
(1)在图1中作出的四边形要是中心对称图形但不是轴对称图形.
(2)在图2中作出的四边形要是轴对称图形但不是中心对称图形.
(3)在图3中作出的四边形要既是轴对称图形又是中心对称图形.
七、综合题
25.某种商品的标价为80元/件,经过两次降价后的价格为64.8元/件,并且两次降价的百分率相同.
(1)求该商品每次降价的百分率.
(2)已知该商品进价为60元/件,经过市场调研发现,当以90元/件售出时,平均每天能售出20件,若每件降价2元,则每天可多售出10件,在每件降价幅度不超过10元的情况下,若每天盈利1125元,则每件商品应降价多少元?
26.草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.
(1)求y与x的函数解析式;
(2)设该水果销售店试销草莓获得的利润为W元,求W的最大值.
27.如图,排球运动员站在点O处练习发球,将球从O点正上方的B处发出.球出手后的运动路径为抛物线,抛物线的最高点C到y轴的距离为6米,竖直高度比出手点B高出1米.已知米,排球场的边界点A到O点的水平距离米,球网高度米,且.
(1)当时,求排球运动路径的抛物线解析式;
(2)当时,排球能否越过球网?请说明理由;
(3)若该运动员调整起跳高度,使球在点A处落地,此时形成的抛物线记为L1,球落地后立即向右弹起,形成另一条与形状相同的抛物线,且此时排球运行的最大高度为1米,球场外有一个吉祥物玩偶MN高米.排球经过向右反弹后沿的路径运动,若在下落的过程中,正好砸中玩偶的头部点M,求玩偶所处的位置点N与点A的距离.
八、实践探究题
28.某数学“综合与实践”小组的同学把“测量沈阳中山广场雕塑最高点的高度”作为一项课题活动,他们制定了测量方案,并利用课余时间完成了实地测量.为了减小测量误差,该小组在测量仰角以及两点间的距离时,都分别测量了两次并取它们的平均值作为测量结果测量数据如下表:
课题 测量中山广场雕塑最高点的高度
实物图 如图
成员 组长:××× 组员:×××,×××,×××
测量工具 卷尺.测角仪…
测量示意图 说明:表示南山门最高点到地面的竖直距离,测角仪的高度,点C、F与点B在同一直线上,点C、F之间的距离可直接测得,且点A、B、C、D、E、F在同一平面内.
测量数据 测量项目 第一次 第二次 平均值
的度数 42.5° 41.95° 42°
的度数 53.7° 52.93° 53°
C、F之间的距离 34.68m 34.72m 34.7m
… …
请根据该小组的同学根据上表中的测量数据,求中山广场雕塑最高点的高度.(结果精确到0.1m,参考数据:,).
答案解析部分
1.【答案】
【知识点】二次函数图象的几何变换
2.【答案】
【知识点】二次函数的定义
3.【答案】11
【知识点】二次函数的实际应用-喷水问题
4.【答案】68
【知识点】含30°角的直角三角形
5.【答案】x1=x2=5
【知识点】直接开平方法解一元二次方程
6.【答案】
【知识点】比例的性质
7.【答案】B
【知识点】角平分线的性质;线段垂直平分线的性质;含30°角的直角三角形
8.【答案】C
【知识点】圆周角定理
9.【答案】D
【知识点】中心投影;解直角三角形—边角关系
10.【答案】B
【知识点】圆周角定理;圆内接正多边形
11.【答案】A
【知识点】一元二次方程的应用-数字问题
12.【答案】(1),
(2),
(3),
【知识点】直接开平方法解一元二次方程;因式分解法解一元二次方程
【答案】13.正确
14.错误
15.正确
16.错误
【知识点】可能性的大小
17.【答案】
【知识点】可能性的大小;概率的意义
18.【答案】×
【知识点】可能性的大小
19.【答案】正确
【知识点】中心对称及中心对称图形
20.【答案】√
【知识点】可能性的大小
21.【答案】(1)
(2)
【知识点】直接开平方法解一元二次方程;因式分解法解一元二次方程
22.【答案】(1)等边
(2)
(3)①或,②
【知识点】圆周角定理;切线的性质;圆内接正多边形;解直角三角形
23.【答案】(1)
(2)
(3)
【知识点】待定系数法求二次函数解析式;平行四边形的判定与性质
24.【答案】(1)解:如图所示的四边形就是所求的图形;
(2)解:如图所示的四边形就是所求的图形;
(3)解:如图所示的四边形就是所求的图形;
【知识点】轴对称图形;中心对称及中心对称图形
25.【答案】(1)该商品每次降价的百分率为
(2)每件商品应降价5元.
【知识点】一元二次方程的实际应用-百分率问题;一元二次方程的实际应用-销售问题
26.【答案】(1)
(2)当时,W最大,最大值为5200元.
【知识点】待定系数法求一次函数解析式;二次函数的实际应用-销售问题
27.【答案】(1)抛物线的表达式为
(2)球能越过球网
(3)玩偶所处的位置点N与点A的距离为6米
【知识点】待定系数法求二次函数解析式;二次函数的实际应用-抛球问题
28.【答案】缝山针雕塑最高点的高度AB约为
【知识点】解直角三角形的实际应用﹣仰角俯角问题
21世纪教育网(www.21cnjy.com)
1 / 9
同课章节目录
