第十四章整式的乘法与因式分解 章末综合试题 2024--2025学年上学期初中数学人教版八年级上册
文档属性
| 名称 | 第十四章整式的乘法与因式分解 章末综合试题 2024--2025学年上学期初中数学人教版八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 463.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-26 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第十四章整式的乘法与因式分解 章末综合试题 2024--2025学年上学期初中数学人教版八年级上册
一、单选题
1.下列运算正确的是( )
A. B.
C. D.
2.计算: = ( )
A. B. C. D.
3.比较与大小,结果是( )
A.前者大 B.一样大 C.后者大 D.无法确定
4.若,,则等于( )
A. B. C. D.
5.已知单项式与的积为,则,的值为( )
A., B.,
C., D.,
6.若等式对任意实数都成立,那么, 的值分别是( )
A. B. C. D.
7.已知,则的值为( )
A. B.
C. D.
8.下列多项式中,既能用提取公因式又能用平方差公式进行因式分解的是( ).
A. B. C. D.
9.如图,两个正方形的边长分别为a和b,如果,,那么阴影部分的面积是( )
A.15 B.17 C.20 D.22
10.阅读下列两个多项式相乘的运算过程,解决下面的问题:
四个学生一起做乘法,其中a是正数,那么最后得出的结果是( )
A. B.
C. D.
二、填空题
11.计算的结果等于 .
12.计算: .
13.计算: .
14.因式分解: .
15.已知,,则 .
16.已知代数式是一个完全平方式,则实数t的值为 .
17.已知,则 .
18.已知a+b=1,则代数式a2﹣b2 +2b+9的值为 .
三、解答题
19.把下列各式分解因式:
(1);
(2).
20.已知,,,求的值.
21.先化简,再求值:,其中,.
22.先化简,再求值:,其中.
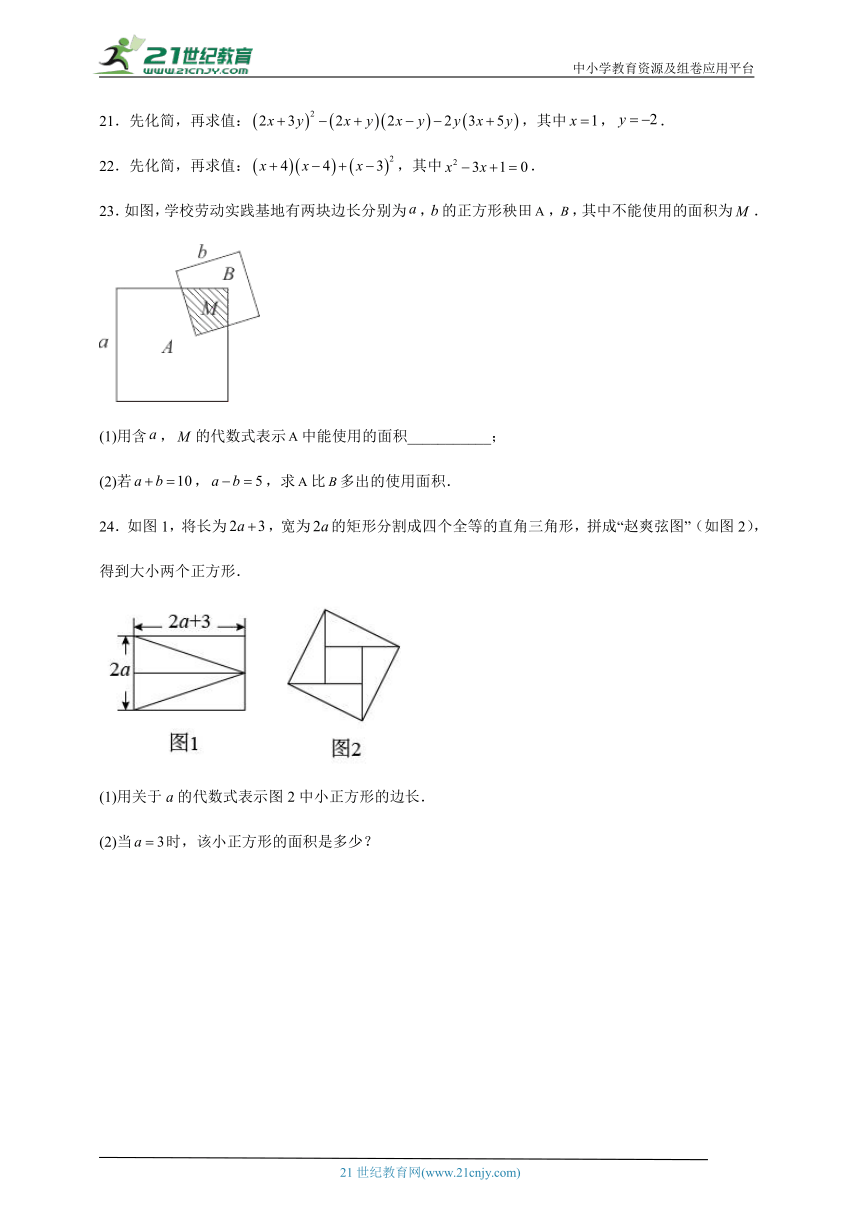
23.如图,学校劳动实践基地有两块边长分别为,的正方形秧田,,其中不能使用的面积为.
(1)用含,的代数式表示中能使用的面积___________;
(2)若,,求比多出的使用面积.
24.如图1,将长为,宽为的矩形分割成四个全等的直角三角形,拼成“赵爽弦图”(如图2),得到大小两个正方形.
(1)用关于a的代数式表示图2中小正方形的边长.
(2)当时,该小正方形的面积是多少?
参考答案:
1.A
本题考查的是同底数幂的乘法,幂的乘方,积的乘方和合并同类项的法则,根据同底数幂的乘法,幂的乘方,积的乘方和合并同类项的法则对各选项进行解答即可.
解:A、,正确,符合题意;
B、,原计算错误,不符合题意;
C、,原计算错误,不符合题意;
D、和不是同类项,不能合并;
2.A
本题考查单项式乘以单项式,积的乘方,掌握相关的运算法则是解题的关键.先算积的乘方,再算单项式乘以单项式,求解即可.
原式
3.A
本题考查了幂的乘方与积的乘方及同底数幂的乘法,有理数大小比较,先把与变为,再比较底数,即可得出答案.
解:,
,
,
4.A
本题考查了幂的乘方与积的乘方以及二元一次方程,解题的关键是掌握以上运算法则.
先把化为,化为,然后根据,,列出方程式,再解方程即可求解.
解:,
,
,
解得:,
,
,
5.A
此题考查了单项式的乘法运算,按照单项式乘单项式计算单项与的积,再根据单项式与的积为,即可求得答案.
解:∵,单项式与的积为,
∴,,
6.B
本题主要考查了多项式乘以多项式,解一元一次方程,先按照多项式乘以多项式计算,然后根据已知条件得出,,解一元一次方程即可求出m,n的值.
解: ,
∵ ,等式对任意实数都成立,
∴,,
解得:,,
7.A
本题主要考查的是多项式的因式分解,掌握其运算法则是解决此题关键.首先根据多项式乘多项式的运算法则计算已知等式的右边,再根据系数相等可得答案.
解:∵,
∴,
∴,,
,,故A正确.
8.C
根据提取公因式和平方差公式“”因式分解,逐项判定即可.
解:A、,不能因式分解,故该选项不符合题意;
B、,只用了提取公因式来因式分解,故该选项不符合题意;
C、,用了提取公因式和平方差公式进行因式分解,故该选项符合题意;
D、 ,只用了提取公因式来因式分解,故该选项不符合题意.
9.B
此题考查了完全平方公式的几何意义,适当的变形是解决问题的关键.用含a,b的代数式表示出阴影部分面积,再整体代入求值即可.
解:由题意可得:阴影部分面积
;
∵,,
∴,
∴阴影部分面积.
10.A
本题考查了整式的混合运算化简求值.根据题意可得:,再根据,从而可得,进而可得:,然后求出:,从而可得,即可解答.
解:由题意得:,
,
,
由题意得:,
解得:,
,
,
11.
根据同底数幂的乘法即可求得答案.
解:,
故答案为:.
12.
根据“幂的乘方,底数不变,指数相乘法则”处理.
解:,
故答案为:
13./
本题考查了整式的运算.利用单项式乘单项式法则计算即可.
解:.
故答案为:.
14.
将看做一个整体,则9等于3得的平方,逆用完全平方公式因式分解即可.
解:
,
故答案为:.
15.24
根据平方差公式计算即可.
解:∵,,
∴,
故答案为:24.
16.或
直接利用完全平方公式求解.
解:∵代数式是一个完全平方式,
∴,
∴,
解得或,
故答案为:或
17.
根据已知式子,凑完全平方公式,根据非负数之和为0,分别求得的值,进而代入代数式即可求解.
解:,
,
即,
,
,
故答案为:.
18.10
根据平方差公式,把原式化为,可得,即可求解.
解:a2﹣b2 +2b+9
故答案为:10
19.(1)
(2)
(1)两次运用平方差公式分解即可;
(2)根据完全平方公式和平方差公式解答即可.
(1)
.
(2)
.
20.
根据幂的乘方,同底数幂的乘法和除法进行计算即可.
解:∵,,,
∴
.
21.,
先根据完全平方、平方差公式和单项式乘以多项式的法则计算展开,再代值计算.
解:原式
.
当,时,
原式.
22.,-9
根据平方差公式和完全平方公式可以化简题目中的式子,然后将x的值代入化简后的式子即可解答本题.
解:原式
.
,
,
原式
23.(1)
(2)50
(1)利用正方形秧田的面积减去不能使用的面积即可得;
(2)先求出中能使用的面积为,再求出比多出的使用面积为,利用平方差公式求解即可得.
(1)解:中能使用的面积为,
故答案为:.
(2)解:中能使用的面积为,
则比多出的使用面积为,
,,
,
答:比多出的使用面积为50.
24.(1)
(2)36
(1)分别算出直角三角形较长的直角边和较短的直角边,再用较长的直角边减去较短的直角边即可得到小正方形面积;
(2)根据(1)所得的小正方形边长,可以写出小正方形的面积代数式,再将a的值代入即可.
(1)解:∵直角三角形较短的直角边,
较长的直角边,
∴小正方形的边长;
(2)解:,
当时,.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第十四章整式的乘法与因式分解 章末综合试题 2024--2025学年上学期初中数学人教版八年级上册
一、单选题
1.下列运算正确的是( )
A. B.
C. D.
2.计算: = ( )
A. B. C. D.
3.比较与大小,结果是( )
A.前者大 B.一样大 C.后者大 D.无法确定
4.若,,则等于( )
A. B. C. D.
5.已知单项式与的积为,则,的值为( )
A., B.,
C., D.,
6.若等式对任意实数都成立,那么, 的值分别是( )
A. B. C. D.
7.已知,则的值为( )
A. B.
C. D.
8.下列多项式中,既能用提取公因式又能用平方差公式进行因式分解的是( ).
A. B. C. D.
9.如图,两个正方形的边长分别为a和b,如果,,那么阴影部分的面积是( )
A.15 B.17 C.20 D.22
10.阅读下列两个多项式相乘的运算过程,解决下面的问题:
四个学生一起做乘法,其中a是正数,那么最后得出的结果是( )
A. B.
C. D.
二、填空题
11.计算的结果等于 .
12.计算: .
13.计算: .
14.因式分解: .
15.已知,,则 .
16.已知代数式是一个完全平方式,则实数t的值为 .
17.已知,则 .
18.已知a+b=1,则代数式a2﹣b2 +2b+9的值为 .
三、解答题
19.把下列各式分解因式:
(1);
(2).
20.已知,,,求的值.
21.先化简,再求值:,其中,.
22.先化简,再求值:,其中.
23.如图,学校劳动实践基地有两块边长分别为,的正方形秧田,,其中不能使用的面积为.
(1)用含,的代数式表示中能使用的面积___________;
(2)若,,求比多出的使用面积.
24.如图1,将长为,宽为的矩形分割成四个全等的直角三角形,拼成“赵爽弦图”(如图2),得到大小两个正方形.
(1)用关于a的代数式表示图2中小正方形的边长.
(2)当时,该小正方形的面积是多少?
参考答案:
1.A
本题考查的是同底数幂的乘法,幂的乘方,积的乘方和合并同类项的法则,根据同底数幂的乘法,幂的乘方,积的乘方和合并同类项的法则对各选项进行解答即可.
解:A、,正确,符合题意;
B、,原计算错误,不符合题意;
C、,原计算错误,不符合题意;
D、和不是同类项,不能合并;
2.A
本题考查单项式乘以单项式,积的乘方,掌握相关的运算法则是解题的关键.先算积的乘方,再算单项式乘以单项式,求解即可.
原式
3.A
本题考查了幂的乘方与积的乘方及同底数幂的乘法,有理数大小比较,先把与变为,再比较底数,即可得出答案.
解:,
,
,
4.A
本题考查了幂的乘方与积的乘方以及二元一次方程,解题的关键是掌握以上运算法则.
先把化为,化为,然后根据,,列出方程式,再解方程即可求解.
解:,
,
,
解得:,
,
,
5.A
此题考查了单项式的乘法运算,按照单项式乘单项式计算单项与的积,再根据单项式与的积为,即可求得答案.
解:∵,单项式与的积为,
∴,,
6.B
本题主要考查了多项式乘以多项式,解一元一次方程,先按照多项式乘以多项式计算,然后根据已知条件得出,,解一元一次方程即可求出m,n的值.
解: ,
∵ ,等式对任意实数都成立,
∴,,
解得:,,
7.A
本题主要考查的是多项式的因式分解,掌握其运算法则是解决此题关键.首先根据多项式乘多项式的运算法则计算已知等式的右边,再根据系数相等可得答案.
解:∵,
∴,
∴,,
,,故A正确.
8.C
根据提取公因式和平方差公式“”因式分解,逐项判定即可.
解:A、,不能因式分解,故该选项不符合题意;
B、,只用了提取公因式来因式分解,故该选项不符合题意;
C、,用了提取公因式和平方差公式进行因式分解,故该选项符合题意;
D、 ,只用了提取公因式来因式分解,故该选项不符合题意.
9.B
此题考查了完全平方公式的几何意义,适当的变形是解决问题的关键.用含a,b的代数式表示出阴影部分面积,再整体代入求值即可.
解:由题意可得:阴影部分面积
;
∵,,
∴,
∴阴影部分面积.
10.A
本题考查了整式的混合运算化简求值.根据题意可得:,再根据,从而可得,进而可得:,然后求出:,从而可得,即可解答.
解:由题意得:,
,
,
由题意得:,
解得:,
,
,
11.
根据同底数幂的乘法即可求得答案.
解:,
故答案为:.
12.
根据“幂的乘方,底数不变,指数相乘法则”处理.
解:,
故答案为:
13./
本题考查了整式的运算.利用单项式乘单项式法则计算即可.
解:.
故答案为:.
14.
将看做一个整体,则9等于3得的平方,逆用完全平方公式因式分解即可.
解:
,
故答案为:.
15.24
根据平方差公式计算即可.
解:∵,,
∴,
故答案为:24.
16.或
直接利用完全平方公式求解.
解:∵代数式是一个完全平方式,
∴,
∴,
解得或,
故答案为:或
17.
根据已知式子,凑完全平方公式,根据非负数之和为0,分别求得的值,进而代入代数式即可求解.
解:,
,
即,
,
,
故答案为:.
18.10
根据平方差公式,把原式化为,可得,即可求解.
解:a2﹣b2 +2b+9
故答案为:10
19.(1)
(2)
(1)两次运用平方差公式分解即可;
(2)根据完全平方公式和平方差公式解答即可.
(1)
.
(2)
.
20.
根据幂的乘方,同底数幂的乘法和除法进行计算即可.
解:∵,,,
∴
.
21.,
先根据完全平方、平方差公式和单项式乘以多项式的法则计算展开,再代值计算.
解:原式
.
当,时,
原式.
22.,-9
根据平方差公式和完全平方公式可以化简题目中的式子,然后将x的值代入化简后的式子即可解答本题.
解:原式
.
,
,
原式
23.(1)
(2)50
(1)利用正方形秧田的面积减去不能使用的面积即可得;
(2)先求出中能使用的面积为,再求出比多出的使用面积为,利用平方差公式求解即可得.
(1)解:中能使用的面积为,
故答案为:.
(2)解:中能使用的面积为,
则比多出的使用面积为,
,,
,
答:比多出的使用面积为50.
24.(1)
(2)36
(1)分别算出直角三角形较长的直角边和较短的直角边,再用较长的直角边减去较短的直角边即可得到小正方形面积;
(2)根据(1)所得的小正方形边长,可以写出小正方形的面积代数式,再将a的值代入即可.
(1)解:∵直角三角形较短的直角边,
较长的直角边,
∴小正方形的边长;
(2)解:,
当时,.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
