20.3一次函数的应用同步练习
图片预览
文档简介
一次函数的应用 同步练习
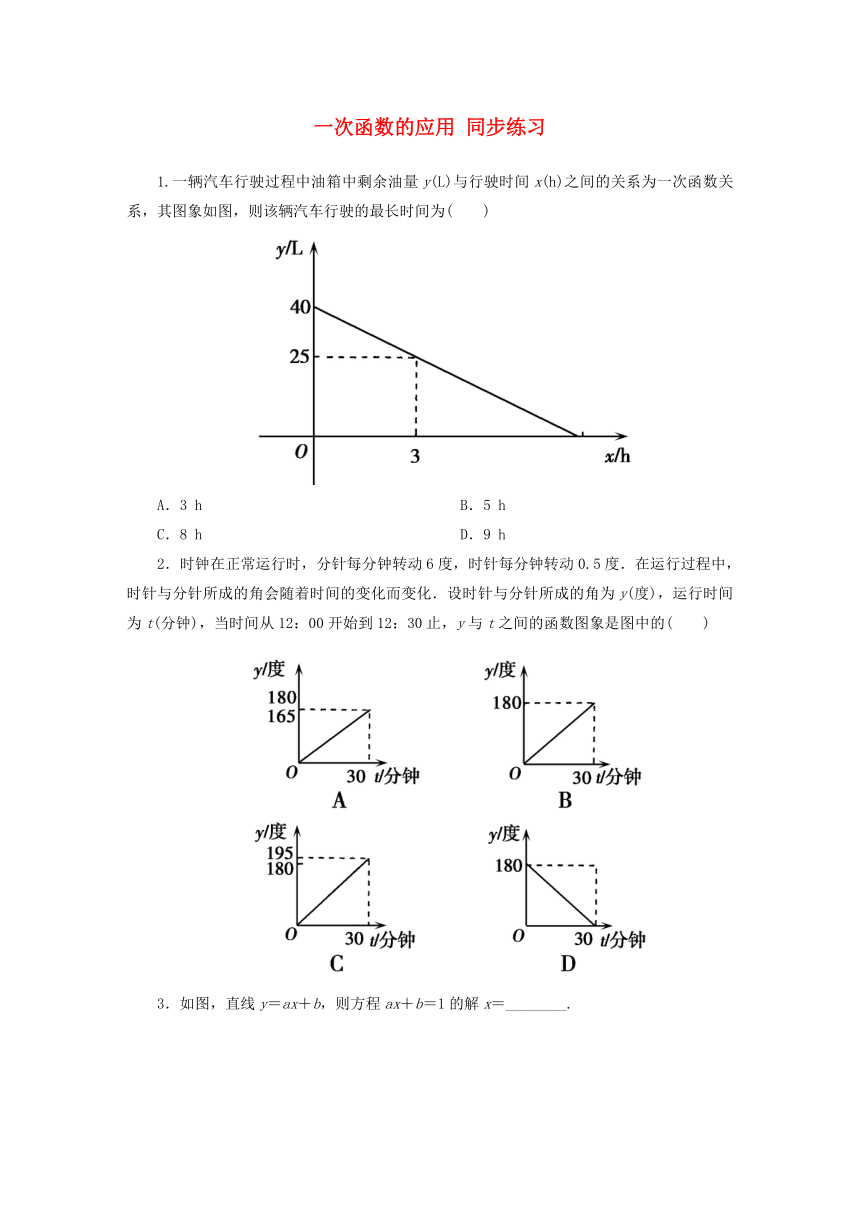
1.一辆汽车行驶过程中油箱中剩余油量y(L)与行驶时间x(h)之间的关系为一次函数关系,其图象如图,则该辆汽车行驶的最长时间为( )
( http: / / www.21cnjy.com )
A.3 h B.5 h
C.8 h D.9 h
2.时钟在正常运行时,分针每分钟转动6度 ( http: / / www.21cnjy.com ),时针每分钟转动0.5度.在运行过程中,时针与分针所成的角会随着时间的变化而变化.设时针与分针所成的角为y(度),运行时间为t(分钟),当时间从12:00开始到12:30止,y与t之间的函数图象是图中的( )
( http: / / www.21cnjy.com )
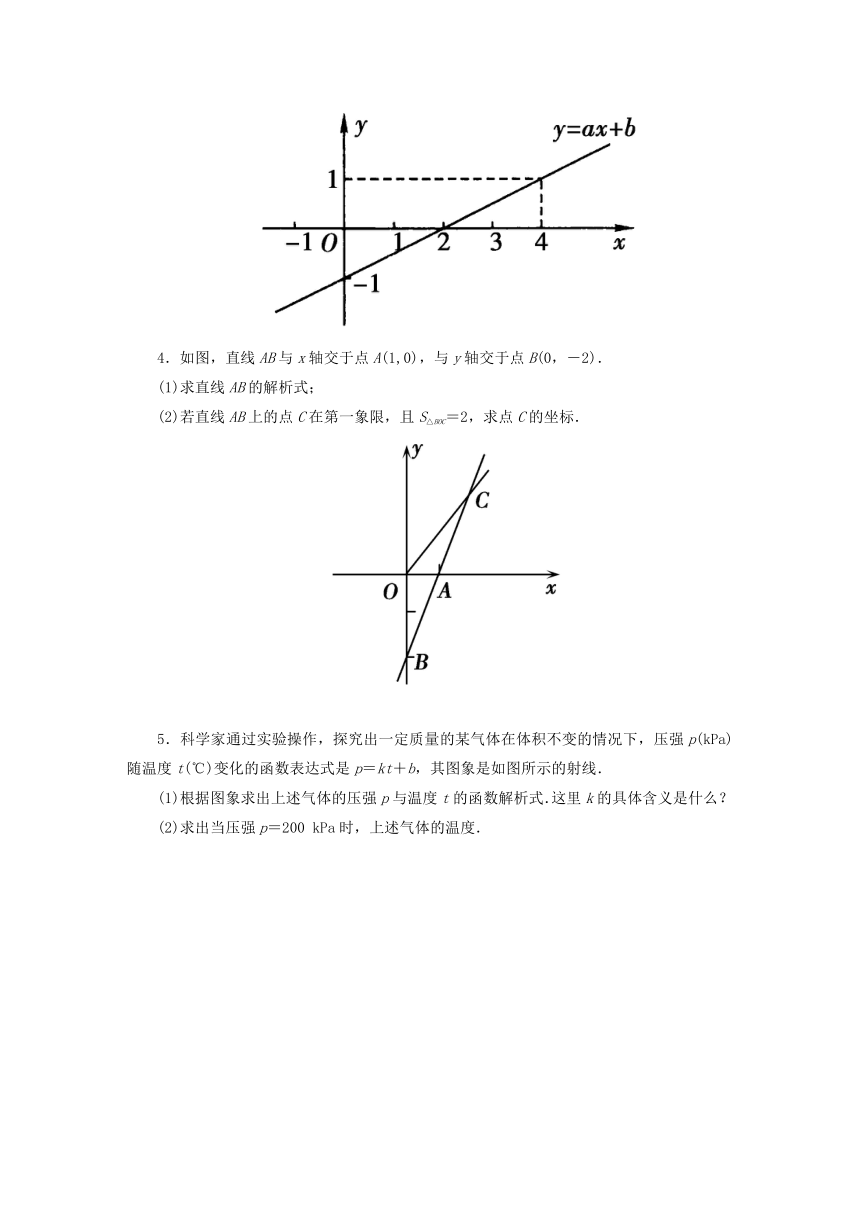
3.如图,直线y=ax+b,则方程ax+b=1的解x=________.
( http: / / www.21cnjy.com )
4.如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2).
(1)求直线AB的解析式;
(2)若直线AB上的点C在第一象限,且S△BOC=2,求点C的坐标.
( http: / / www.21cnjy.com )
5.科学家通过实验操作,探究出一定质量的某 ( http: / / www.21cnjy.com )气体在体积不变的情况下,压强p(kPa)随温度t(℃)变化的函数表达式是p=kt+b,其图象是如图所示的射线.
(1)根据图象求出上述气体的压强p与温度t的函数解析式.这里k的具体含义是什么?
(2)求出当压强p=200 kPa时,上述气体的温度.
( http: / / www.21cnjy.com )
6.某地区的电力资源丰富,并且得到了较好的 ( http: / / www.21cnjy.com )开发.该地区一家供电公司为了鼓励居民用电,采用分段计费的方法来计算电费.月用电量x(度)与相应的电费y(元)之间的函数图象如图所示.
(1)当月用电量为100度时,应交电费多少元?
(2)当x≥100时,求y与x之间的函数解析式?
(3)当月用电量为260度时,应交电费多少元?
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
7.(2013·黄冈)钓鱼 ( http: / / www.21cnjy.com )岛自古就是中国领土,中国政府已对钓鱼岛开展常态化巡逻.某天,为按计划准点到达指定海域,某巡逻艇凌晨1:00出发,匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,该艇加快速度仍匀速前进,结果恰好准点到达.如图是该艇行驶的路程y(海里)与所用时间t(小时)的函数图象,则该巡逻艇原计划准点到达的时刻是________.
课后作业
1.C 由图象可知汽车3小时耗油40-25=15 L,每小时耗油5升,40÷5=8 h.
2.A 函数关系式为y=6t-0.5t,即y=5.5t,当t=30时,y=165,故选A.
3.4 ∵把y=1代入y=ax+b得ax+b=1,∵(4,1)是直线y=ax+b上的点,∴x=4.
4.解:(1)设直线AB的解析式为y=kx+b.
把x=1,y=0;x=0,y=-2代入得:
k+b=0,b=-2,∴k=2,∴y=2x-2.
(2)∵B(0,-2),∴OB=2.
设C点坐标为(x,y)
∴S△BOC=OB·x=2,
×2·x=2,
x=2.
∵C点在直线AB上,∴把x=2代入y=2x-2得,y=2×2-2=2.
∴C点坐标为(2,2)
5.解:(1)把(0,100),(50 ( http: / / www.21cnjy.com ),120)代入p=kt+b,得100=b,120=50k+b,解得k=0.4,b=100,所以函数解析式为
p=0.4t+100(t≥0).k表示每升高1℃,压强增加0.4kPa.
(2)当p=200时,200=0.4t+100,所以t=250,此时气体的温度为250℃.
6.解:(1)由图象可知,当月用电量为100度时,应交电费60元.
(2)设y=kx+b,把x=100,y=60;x=200,y=110代入得
解得∴y=x+10(x≥100).
(3)把x=260代入y=x+10得,×260+10=140(元).
中考链接
7.7:00 本题考查一次函数图象 ( http: / / www.21cnjy.com )的应用,由图象反映的信息可知巡逻艇开始的速度为80海里/时,1小时后发生故障耽搁1小时,后将速度提高100海里/时,结果准时到达.根据这些已知条件可设原计划x小时到达,则可列方程80x=(x-2)×100+80,解得x=6.故原计划到达的时间为7:00.
1.一辆汽车行驶过程中油箱中剩余油量y(L)与行驶时间x(h)之间的关系为一次函数关系,其图象如图,则该辆汽车行驶的最长时间为( )
( http: / / www.21cnjy.com )
A.3 h B.5 h
C.8 h D.9 h
2.时钟在正常运行时,分针每分钟转动6度 ( http: / / www.21cnjy.com ),时针每分钟转动0.5度.在运行过程中,时针与分针所成的角会随着时间的变化而变化.设时针与分针所成的角为y(度),运行时间为t(分钟),当时间从12:00开始到12:30止,y与t之间的函数图象是图中的( )
( http: / / www.21cnjy.com )
3.如图,直线y=ax+b,则方程ax+b=1的解x=________.
( http: / / www.21cnjy.com )
4.如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2).
(1)求直线AB的解析式;
(2)若直线AB上的点C在第一象限,且S△BOC=2,求点C的坐标.
( http: / / www.21cnjy.com )
5.科学家通过实验操作,探究出一定质量的某 ( http: / / www.21cnjy.com )气体在体积不变的情况下,压强p(kPa)随温度t(℃)变化的函数表达式是p=kt+b,其图象是如图所示的射线.
(1)根据图象求出上述气体的压强p与温度t的函数解析式.这里k的具体含义是什么?
(2)求出当压强p=200 kPa时,上述气体的温度.
( http: / / www.21cnjy.com )
6.某地区的电力资源丰富,并且得到了较好的 ( http: / / www.21cnjy.com )开发.该地区一家供电公司为了鼓励居民用电,采用分段计费的方法来计算电费.月用电量x(度)与相应的电费y(元)之间的函数图象如图所示.
(1)当月用电量为100度时,应交电费多少元?
(2)当x≥100时,求y与x之间的函数解析式?
(3)当月用电量为260度时,应交电费多少元?
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
7.(2013·黄冈)钓鱼 ( http: / / www.21cnjy.com )岛自古就是中国领土,中国政府已对钓鱼岛开展常态化巡逻.某天,为按计划准点到达指定海域,某巡逻艇凌晨1:00出发,匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,该艇加快速度仍匀速前进,结果恰好准点到达.如图是该艇行驶的路程y(海里)与所用时间t(小时)的函数图象,则该巡逻艇原计划准点到达的时刻是________.
课后作业
1.C 由图象可知汽车3小时耗油40-25=15 L,每小时耗油5升,40÷5=8 h.
2.A 函数关系式为y=6t-0.5t,即y=5.5t,当t=30时,y=165,故选A.
3.4 ∵把y=1代入y=ax+b得ax+b=1,∵(4,1)是直线y=ax+b上的点,∴x=4.
4.解:(1)设直线AB的解析式为y=kx+b.
把x=1,y=0;x=0,y=-2代入得:
k+b=0,b=-2,∴k=2,∴y=2x-2.
(2)∵B(0,-2),∴OB=2.
设C点坐标为(x,y)
∴S△BOC=OB·x=2,
×2·x=2,
x=2.
∵C点在直线AB上,∴把x=2代入y=2x-2得,y=2×2-2=2.
∴C点坐标为(2,2)
5.解:(1)把(0,100),(50 ( http: / / www.21cnjy.com ),120)代入p=kt+b,得100=b,120=50k+b,解得k=0.4,b=100,所以函数解析式为
p=0.4t+100(t≥0).k表示每升高1℃,压强增加0.4kPa.
(2)当p=200时,200=0.4t+100,所以t=250,此时气体的温度为250℃.
6.解:(1)由图象可知,当月用电量为100度时,应交电费60元.
(2)设y=kx+b,把x=100,y=60;x=200,y=110代入得
解得∴y=x+10(x≥100).
(3)把x=260代入y=x+10得,×260+10=140(元).
中考链接
7.7:00 本题考查一次函数图象 ( http: / / www.21cnjy.com )的应用,由图象反映的信息可知巡逻艇开始的速度为80海里/时,1小时后发生故障耽搁1小时,后将速度提高100海里/时,结果准时到达.根据这些已知条件可设原计划x小时到达,则可列方程80x=(x-2)×100+80,解得x=6.故原计划到达的时间为7:00.
