2024-2025学年四川省成都市锦江区盐道街中学九年级(上)期中数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年四川省成都市锦江区盐道街中学九年级(上)期中数学试卷(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-26 00:00:00 | ||
图片预览


文档简介
2024-2025学年四川省成都市锦江区盐道街中学九年级(上)期中数学试卷
一、选择题(每小题4分。共32分)
1.(4分)如图所示,该几何体的俯视图是( )
A. B. C. D.
2.(4分)下列各组线段(单位:m)中,成比例线段的是( )
A.3,4,5,6 B.1,3,5,7
C.2,3,4,6 D.0.2,0.3,0.4,0.5
3.(4分)下列函数中,变量y是x的反比例函数的是( )
A. B. C. D.
4.(4分)如图,平行四边形ABCD对角线AC,BD交于点O,请添加一个条件:( ),使得平行四边形ABCD是矩形.
A.AB=BC B.AC⊥BD C.AB=DC D.AC=BD
5.(4分)甲、乙、丙、丁4名同学参加读书日志愿服务活动,甲同学是男生,乙、丙、丁同学都是女生,从这4名同学中随机抽取2名同学,则抽到的2名同学都是女生的概率为( )
A. B. C. D.
6.(4分)如图,在长为32米、宽为20米的矩形地面上修筑同样宽的道路(图中阴影部分),余下部分种植草坪,要使草坪的面积为540平方米,设道路的宽x米,则可列方程为( )
A.32×20﹣32x﹣20x=540
B.(32﹣x)(20﹣x)+x2=540
C.32x+20x=540
D.(32﹣x)(20﹣x)=540
7.(4分)已知(﹣5,y1)(﹣1,y2),(2,y3)都在双曲线y=(k>0)上,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y3<y1<y2 C.y2<y1<y3 D.y3<y2<y1
8.(4分)如图,在△ABC中,AD是BC边上中线,F是线段AD上一点,且AF:FD=2:3,连接CF并延长交AB于E,则AE:EB等于( )
A.1:2 B.2:3 C.1:3 D.3:5
二、填空题(每小题4分,共20分)
9.(4分)若2a=3b,则= .
10.(4分)已知关于x的方程(m﹣2)x|m|﹣3x﹣4=0是一元二次方程,则m= .
11.(4分)如图是初三某班学习小组设计用手电筒来测量逸夫楼高度的示意图.点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到逸夫楼CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=0.8m,BP=1.2m,PD=27m,那么逸夫楼的高度为 m.
12.(4分)如图,在△ADE中,BC∥DE,其中BC=2,DE=3,S△ABC=8,则S四边形BDEC= .
13.(4分)如图,BD是 ABCD的对角线,按以下步骤作图:①分别以点B和点D为圆心,
大于BD的长为半径作弧,两弧相交于E,F两点;②作直线EF,分别交AD,BC于点M,N,连接BM,DN.若BD=8,MN=6,则 ABCD的边BC上的高为 .
三、解答题(共48分)
14.(12分)(1)计算:;
(2)解方程:x2﹣4x+3=x;
(3)解方程:x2﹣4=5(x﹣2).
15.(8分)如图,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0),A(2,1),B(1,﹣2).
(1)画出将△OAB向左平移2个单位,再向上平移1个单位后得到的△O1A1B1;
(2)以原点O为位似中心,在y轴的右侧画出△OAB的一个位似△OA2B2,使它与△OAB的相似比为2:1;
(3)判断△O1A1B1和△OA2B2是否是位似图形(直接写结果),若是,请在图中标出位似中心点M,并写出点M的坐标.
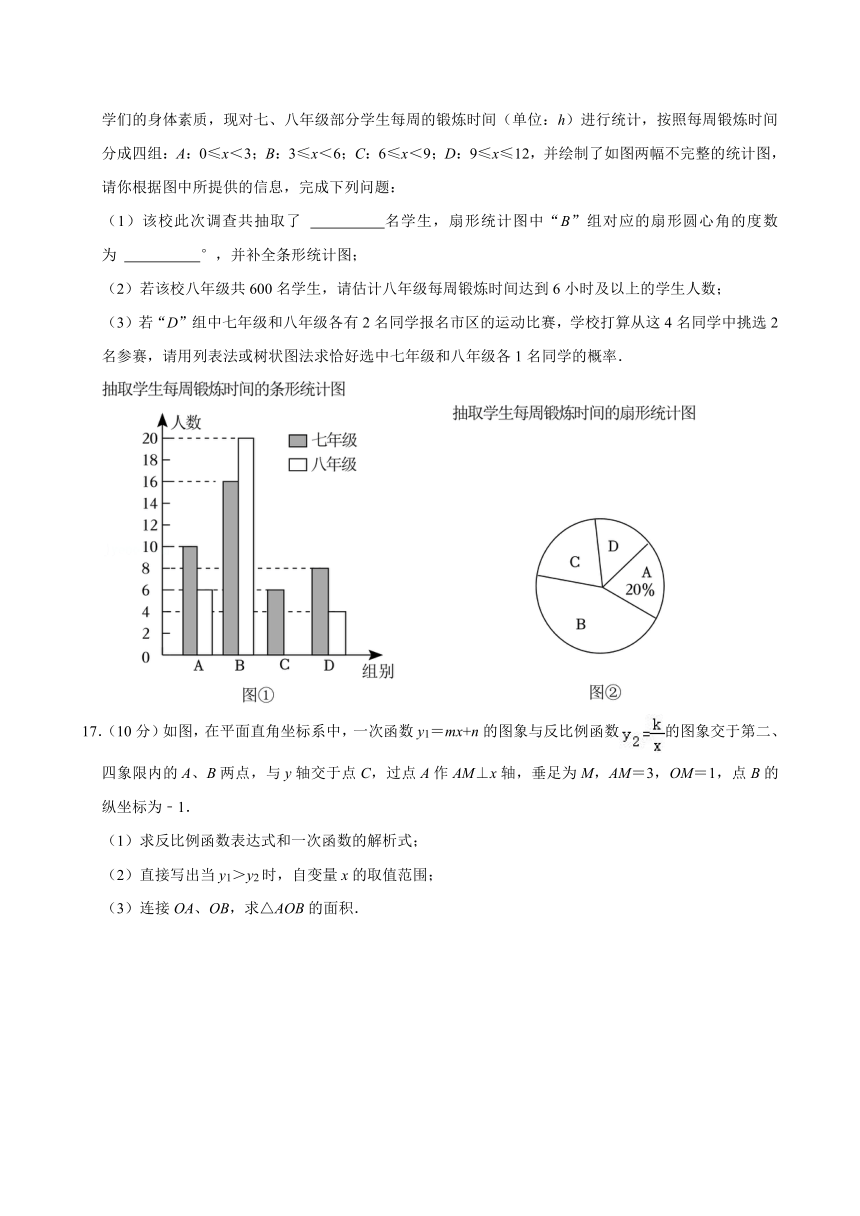
16.(8分)为了贯彻落实健康第一的指导思想,促进学生全面发展,我校积极倡导人文运动观念,提高同学们的身体素质,现对七、八年级部分学生每周的锻炼时间(单位:h)进行统计,按照每周锻炼时间分成四组:A:0≤x<3;B:3≤x<6;C:6≤x<9;D:9≤x≤12,并绘制了如图两幅不完整的统计图,请你根据图中所提供的信息,完成下列问题:
(1)该校此次调查共抽取了 名学生,扇形统计图中“B”组对应的扇形圆心角的度数为 °,并补全条形统计图;
(2)若该校八年级共600名学生,请估计八年级每周锻炼时间达到6小时及以上的学生人数;
(3)若“D”组中七年级和八年级各有2名同学报名市区的运动比赛,学校打算从这4名同学中挑选2名参赛,请用列表法或树状图法求恰好选中七年级和八年级各1名同学的概率.
17.(10分)如图,在平面直角坐标系中,一次函数y1=mx+n的图象与反比例函数的图象交于第二、四象限内的A、B两点,与y轴交于点C,过点A作AM⊥x轴,垂足为M,AM=3,OM=1,点B的纵坐标为﹣1.
(1)求反比例函数表达式和一次函数的解析式;
(2)直接写出当y1>y2时,自变量x的取值范围;
(3)连接OA、OB,求△AOB的面积.
18.(10分)在四边形ABCD中,AB∥CD,AB⊥BC且AB=BC.将AB绕点A顺时针旋转一定角度得线段AE,点E在四边形ABCD内部,连接DE,∠AED=90°,连接BE并延长交CD于点F.
(1)如图1,若AE=BE,过点A作CD延长线的垂线,垂足为G,求∠DAG的度数;
(2)如图2,若E为BF的中点,求的值;
(3)如图四:若,连接CE并延长交AD于点G,EG=3,求AB的长.
一、填空题(每小题4分,共20分)
19.(4分)已知m、n是x2﹣x﹣3=0的两个根,则的值为 .
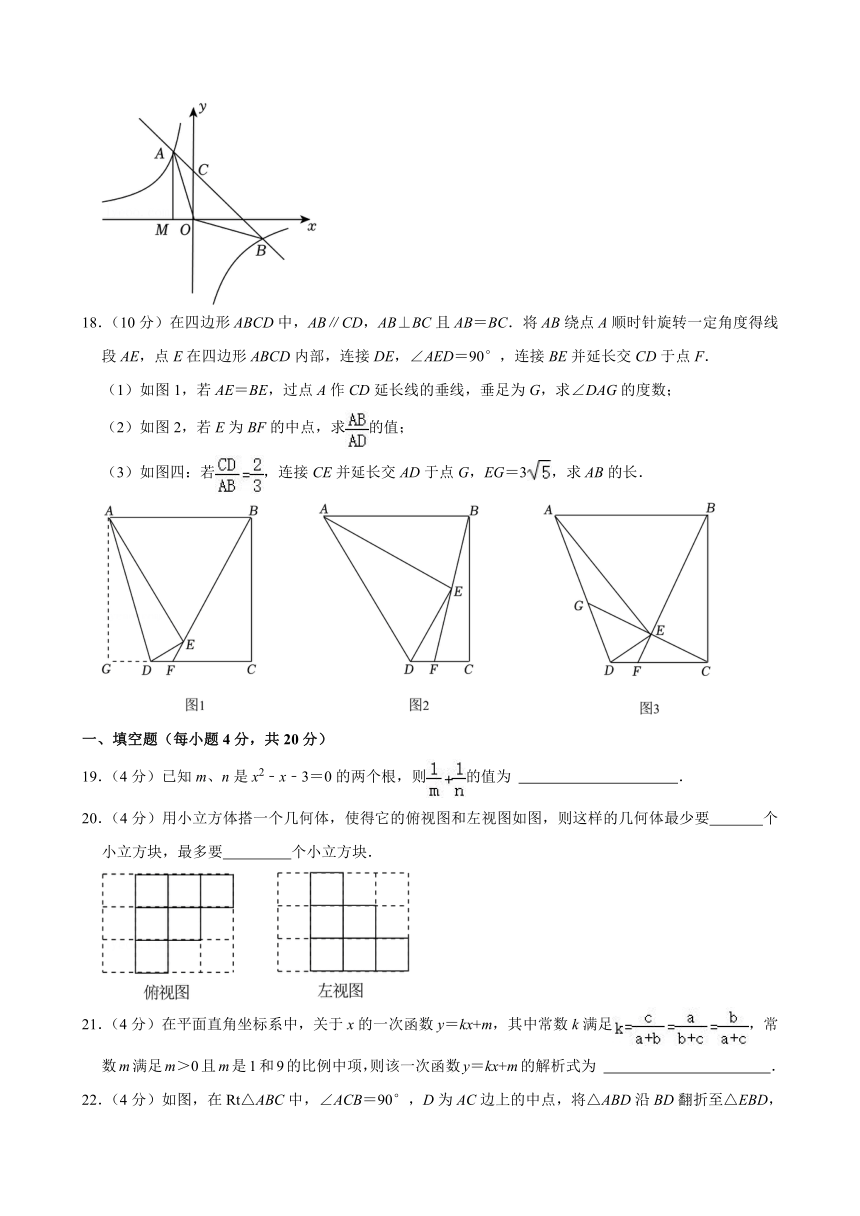
20.(4分)用小立方体搭一个几何体,使得它的俯视图和左视图如图,则这样的几何体最少要 个小立方块,最多要 个小立方块.
21.(4分)在平面直角坐标系中,关于x的一次函数y=kx+m,其中常数k满足,常数m满足m>0且m是1和9的比例中项,则该一次函数y=kx+m的解析式为 .
22.(4分)如图,在Rt△ABC中,∠ACB=90°,D为AC边上的中点,将△ABD沿BD翻折至△EBD,连接CE,若CE:BD=3:4,则= .
23.(4分)如图,在正方形ABCD中,AB=3,点E在边CD上运动,连接BE,AE,将AE绕点E顺时针旋转90°得到EF,连接AF,BF,则的最小值为 .
二、解答题(共30分)
24.(8分)“我运动,我健康,我快乐!”随着人们对身心健康的关注度越来越高.某市参加健身运动的人数逐年增多,从2021年的32万人增加到2023年的50万人.
(1)求该市参加健身运动人数的年均增长率;
(2)为支持市民的健身运动,市政府决定从A公司购买某种套装健身器材.该公司规定:若购买不超过100套,每套售价1600元;若超过100套,每增加10套,售价每套可降低40元.但最低售价不得少于1000元.已知市政府向该公司支付货款24万元,求购买的这种健身器材的套数.
25.(10分)如图,在平面直角坐标系xOy中,直线y=﹣x+m与直线y=2x相交于点A(2,a),与x轴交于点B(b,0),点C在反比例函数y=(k<0)图象上.
(1)求a,b,m的值;
(2)若O,A,B,C为顶点的四边形为平行四边形,求点C的坐标和k的值;
(3)过A,C两点的直线与x轴负半轴交于点D,点E与点D关于y轴对称.若有且只有一点C,使得△ABD与△ABE相似,求k的值.
26.(12分)如图,在菱形ABCD中,点E是BC边上一动点(且与点B、C不重合),连接AE交BD于点G.
(1)若AE⊥BC,∠BAE=18°,求∠BGE的度数;
(2)若AG=BG,求证BE2﹣GE2=AG GE;
(3)过点G作GM//BC交AB于点M,记.S△AMG为S1,S四边形DGEC为S2,BC=xBE,
①求证:;
②求y与x之间的函数关系式.
2024-2025学年四川省成都市锦江区盐道街中学九年级(上)期中数学试卷
参考答案
一、选择题(每小题4分。共32分)
1.(4分)如图所示,该几何体的俯视图是( )
A. B. C. D.
选:B.
2.(4分)下列各组线段(单位:m)中,成比例线段的是( )
A.3,4,5,6 B.1,3,5,7
C.2,3,4,6 D.0.2,0.3,0.4,0.5
选:C.
3.(4分)下列函数中,变量y是x的反比例函数的是( )
A. B. C. D.
选:A.
4.(4分)如图,平行四边形ABCD对角线AC,BD交于点O,请添加一个条件:( ),使得平行四边形ABCD是矩形.
A.AB=BC B.AC⊥BD C.AB=DC D.AC=BD
选:D.
5.(4分)甲、乙、丙、丁4名同学参加读书日志愿服务活动,甲同学是男生,乙、丙、丁同学都是女生,从这4名同学中随机抽取2名同学,则抽到的2名同学都是女生的概率为( )
A. B. C. D.
选:B.
6.(4分)如图,在长为32米、宽为20米的矩形地面上修筑同样宽的道路(图中阴影部分),余下部分种植草坪,要使草坪的面积为540平方米,设道路的宽x米,则可列方程为( )
A.32×20﹣32x﹣20x=540
B.(32﹣x)(20﹣x)+x2=540
C.32x+20x=540
D.(32﹣x)(20﹣x)=540
选:D.
7.(4分)已知(﹣5,y1)(﹣1,y2),(2,y3)都在双曲线y=(k>0)上,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y3<y1<y2 C.y2<y1<y3 D.y3<y2<y1
选:C.
8.(4分)如图,在△ABC中,AD是BC边上中线,F是线段AD上一点,且AF:FD=2:3,连接CF并延长交AB于E,则AE:EB等于( )
A.1:2 B.2:3 C.1:3 D.3:5
选:C.
二、填空题(每小题4分,共20分)
9.(4分)若2a=3b,则= .
【解答】解:∵2a=3b,
∴b=a,
∴===.
故答案为:.
10.(4分)已知关于x的方程(m﹣2)x|m|﹣3x﹣4=0是一元二次方程,则m= ﹣2 .
【解答】解:∵关于x的方程(m﹣2)x|m|﹣3x﹣4=0是一元二次方程,
∴,
解得m=﹣2,
故答案为:﹣2.
11.(4分)如图是初三某班学习小组设计用手电筒来测量逸夫楼高度的示意图.点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到逸夫楼CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=0.8m,BP=1.2m,PD=27m,那么逸夫楼的高度为 18 m.
【解答】解:根据题意得∠APB=∠CPD,
∵AB⊥BD,CD⊥BD,
∴∠ABP=∠CDP=90°,
∴△ABP∽△CDP,
∴=,即=,
解得:CD=18.
答:逸夫楼的高度约为18m.
故答案为:18.
12.(4分)如图,在△ADE中,BC∥DE,其中BC=2,DE=3,S△ABC=8,则S四边形BDEC= 10 .
【解答】解:∵DE∥BC,
∴△ADE∽△ABC,
∴===,
∵S△ABC=8,
∴S△ADE=18,
∴S四边形BDEC=S△ADE﹣S△ABC=18﹣8=10.
故答案为:10.
13.(4分)如图,BD是 ABCD的对角线,按以下步骤作图:①分别以点B和点D为圆心,
大于BD的长为半径作弧,两弧相交于E,F两点;②作直线EF,分别交AD,BC于点M,N,连接BM,DN.若BD=8,MN=6,则 ABCD的边BC上的高为 .
【解答】解:由作法得MN垂直平分BD,
∴MB=MD,NB=ND,
∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠MDB=∠NBD,
而MB=MD,
∴∠MBD=∠MDB,
∴∠MBD=∠NBD,
而BD⊥MN,
∴△BMN为等腰三角形,
∴BM=BN,
∴BM=BN=ND=MD,
∴四边形BMDN为菱形,
∴BN==5,
设 ABCD的边BC上的高为h,
∵MN BD=2BN h,
∴h==,
即 ABCD的边BC上的高为.
故答案为.
三、解答题(共48分)
14.(12分)(1)计算:;
(2)解方程:x2﹣4x+3=x;
(3)解方程:x2﹣4=5(x﹣2).
【解答】解:(1)
=4﹣1+2﹣﹣4
=1﹣;
(2)x2﹣4x+3=x,
x2﹣5x+3=0,
这里a=1,b=﹣5,c=3,
∴Δ=(﹣5)2﹣4×1×3=13>0,
∴x=,
∴x1=,x2=;
(3)x2﹣4=5(x﹣2),
(x+2)(x﹣2)﹣5(x﹣2)=0,
(x﹣2)(x+2﹣5)=0,
(x﹣2)(x﹣3)=0,
∴x﹣2=0或x﹣3=0,
∴x1=2,x2=3.
15.(8分)如图,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0),A(2,1),B(1,﹣2).
(1)画出将△OAB向左平移2个单位,再向上平移1个单位后得到的△O1A1B1;
(2)以原点O为位似中心,在y轴的右侧画出△OAB的一个位似△OA2B2,使它与△OAB的相似比为2:1;
(3)判断△O1A1B1和△OA2B2是否是位似图形(直接写结果),若是,请在图中标出位似中心点M,并写出点M的坐标.
【解答】解:(1)如图1,△O1A1B1即为所求.
(2)如图2,△OA2B2即为所求.
(3)△O1A1B1和△OA2B2是位似图形;理由如下:
如图3,
点M即为位似中心,M(﹣4,2).
16.(8分)为了贯彻落实健康第一的指导思想,促进学生全面发展,我校积极倡导人文运动观念,提高同学们的身体素质,现对七、八年级部分学生每周的锻炼时间(单位:h)进行统计,按照每周锻炼时间分成四组:A:0≤x<3;B:3≤x<6;C:6≤x<9;D:9≤x≤12,并绘制了如图两幅不完整的统计图,请你根据图中所提供的信息,完成下列问题:
(1)该校此次调查共抽取了 80 名学生,扇形统计图中“B”组对应的扇形圆心角的度数为 162 °,并补全条形统计图;
(2)若该校八年级共600名学生,请估计八年级每周锻炼时间达到6小时及以上的学生人数;
(3)若“D”组中七年级和八年级各有2名同学报名市区的运动比赛,学校打算从这4名同学中挑选2名参赛,请用列表法或树状图法求恰好选中七年级和八年级各1名同学的概率.
【解答】解:(1)该校此次调查共抽取了(10+6)÷20%=80(名)学生.
扇形统计图中“B”组对应的扇形圆心角的度数为360°×=162°.
故答案为:80;162;
C组中八年级的学生人数为80﹣10﹣6﹣16﹣20﹣6﹣8﹣4=10(人).
补全条形统计图如图①所示.
(2)600×=210(人).
∴估计八年级每周锻炼时间达到6小时及以上的学生人数约210人;
(3)将七年级的2名同学分别记为a,b,将八年级的2名同学分别记为c,d,
列表如下:
a b c d
a (a,b) (a,c) (a,d)
b (b,a) (b,c) (b,d)
c (c,a) (c,b) (c,d)
d (d,a) (d,b) (d,c)
共有12种等可能的结果,其中恰好选中七年级和八年级各1名同学的结果有:(a,c),(a,d),(b,c),(b,d),(c,a),(c,b),(d,a),(d,b),共8种,
∴恰好选中七年级和八年级各1名同学的概率为.
17.(10分)如图,在平面直角坐标系中,一次函数y1=mx+n的图象与反比例函数的图象交于第二、四象限内的A、B两点,与y轴交于点C,过点A作AM⊥x轴,垂足为M,AM=3,OM=1,点B的纵坐标为﹣1.
(1)求反比例函数表达式和一次函数的解析式;
(2)直接写出当y1>y2时,自变量x的取值范围;
(3)连接OA、OB,求△AOB的面积.
【解答】解:(1)根据题意可知,A(﹣1,3),
∵点A在反比例函数图象上,
∴k=﹣3,
∴反比例函数解析式为y=﹣,
当y=﹣1时,x=3,
∴B(3,﹣1),
∵点A(﹣1,3)、B(3,﹣1)在一次函数y1=mx+n的图象上,
,解得,
∴一次函数解析式为:y=﹣x+2.
(2)根据函数图象及交点坐标,不等式y1>y2自变量x的取值范围为:x<﹣1或0<x<3.
(3)由一次函数y=﹣x+2可知,C(0,2)即OC=2,
S△AOB=S△AOC+S△BOC==4.
18.(10分)在四边形ABCD中,AB∥CD,AB⊥BC且AB=BC.将AB绕点A顺时针旋转一定角度得线段AE,点E在四边形ABCD内部,连接DE,∠AED=90°,连接BE并延长交CD于点F.
(1)如图1,若AE=BE,过点A作CD延长线的垂线,垂足为G,求∠DAG的度数;
(2)如图2,若E为BF的中点,求的值;
(3)如图四:若,连接CE并延长交AD于点G,EG=3,求AB的长.
【解答】解:(1)∵AB绕点A顺时针旋转一定角度得线段AE,
∴AE=AB,
∵AB=BC,
∴AB=BE=AE,
∴△ABE为等边三角形,∠BAE=60°,
∵AE=BC,
∵∠AED=∠AGD=90°,
∴AE=AG,
∵AD=AD,
∴Rt△AED≌Rt△AGD(HL),
∴;
(2)由点E向AB作垂线,垂足为M,向CD作垂线,垂足为N,由A点作CD的垂线,交CD的延长线交于G点,如图,
设AB=AE=y,BM=CN=FN=x,
∵∠MEA+∠DEN=90°,∠MEA+∠MAE=90°,
∴∠DEM=∠EAM,
同理∠EDN=∠MEA,
故△AEM∽△DEN,
∴,
∴,
∴,
∴DE=2DN,
∴AE=2ME,
∴,
∴,
∴,
∴,
∴;
(3)如图,由点E向AB,CD作垂线,垂足为M,N,由A向CD作垂线,垂足为H,由G向下作垂线,垂足为I,连接GB,
设CN=x,CD=2y,AB=3y,
由题意可知∠AED=∠AHD=90°,,AE=AB=3y,
则,
∵AB=AE=BC=AH,
∴A,D,E,H四点共圆,
∴Rt△AED≌Rt△AHD(HL),
∴△AME∽△DNE,相似比为,
∴,
∴,,
∴,
∴,
∴,
∴10x=12y,
∴,
∴,,
∴,
∵GI=3DI,CI=2GI,
∴,
∴,
∴y=5,
∴AB=15.
一、填空题(每小题4分,共20分)
19.(4分)已知m、n是x2﹣x﹣3=0的两个根,则的值为 ﹣ .
【解答】解:∵m、n是方程x2﹣x﹣3=0的两个根,
∴m+n=1,mn=﹣3,
∴===﹣,
故答案为:﹣.
20.(4分)用小立方体搭一个几何体,使得它的俯视图和左视图如图,则这样的几何体最少要 9 个小立方块,最多要 14 个小立方块.
【解答】解:根据图形可知,几何体最底层有6个小立方块,第二层最少有2个小立方块,第三层最少有1个小立方块,
∴最少有6+2+1=9个小立方块;
根据图形可知,几何体最底层有6个小立方块,第二层最多有5个小立方块,第三层最多有3个小立方块,
∴最多有6+5+3=14个小立方块.
故答案为:9;14.
21.(4分)在平面直角坐标系中,关于x的一次函数y=kx+m,其中常数k满足,常数m满足m>0且m是1和9的比例中项,则该一次函数y=kx+m的解析式为 y=x+3或y=﹣x+3 .
【解答】解:∵常数m满足m>0且m是1和9的比例中项,
∴m=3,
∵,
∴c=k(a+b),a=k(b+c),b=k(a+c),
∴a+b+c=2k(a+b+c),
∴a+b+c=0或k=,
当a+b+c=0时,a+c=﹣b,则k==﹣1,
∴该一次函数的解析式为y=x+3或y=﹣x+3,
故答案为:y=x+3或y=﹣x+3.
22.(4分)如图,在Rt△ABC中,∠ACB=90°,D为AC边上的中点,将△ABD沿BD翻折至△EBD,连接CE,若CE:BD=3:4,则= .
【解答】解:如图所示,连接AE,延长BD,交AE于F,
由折叠可得,AD=ED,AB=EB,
∴BD垂直平分AE,即∠AFD=90°,
∵D为AC边上的中点,
∴AD=CD=ED,
∴∠AFD=∠AEC,
∴∠AEC=180°×=90°,
∴BD∥CE,
∴∠DBC=∠ECG,
过E作EG⊥BC,交BC的延长线于G,
则∠G=∠BCD=90°,
∴△BCD∽△CGE,
∴CE:BD=CG:BC=EG:DC=3:4,
设CG=3a,EG=3b,则BC=4a,CD=4b=AD,
Rt△ABC中,AB2=BC2+AC2=(4a)2+(8b)2,
Rt△BCE中,EB2=BG2+EG2=(7a)2+(3b)2,
∴(4a)2+(8b)2=(7a)2+(3b)2,
整理得a:b=:,
∴Rt△ABC中,tanA===.
故答案为:.
23.(4分)如图,在正方形ABCD中,AB=3,点E在边CD上运动,连接BE,AE,将AE绕点E顺时针旋转90°得到EF,连接AF,BF,则的最小值为 .
【解答】解:∵在正方形ABCD中,AB=3,点E在边CD上运动,连接BE,AE,将AE绕点E顺时针旋转90°得到EF,连接AF,BF,
∴AB=BC=3,∠ABC=∠BCE=90°,
将BE绕点E旋转90°得到EG,连接AG、BG,则∠BEG=90°,BE=EG,
∴,∠EBG=45°,
∴∠AEF=90°=∠BEG,AE=EF,
∴∠BEG+∠BEA=∠AEF+∠BEA,
即∠AEG=∠BEF,
∵BE=EG,AE=EF,
∴△BEF≌△GEA(SAS),
∴BF=AG,
∴,
将BC绕点C旋转90°,得到CH,连接BH、GH,
则BC=CH,,∠CBH=45°=∠EBG,
∴∠EAC=∠GBH=45°﹣∠CBG,
∵,,
∴,
∴△BHG∽△BCE,
∴∠BHG=∠BCE=90°,
∴点G在直线HG上运动,
作点B关于HG的对称点M,连接AM、GM,则,,
过点M作MN⊥AB,交AB的延长线于点N,则∠ANM=90°,∠CBN=90°,
∵∠CBH=45°,
∴∠MBN=45°,
∴△MBN为等腰直角三角形,
∴,
∴AN=AB+BN=6+3=9,
∴,
∴的最小值为,
故答案为:.
二、解答题(共30分)
24.(8分)“我运动,我健康,我快乐!”随着人们对身心健康的关注度越来越高.某市参加健身运动的人数逐年增多,从2021年的32万人增加到2023年的50万人.
(1)求该市参加健身运动人数的年均增长率;
(2)为支持市民的健身运动,市政府决定从A公司购买某种套装健身器材.该公司规定:若购买不超过100套,每套售价1600元;若超过100套,每增加10套,售价每套可降低40元.但最低售价不得少于1000元.已知市政府向该公司支付货款24万元,求购买的这种健身器材的套数.
【解答】解:(1)设该市参加健身运动人数的年均增长率为x,
由题意得:32(1+x)2=50,
解得:x1=0.25=25%,x2=﹣2.25(不符合题意,舍去),
答:该市参加健身运动人数的年均增长率为25%;
(2)设购买的这种健身器材的套数为m套,
由题意得:m(1600﹣×40)=240000,
整理得:m2﹣500m+60000=0,
解得:m1=200,m2=300(不符合题意,舍去),
答:购买的这种健身器材的套数为200套.
25.(10分)如图,在平面直角坐标系xOy中,直线y=﹣x+m与直线y=2x相交于点A(2,a),与x轴交于点B(b,0),点C在反比例函数y=(k<0)图象上.
(1)求a,b,m的值;
(2)若O,A,B,C为顶点的四边形为平行四边形,求点C的坐标和k的值;
(3)过A,C两点的直线与x轴负半轴交于点D,点E与点D关于y轴对称.若有且只有一点C,使得△ABD与△ABE相似,求k的值.
【解答】解:(1)把A(2,a)代入y=2x得:a=2×2=4,
∴A(2,4),
把A(2,4)代入y=﹣x+m得:4=﹣2+m,
∴m=6;
∴直线y=﹣x+m为y=﹣x+6,
把B(b,0)代入y=﹣x+6得:0=﹣b+6,
∴b=6,
∴a的值为4,m的值为6,b的值为6;
(2)设C(t,),
由(1)知A(2,4),B(6,0),而O(0,0),
①当AC,BO为对角线时,AC,BO的中点重合,
∴,
解得,
经检验,t=4,k=﹣16符合题意,
此时点C的坐标为(4,﹣4);
②当CB,AO为对角线时,CB,AO的中点重合,
∴,
解得,
经检验,t=﹣4,k=﹣16符合题意,
此时点C的坐标为(﹣4,4);
③当CO,AB为对角线时,CO,AB的中点重合,
∴,
解得,
∵k=32>0,
∴这种情况不符合题意;
综上所述,C的坐标为(4,﹣4)或(﹣4,4),k的值为﹣16;
(3)如图:
设直线AC解析式为y=px+q,把A(2,4)代入得:4=2p+q,
∴q=4﹣2p,
∴直线AC解析式为y=px+4﹣2p,
在y=px+4﹣2p中,令y=0得x=,
∴D(,0),
∵E与点D关于y轴对称,
∴E(,0),
∵B(6,0),
∴BE=6﹣=,BD=6﹣=,
∵△ABD与△ABE相似,
∴E只能在B左侧,
∴∠ABE=∠DBA,
故△ABD与△ABE相似,只需=即可,即BE BD=AB2,
∵A(2,4),B(6,0),
∴AB2=32,
∴×=32,
解得p=1,
经检验,p=1满足题意,
∴直线AC的解析式为y=x+2,
∵有且只有一点C,使得△ABD与△ABE相似,
∴直线AC与反比例函数y=(k<0)图象只有一个交点,
∴x+2=只有一个解,
即x2+2x﹣k=0有两个相等实数根,
∴Δ=0,即22+4k=0,
解得k=﹣1,
∴k的值为﹣1.
26.(12分)如图,在菱形ABCD中,点E是BC边上一动点(且与点B、C不重合),连接AE交BD于点G.
(1)若AE⊥BC,∠BAE=18°,求∠BGE的度数;
(2)若AG=BG,求证BE2﹣GE2=AG GE;
(3)过点G作GM//BC交AB于点M,记.S△AMG为S1,S四边形DGEC为S2,BC=xBE,
①求证:;
②求y与x之间的函数关系式.
【解答】(1)解:根据题意可得∠AEB=90°,∠BAE=18°,
∴∠ABE=90°﹣18°=72°,
∵四边形ABCD是菱形,
∴,
∴∠BGE=∠ABG+∠BAG=18°+36°=54°.
(2)证明:∵AG=BG,
∴∠ABG=∠BAG,
∵∠GBE=∠ABG,
∴∠GBE=∠BAG,
又∵∠AEB=∠GEB,
∴△AEB∽△BEG,
∴,
∴BE2=AE GE,
∴BE2=(AG+GE)GE,
∴BE2﹣GE2=AG GE.
(3)①证明:∵GM∥BC,BC∥AD,
∴MG∥AD,
∴△BMG∽△BAD,△AMG∽△ABE,
∴,,
两式相加得,
即,
∴.
②解:∵BC=xBE,AD∥BC,
∴,△ADG∽△EBG,
∴,
∴S△AGD=xS△ABG,
∴S△ABD=S△ABG+xS△ABG=(x+1)S△ABG,
∵四边形ABCD是菱形,
∴△ABD≌△BCD(SSS),
∴S△BDC=(x+1)S△ABG,
∵MG∥BE,∠MBG=∠GBE,
∴△AMG∽△ABE,∠MBG=∠GBE=∠MGB,
∴MG=MB,
∴,
∴,
∴,
∴S1=,,
∵S△BDC=(x+1)S△ABG,
∴,
∴,
∴.
一、选择题(每小题4分。共32分)
1.(4分)如图所示,该几何体的俯视图是( )
A. B. C. D.
2.(4分)下列各组线段(单位:m)中,成比例线段的是( )
A.3,4,5,6 B.1,3,5,7
C.2,3,4,6 D.0.2,0.3,0.4,0.5
3.(4分)下列函数中,变量y是x的反比例函数的是( )
A. B. C. D.
4.(4分)如图,平行四边形ABCD对角线AC,BD交于点O,请添加一个条件:( ),使得平行四边形ABCD是矩形.
A.AB=BC B.AC⊥BD C.AB=DC D.AC=BD
5.(4分)甲、乙、丙、丁4名同学参加读书日志愿服务活动,甲同学是男生,乙、丙、丁同学都是女生,从这4名同学中随机抽取2名同学,则抽到的2名同学都是女生的概率为( )
A. B. C. D.
6.(4分)如图,在长为32米、宽为20米的矩形地面上修筑同样宽的道路(图中阴影部分),余下部分种植草坪,要使草坪的面积为540平方米,设道路的宽x米,则可列方程为( )
A.32×20﹣32x﹣20x=540
B.(32﹣x)(20﹣x)+x2=540
C.32x+20x=540
D.(32﹣x)(20﹣x)=540
7.(4分)已知(﹣5,y1)(﹣1,y2),(2,y3)都在双曲线y=(k>0)上,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y3<y1<y2 C.y2<y1<y3 D.y3<y2<y1
8.(4分)如图,在△ABC中,AD是BC边上中线,F是线段AD上一点,且AF:FD=2:3,连接CF并延长交AB于E,则AE:EB等于( )
A.1:2 B.2:3 C.1:3 D.3:5
二、填空题(每小题4分,共20分)
9.(4分)若2a=3b,则= .
10.(4分)已知关于x的方程(m﹣2)x|m|﹣3x﹣4=0是一元二次方程,则m= .
11.(4分)如图是初三某班学习小组设计用手电筒来测量逸夫楼高度的示意图.点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到逸夫楼CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=0.8m,BP=1.2m,PD=27m,那么逸夫楼的高度为 m.
12.(4分)如图,在△ADE中,BC∥DE,其中BC=2,DE=3,S△ABC=8,则S四边形BDEC= .
13.(4分)如图,BD是 ABCD的对角线,按以下步骤作图:①分别以点B和点D为圆心,
大于BD的长为半径作弧,两弧相交于E,F两点;②作直线EF,分别交AD,BC于点M,N,连接BM,DN.若BD=8,MN=6,则 ABCD的边BC上的高为 .
三、解答题(共48分)
14.(12分)(1)计算:;
(2)解方程:x2﹣4x+3=x;
(3)解方程:x2﹣4=5(x﹣2).
15.(8分)如图,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0),A(2,1),B(1,﹣2).
(1)画出将△OAB向左平移2个单位,再向上平移1个单位后得到的△O1A1B1;
(2)以原点O为位似中心,在y轴的右侧画出△OAB的一个位似△OA2B2,使它与△OAB的相似比为2:1;
(3)判断△O1A1B1和△OA2B2是否是位似图形(直接写结果),若是,请在图中标出位似中心点M,并写出点M的坐标.
16.(8分)为了贯彻落实健康第一的指导思想,促进学生全面发展,我校积极倡导人文运动观念,提高同学们的身体素质,现对七、八年级部分学生每周的锻炼时间(单位:h)进行统计,按照每周锻炼时间分成四组:A:0≤x<3;B:3≤x<6;C:6≤x<9;D:9≤x≤12,并绘制了如图两幅不完整的统计图,请你根据图中所提供的信息,完成下列问题:
(1)该校此次调查共抽取了 名学生,扇形统计图中“B”组对应的扇形圆心角的度数为 °,并补全条形统计图;
(2)若该校八年级共600名学生,请估计八年级每周锻炼时间达到6小时及以上的学生人数;
(3)若“D”组中七年级和八年级各有2名同学报名市区的运动比赛,学校打算从这4名同学中挑选2名参赛,请用列表法或树状图法求恰好选中七年级和八年级各1名同学的概率.
17.(10分)如图,在平面直角坐标系中,一次函数y1=mx+n的图象与反比例函数的图象交于第二、四象限内的A、B两点,与y轴交于点C,过点A作AM⊥x轴,垂足为M,AM=3,OM=1,点B的纵坐标为﹣1.
(1)求反比例函数表达式和一次函数的解析式;
(2)直接写出当y1>y2时,自变量x的取值范围;
(3)连接OA、OB,求△AOB的面积.
18.(10分)在四边形ABCD中,AB∥CD,AB⊥BC且AB=BC.将AB绕点A顺时针旋转一定角度得线段AE,点E在四边形ABCD内部,连接DE,∠AED=90°,连接BE并延长交CD于点F.
(1)如图1,若AE=BE,过点A作CD延长线的垂线,垂足为G,求∠DAG的度数;
(2)如图2,若E为BF的中点,求的值;
(3)如图四:若,连接CE并延长交AD于点G,EG=3,求AB的长.
一、填空题(每小题4分,共20分)
19.(4分)已知m、n是x2﹣x﹣3=0的两个根,则的值为 .
20.(4分)用小立方体搭一个几何体,使得它的俯视图和左视图如图,则这样的几何体最少要 个小立方块,最多要 个小立方块.
21.(4分)在平面直角坐标系中,关于x的一次函数y=kx+m,其中常数k满足,常数m满足m>0且m是1和9的比例中项,则该一次函数y=kx+m的解析式为 .
22.(4分)如图,在Rt△ABC中,∠ACB=90°,D为AC边上的中点,将△ABD沿BD翻折至△EBD,连接CE,若CE:BD=3:4,则= .
23.(4分)如图,在正方形ABCD中,AB=3,点E在边CD上运动,连接BE,AE,将AE绕点E顺时针旋转90°得到EF,连接AF,BF,则的最小值为 .
二、解答题(共30分)
24.(8分)“我运动,我健康,我快乐!”随着人们对身心健康的关注度越来越高.某市参加健身运动的人数逐年增多,从2021年的32万人增加到2023年的50万人.
(1)求该市参加健身运动人数的年均增长率;
(2)为支持市民的健身运动,市政府决定从A公司购买某种套装健身器材.该公司规定:若购买不超过100套,每套售价1600元;若超过100套,每增加10套,售价每套可降低40元.但最低售价不得少于1000元.已知市政府向该公司支付货款24万元,求购买的这种健身器材的套数.
25.(10分)如图,在平面直角坐标系xOy中,直线y=﹣x+m与直线y=2x相交于点A(2,a),与x轴交于点B(b,0),点C在反比例函数y=(k<0)图象上.
(1)求a,b,m的值;
(2)若O,A,B,C为顶点的四边形为平行四边形,求点C的坐标和k的值;
(3)过A,C两点的直线与x轴负半轴交于点D,点E与点D关于y轴对称.若有且只有一点C,使得△ABD与△ABE相似,求k的值.
26.(12分)如图,在菱形ABCD中,点E是BC边上一动点(且与点B、C不重合),连接AE交BD于点G.
(1)若AE⊥BC,∠BAE=18°,求∠BGE的度数;
(2)若AG=BG,求证BE2﹣GE2=AG GE;
(3)过点G作GM//BC交AB于点M,记.S△AMG为S1,S四边形DGEC为S2,BC=xBE,
①求证:;
②求y与x之间的函数关系式.
2024-2025学年四川省成都市锦江区盐道街中学九年级(上)期中数学试卷
参考答案
一、选择题(每小题4分。共32分)
1.(4分)如图所示,该几何体的俯视图是( )
A. B. C. D.
选:B.
2.(4分)下列各组线段(单位:m)中,成比例线段的是( )
A.3,4,5,6 B.1,3,5,7
C.2,3,4,6 D.0.2,0.3,0.4,0.5
选:C.
3.(4分)下列函数中,变量y是x的反比例函数的是( )
A. B. C. D.
选:A.
4.(4分)如图,平行四边形ABCD对角线AC,BD交于点O,请添加一个条件:( ),使得平行四边形ABCD是矩形.
A.AB=BC B.AC⊥BD C.AB=DC D.AC=BD
选:D.
5.(4分)甲、乙、丙、丁4名同学参加读书日志愿服务活动,甲同学是男生,乙、丙、丁同学都是女生,从这4名同学中随机抽取2名同学,则抽到的2名同学都是女生的概率为( )
A. B. C. D.
选:B.
6.(4分)如图,在长为32米、宽为20米的矩形地面上修筑同样宽的道路(图中阴影部分),余下部分种植草坪,要使草坪的面积为540平方米,设道路的宽x米,则可列方程为( )
A.32×20﹣32x﹣20x=540
B.(32﹣x)(20﹣x)+x2=540
C.32x+20x=540
D.(32﹣x)(20﹣x)=540
选:D.
7.(4分)已知(﹣5,y1)(﹣1,y2),(2,y3)都在双曲线y=(k>0)上,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y3<y1<y2 C.y2<y1<y3 D.y3<y2<y1
选:C.
8.(4分)如图,在△ABC中,AD是BC边上中线,F是线段AD上一点,且AF:FD=2:3,连接CF并延长交AB于E,则AE:EB等于( )
A.1:2 B.2:3 C.1:3 D.3:5
选:C.
二、填空题(每小题4分,共20分)
9.(4分)若2a=3b,则= .
【解答】解:∵2a=3b,
∴b=a,
∴===.
故答案为:.
10.(4分)已知关于x的方程(m﹣2)x|m|﹣3x﹣4=0是一元二次方程,则m= ﹣2 .
【解答】解:∵关于x的方程(m﹣2)x|m|﹣3x﹣4=0是一元二次方程,
∴,
解得m=﹣2,
故答案为:﹣2.
11.(4分)如图是初三某班学习小组设计用手电筒来测量逸夫楼高度的示意图.点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到逸夫楼CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=0.8m,BP=1.2m,PD=27m,那么逸夫楼的高度为 18 m.
【解答】解:根据题意得∠APB=∠CPD,
∵AB⊥BD,CD⊥BD,
∴∠ABP=∠CDP=90°,
∴△ABP∽△CDP,
∴=,即=,
解得:CD=18.
答:逸夫楼的高度约为18m.
故答案为:18.
12.(4分)如图,在△ADE中,BC∥DE,其中BC=2,DE=3,S△ABC=8,则S四边形BDEC= 10 .
【解答】解:∵DE∥BC,
∴△ADE∽△ABC,
∴===,
∵S△ABC=8,
∴S△ADE=18,
∴S四边形BDEC=S△ADE﹣S△ABC=18﹣8=10.
故答案为:10.
13.(4分)如图,BD是 ABCD的对角线,按以下步骤作图:①分别以点B和点D为圆心,
大于BD的长为半径作弧,两弧相交于E,F两点;②作直线EF,分别交AD,BC于点M,N,连接BM,DN.若BD=8,MN=6,则 ABCD的边BC上的高为 .
【解答】解:由作法得MN垂直平分BD,
∴MB=MD,NB=ND,
∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠MDB=∠NBD,
而MB=MD,
∴∠MBD=∠MDB,
∴∠MBD=∠NBD,
而BD⊥MN,
∴△BMN为等腰三角形,
∴BM=BN,
∴BM=BN=ND=MD,
∴四边形BMDN为菱形,
∴BN==5,
设 ABCD的边BC上的高为h,
∵MN BD=2BN h,
∴h==,
即 ABCD的边BC上的高为.
故答案为.
三、解答题(共48分)
14.(12分)(1)计算:;
(2)解方程:x2﹣4x+3=x;
(3)解方程:x2﹣4=5(x﹣2).
【解答】解:(1)
=4﹣1+2﹣﹣4
=1﹣;
(2)x2﹣4x+3=x,
x2﹣5x+3=0,
这里a=1,b=﹣5,c=3,
∴Δ=(﹣5)2﹣4×1×3=13>0,
∴x=,
∴x1=,x2=;
(3)x2﹣4=5(x﹣2),
(x+2)(x﹣2)﹣5(x﹣2)=0,
(x﹣2)(x+2﹣5)=0,
(x﹣2)(x﹣3)=0,
∴x﹣2=0或x﹣3=0,
∴x1=2,x2=3.
15.(8分)如图,在平面直角坐标系中,△OAB的顶点坐标分别为O(0,0),A(2,1),B(1,﹣2).
(1)画出将△OAB向左平移2个单位,再向上平移1个单位后得到的△O1A1B1;
(2)以原点O为位似中心,在y轴的右侧画出△OAB的一个位似△OA2B2,使它与△OAB的相似比为2:1;
(3)判断△O1A1B1和△OA2B2是否是位似图形(直接写结果),若是,请在图中标出位似中心点M,并写出点M的坐标.
【解答】解:(1)如图1,△O1A1B1即为所求.
(2)如图2,△OA2B2即为所求.
(3)△O1A1B1和△OA2B2是位似图形;理由如下:
如图3,
点M即为位似中心,M(﹣4,2).
16.(8分)为了贯彻落实健康第一的指导思想,促进学生全面发展,我校积极倡导人文运动观念,提高同学们的身体素质,现对七、八年级部分学生每周的锻炼时间(单位:h)进行统计,按照每周锻炼时间分成四组:A:0≤x<3;B:3≤x<6;C:6≤x<9;D:9≤x≤12,并绘制了如图两幅不完整的统计图,请你根据图中所提供的信息,完成下列问题:
(1)该校此次调查共抽取了 80 名学生,扇形统计图中“B”组对应的扇形圆心角的度数为 162 °,并补全条形统计图;
(2)若该校八年级共600名学生,请估计八年级每周锻炼时间达到6小时及以上的学生人数;
(3)若“D”组中七年级和八年级各有2名同学报名市区的运动比赛,学校打算从这4名同学中挑选2名参赛,请用列表法或树状图法求恰好选中七年级和八年级各1名同学的概率.
【解答】解:(1)该校此次调查共抽取了(10+6)÷20%=80(名)学生.
扇形统计图中“B”组对应的扇形圆心角的度数为360°×=162°.
故答案为:80;162;
C组中八年级的学生人数为80﹣10﹣6﹣16﹣20﹣6﹣8﹣4=10(人).
补全条形统计图如图①所示.
(2)600×=210(人).
∴估计八年级每周锻炼时间达到6小时及以上的学生人数约210人;
(3)将七年级的2名同学分别记为a,b,将八年级的2名同学分别记为c,d,
列表如下:
a b c d
a (a,b) (a,c) (a,d)
b (b,a) (b,c) (b,d)
c (c,a) (c,b) (c,d)
d (d,a) (d,b) (d,c)
共有12种等可能的结果,其中恰好选中七年级和八年级各1名同学的结果有:(a,c),(a,d),(b,c),(b,d),(c,a),(c,b),(d,a),(d,b),共8种,
∴恰好选中七年级和八年级各1名同学的概率为.
17.(10分)如图,在平面直角坐标系中,一次函数y1=mx+n的图象与反比例函数的图象交于第二、四象限内的A、B两点,与y轴交于点C,过点A作AM⊥x轴,垂足为M,AM=3,OM=1,点B的纵坐标为﹣1.
(1)求反比例函数表达式和一次函数的解析式;
(2)直接写出当y1>y2时,自变量x的取值范围;
(3)连接OA、OB,求△AOB的面积.
【解答】解:(1)根据题意可知,A(﹣1,3),
∵点A在反比例函数图象上,
∴k=﹣3,
∴反比例函数解析式为y=﹣,
当y=﹣1时,x=3,
∴B(3,﹣1),
∵点A(﹣1,3)、B(3,﹣1)在一次函数y1=mx+n的图象上,
,解得,
∴一次函数解析式为:y=﹣x+2.
(2)根据函数图象及交点坐标,不等式y1>y2自变量x的取值范围为:x<﹣1或0<x<3.
(3)由一次函数y=﹣x+2可知,C(0,2)即OC=2,
S△AOB=S△AOC+S△BOC==4.
18.(10分)在四边形ABCD中,AB∥CD,AB⊥BC且AB=BC.将AB绕点A顺时针旋转一定角度得线段AE,点E在四边形ABCD内部,连接DE,∠AED=90°,连接BE并延长交CD于点F.
(1)如图1,若AE=BE,过点A作CD延长线的垂线,垂足为G,求∠DAG的度数;
(2)如图2,若E为BF的中点,求的值;
(3)如图四:若,连接CE并延长交AD于点G,EG=3,求AB的长.
【解答】解:(1)∵AB绕点A顺时针旋转一定角度得线段AE,
∴AE=AB,
∵AB=BC,
∴AB=BE=AE,
∴△ABE为等边三角形,∠BAE=60°,
∵AE=BC,
∵∠AED=∠AGD=90°,
∴AE=AG,
∵AD=AD,
∴Rt△AED≌Rt△AGD(HL),
∴;
(2)由点E向AB作垂线,垂足为M,向CD作垂线,垂足为N,由A点作CD的垂线,交CD的延长线交于G点,如图,
设AB=AE=y,BM=CN=FN=x,
∵∠MEA+∠DEN=90°,∠MEA+∠MAE=90°,
∴∠DEM=∠EAM,
同理∠EDN=∠MEA,
故△AEM∽△DEN,
∴,
∴,
∴,
∴DE=2DN,
∴AE=2ME,
∴,
∴,
∴,
∴,
∴;
(3)如图,由点E向AB,CD作垂线,垂足为M,N,由A向CD作垂线,垂足为H,由G向下作垂线,垂足为I,连接GB,
设CN=x,CD=2y,AB=3y,
由题意可知∠AED=∠AHD=90°,,AE=AB=3y,
则,
∵AB=AE=BC=AH,
∴A,D,E,H四点共圆,
∴Rt△AED≌Rt△AHD(HL),
∴△AME∽△DNE,相似比为,
∴,
∴,,
∴,
∴,
∴,
∴10x=12y,
∴,
∴,,
∴,
∵GI=3DI,CI=2GI,
∴,
∴,
∴y=5,
∴AB=15.
一、填空题(每小题4分,共20分)
19.(4分)已知m、n是x2﹣x﹣3=0的两个根,则的值为 ﹣ .
【解答】解:∵m、n是方程x2﹣x﹣3=0的两个根,
∴m+n=1,mn=﹣3,
∴===﹣,
故答案为:﹣.
20.(4分)用小立方体搭一个几何体,使得它的俯视图和左视图如图,则这样的几何体最少要 9 个小立方块,最多要 14 个小立方块.
【解答】解:根据图形可知,几何体最底层有6个小立方块,第二层最少有2个小立方块,第三层最少有1个小立方块,
∴最少有6+2+1=9个小立方块;
根据图形可知,几何体最底层有6个小立方块,第二层最多有5个小立方块,第三层最多有3个小立方块,
∴最多有6+5+3=14个小立方块.
故答案为:9;14.
21.(4分)在平面直角坐标系中,关于x的一次函数y=kx+m,其中常数k满足,常数m满足m>0且m是1和9的比例中项,则该一次函数y=kx+m的解析式为 y=x+3或y=﹣x+3 .
【解答】解:∵常数m满足m>0且m是1和9的比例中项,
∴m=3,
∵,
∴c=k(a+b),a=k(b+c),b=k(a+c),
∴a+b+c=2k(a+b+c),
∴a+b+c=0或k=,
当a+b+c=0时,a+c=﹣b,则k==﹣1,
∴该一次函数的解析式为y=x+3或y=﹣x+3,
故答案为:y=x+3或y=﹣x+3.
22.(4分)如图,在Rt△ABC中,∠ACB=90°,D为AC边上的中点,将△ABD沿BD翻折至△EBD,连接CE,若CE:BD=3:4,则= .
【解答】解:如图所示,连接AE,延长BD,交AE于F,
由折叠可得,AD=ED,AB=EB,
∴BD垂直平分AE,即∠AFD=90°,
∵D为AC边上的中点,
∴AD=CD=ED,
∴∠AFD=∠AEC,
∴∠AEC=180°×=90°,
∴BD∥CE,
∴∠DBC=∠ECG,
过E作EG⊥BC,交BC的延长线于G,
则∠G=∠BCD=90°,
∴△BCD∽△CGE,
∴CE:BD=CG:BC=EG:DC=3:4,
设CG=3a,EG=3b,则BC=4a,CD=4b=AD,
Rt△ABC中,AB2=BC2+AC2=(4a)2+(8b)2,
Rt△BCE中,EB2=BG2+EG2=(7a)2+(3b)2,
∴(4a)2+(8b)2=(7a)2+(3b)2,
整理得a:b=:,
∴Rt△ABC中,tanA===.
故答案为:.
23.(4分)如图,在正方形ABCD中,AB=3,点E在边CD上运动,连接BE,AE,将AE绕点E顺时针旋转90°得到EF,连接AF,BF,则的最小值为 .
【解答】解:∵在正方形ABCD中,AB=3,点E在边CD上运动,连接BE,AE,将AE绕点E顺时针旋转90°得到EF,连接AF,BF,
∴AB=BC=3,∠ABC=∠BCE=90°,
将BE绕点E旋转90°得到EG,连接AG、BG,则∠BEG=90°,BE=EG,
∴,∠EBG=45°,
∴∠AEF=90°=∠BEG,AE=EF,
∴∠BEG+∠BEA=∠AEF+∠BEA,
即∠AEG=∠BEF,
∵BE=EG,AE=EF,
∴△BEF≌△GEA(SAS),
∴BF=AG,
∴,
将BC绕点C旋转90°,得到CH,连接BH、GH,
则BC=CH,,∠CBH=45°=∠EBG,
∴∠EAC=∠GBH=45°﹣∠CBG,
∵,,
∴,
∴△BHG∽△BCE,
∴∠BHG=∠BCE=90°,
∴点G在直线HG上运动,
作点B关于HG的对称点M,连接AM、GM,则,,
过点M作MN⊥AB,交AB的延长线于点N,则∠ANM=90°,∠CBN=90°,
∵∠CBH=45°,
∴∠MBN=45°,
∴△MBN为等腰直角三角形,
∴,
∴AN=AB+BN=6+3=9,
∴,
∴的最小值为,
故答案为:.
二、解答题(共30分)
24.(8分)“我运动,我健康,我快乐!”随着人们对身心健康的关注度越来越高.某市参加健身运动的人数逐年增多,从2021年的32万人增加到2023年的50万人.
(1)求该市参加健身运动人数的年均增长率;
(2)为支持市民的健身运动,市政府决定从A公司购买某种套装健身器材.该公司规定:若购买不超过100套,每套售价1600元;若超过100套,每增加10套,售价每套可降低40元.但最低售价不得少于1000元.已知市政府向该公司支付货款24万元,求购买的这种健身器材的套数.
【解答】解:(1)设该市参加健身运动人数的年均增长率为x,
由题意得:32(1+x)2=50,
解得:x1=0.25=25%,x2=﹣2.25(不符合题意,舍去),
答:该市参加健身运动人数的年均增长率为25%;
(2)设购买的这种健身器材的套数为m套,
由题意得:m(1600﹣×40)=240000,
整理得:m2﹣500m+60000=0,
解得:m1=200,m2=300(不符合题意,舍去),
答:购买的这种健身器材的套数为200套.
25.(10分)如图,在平面直角坐标系xOy中,直线y=﹣x+m与直线y=2x相交于点A(2,a),与x轴交于点B(b,0),点C在反比例函数y=(k<0)图象上.
(1)求a,b,m的值;
(2)若O,A,B,C为顶点的四边形为平行四边形,求点C的坐标和k的值;
(3)过A,C两点的直线与x轴负半轴交于点D,点E与点D关于y轴对称.若有且只有一点C,使得△ABD与△ABE相似,求k的值.
【解答】解:(1)把A(2,a)代入y=2x得:a=2×2=4,
∴A(2,4),
把A(2,4)代入y=﹣x+m得:4=﹣2+m,
∴m=6;
∴直线y=﹣x+m为y=﹣x+6,
把B(b,0)代入y=﹣x+6得:0=﹣b+6,
∴b=6,
∴a的值为4,m的值为6,b的值为6;
(2)设C(t,),
由(1)知A(2,4),B(6,0),而O(0,0),
①当AC,BO为对角线时,AC,BO的中点重合,
∴,
解得,
经检验,t=4,k=﹣16符合题意,
此时点C的坐标为(4,﹣4);
②当CB,AO为对角线时,CB,AO的中点重合,
∴,
解得,
经检验,t=﹣4,k=﹣16符合题意,
此时点C的坐标为(﹣4,4);
③当CO,AB为对角线时,CO,AB的中点重合,
∴,
解得,
∵k=32>0,
∴这种情况不符合题意;
综上所述,C的坐标为(4,﹣4)或(﹣4,4),k的值为﹣16;
(3)如图:
设直线AC解析式为y=px+q,把A(2,4)代入得:4=2p+q,
∴q=4﹣2p,
∴直线AC解析式为y=px+4﹣2p,
在y=px+4﹣2p中,令y=0得x=,
∴D(,0),
∵E与点D关于y轴对称,
∴E(,0),
∵B(6,0),
∴BE=6﹣=,BD=6﹣=,
∵△ABD与△ABE相似,
∴E只能在B左侧,
∴∠ABE=∠DBA,
故△ABD与△ABE相似,只需=即可,即BE BD=AB2,
∵A(2,4),B(6,0),
∴AB2=32,
∴×=32,
解得p=1,
经检验,p=1满足题意,
∴直线AC的解析式为y=x+2,
∵有且只有一点C,使得△ABD与△ABE相似,
∴直线AC与反比例函数y=(k<0)图象只有一个交点,
∴x+2=只有一个解,
即x2+2x﹣k=0有两个相等实数根,
∴Δ=0,即22+4k=0,
解得k=﹣1,
∴k的值为﹣1.
26.(12分)如图,在菱形ABCD中,点E是BC边上一动点(且与点B、C不重合),连接AE交BD于点G.
(1)若AE⊥BC,∠BAE=18°,求∠BGE的度数;
(2)若AG=BG,求证BE2﹣GE2=AG GE;
(3)过点G作GM//BC交AB于点M,记.S△AMG为S1,S四边形DGEC为S2,BC=xBE,
①求证:;
②求y与x之间的函数关系式.
【解答】(1)解:根据题意可得∠AEB=90°,∠BAE=18°,
∴∠ABE=90°﹣18°=72°,
∵四边形ABCD是菱形,
∴,
∴∠BGE=∠ABG+∠BAG=18°+36°=54°.
(2)证明:∵AG=BG,
∴∠ABG=∠BAG,
∵∠GBE=∠ABG,
∴∠GBE=∠BAG,
又∵∠AEB=∠GEB,
∴△AEB∽△BEG,
∴,
∴BE2=AE GE,
∴BE2=(AG+GE)GE,
∴BE2﹣GE2=AG GE.
(3)①证明:∵GM∥BC,BC∥AD,
∴MG∥AD,
∴△BMG∽△BAD,△AMG∽△ABE,
∴,,
两式相加得,
即,
∴.
②解:∵BC=xBE,AD∥BC,
∴,△ADG∽△EBG,
∴,
∴S△AGD=xS△ABG,
∴S△ABD=S△ABG+xS△ABG=(x+1)S△ABG,
∵四边形ABCD是菱形,
∴△ABD≌△BCD(SSS),
∴S△BDC=(x+1)S△ABG,
∵MG∥BE,∠MBG=∠GBE,
∴△AMG∽△ABE,∠MBG=∠GBE=∠MGB,
∴MG=MB,
∴,
∴,
∴,
∴S1=,,
∵S△BDC=(x+1)S△ABG,
∴,
∴,
∴.
同课章节目录
