2024-2025学年云南省昆明八中八年级(上)期中数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年云南省昆明八中八年级(上)期中数学试卷(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 951.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-26 22:41:10 | ||
图片预览


文档简介
2024-2025学年云南省昆明八中八年级(上)期中数学试卷
一、选择题(本大题共15小题,每小题2分,共30分.在每小题给出的四个选项中,只有一项将合题目要求)
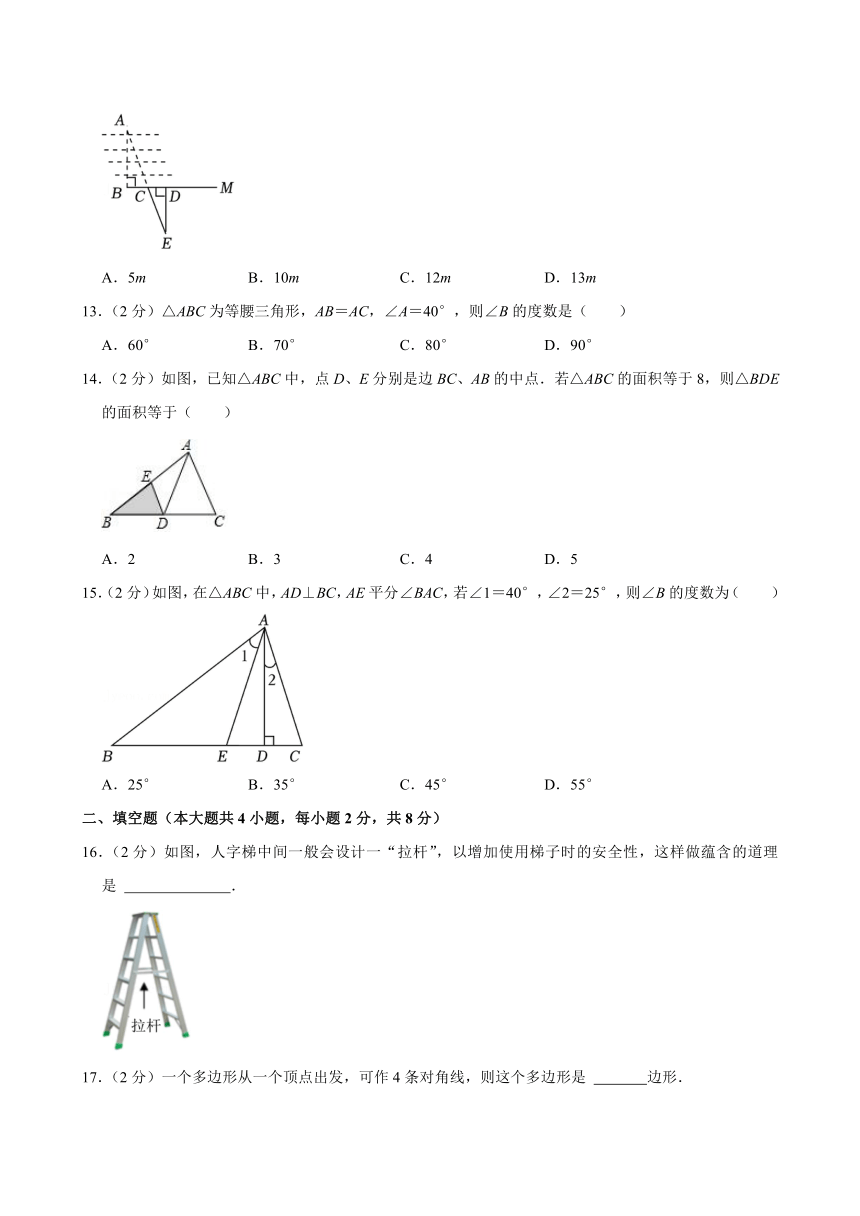
1.(2分)在数学活动课中,同学们利用几何画板绘制出了下列曲线,其中不是轴对称图形的是( )
A.等角螺旋线 B.心形线
C.四叶玫瑰线 D.蝴蝶曲线
2.(2分)以下列各组线段为边,其中能组成三角形的是( )
A.2,2,4 B.4,6,11 C.2,3,8 D.3,5,6
3.(2分)如图所示,△ABC中AC边上的高线是( )
A.线段HA B.线段BH C.线段BC D.线段BA
4.(2分)若直角三角形的一个锐角等于40°,则它的另一个锐角等于( )
A.50° B.60° C.70° D.140°
5.(2分)如图,在△ABC中,∠A=55°,∠B=45°,那么∠ACD的度数为( )
A.110 B.100 C.55 D.45
6.(2分)如图,图中三角形的个数为( )
A.3个 B.4个 C.5个 D.6个
7.(2分)在平面直角坐标系中,点P(2,1)关于y轴对称的点的坐标为( )
A.(2,﹣1) B.(﹣2,1) C.(﹣2,﹣1) D.(1,2)
8.(2分)如图,在△ABC中,AB=AC,D是边BC的中点,若∠BAC=80°,则∠ABC的度数为( )
A.23° B.20° C.50° D.100°
9.(2分)下列说法正确的是( )
A.直角三角形只有一条高
B.多边形的边数越多,其外角和就越大
C.三角形的三条中线都在三角形内部,且交于一点
D.三角形越大,它的内角和就越大
10.(2分)如图,△ABC与△A′B′C′关于直线l对称,若∠A=65°,∠C′=38°,则∠B的度数为( )
A.77° B.38° C.74° D.68°
11.(2分)如图,∠α的度数为( )
A.30° B.40° C.50° D.60°
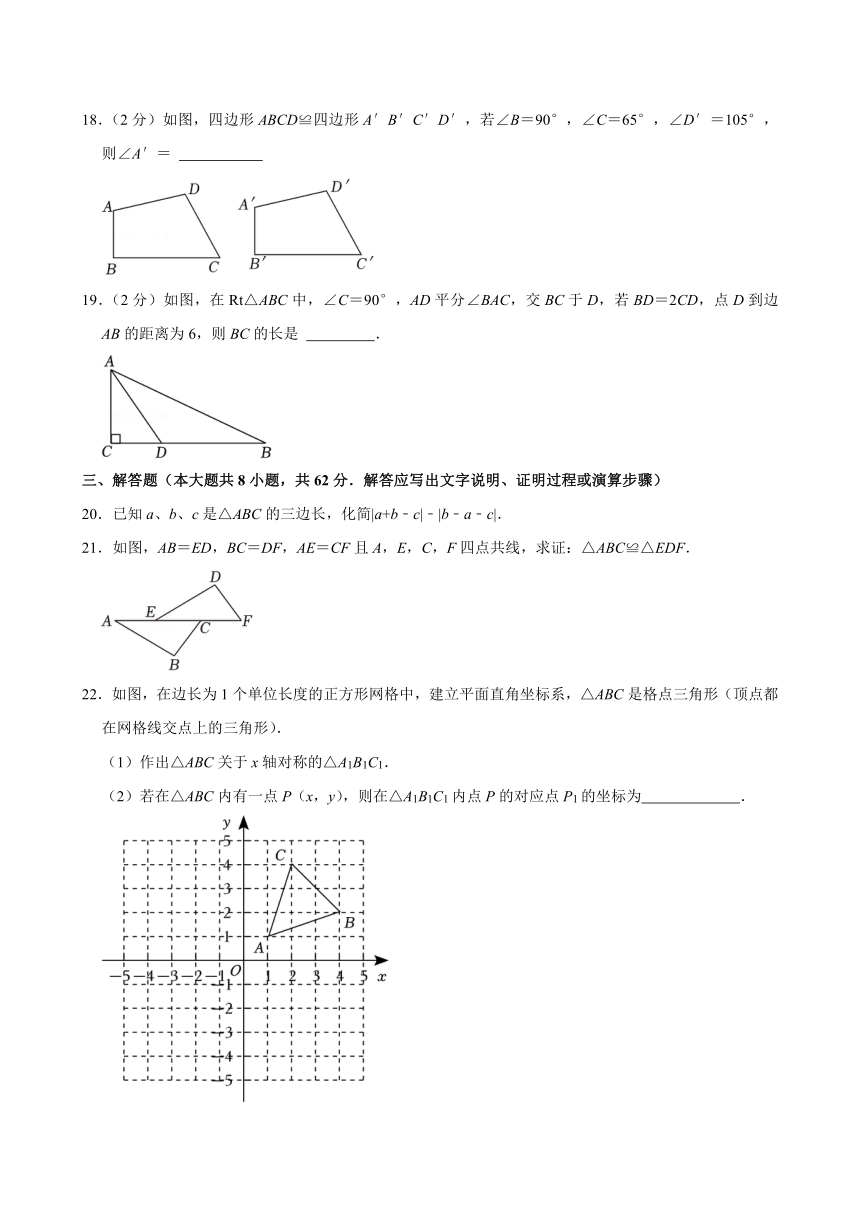
12.(2分)如图,要测量河两岸相对的两点A,B的距离,可在河的一侧取AB的垂线BM上两点C,D,使BC=CD,再画出BM的垂线DE,使E在AC的延长线上,若BD=10m,DE=12m,CE=13m,则A,B两点的距离是( )
A.5m B.10m C.12m D.13m
13.(2分)△ABC为等腰三角形,AB=AC,∠A=40°,则∠B的度数是( )
A.60° B.70° C.80° D.90°
14.(2分)如图,已知△ABC中,点D、E分别是边BC、AB的中点.若△ABC的面积等于8,则△BDE的面积等于( )
A.2 B.3 C.4 D.5
15.(2分)如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=40°,∠2=25°,则∠B的度数为( )
A.25° B.35° C.45° D.55°
二、填空题(本大题共4小题,每小题2分,共8分)
16.(2分)如图,人字梯中间一般会设计一“拉杆”,以增加使用梯子时的安全性,这样做蕴含的道理是 .
17.(2分)一个多边形从一个顶点出发,可作4条对角线,则这个多边形是 边形.
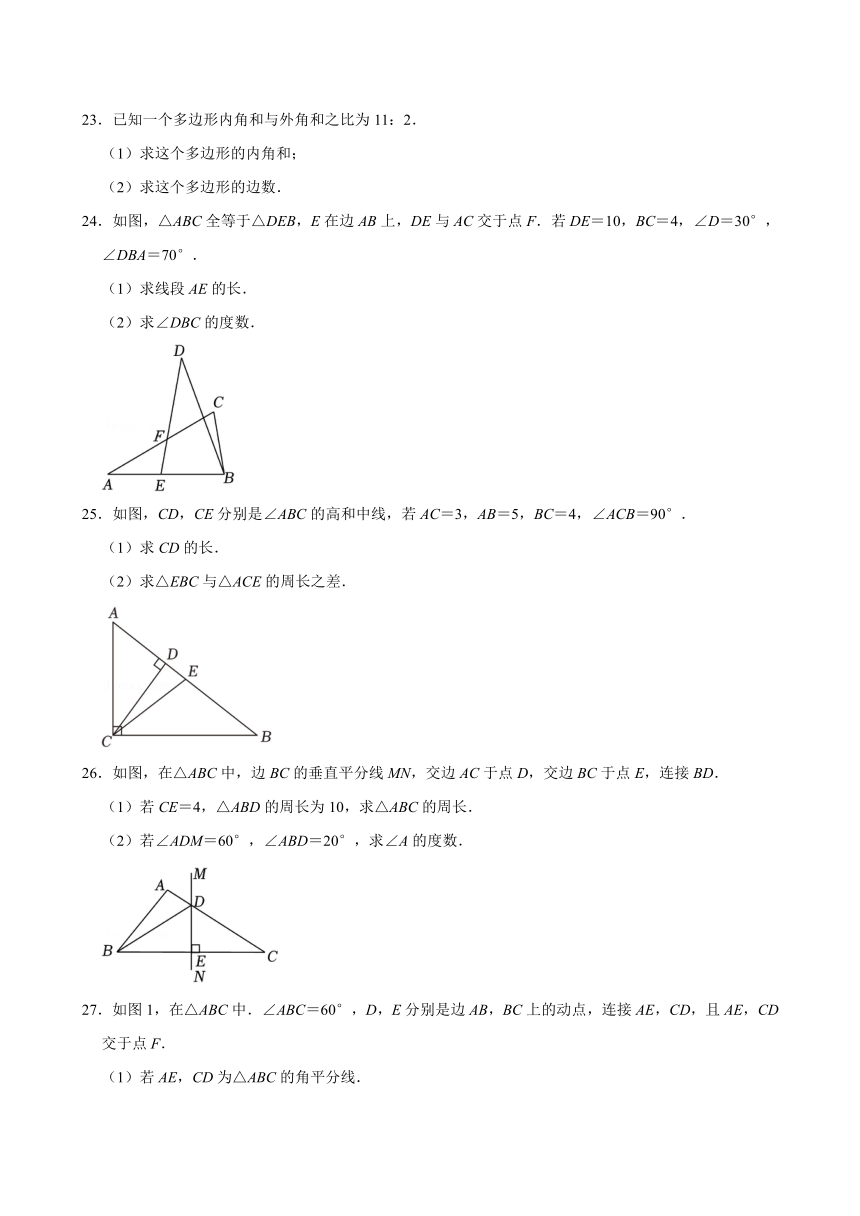
18.(2分)如图,四边形ABCD≌四边形A′B′C′D′,若∠B=90°,∠C=65°,∠D′=105°,则∠A′=
19.(2分)如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于D,若BD=2CD,点D到边AB的距离为6,则BC的长是 .
三、解答题(本大题共8小题,共62分.解答应写出文字说明、证明过程或演算步骤)
20.已知a、b、c是△ABC的三边长,化简|a+b﹣c|﹣|b﹣a﹣c|.
21.如图,AB=ED,BC=DF,AE=CF且A,E,C,F四点共线,求证:△ABC≌△EDF.
22.如图,在边长为1个单位长度的正方形网格中,建立平面直角坐标系,△ABC是格点三角形(顶点都在网格线交点上的三角形).
(1)作出△ABC关于x轴对称的△A1B1C1.
(2)若在△ABC内有一点P(x,y),则在△A1B1C1内点P的对应点P1的坐标为 .
23.已知一个多边形内角和与外角和之比为11:2.
(1)求这个多边形的内角和;
(2)求这个多边形的边数.
24.如图,△ABC全等于△DEB,E在边AB上,DE与AC交于点F.若DE=10,BC=4,∠D=30°,∠DBA=70°.
(1)求线段AE的长.
(2)求∠DBC的度数.
25.如图,CD,CE分别是∠ABC的高和中线,若AC=3,AB=5,BC=4,∠ACB=90°.
(1)求CD的长.
(2)求△EBC与△ACE的周长之差.
26.如图,在△ABC中,边BC的垂直平分线MN,交边AC于点D,交边BC于点E,连接BD.
(1)若CE=4,△ABD的周长为10,求△ABC的周长.
(2)若∠ADM=60°,∠ABD=20°,求∠A的度数.
27.如图1,在△ABC中.∠ABC=60°,D,E分别是边AB,BC上的动点,连接AE,CD,且AE,CD交于点F.
(1)若AE,CD为△ABC的角平分线.
①求∠AFC的度数.
②求证:AC=AD+CE.
(2)如图2.若AD=CE,∠ACD=∠CAE,求∠AFC的度数.
2024-2025学年云南省昆明八中八年级(上)期中数学试卷
参考答案
一、选择题(本大题共15小题,每小题2分,共30分.在每小题给出的四个选项中,只有一项将合题目要求)
1.(2分)在数学活动课中,同学们利用几何画板绘制出了下列曲线,其中不是轴对称图形的是( )
A.等角螺旋线 B.心形线
C.四叶玫瑰线 D.蝴蝶曲线
选:A.
2.(2分)以下列各组线段为边,其中能组成三角形的是( )
A.2,2,4 B.4,6,11 C.2,3,8 D.3,5,6
选:D.
3.(2分)如图所示,△ABC中AC边上的高线是( )
A.线段HA B.线段BH C.线段BC D.线段BA
选:B.
4.(2分)若直角三角形的一个锐角等于40°,则它的另一个锐角等于( )
A.50° B.60° C.70° D.140°
选:A.
5.(2分)如图,在△ABC中,∠A=55°,∠B=45°,那么∠ACD的度数为( )
A.110 B.100 C.55 D.45
选:B.
6.(2分)如图,图中三角形的个数为( )
A.3个 B.4个 C.5个 D.6个
选:C.
7.(2分)在平面直角坐标系中,点P(2,1)关于y轴对称的点的坐标为( )
A.(2,﹣1) B.(﹣2,1) C.(﹣2,﹣1) D.(1,2)
选:B.
8.(2分)如图,在△ABC中,AB=AC,D是边BC的中点,若∠BAC=80°,则∠ABC的度数为( )
A.23° B.20° C.50° D.100°
选:C.
9.(2分)下列说法正确的是( )
A.直角三角形只有一条高
B.多边形的边数越多,其外角和就越大
C.三角形的三条中线都在三角形内部,且交于一点
D.三角形越大,它的内角和就越大
选:C.
10.(2分)如图,△ABC与△A′B′C′关于直线l对称,若∠A=65°,∠C′=38°,则∠B的度数为( )
A.77° B.38° C.74° D.68°
选:A.
11.(2分)如图,∠α的度数为( )
A.30° B.40° C.50° D.60°
选:B.
12.(2分)如图,要测量河两岸相对的两点A,B的距离,可在河的一侧取AB的垂线BM上两点C,D,使BC=CD,再画出BM的垂线DE,使E在AC的延长线上,若BD=10m,DE=12m,CE=13m,则A,B两点的距离是( )
A.5m B.10m C.12m D.13m
选:C.
13.(2分)△ABC为等腰三角形,AB=AC,∠A=40°,则∠B的度数是( )
A.60° B.70° C.80° D.90°
选:B.
14.(2分)如图,已知△ABC中,点D、E分别是边BC、AB的中点.若△ABC的面积等于8,则△BDE的面积等于( )
A.2 B.3 C.4 D.5
选:A.
15.(2分)如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=40°,∠2=25°,则∠B的度数为( )
A.25° B.35° C.45° D.55°
选:B.
二、填空题(本大题共4小题,每小题2分,共8分)
16.(2分)如图,人字梯中间一般会设计一“拉杆”,以增加使用梯子时的安全性,这样做蕴含的道理是 三角形的稳定性 .
17.(2分)一个多边形从一个顶点出发,可作4条对角线,则这个多边形是 7 边形.
18.(2分)如图,四边形ABCD≌四边形A′B′C′D′,若∠B=90°,∠C=65°,∠D′=105°,则∠A′= 100°
19.(2分)如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于D,若BD=2CD,点D到边AB的距离为6,则BC的长是 18 .
三、解答题(本大题共8小题,共62分.解答应写出文字说明、证明过程或演算步骤)
20.已知a、b、c是△ABC的三边长,化简|a+b﹣c|﹣|b﹣a﹣c|.
【解答】解:∵a、b、c为△ABC的三条边长,
∴a+b﹣c>0,b﹣a﹣c<0,
|a+b﹣c|﹣|b﹣a﹣c|
=a+b﹣c﹣c﹣a+b
=2b﹣2c.
故答案为:2b﹣2c.
21.如图,AB=ED,BC=DF,AE=CF且A,E,C,F四点共线,求证:△ABC≌△EDF.
【解答】证明:∵AE=CF,
∴AE+EC=CF+EC,即AC=EF,
在△ABC和△EDF中,
,
∴△ABC≌△EDF(SSS).
22.如图,在边长为1个单位长度的正方形网格中,建立平面直角坐标系,△ABC是格点三角形(顶点都在网格线交点上的三角形).
(1)作出△ABC关于x轴对称的△A1B1C1.
(2)若在△ABC内有一点P(x,y),则在△A1B1C1内点P的对应点P1的坐标为 (x,﹣y) .
【解答】解:(1)如图,△A1B1C1即为所作.
(2)∵△ABC与△A1B1C1关于x轴对称,点P(x,y)是△ABC内一点,
∴在△A1B1C1内点P的对应点P1的坐标为(x,﹣y),
故答案为:(x,﹣y).
23.已知一个多边形内角和与外角和之比为11:2.
(1)求这个多边形的内角和;
(2)求这个多边形的边数.
【解答】解:(1)360°×=1980°,
答:这个多边形的内角和为1980°;
(2)设该多边形的边数为n
则(n﹣2)×180=360×
解得:n=13.
答:这个多边形的边数为13.
24.如图,△ABC全等于△DEB,E在边AB上,DE与AC交于点F.若DE=10,BC=4,∠D=30°,∠DBA=70°.
(1)求线段AE的长.
(2)求∠DBC的度数.
【解答】解:(1)∵DE=10,BC=4,
∴DE≠BC,
如图所示,BE为△DBE中的最短边,BC为△ABC中的最短边,
∵∠ABC>∠DBE,
∴DE和AC不可能是全等三角形的对应边,
∵E在边AB上,
∴AB≠BE,
∵△ABC全等于△DEB,
∴△ABC≌△DEB,
∴AB=DE=10,BE=BC=4,
∴AE=AB﹣BE=6;
(2)∵△ABC≌△DEB,∠D=30°,∠DBA=70°,
∴∠BAC=∠D=30°,∠DBA=∠C=70°,
∴∠ABC=180°﹣30°﹣70°=80°,
∴∠DBC=∠ABC﹣∠DBE=10°.
25.如图,CD,CE分别是∠ABC的高和中线,若AC=3,AB=5,BC=4,∠ACB=90°.
(1)求CD的长.
(2)求△EBC与△ACE的周长之差.
【解答】解:(1)∵,
∴;
(2)∵∠ABC的中线是CE,
∴AE=BE;
∴△EBC与△ACE的周长之差为:
BE+CE+BC﹣(AC+CE+AE)=BC﹣AC=4﹣3=1.
26.如图,在△ABC中,边BC的垂直平分线MN,交边AC于点D,交边BC于点E,连接BD.
(1)若CE=4,△ABD的周长为10,求△ABC的周长.
(2)若∠ADM=60°,∠ABD=20°,求∠A的度数.
【解答】解:(1)∵MN垂直平分BC,CE=4,
∴DC=DB,BE=CE=4,
∴BC=BE+CE=4+4=8,
∵△ABD的周长为10,
∴10=AB+AD+DB=AB+AD+DC=AB+AC,
∴AB+AC+BC=10+8=18,
∴△ABC的周长为18;
(2)∵∠ADM=60°,∠ABD=20°,
∴∠CDN=∠ADM=60°,
∵MN垂直平分BC,
∴DC=DB,MN⊥BC,
∴∠BDN=∠CDN=60°,
∴∠BDC=∠BDN+∠CDN=60°+60°=120°,
∴∠A=∠BDC﹣∠ABD=120°﹣20°=100°,
∴∠A的度数为100°.
27.如图1,在△ABC中.∠ABC=60°,D,E分别是边AB,BC上的动点,连接AE,CD,且AE,CD交于点F.
(1)若AE,CD为△ABC的角平分线.
①求∠AFC的度数.
②求证:AC=AD+CE.
(2)如图2.若AD=CE,∠ACD=∠CAE,求∠AFC的度数.
【解答】(1)①解:∵AE,CD为△ABC的角平分线,
∴;
∵∠ABC=60°,∠ABC+∠BAC+∠BCA=180°,
∴∠BAC+∠BCA=120°,
∴,
∴∠AFC=180°﹣(∠CAF+∠ACF)=120°;
②证明:如图1,在AC上截取AG=AD,连接FG;
∵∠CAF=∠BAF,AF=AF,
∴△DAF≌△GAF(SAS),
∴∠AFD=∠AFG;
∵∠AFD=180°﹣∠AFC=60°,∠AFC=120°,
∴∠AFG=∠AFD=60°,∠CFG=120°﹣∠AFG=60°=∠CFE,
∵CF=CF,∠ACF=∠ECF,
∴△CFE≌△CFG(ASA),
∴CE=CG,
∴AC=AG+CG=AD+CE;
(2)解:如图2,在FE上截取FH=FD,连接CH;
∵∠ACD=∠CAE,
∴AF=CF,
∵∠AFD=∠CFH,FD=FH,
∴△AFD≌△CFH(SAS),
∴∠FAD=∠FCH,AD=CH;
∵AD=CE,
∴CH=CE,
∴∠CEH=∠CHE;
∵∠CHE=∠CFE+∠FCH,∠CEH=∠B+∠FAD,
∴∠CFE=∠B=60°,
∴∠AFC=180°﹣∠CFE=120°.
一、选择题(本大题共15小题,每小题2分,共30分.在每小题给出的四个选项中,只有一项将合题目要求)
1.(2分)在数学活动课中,同学们利用几何画板绘制出了下列曲线,其中不是轴对称图形的是( )
A.等角螺旋线 B.心形线
C.四叶玫瑰线 D.蝴蝶曲线
2.(2分)以下列各组线段为边,其中能组成三角形的是( )
A.2,2,4 B.4,6,11 C.2,3,8 D.3,5,6
3.(2分)如图所示,△ABC中AC边上的高线是( )
A.线段HA B.线段BH C.线段BC D.线段BA
4.(2分)若直角三角形的一个锐角等于40°,则它的另一个锐角等于( )
A.50° B.60° C.70° D.140°
5.(2分)如图,在△ABC中,∠A=55°,∠B=45°,那么∠ACD的度数为( )
A.110 B.100 C.55 D.45
6.(2分)如图,图中三角形的个数为( )
A.3个 B.4个 C.5个 D.6个
7.(2分)在平面直角坐标系中,点P(2,1)关于y轴对称的点的坐标为( )
A.(2,﹣1) B.(﹣2,1) C.(﹣2,﹣1) D.(1,2)
8.(2分)如图,在△ABC中,AB=AC,D是边BC的中点,若∠BAC=80°,则∠ABC的度数为( )
A.23° B.20° C.50° D.100°
9.(2分)下列说法正确的是( )
A.直角三角形只有一条高
B.多边形的边数越多,其外角和就越大
C.三角形的三条中线都在三角形内部,且交于一点
D.三角形越大,它的内角和就越大
10.(2分)如图,△ABC与△A′B′C′关于直线l对称,若∠A=65°,∠C′=38°,则∠B的度数为( )
A.77° B.38° C.74° D.68°
11.(2分)如图,∠α的度数为( )
A.30° B.40° C.50° D.60°
12.(2分)如图,要测量河两岸相对的两点A,B的距离,可在河的一侧取AB的垂线BM上两点C,D,使BC=CD,再画出BM的垂线DE,使E在AC的延长线上,若BD=10m,DE=12m,CE=13m,则A,B两点的距离是( )
A.5m B.10m C.12m D.13m
13.(2分)△ABC为等腰三角形,AB=AC,∠A=40°,则∠B的度数是( )
A.60° B.70° C.80° D.90°
14.(2分)如图,已知△ABC中,点D、E分别是边BC、AB的中点.若△ABC的面积等于8,则△BDE的面积等于( )
A.2 B.3 C.4 D.5
15.(2分)如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=40°,∠2=25°,则∠B的度数为( )
A.25° B.35° C.45° D.55°
二、填空题(本大题共4小题,每小题2分,共8分)
16.(2分)如图,人字梯中间一般会设计一“拉杆”,以增加使用梯子时的安全性,这样做蕴含的道理是 .
17.(2分)一个多边形从一个顶点出发,可作4条对角线,则这个多边形是 边形.
18.(2分)如图,四边形ABCD≌四边形A′B′C′D′,若∠B=90°,∠C=65°,∠D′=105°,则∠A′=
19.(2分)如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于D,若BD=2CD,点D到边AB的距离为6,则BC的长是 .
三、解答题(本大题共8小题,共62分.解答应写出文字说明、证明过程或演算步骤)
20.已知a、b、c是△ABC的三边长,化简|a+b﹣c|﹣|b﹣a﹣c|.
21.如图,AB=ED,BC=DF,AE=CF且A,E,C,F四点共线,求证:△ABC≌△EDF.
22.如图,在边长为1个单位长度的正方形网格中,建立平面直角坐标系,△ABC是格点三角形(顶点都在网格线交点上的三角形).
(1)作出△ABC关于x轴对称的△A1B1C1.
(2)若在△ABC内有一点P(x,y),则在△A1B1C1内点P的对应点P1的坐标为 .
23.已知一个多边形内角和与外角和之比为11:2.
(1)求这个多边形的内角和;
(2)求这个多边形的边数.
24.如图,△ABC全等于△DEB,E在边AB上,DE与AC交于点F.若DE=10,BC=4,∠D=30°,∠DBA=70°.
(1)求线段AE的长.
(2)求∠DBC的度数.
25.如图,CD,CE分别是∠ABC的高和中线,若AC=3,AB=5,BC=4,∠ACB=90°.
(1)求CD的长.
(2)求△EBC与△ACE的周长之差.
26.如图,在△ABC中,边BC的垂直平分线MN,交边AC于点D,交边BC于点E,连接BD.
(1)若CE=4,△ABD的周长为10,求△ABC的周长.
(2)若∠ADM=60°,∠ABD=20°,求∠A的度数.
27.如图1,在△ABC中.∠ABC=60°,D,E分别是边AB,BC上的动点,连接AE,CD,且AE,CD交于点F.
(1)若AE,CD为△ABC的角平分线.
①求∠AFC的度数.
②求证:AC=AD+CE.
(2)如图2.若AD=CE,∠ACD=∠CAE,求∠AFC的度数.
2024-2025学年云南省昆明八中八年级(上)期中数学试卷
参考答案
一、选择题(本大题共15小题,每小题2分,共30分.在每小题给出的四个选项中,只有一项将合题目要求)
1.(2分)在数学活动课中,同学们利用几何画板绘制出了下列曲线,其中不是轴对称图形的是( )
A.等角螺旋线 B.心形线
C.四叶玫瑰线 D.蝴蝶曲线
选:A.
2.(2分)以下列各组线段为边,其中能组成三角形的是( )
A.2,2,4 B.4,6,11 C.2,3,8 D.3,5,6
选:D.
3.(2分)如图所示,△ABC中AC边上的高线是( )
A.线段HA B.线段BH C.线段BC D.线段BA
选:B.
4.(2分)若直角三角形的一个锐角等于40°,则它的另一个锐角等于( )
A.50° B.60° C.70° D.140°
选:A.
5.(2分)如图,在△ABC中,∠A=55°,∠B=45°,那么∠ACD的度数为( )
A.110 B.100 C.55 D.45
选:B.
6.(2分)如图,图中三角形的个数为( )
A.3个 B.4个 C.5个 D.6个
选:C.
7.(2分)在平面直角坐标系中,点P(2,1)关于y轴对称的点的坐标为( )
A.(2,﹣1) B.(﹣2,1) C.(﹣2,﹣1) D.(1,2)
选:B.
8.(2分)如图,在△ABC中,AB=AC,D是边BC的中点,若∠BAC=80°,则∠ABC的度数为( )
A.23° B.20° C.50° D.100°
选:C.
9.(2分)下列说法正确的是( )
A.直角三角形只有一条高
B.多边形的边数越多,其外角和就越大
C.三角形的三条中线都在三角形内部,且交于一点
D.三角形越大,它的内角和就越大
选:C.
10.(2分)如图,△ABC与△A′B′C′关于直线l对称,若∠A=65°,∠C′=38°,则∠B的度数为( )
A.77° B.38° C.74° D.68°
选:A.
11.(2分)如图,∠α的度数为( )
A.30° B.40° C.50° D.60°
选:B.
12.(2分)如图,要测量河两岸相对的两点A,B的距离,可在河的一侧取AB的垂线BM上两点C,D,使BC=CD,再画出BM的垂线DE,使E在AC的延长线上,若BD=10m,DE=12m,CE=13m,则A,B两点的距离是( )
A.5m B.10m C.12m D.13m
选:C.
13.(2分)△ABC为等腰三角形,AB=AC,∠A=40°,则∠B的度数是( )
A.60° B.70° C.80° D.90°
选:B.
14.(2分)如图,已知△ABC中,点D、E分别是边BC、AB的中点.若△ABC的面积等于8,则△BDE的面积等于( )
A.2 B.3 C.4 D.5
选:A.
15.(2分)如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=40°,∠2=25°,则∠B的度数为( )
A.25° B.35° C.45° D.55°
选:B.
二、填空题(本大题共4小题,每小题2分,共8分)
16.(2分)如图,人字梯中间一般会设计一“拉杆”,以增加使用梯子时的安全性,这样做蕴含的道理是 三角形的稳定性 .
17.(2分)一个多边形从一个顶点出发,可作4条对角线,则这个多边形是 7 边形.
18.(2分)如图,四边形ABCD≌四边形A′B′C′D′,若∠B=90°,∠C=65°,∠D′=105°,则∠A′= 100°
19.(2分)如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于D,若BD=2CD,点D到边AB的距离为6,则BC的长是 18 .
三、解答题(本大题共8小题,共62分.解答应写出文字说明、证明过程或演算步骤)
20.已知a、b、c是△ABC的三边长,化简|a+b﹣c|﹣|b﹣a﹣c|.
【解答】解:∵a、b、c为△ABC的三条边长,
∴a+b﹣c>0,b﹣a﹣c<0,
|a+b﹣c|﹣|b﹣a﹣c|
=a+b﹣c﹣c﹣a+b
=2b﹣2c.
故答案为:2b﹣2c.
21.如图,AB=ED,BC=DF,AE=CF且A,E,C,F四点共线,求证:△ABC≌△EDF.
【解答】证明:∵AE=CF,
∴AE+EC=CF+EC,即AC=EF,
在△ABC和△EDF中,
,
∴△ABC≌△EDF(SSS).
22.如图,在边长为1个单位长度的正方形网格中,建立平面直角坐标系,△ABC是格点三角形(顶点都在网格线交点上的三角形).
(1)作出△ABC关于x轴对称的△A1B1C1.
(2)若在△ABC内有一点P(x,y),则在△A1B1C1内点P的对应点P1的坐标为 (x,﹣y) .
【解答】解:(1)如图,△A1B1C1即为所作.
(2)∵△ABC与△A1B1C1关于x轴对称,点P(x,y)是△ABC内一点,
∴在△A1B1C1内点P的对应点P1的坐标为(x,﹣y),
故答案为:(x,﹣y).
23.已知一个多边形内角和与外角和之比为11:2.
(1)求这个多边形的内角和;
(2)求这个多边形的边数.
【解答】解:(1)360°×=1980°,
答:这个多边形的内角和为1980°;
(2)设该多边形的边数为n
则(n﹣2)×180=360×
解得:n=13.
答:这个多边形的边数为13.
24.如图,△ABC全等于△DEB,E在边AB上,DE与AC交于点F.若DE=10,BC=4,∠D=30°,∠DBA=70°.
(1)求线段AE的长.
(2)求∠DBC的度数.
【解答】解:(1)∵DE=10,BC=4,
∴DE≠BC,
如图所示,BE为△DBE中的最短边,BC为△ABC中的最短边,
∵∠ABC>∠DBE,
∴DE和AC不可能是全等三角形的对应边,
∵E在边AB上,
∴AB≠BE,
∵△ABC全等于△DEB,
∴△ABC≌△DEB,
∴AB=DE=10,BE=BC=4,
∴AE=AB﹣BE=6;
(2)∵△ABC≌△DEB,∠D=30°,∠DBA=70°,
∴∠BAC=∠D=30°,∠DBA=∠C=70°,
∴∠ABC=180°﹣30°﹣70°=80°,
∴∠DBC=∠ABC﹣∠DBE=10°.
25.如图,CD,CE分别是∠ABC的高和中线,若AC=3,AB=5,BC=4,∠ACB=90°.
(1)求CD的长.
(2)求△EBC与△ACE的周长之差.
【解答】解:(1)∵,
∴;
(2)∵∠ABC的中线是CE,
∴AE=BE;
∴△EBC与△ACE的周长之差为:
BE+CE+BC﹣(AC+CE+AE)=BC﹣AC=4﹣3=1.
26.如图,在△ABC中,边BC的垂直平分线MN,交边AC于点D,交边BC于点E,连接BD.
(1)若CE=4,△ABD的周长为10,求△ABC的周长.
(2)若∠ADM=60°,∠ABD=20°,求∠A的度数.
【解答】解:(1)∵MN垂直平分BC,CE=4,
∴DC=DB,BE=CE=4,
∴BC=BE+CE=4+4=8,
∵△ABD的周长为10,
∴10=AB+AD+DB=AB+AD+DC=AB+AC,
∴AB+AC+BC=10+8=18,
∴△ABC的周长为18;
(2)∵∠ADM=60°,∠ABD=20°,
∴∠CDN=∠ADM=60°,
∵MN垂直平分BC,
∴DC=DB,MN⊥BC,
∴∠BDN=∠CDN=60°,
∴∠BDC=∠BDN+∠CDN=60°+60°=120°,
∴∠A=∠BDC﹣∠ABD=120°﹣20°=100°,
∴∠A的度数为100°.
27.如图1,在△ABC中.∠ABC=60°,D,E分别是边AB,BC上的动点,连接AE,CD,且AE,CD交于点F.
(1)若AE,CD为△ABC的角平分线.
①求∠AFC的度数.
②求证:AC=AD+CE.
(2)如图2.若AD=CE,∠ACD=∠CAE,求∠AFC的度数.
【解答】(1)①解:∵AE,CD为△ABC的角平分线,
∴;
∵∠ABC=60°,∠ABC+∠BAC+∠BCA=180°,
∴∠BAC+∠BCA=120°,
∴,
∴∠AFC=180°﹣(∠CAF+∠ACF)=120°;
②证明:如图1,在AC上截取AG=AD,连接FG;
∵∠CAF=∠BAF,AF=AF,
∴△DAF≌△GAF(SAS),
∴∠AFD=∠AFG;
∵∠AFD=180°﹣∠AFC=60°,∠AFC=120°,
∴∠AFG=∠AFD=60°,∠CFG=120°﹣∠AFG=60°=∠CFE,
∵CF=CF,∠ACF=∠ECF,
∴△CFE≌△CFG(ASA),
∴CE=CG,
∴AC=AG+CG=AD+CE;
(2)解:如图2,在FE上截取FH=FD,连接CH;
∵∠ACD=∠CAE,
∴AF=CF,
∵∠AFD=∠CFH,FD=FH,
∴△AFD≌△CFH(SAS),
∴∠FAD=∠FCH,AD=CH;
∵AD=CE,
∴CH=CE,
∴∠CEH=∠CHE;
∵∠CHE=∠CFE+∠FCH,∠CEH=∠B+∠FAD,
∴∠CFE=∠B=60°,
∴∠AFC=180°﹣∠CFE=120°.
同课章节目录
