2024-2025学年浙江省温州市鹿城区九年级(上)期中数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年浙江省温州市鹿城区九年级(上)期中数学试卷(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 478.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-26 00:00:00 | ||
图片预览



文档简介
2024-2025学年浙江省温州市鹿城区九年级(上)期中数学试卷
一、选择题(本题有10小题,每小题3分,共30分)
1.(3分)下列函数中,是二次函数的是( )
A.y=2x B.y= C.y=x2+1 D.y=3x﹣2
2.(3分)下列事件中,属于不确定(随机)事件的是( )
A.掷一次骰子,朝上一面的点数大于0
B.从装有3个白球的袋子中摸出一个红球
C.明天太阳从东方升起
D.奥运射击冠军盛李豪射击一次,命中10环
3.(3分)已知⊙O的半径是5,点P到圆心O的距离是7,则点P在( )
A.圆内 B.圆上 C.圆外 D.不能确定
4.(3分)将抛物线y=x2向右平移1个单位,再向上平移2个单位,所得的新抛物线的表达式为( )
A.y=(x+1)2+2 B.y=(x+2)2+1
C.y=(x+2)2﹣1 D.y=(x﹣1)2+2
5.(3分)书架上一共有3本书,分别是1本数学书,2本科学书.从中任取1本书,取到数学书的概率为( )
A. B. C. D.
6.(3分)如图,在O中,OA,OB为半径,点C为O上一点,若∠ACB=40°,则∠AOB的度数是( )
A.40° B.60° C.80° D.120°
7.(3分)已知点A(2,y1),B(﹣1,y2),C(3,y3)都在抛物线y=x2+x+2 上,则( )
A.y2<y1<y3 B.y3<y1<y2 C.y1<y2<y3 D.y3<y2<y1
8.(3分)小明在一次用频率估计概率的试验中统计了某一结果出现的频率,绘制统计图如图所示,则符合这一结果的实验可能是( )
A.掷一枚正六面体的骰子,出现4点的概率
B.抛一枚硬币,出现反面的概率
C.任意写一个正整数,它能被3整除的概率
D.从一副扑克牌中任抽一张牌,取到“大王”的概率
9.(3分)如图,点A的坐标是(﹣4,6),将线段OA绕点O顺时针旋转90°,点A的对应点的坐标是( )
A.(4,6) B.(6,4) C.(﹣6,﹣4) D.(﹣4,﹣6)
10.(3分)已知二次函数y=x2﹣2x﹣8图象上有两点:点A(xA,yA),B(xB,yB),其中﹣4≤xA≤t,t≤xB≤5.当yA≥yB时,则t的取值范围为( )
A.﹣4≤t≤5 B.﹣4≤t≤﹣1 C.﹣4≤t≤﹣2 D.﹣4≤t≤﹣3
二、填空题(本题有8小题,每小题3分,共24分)
11.(3分)当x=1时,二次函数y=x2﹣7的函数值为 .
12.(3分)某路口红绿灯的时间设置为:红灯40秒,绿灯60秒,黄灯4秒,当车辆随意经过该路口时,遇到可能性最小的是 灯.(填“红、绿、黄”)
13.(3分)如图,已知O的弦AB的长为8,弦AB的弦心距OC的长为3,则O半径的长为 .
14.(3分)在同样条件下对某种小麦种子进行发芽试验,统计发芽种子数,获得如下频数表:
试验种子数(粒) 100 200 500 1000 2000 4000 10000
发芽频数 92 188 476 951 1900 3800 9500
估计该麦芽的发芽概率是 .(精确到0.01)
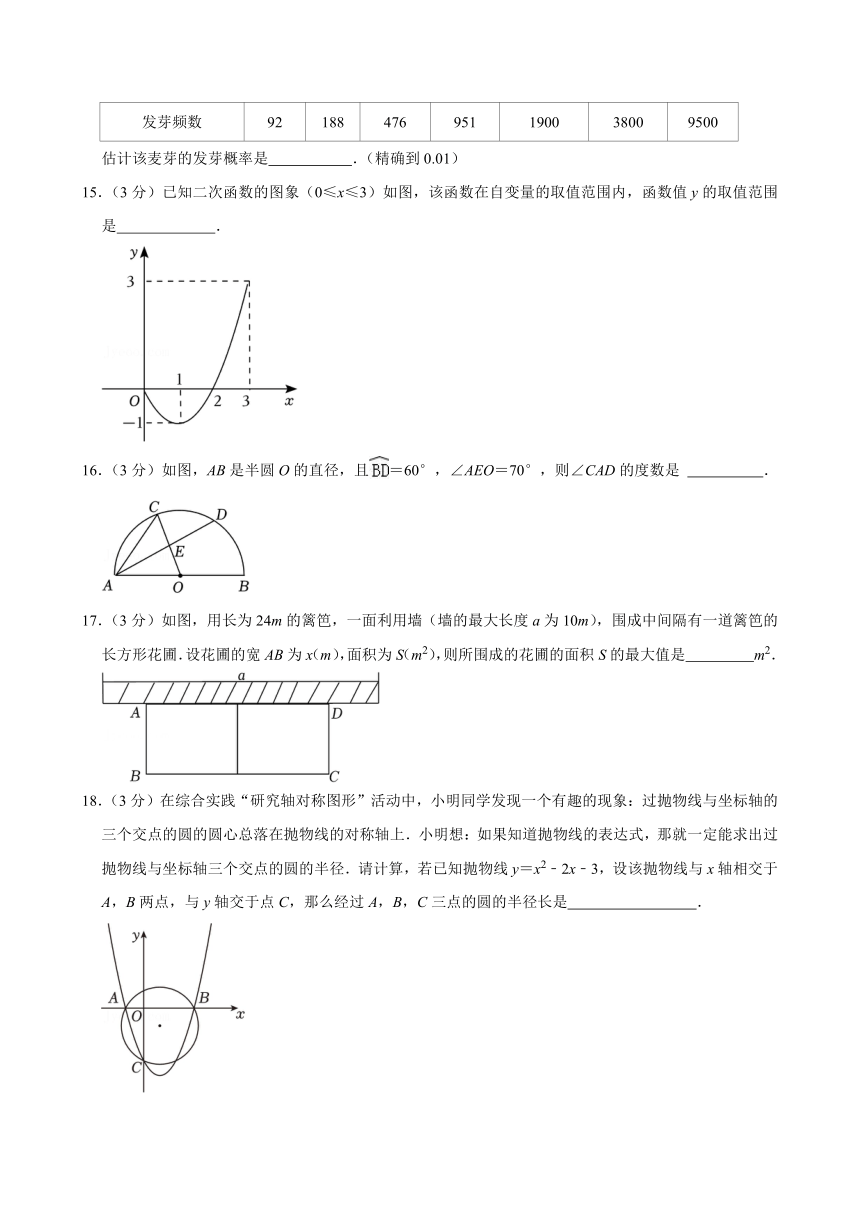
15.(3分)已知二次函数的图象(0≤x≤3)如图,该函数在自变量的取值范围内,函数值y的取值范围是 .
16.(3分)如图,AB是半圆O的直径,且=60°,∠AEO=70°,则∠CAD的度数是 .
17.(3分)如图,用长为24m的篱笆,一面利用墙(墙的最大长度a为10m),围成中间隔有一道篱笆的长方形花圃.设花圃的宽AB为x(m),面积为S(m2),则所围成的花圃的面积S的最大值是 m2.
18.(3分)在综合实践“研究轴对称图形”活动中,小明同学发现一个有趣的现象:过抛物线与坐标轴的三个交点的圆的圆心总落在抛物线的对称轴上.小明想:如果知道抛物线的表达式,那就一定能求出过抛物线与坐标轴三个交点的圆的半径.请计算,若已知抛物线y=x2﹣2x﹣3,设该抛物线与x轴相交于A,B两点,与y轴交于点C,那么经过A,B,C三点的圆的半径长是 .
三、解答题(本题有6小题,共46分)
19.(6分)小S同学积极参加社区志愿者服务工作.在某次活动中,根据社区的安排,志愿者会被随机分到A组(场地布置),B组(场地安保),C组(场地应急).
(1)小S同学被分到B组的概率是 .
(2)小Y同学也参加了本次志愿者服务工作,请用列表或树状图法表示出两人分组的所有可能结果,并求出小Y和小S两位同学被分到同组的概率.
20.(6分)已知二次函数y=x2﹣2x+c,经过点(0,﹣3).
(1)求这个二次函数的表达式.
(2)若点B(1,m)在该函数图象上,求m的值.
22.(6分)如图,AB是⊙O的直径,点C,D是⊙O上的点,且OD∥BC,AC分别与BD,OD相交于点E,F.
(1)求证:点D为的中点.
(2)若DF=8,AC=24,求⊙O的半径长度.
23.(9分)国庆期间某旅游点一家商铺销售一批成本为每件50元的商品,规定销售单价不低于成本价,又不高于每件70元,销售量y(件)与销售单价x(元)的关系可以近似的看作一次函数(如图).
(1)请直接写出y关于x的函数表达式 .
(2)设该商铺销售这批商品获得的总利润(总利润=总销售额﹣总成本)为w元,当销售单价为多少元时,可获得的总利润最大?最大总利润是多少?
(3)若该商铺要保证销售这批商品的利润不能低于4000元,则销售单价x(元)的取值范围是 .(直接写答案)
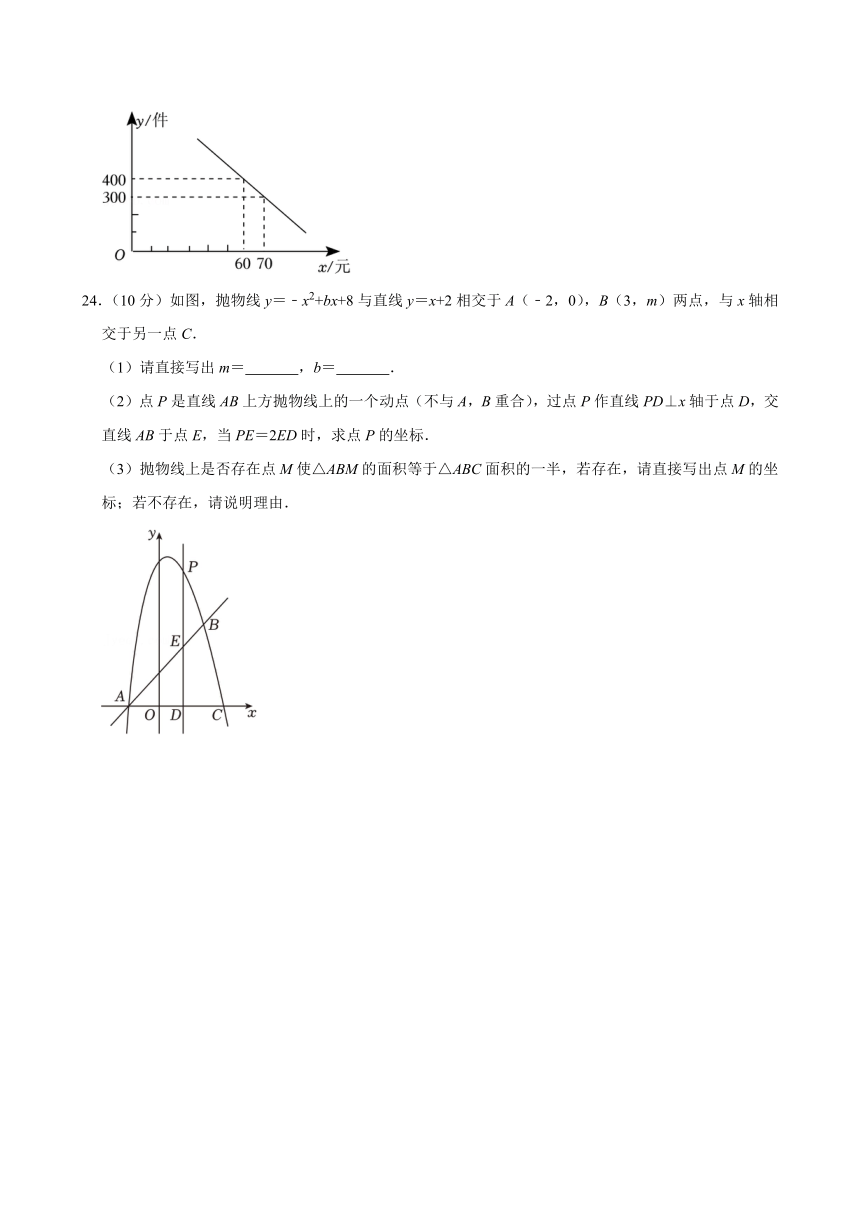
24.(10分)如图,抛物线y=﹣x2+bx+8与直线y=x+2相交于A(﹣2,0),B(3,m)两点,与x轴相交于另一点C.
(1)请直接写出m= ,b= .
(2)点P是直线AB上方抛物线上的一个动点(不与A,B重合),过点P作直线PD⊥x轴于点D,交直线AB于点E,当PE=2ED时,求点P的坐标.
(3)抛物线上是否存在点M使△ABM的面积等于△ABC面积的一半,若存在,请直接写出点M的坐标;若不存在,请说明理由.
2024-2025学年浙江省温州市鹿城区九年级(上)期中数学试卷
参考答案
一、选择题(本题有10小题,每小题3分,共30分)
1.(3分)下列函数中,是二次函数的是( )
A.y=2x B.y= C.y=x2+1 D.y=3x﹣2
选:C.
2.(3分)下列事件中,属于不确定(随机)事件的是( )
A.掷一次骰子,朝上一面的点数大于0
B.从装有3个白球的袋子中摸出一个红球
C.明天太阳从东方升起
D.奥运射击冠军盛李豪射击一次,命中10环
选:D.
3.(3分)已知⊙O的半径是5,点P到圆心O的距离是7,则点P在( )
A.圆内 B.圆上 C.圆外 D.不能确定
选:C.
4.(3分)将抛物线y=x2向右平移1个单位,再向上平移2个单位,所得的新抛物线的表达式为( )
A.y=(x+1)2+2 B.y=(x+2)2+1
C.y=(x+2)2﹣1 D.y=(x﹣1)2+2
选:D.
5.(3分)书架上一共有3本书,分别是1本数学书,2本科学书.从中任取1本书,取到数学书的概率为( )
A. B. C. D.
选:B.
6.(3分)如图,在O中,OA,OB为半径,点C为O上一点,若∠ACB=40°,则∠AOB的度数是( )
A.40° B.60° C.80° D.120°
选:C.
7.(3分)已知点A(2,y1),B(﹣1,y2),C(3,y3)都在抛物线y=x2+x+2 上,则( )
A.y2<y1<y3 B.y3<y1<y2 C.y1<y2<y3 D.y3<y2<y1
选:A.
8.(3分)小明在一次用频率估计概率的试验中统计了某一结果出现的频率,绘制统计图如图所示,则符合这一结果的实验可能是( )
A.掷一枚正六面体的骰子,出现4点的概率
B.抛一枚硬币,出现反面的概率
C.任意写一个正整数,它能被3整除的概率
D.从一副扑克牌中任抽一张牌,取到“大王”的概率
选:C.
9.(3分)如图,点A的坐标是(﹣4,6),将线段OA绕点O顺时针旋转90°,点A的对应点的坐标是( )
A.(4,6) B.(6,4) C.(﹣6,﹣4) D.(﹣4,﹣6)
选:B.
10.(3分)已知二次函数y=x2﹣2x﹣8图象上有两点:点A(xA,yA),B(xB,yB),其中﹣4≤xA≤t,t≤xB≤5.当yA≥yB时,则t的取值范围为( )
A.﹣4≤t≤5 B.﹣4≤t≤﹣1 C.﹣4≤t≤﹣2 D.﹣4≤t≤﹣3
选:D.
二、填空题(本题有8小题,每小题3分,共24分)
11.(3分)当x=1时,二次函数y=x2﹣7的函数值为 ﹣6 .
12.(3分)某路口红绿灯的时间设置为:红灯40秒,绿灯60秒,黄灯4秒,当车辆随意经过该路口时,遇到可能性最小的是 黄 灯.(填“红、绿、黄”)
13.(3分)如图,已知O的弦AB的长为8,弦AB的弦心距OC的长为3,则O半径的长为 5 .
14.(3分)在同样条件下对某种小麦种子进行发芽试验,统计发芽种子数,获得如下频数表:
试验种子数(粒) 100 200 500 1000 2000 4000 10000
发芽频数 92 188 476 951 1900 3800 9500
估计该麦芽的发芽概率是 0.95 .(精确到0.01)
15.(3分)已知二次函数的图象(0≤x≤3)如图,该函数在自变量的取值范围内,函数值y的取值范围是 ﹣1≤y≤3 .
16.(3分)如图,AB是半圆O的直径,且=60°,∠AEO=70°,则∠CAD的度数是 20° .
17.(3分)如图,用长为24m的篱笆,一面利用墙(墙的最大长度a为10m),围成中间隔有一道篱笆的长方形花圃.设花圃的宽AB为x(m),面积为S(m2),则所围成的花圃的面积S的最大值是 48 m2.
18.(3分)在综合实践“研究轴对称图形”活动中,小明同学发现一个有趣的现象:过抛物线与坐标轴的三个交点的圆的圆心总落在抛物线的对称轴上.小明想:如果知道抛物线的表达式,那就一定能求出过抛物线与坐标轴三个交点的圆的半径.请计算,若已知抛物线y=x2﹣2x﹣3,设该抛物线与x轴相交于A,B两点,与y轴交于点C,那么经过A,B,C三点的圆的半径长是 .
三、解答题(本题有6小题,共46分)
19.(6分)小S同学积极参加社区志愿者服务工作.在某次活动中,根据社区的安排,志愿者会被随机分到A组(场地布置),B组(场地安保),C组(场地应急).
(1)小S同学被分到B组的概率是 .
(2)小Y同学也参加了本次志愿者服务工作,请用列表或树状图法表示出两人分组的所有可能结果,并求出小Y和小S两位同学被分到同组的概率.
【解答】解:(1)由题意知,共有3种等可能的结果,其中小S同学被分到B组的结果有1种,
∴小S同学被分到B组的概率是.
故答案为:.
(2)列表如下:
A B C
A (A,A) (A,B) (A,C)
B (B,A) (B,B) (B,C)
C (C,A) (C,B) (C,C)
由表格可知,两人分组的所有等可能的结果共有9种,
其中小Y和小S两位同学被分到同组的结果有3种,
∴小Y和小S两位同学被分到同组的概率为.
20.(6分)已知二次函数y=x2﹣2x+c,经过点(0,﹣3).
(1)求这个二次函数的表达式.
(2)若点B(1,m)在该函数图象上,求m的值.
【解答】解:(1)将点(0,﹣3)代入二次函数y=x2﹣2x+c得:
c=﹣3,
∴二次函数解析式为:y=x2﹣2x﹣3.
(2)将点B(1,m)坐标代入y=x2﹣2x﹣3得:
1﹣2﹣3=m,
解得:m=﹣4.
22.(6分)如图,AB是⊙O的直径,点C,D是⊙O上的点,且OD∥BC,AC分别与BD,OD相交于点E,F.
(1)求证:点D为的中点.
(2)若DF=8,AC=24,求⊙O的半径长度.
【解答】(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∵OD∥BC,
∴∠OFA=90°,
∴OF⊥AC,
∴=,
即点D为的中点;
(2)解:OF⊥AC,
∴AF=AC=12,
∵DF=8,
∴OF=OD﹣DF=OA﹣8,
∵OA2=AF2+OF2,
∴OA2=122+(OA﹣8)2,
∴OA=13,
∴⊙O的半径为13.
23.(9分)国庆期间某旅游点一家商铺销售一批成本为每件50元的商品,规定销售单价不低于成本价,又不高于每件70元,销售量y(件)与销售单价x(元)的关系可以近似的看作一次函数(如图).
(1)请直接写出y关于x的函数表达式 y=﹣10x+1000 .
(2)设该商铺销售这批商品获得的总利润(总利润=总销售额﹣总成本)为w元,当销售单价为多少元时,可获得的总利润最大?最大总利润是多少?
(3)若该商铺要保证销售这批商品的利润不能低于4000元,则销售单价x(元)的取值范围是 60≤x≤70 .(直接写答案)
【解答】解:(1)设y与x的函数关系式为:y=kx+b,
∵函数图象经过点(60,400)和(70,300),
∴,
解得:.
故y与x之间的函数关系式为:y=﹣10x+1000;
故答案为:y=﹣10x+1000;
(2)由题意可得出:
w=(x﹣50)(﹣10x+1000)
=﹣10x2+1500x﹣50000,
自变量取值范围:50≤x≤70.
∵﹣,a=﹣10<0.
∴函数w=﹣10x2+1500x﹣50000图象开口向下,对称轴是直线x=75.
∵50≤x≤70,此时y随x的增大而增大,
∴当x=70时,P最大值=6000;
故当销售单价为70元时,可获得的总利润最大;最大总利润是6000元;
(3)由w≥4000,
当w=4000时,4000=﹣10x2+1500x﹣50000,
解得:x1=60,x2=90,
∵a=﹣10<0,
∴60≤x≤90,
又∵50≤x≤70;
∴60≤x≤70,
故答案为:60≤x≤70.
24.(10分)如图,抛物线y=﹣x2+bx+8与直线y=x+2相交于A(﹣2,0),B(3,m)两点,与x轴相交于另一点C.
(1)请直接写出m= 5 ,b= 2 .
(2)点P是直线AB上方抛物线上的一个动点(不与A,B重合),过点P作直线PD⊥x轴于点D,交直线AB于点E,当PE=2ED时,求点P的坐标.
(3)抛物线上是否存在点M使△ABM的面积等于△ABC面积的一半,若存在,请直接写出点M的坐标;若不存在,请说明理由.
【解答】解:(1)把B(3,m)代入y=x+2得:m=3+2=5,
把A(﹣2,0)代入y=﹣x2+bx+8得:
﹣4﹣2b+8=0,
解得:b=2,
故答案为:5;2;
(2)由(1)知抛物线的解析式为y=﹣x2+2x+8,设P(t,﹣t2+2t+8),则E(t,t+2),D(t,0),
∵PE=2DE,
∴﹣t2+2t+8﹣(t+2)=2(t+2),
解得t=1或t=﹣2(此时P不在直线AB上方,舍去);
∴P的坐标为(1,9);
(3)抛物线上存在点M,使△ABM的面积等于△ABC面积的一半;理由如下:
过M作MK∥y轴交直线AB于K,过点B作BE⊥MK,延长MK交x轴于点F,如图:
在y=﹣x2+2x+8中,令y=0得0=﹣x2+2x+8,
解得x=﹣2或x=4,
∴A(﹣2,0),C(4,0),
∴AC=6,
∵B(3,5),
∴,
设M(m,﹣m2+2m+8),则K(m,m+2),
∴MK=|﹣m2+2m+8﹣(m+2)|=|﹣m2+m+6|,
∵,
∴,
∵△ABM的面积等于△ABC面积的一半,
∴,
∴|﹣m2+m+6|=3,
∴﹣m2+m+6=3或﹣m2+m+6=﹣3,
解得或,
解得或
∴M的坐标为或或或,.
一、选择题(本题有10小题,每小题3分,共30分)
1.(3分)下列函数中,是二次函数的是( )
A.y=2x B.y= C.y=x2+1 D.y=3x﹣2
2.(3分)下列事件中,属于不确定(随机)事件的是( )
A.掷一次骰子,朝上一面的点数大于0
B.从装有3个白球的袋子中摸出一个红球
C.明天太阳从东方升起
D.奥运射击冠军盛李豪射击一次,命中10环
3.(3分)已知⊙O的半径是5,点P到圆心O的距离是7,则点P在( )
A.圆内 B.圆上 C.圆外 D.不能确定
4.(3分)将抛物线y=x2向右平移1个单位,再向上平移2个单位,所得的新抛物线的表达式为( )
A.y=(x+1)2+2 B.y=(x+2)2+1
C.y=(x+2)2﹣1 D.y=(x﹣1)2+2
5.(3分)书架上一共有3本书,分别是1本数学书,2本科学书.从中任取1本书,取到数学书的概率为( )
A. B. C. D.
6.(3分)如图,在O中,OA,OB为半径,点C为O上一点,若∠ACB=40°,则∠AOB的度数是( )
A.40° B.60° C.80° D.120°
7.(3分)已知点A(2,y1),B(﹣1,y2),C(3,y3)都在抛物线y=x2+x+2 上,则( )
A.y2<y1<y3 B.y3<y1<y2 C.y1<y2<y3 D.y3<y2<y1
8.(3分)小明在一次用频率估计概率的试验中统计了某一结果出现的频率,绘制统计图如图所示,则符合这一结果的实验可能是( )
A.掷一枚正六面体的骰子,出现4点的概率
B.抛一枚硬币,出现反面的概率
C.任意写一个正整数,它能被3整除的概率
D.从一副扑克牌中任抽一张牌,取到“大王”的概率
9.(3分)如图,点A的坐标是(﹣4,6),将线段OA绕点O顺时针旋转90°,点A的对应点的坐标是( )
A.(4,6) B.(6,4) C.(﹣6,﹣4) D.(﹣4,﹣6)
10.(3分)已知二次函数y=x2﹣2x﹣8图象上有两点:点A(xA,yA),B(xB,yB),其中﹣4≤xA≤t,t≤xB≤5.当yA≥yB时,则t的取值范围为( )
A.﹣4≤t≤5 B.﹣4≤t≤﹣1 C.﹣4≤t≤﹣2 D.﹣4≤t≤﹣3
二、填空题(本题有8小题,每小题3分,共24分)
11.(3分)当x=1时,二次函数y=x2﹣7的函数值为 .
12.(3分)某路口红绿灯的时间设置为:红灯40秒,绿灯60秒,黄灯4秒,当车辆随意经过该路口时,遇到可能性最小的是 灯.(填“红、绿、黄”)
13.(3分)如图,已知O的弦AB的长为8,弦AB的弦心距OC的长为3,则O半径的长为 .
14.(3分)在同样条件下对某种小麦种子进行发芽试验,统计发芽种子数,获得如下频数表:
试验种子数(粒) 100 200 500 1000 2000 4000 10000
发芽频数 92 188 476 951 1900 3800 9500
估计该麦芽的发芽概率是 .(精确到0.01)
15.(3分)已知二次函数的图象(0≤x≤3)如图,该函数在自变量的取值范围内,函数值y的取值范围是 .
16.(3分)如图,AB是半圆O的直径,且=60°,∠AEO=70°,则∠CAD的度数是 .
17.(3分)如图,用长为24m的篱笆,一面利用墙(墙的最大长度a为10m),围成中间隔有一道篱笆的长方形花圃.设花圃的宽AB为x(m),面积为S(m2),则所围成的花圃的面积S的最大值是 m2.
18.(3分)在综合实践“研究轴对称图形”活动中,小明同学发现一个有趣的现象:过抛物线与坐标轴的三个交点的圆的圆心总落在抛物线的对称轴上.小明想:如果知道抛物线的表达式,那就一定能求出过抛物线与坐标轴三个交点的圆的半径.请计算,若已知抛物线y=x2﹣2x﹣3,设该抛物线与x轴相交于A,B两点,与y轴交于点C,那么经过A,B,C三点的圆的半径长是 .
三、解答题(本题有6小题,共46分)
19.(6分)小S同学积极参加社区志愿者服务工作.在某次活动中,根据社区的安排,志愿者会被随机分到A组(场地布置),B组(场地安保),C组(场地应急).
(1)小S同学被分到B组的概率是 .
(2)小Y同学也参加了本次志愿者服务工作,请用列表或树状图法表示出两人分组的所有可能结果,并求出小Y和小S两位同学被分到同组的概率.
20.(6分)已知二次函数y=x2﹣2x+c,经过点(0,﹣3).
(1)求这个二次函数的表达式.
(2)若点B(1,m)在该函数图象上,求m的值.
22.(6分)如图,AB是⊙O的直径,点C,D是⊙O上的点,且OD∥BC,AC分别与BD,OD相交于点E,F.
(1)求证:点D为的中点.
(2)若DF=8,AC=24,求⊙O的半径长度.
23.(9分)国庆期间某旅游点一家商铺销售一批成本为每件50元的商品,规定销售单价不低于成本价,又不高于每件70元,销售量y(件)与销售单价x(元)的关系可以近似的看作一次函数(如图).
(1)请直接写出y关于x的函数表达式 .
(2)设该商铺销售这批商品获得的总利润(总利润=总销售额﹣总成本)为w元,当销售单价为多少元时,可获得的总利润最大?最大总利润是多少?
(3)若该商铺要保证销售这批商品的利润不能低于4000元,则销售单价x(元)的取值范围是 .(直接写答案)
24.(10分)如图,抛物线y=﹣x2+bx+8与直线y=x+2相交于A(﹣2,0),B(3,m)两点,与x轴相交于另一点C.
(1)请直接写出m= ,b= .
(2)点P是直线AB上方抛物线上的一个动点(不与A,B重合),过点P作直线PD⊥x轴于点D,交直线AB于点E,当PE=2ED时,求点P的坐标.
(3)抛物线上是否存在点M使△ABM的面积等于△ABC面积的一半,若存在,请直接写出点M的坐标;若不存在,请说明理由.
2024-2025学年浙江省温州市鹿城区九年级(上)期中数学试卷
参考答案
一、选择题(本题有10小题,每小题3分,共30分)
1.(3分)下列函数中,是二次函数的是( )
A.y=2x B.y= C.y=x2+1 D.y=3x﹣2
选:C.
2.(3分)下列事件中,属于不确定(随机)事件的是( )
A.掷一次骰子,朝上一面的点数大于0
B.从装有3个白球的袋子中摸出一个红球
C.明天太阳从东方升起
D.奥运射击冠军盛李豪射击一次,命中10环
选:D.
3.(3分)已知⊙O的半径是5,点P到圆心O的距离是7,则点P在( )
A.圆内 B.圆上 C.圆外 D.不能确定
选:C.
4.(3分)将抛物线y=x2向右平移1个单位,再向上平移2个单位,所得的新抛物线的表达式为( )
A.y=(x+1)2+2 B.y=(x+2)2+1
C.y=(x+2)2﹣1 D.y=(x﹣1)2+2
选:D.
5.(3分)书架上一共有3本书,分别是1本数学书,2本科学书.从中任取1本书,取到数学书的概率为( )
A. B. C. D.
选:B.
6.(3分)如图,在O中,OA,OB为半径,点C为O上一点,若∠ACB=40°,则∠AOB的度数是( )
A.40° B.60° C.80° D.120°
选:C.
7.(3分)已知点A(2,y1),B(﹣1,y2),C(3,y3)都在抛物线y=x2+x+2 上,则( )
A.y2<y1<y3 B.y3<y1<y2 C.y1<y2<y3 D.y3<y2<y1
选:A.
8.(3分)小明在一次用频率估计概率的试验中统计了某一结果出现的频率,绘制统计图如图所示,则符合这一结果的实验可能是( )
A.掷一枚正六面体的骰子,出现4点的概率
B.抛一枚硬币,出现反面的概率
C.任意写一个正整数,它能被3整除的概率
D.从一副扑克牌中任抽一张牌,取到“大王”的概率
选:C.
9.(3分)如图,点A的坐标是(﹣4,6),将线段OA绕点O顺时针旋转90°,点A的对应点的坐标是( )
A.(4,6) B.(6,4) C.(﹣6,﹣4) D.(﹣4,﹣6)
选:B.
10.(3分)已知二次函数y=x2﹣2x﹣8图象上有两点:点A(xA,yA),B(xB,yB),其中﹣4≤xA≤t,t≤xB≤5.当yA≥yB时,则t的取值范围为( )
A.﹣4≤t≤5 B.﹣4≤t≤﹣1 C.﹣4≤t≤﹣2 D.﹣4≤t≤﹣3
选:D.
二、填空题(本题有8小题,每小题3分,共24分)
11.(3分)当x=1时,二次函数y=x2﹣7的函数值为 ﹣6 .
12.(3分)某路口红绿灯的时间设置为:红灯40秒,绿灯60秒,黄灯4秒,当车辆随意经过该路口时,遇到可能性最小的是 黄 灯.(填“红、绿、黄”)
13.(3分)如图,已知O的弦AB的长为8,弦AB的弦心距OC的长为3,则O半径的长为 5 .
14.(3分)在同样条件下对某种小麦种子进行发芽试验,统计发芽种子数,获得如下频数表:
试验种子数(粒) 100 200 500 1000 2000 4000 10000
发芽频数 92 188 476 951 1900 3800 9500
估计该麦芽的发芽概率是 0.95 .(精确到0.01)
15.(3分)已知二次函数的图象(0≤x≤3)如图,该函数在自变量的取值范围内,函数值y的取值范围是 ﹣1≤y≤3 .
16.(3分)如图,AB是半圆O的直径,且=60°,∠AEO=70°,则∠CAD的度数是 20° .
17.(3分)如图,用长为24m的篱笆,一面利用墙(墙的最大长度a为10m),围成中间隔有一道篱笆的长方形花圃.设花圃的宽AB为x(m),面积为S(m2),则所围成的花圃的面积S的最大值是 48 m2.
18.(3分)在综合实践“研究轴对称图形”活动中,小明同学发现一个有趣的现象:过抛物线与坐标轴的三个交点的圆的圆心总落在抛物线的对称轴上.小明想:如果知道抛物线的表达式,那就一定能求出过抛物线与坐标轴三个交点的圆的半径.请计算,若已知抛物线y=x2﹣2x﹣3,设该抛物线与x轴相交于A,B两点,与y轴交于点C,那么经过A,B,C三点的圆的半径长是 .
三、解答题(本题有6小题,共46分)
19.(6分)小S同学积极参加社区志愿者服务工作.在某次活动中,根据社区的安排,志愿者会被随机分到A组(场地布置),B组(场地安保),C组(场地应急).
(1)小S同学被分到B组的概率是 .
(2)小Y同学也参加了本次志愿者服务工作,请用列表或树状图法表示出两人分组的所有可能结果,并求出小Y和小S两位同学被分到同组的概率.
【解答】解:(1)由题意知,共有3种等可能的结果,其中小S同学被分到B组的结果有1种,
∴小S同学被分到B组的概率是.
故答案为:.
(2)列表如下:
A B C
A (A,A) (A,B) (A,C)
B (B,A) (B,B) (B,C)
C (C,A) (C,B) (C,C)
由表格可知,两人分组的所有等可能的结果共有9种,
其中小Y和小S两位同学被分到同组的结果有3种,
∴小Y和小S两位同学被分到同组的概率为.
20.(6分)已知二次函数y=x2﹣2x+c,经过点(0,﹣3).
(1)求这个二次函数的表达式.
(2)若点B(1,m)在该函数图象上,求m的值.
【解答】解:(1)将点(0,﹣3)代入二次函数y=x2﹣2x+c得:
c=﹣3,
∴二次函数解析式为:y=x2﹣2x﹣3.
(2)将点B(1,m)坐标代入y=x2﹣2x﹣3得:
1﹣2﹣3=m,
解得:m=﹣4.
22.(6分)如图,AB是⊙O的直径,点C,D是⊙O上的点,且OD∥BC,AC分别与BD,OD相交于点E,F.
(1)求证:点D为的中点.
(2)若DF=8,AC=24,求⊙O的半径长度.
【解答】(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∵OD∥BC,
∴∠OFA=90°,
∴OF⊥AC,
∴=,
即点D为的中点;
(2)解:OF⊥AC,
∴AF=AC=12,
∵DF=8,
∴OF=OD﹣DF=OA﹣8,
∵OA2=AF2+OF2,
∴OA2=122+(OA﹣8)2,
∴OA=13,
∴⊙O的半径为13.
23.(9分)国庆期间某旅游点一家商铺销售一批成本为每件50元的商品,规定销售单价不低于成本价,又不高于每件70元,销售量y(件)与销售单价x(元)的关系可以近似的看作一次函数(如图).
(1)请直接写出y关于x的函数表达式 y=﹣10x+1000 .
(2)设该商铺销售这批商品获得的总利润(总利润=总销售额﹣总成本)为w元,当销售单价为多少元时,可获得的总利润最大?最大总利润是多少?
(3)若该商铺要保证销售这批商品的利润不能低于4000元,则销售单价x(元)的取值范围是 60≤x≤70 .(直接写答案)
【解答】解:(1)设y与x的函数关系式为:y=kx+b,
∵函数图象经过点(60,400)和(70,300),
∴,
解得:.
故y与x之间的函数关系式为:y=﹣10x+1000;
故答案为:y=﹣10x+1000;
(2)由题意可得出:
w=(x﹣50)(﹣10x+1000)
=﹣10x2+1500x﹣50000,
自变量取值范围:50≤x≤70.
∵﹣,a=﹣10<0.
∴函数w=﹣10x2+1500x﹣50000图象开口向下,对称轴是直线x=75.
∵50≤x≤70,此时y随x的增大而增大,
∴当x=70时,P最大值=6000;
故当销售单价为70元时,可获得的总利润最大;最大总利润是6000元;
(3)由w≥4000,
当w=4000时,4000=﹣10x2+1500x﹣50000,
解得:x1=60,x2=90,
∵a=﹣10<0,
∴60≤x≤90,
又∵50≤x≤70;
∴60≤x≤70,
故答案为:60≤x≤70.
24.(10分)如图,抛物线y=﹣x2+bx+8与直线y=x+2相交于A(﹣2,0),B(3,m)两点,与x轴相交于另一点C.
(1)请直接写出m= 5 ,b= 2 .
(2)点P是直线AB上方抛物线上的一个动点(不与A,B重合),过点P作直线PD⊥x轴于点D,交直线AB于点E,当PE=2ED时,求点P的坐标.
(3)抛物线上是否存在点M使△ABM的面积等于△ABC面积的一半,若存在,请直接写出点M的坐标;若不存在,请说明理由.
【解答】解:(1)把B(3,m)代入y=x+2得:m=3+2=5,
把A(﹣2,0)代入y=﹣x2+bx+8得:
﹣4﹣2b+8=0,
解得:b=2,
故答案为:5;2;
(2)由(1)知抛物线的解析式为y=﹣x2+2x+8,设P(t,﹣t2+2t+8),则E(t,t+2),D(t,0),
∵PE=2DE,
∴﹣t2+2t+8﹣(t+2)=2(t+2),
解得t=1或t=﹣2(此时P不在直线AB上方,舍去);
∴P的坐标为(1,9);
(3)抛物线上存在点M,使△ABM的面积等于△ABC面积的一半;理由如下:
过M作MK∥y轴交直线AB于K,过点B作BE⊥MK,延长MK交x轴于点F,如图:
在y=﹣x2+2x+8中,令y=0得0=﹣x2+2x+8,
解得x=﹣2或x=4,
∴A(﹣2,0),C(4,0),
∴AC=6,
∵B(3,5),
∴,
设M(m,﹣m2+2m+8),则K(m,m+2),
∴MK=|﹣m2+2m+8﹣(m+2)|=|﹣m2+m+6|,
∵,
∴,
∵△ABM的面积等于△ABC面积的一半,
∴,
∴|﹣m2+m+6|=3,
∴﹣m2+m+6=3或﹣m2+m+6=﹣3,
解得或,
解得或
∴M的坐标为或或或,.
同课章节目录
