苏科版八年级数学下册第10章 分式 第5节 分式方程
文档属性
| 名称 | 苏科版八年级数学下册第10章 分式 第5节 分式方程 |
|
|
| 格式 | zip | ||
| 文件大小 | 28.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-24 00:00:00 | ||
图片预览



文档简介
分式方程 第一课时
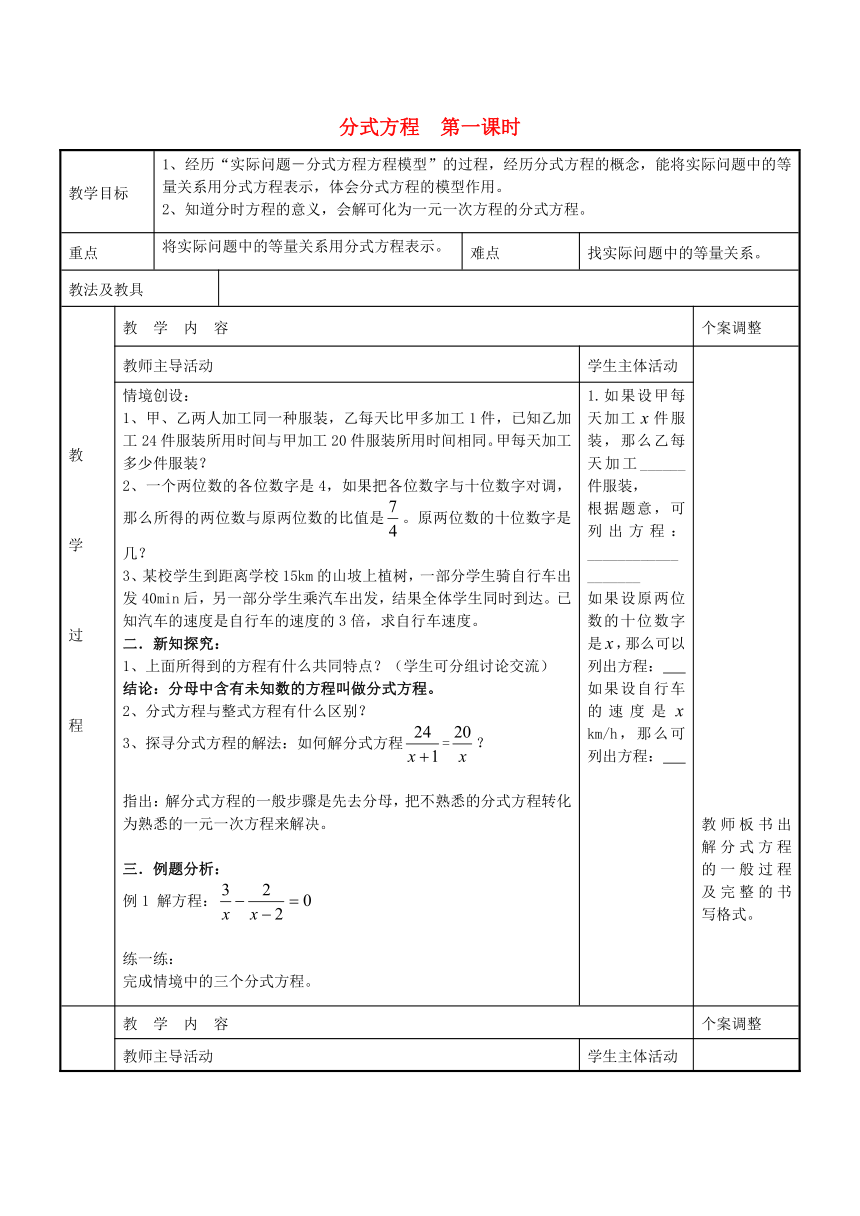
教学目标 1、经历“实际问题-分式方程方程模型”的过程,经历分式方程的概念,能将实际问题中的等量关系用分式方程表示,体会分式方程的模型作用。2、知道分时方程的意义,会解可化为一元一次方程的分式方程。
重点 将实际问题中的等量关系用分式方程表示。 难点 找实际问题中的等量关系。
教法及教具
教学过程 教 学 内 容 个案调整
教师主导活动 学生主体活动 教师板书出解分式方程的一般过程及完整的书写格式。
情境创设:1、甲、乙两人加工同一种服装,乙每天比甲多加工1件,已知乙加工24件服装所用时间与甲加工20件服装所用时间相同。甲每天加工多少件服装?2、一个两位数的各位数字是4,如果把各位数字与十位数字对调,那么所得的两位数与原两位数的比值是。原两位数的十位数字是几?3、某校学生到距离学校15km的山坡上植 ( http: / / www.21cnjy.com )树,一部分学生骑自行车出发40min后,另一部分学生乘汽车出发,结果全体学生同时到达。已知汽车的速度是自行车的速度的3倍,求自行车速度。二.新知探究:1、上面所得到的方程有什么共同特点?(学生可分组讨论交流)结论:分母中含有未知数的方程叫做分式方程。2、分式方程与整式方程有什么区别?3、探寻分式方程的解法:如何解分式方程=?指出:解分式方程的一般步骤是先去分母,把不熟悉的分式方程转化为熟悉的一元一次方程来解决。三.例题分析:例1 解方程:练一练:完成情境中的三个分式方程。 1.如果设甲每天加工件服装,那么乙每天加工______件服装,根据题意,可列出方程:___________________如果设原两位数的十位数字是,那么可以列出方程: 如果设自行车的速度是 km/h,那么可列出方程:
教学过程 教 学 内 容 个案调整
教师主导活动 学生主体活动
例2 从甲地到乙地有两条公路:一条是全长600 km的普通公路,另一条是全长480 km的高速公路。某客车在高速公路上行驶的平均速度比在普通公路上快45 km/h,由高速公路从甲地到乙地所需的时间是由普通公路从甲地到乙地所需时间的一半。求该客车由高速公路从甲地到乙地所需的时间。练习1、轮船在顺水中航行20千米与逆水航行10千米所用时间相同,水流速度为2.5千米/小时,求轮船的静水速度。若分式方程的一个解是,则 。3、解方程: 4.某农场开挖一条480米的渠道,开工后,每天比原计划多挖20米,结果提前4天完成任务,若设原计划每天挖米,那么求时所列方程正确的是( )A、 B、 C、 D、 五.小结
板书设计(用案人完成)
作业布置
教学札记
分式方程 第二课时
教学目标 1、经历探索分式方程解法的过程,会解可化为一元一次方程的分式方程。2、了解分式方程产生增根的原因,会检验根的合理性。
重点 分式方程的解法 难点 解分式方程要验根
教法及教具
教学过程 教 学 内 容 个案调整
教师主导活动 学生主体活动
情境创设:解方程:(1)(2)探索活动:1、方程(1)和方程(2)的求解步骤有差异吗?2、这两个方程有解吗?在这里,x=2是方程(2)的根吗?为什么?3、你认为在解分式方程的过程中,那一步变形可能引起增根? 产生增根的原因是:我们在方程的两边同乘了一个可能使分母为0的整式。因为解分式方程可能产生增根,所以解分式方程必须检验。你能用比较简洁的方法检验解分式方程产生的、想一想解分式方程一般需要经过哪几个步骤?二.例题分析:例1 解下列方程: (1) (2)总结:解分式方程的一般步骤:去分母(注意防止漏乘);去括号(注意先确定符号)有同类项及时的合并同类项;移项;未知数的系数化为1;验根(解分式方程必须要验根)。 2.说明:在这里,x=2不是原方程(2)的根,因为它使得原分式方程的分母为零,我们称它为原方程的增根。
教学过程 教 学 内 容 个案调整
教师主导活动 学生主体活动
课堂练习1、解方程: 2、填空(1)若关于x的方程的解是x=1,则m= ; (2)若方程有增根,则;3、选择(1)下列关于分式方程增根的说法正确的是 ( )A.使所有的分母的值都为零的解是增根 B.分式方程的解为零就是增根C.使分子的值为零的解就是增根 D.使最简公分母的值为零的解是增根(2)方程可能产生的增根是 ( ) A.1 B.2 C.-1或2 D.1或2 四.小结
板书设计(用案人完成)
作业布置
教学札记
分式方程 第三课时
教学目标 1、能将实际问题中的等量关系用分式方程表示,列出分式方程解决简单的实际问题,并能根据实际问题的意义检验所得的结果是否合理。2、发展学生分析问题、解决问题的能力,渗透数学的转化思想人体,培养学生的应用意识。
重点 如何结合实际分析问题,列出分式方程 难点 分析过程,得到等量关系
教法及教具
教学过程 教 学 内 容 个案调整
教师主导活动 学生主体活动
复习巩固:1、解分式方程的一般步骤有哪些?2、解方程:(1)= (2)+=2二.情境创设 甲、乙两地相距19千米,某人从甲地出发出乙地,先步行7千米,然后改骑自行车,共用2小时到达乙地。已知这个人骑自行车的速度是步行速度的4倍。若设这个人步行的速度为千米/小时, ⑴这个人步行时间为 小时,骑车时间为 小时。⑵求步行速度和骑自行车的速度。例题分析例1. 为迎接市中学生田径运动会,计划由某校八年级(1)班的3个小组制作240面彩旗,后因一个小组另有任务,改由另外两个小组完成制作彩旗的任务。这样,这两个小组的每个同学就要比原计划多做4面。如果这3个小组的人数相等,那么每个小组有多少名学生? 学生练习,板演,注意最后验根。先个人思考,再互相交流,尝试从不同角度寻求解决问题的方法,找出题中的等量关系,根据等量关系列出方程。
教学过程 教 学 内 容 个案调整
教师主导活动 学生主体活动
例2、甲、乙两公司各为“见义勇为基金会”捐 ( http: / / www.21cnjy.com )款30000元,已知乙公司比甲公司人均多捐款20元,且甲公司的人数比乙公司的人数多20%。问甲、乙两公司各有多少人?总结:用分式方程解实际问题的一般步骤:设未知数根据题意列方程解方程检验答课堂练习 1.为了帮助遭受自然灾害的地区重建家园,某学校号召同学们自愿捐款。已知第一次捐款总额为4800元,第二次捐款总额为5000元,第二次捐款人数比第一次多20人,而且两次人均捐款额恰好相等。如果设第一次捐款人数为人,那么满足怎样的方程? 2、为改善生态环境,防止水土流失,某村 ( http: / / www.21cnjy.com )拟在荒坡地上种植960棵树, 由于青年团员的支持,每日比原计划多种20棵,结果提前4天完成任务,原计划每天种植多少棵 五.小结
板书设计(用案人完成)
作业布置
教学札记
教学目标 1、经历“实际问题-分式方程方程模型”的过程,经历分式方程的概念,能将实际问题中的等量关系用分式方程表示,体会分式方程的模型作用。2、知道分时方程的意义,会解可化为一元一次方程的分式方程。
重点 将实际问题中的等量关系用分式方程表示。 难点 找实际问题中的等量关系。
教法及教具
教学过程 教 学 内 容 个案调整
教师主导活动 学生主体活动 教师板书出解分式方程的一般过程及完整的书写格式。
情境创设:1、甲、乙两人加工同一种服装,乙每天比甲多加工1件,已知乙加工24件服装所用时间与甲加工20件服装所用时间相同。甲每天加工多少件服装?2、一个两位数的各位数字是4,如果把各位数字与十位数字对调,那么所得的两位数与原两位数的比值是。原两位数的十位数字是几?3、某校学生到距离学校15km的山坡上植 ( http: / / www.21cnjy.com )树,一部分学生骑自行车出发40min后,另一部分学生乘汽车出发,结果全体学生同时到达。已知汽车的速度是自行车的速度的3倍,求自行车速度。二.新知探究:1、上面所得到的方程有什么共同特点?(学生可分组讨论交流)结论:分母中含有未知数的方程叫做分式方程。2、分式方程与整式方程有什么区别?3、探寻分式方程的解法:如何解分式方程=?指出:解分式方程的一般步骤是先去分母,把不熟悉的分式方程转化为熟悉的一元一次方程来解决。三.例题分析:例1 解方程:练一练:完成情境中的三个分式方程。 1.如果设甲每天加工件服装,那么乙每天加工______件服装,根据题意,可列出方程:___________________如果设原两位数的十位数字是,那么可以列出方程: 如果设自行车的速度是 km/h,那么可列出方程:
教学过程 教 学 内 容 个案调整
教师主导活动 学生主体活动
例2 从甲地到乙地有两条公路:一条是全长600 km的普通公路,另一条是全长480 km的高速公路。某客车在高速公路上行驶的平均速度比在普通公路上快45 km/h,由高速公路从甲地到乙地所需的时间是由普通公路从甲地到乙地所需时间的一半。求该客车由高速公路从甲地到乙地所需的时间。练习1、轮船在顺水中航行20千米与逆水航行10千米所用时间相同,水流速度为2.5千米/小时,求轮船的静水速度。若分式方程的一个解是,则 。3、解方程: 4.某农场开挖一条480米的渠道,开工后,每天比原计划多挖20米,结果提前4天完成任务,若设原计划每天挖米,那么求时所列方程正确的是( )A、 B、 C、 D、 五.小结
板书设计(用案人完成)
作业布置
教学札记
分式方程 第二课时
教学目标 1、经历探索分式方程解法的过程,会解可化为一元一次方程的分式方程。2、了解分式方程产生增根的原因,会检验根的合理性。
重点 分式方程的解法 难点 解分式方程要验根
教法及教具
教学过程 教 学 内 容 个案调整
教师主导活动 学生主体活动
情境创设:解方程:(1)(2)探索活动:1、方程(1)和方程(2)的求解步骤有差异吗?2、这两个方程有解吗?在这里,x=2是方程(2)的根吗?为什么?3、你认为在解分式方程的过程中,那一步变形可能引起增根? 产生增根的原因是:我们在方程的两边同乘了一个可能使分母为0的整式。因为解分式方程可能产生增根,所以解分式方程必须检验。你能用比较简洁的方法检验解分式方程产生的、想一想解分式方程一般需要经过哪几个步骤?二.例题分析:例1 解下列方程: (1) (2)总结:解分式方程的一般步骤:去分母(注意防止漏乘);去括号(注意先确定符号)有同类项及时的合并同类项;移项;未知数的系数化为1;验根(解分式方程必须要验根)。 2.说明:在这里,x=2不是原方程(2)的根,因为它使得原分式方程的分母为零,我们称它为原方程的增根。
教学过程 教 学 内 容 个案调整
教师主导活动 学生主体活动
课堂练习1、解方程: 2、填空(1)若关于x的方程的解是x=1,则m= ; (2)若方程有增根,则;3、选择(1)下列关于分式方程增根的说法正确的是 ( )A.使所有的分母的值都为零的解是增根 B.分式方程的解为零就是增根C.使分子的值为零的解就是增根 D.使最简公分母的值为零的解是增根(2)方程可能产生的增根是 ( ) A.1 B.2 C.-1或2 D.1或2 四.小结
板书设计(用案人完成)
作业布置
教学札记
分式方程 第三课时
教学目标 1、能将实际问题中的等量关系用分式方程表示,列出分式方程解决简单的实际问题,并能根据实际问题的意义检验所得的结果是否合理。2、发展学生分析问题、解决问题的能力,渗透数学的转化思想人体,培养学生的应用意识。
重点 如何结合实际分析问题,列出分式方程 难点 分析过程,得到等量关系
教法及教具
教学过程 教 学 内 容 个案调整
教师主导活动 学生主体活动
复习巩固:1、解分式方程的一般步骤有哪些?2、解方程:(1)= (2)+=2二.情境创设 甲、乙两地相距19千米,某人从甲地出发出乙地,先步行7千米,然后改骑自行车,共用2小时到达乙地。已知这个人骑自行车的速度是步行速度的4倍。若设这个人步行的速度为千米/小时, ⑴这个人步行时间为 小时,骑车时间为 小时。⑵求步行速度和骑自行车的速度。例题分析例1. 为迎接市中学生田径运动会,计划由某校八年级(1)班的3个小组制作240面彩旗,后因一个小组另有任务,改由另外两个小组完成制作彩旗的任务。这样,这两个小组的每个同学就要比原计划多做4面。如果这3个小组的人数相等,那么每个小组有多少名学生? 学生练习,板演,注意最后验根。先个人思考,再互相交流,尝试从不同角度寻求解决问题的方法,找出题中的等量关系,根据等量关系列出方程。
教学过程 教 学 内 容 个案调整
教师主导活动 学生主体活动
例2、甲、乙两公司各为“见义勇为基金会”捐 ( http: / / www.21cnjy.com )款30000元,已知乙公司比甲公司人均多捐款20元,且甲公司的人数比乙公司的人数多20%。问甲、乙两公司各有多少人?总结:用分式方程解实际问题的一般步骤:设未知数根据题意列方程解方程检验答课堂练习 1.为了帮助遭受自然灾害的地区重建家园,某学校号召同学们自愿捐款。已知第一次捐款总额为4800元,第二次捐款总额为5000元,第二次捐款人数比第一次多20人,而且两次人均捐款额恰好相等。如果设第一次捐款人数为人,那么满足怎样的方程? 2、为改善生态环境,防止水土流失,某村 ( http: / / www.21cnjy.com )拟在荒坡地上种植960棵树, 由于青年团员的支持,每日比原计划多种20棵,结果提前4天完成任务,原计划每天种植多少棵 五.小结
板书设计(用案人完成)
作业布置
教学札记
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
