6.2.2 余角和补角 课件(共20张PPT)2024—2025学年苏科版数学七年级上册
文档属性
| 名称 | 6.2.2 余角和补角 课件(共20张PPT)2024—2025学年苏科版数学七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-27 00:00:00 | ||
图片预览




文档简介
(共20张PPT)
6.2.2 余角和补角
第6章 基本的几何图形
1、了解补角、余角,知道同角(或等角)的补角相等, 同角(或等角)的余角相等;
2、能利用同角(或等角)的补角相等、同角(或等角)的余角相等的性质进行简单的计算和说理;
3、从数学的角度提出问题、理解问题,锻炼克服困难的意志.
学习目标
重点:理解互为补角、互为余角的定义,以及补角、余角的性质.
难点:运用互为补角和互为余角的定义以及补角、余角的性质,结合方程的思想解决相关问题.
如右图:坝底是由石块堆积而成,要测出∠1的度数,你有什么简单的方法吗
情景导入
活动探究
思考:
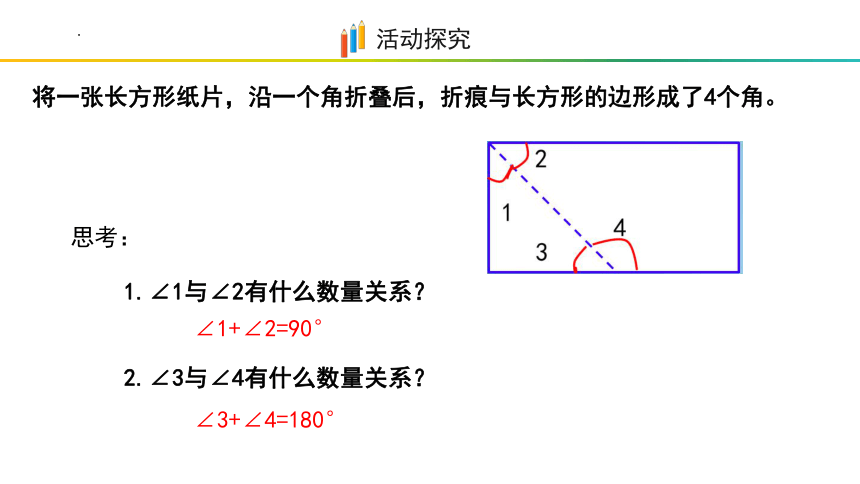
将一张长方形纸片,沿一个角折叠后,折痕与长方形的边形成了4个角。
1.∠1与∠2有什么数量关系?
2.∠3与∠4有什么数量关系?
∠1+∠2=90°
∠3+∠4=180°
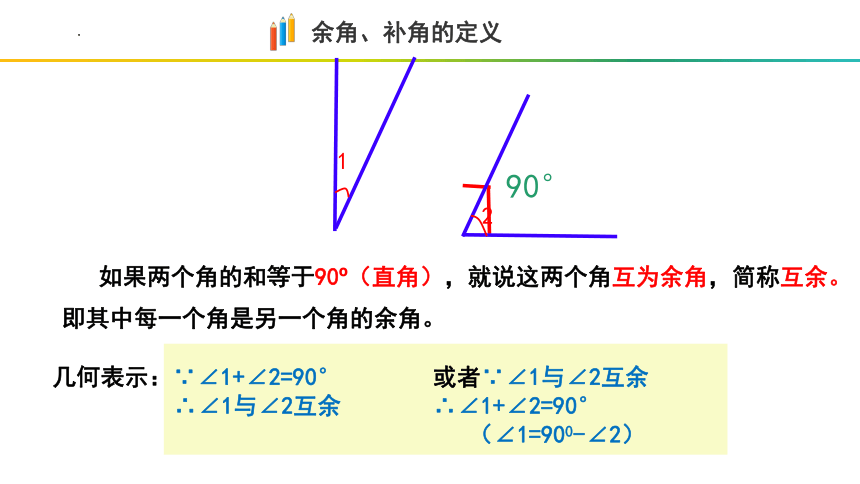
如果两个角的和等于90 (直角),就说这两个角互为余角,简称互余。
几何表示:∵∠1+∠2=90°
∴∠1与∠2互余
或者∵∠1与∠2互余 ∴∠1+∠2=90°
(∠1=900-∠2)
90°
1
2
余角、补角的定义
即其中每一个角是另一个角的余角。
探究新知
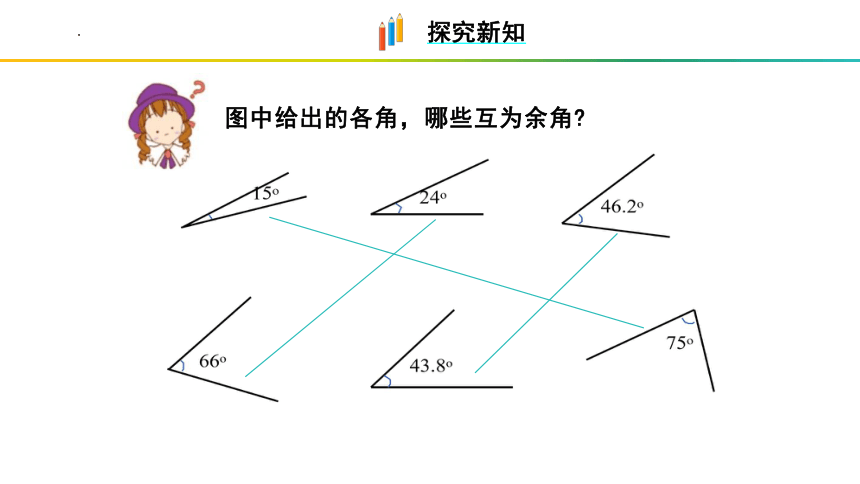
图中给出的各角,哪些互为余角
180°
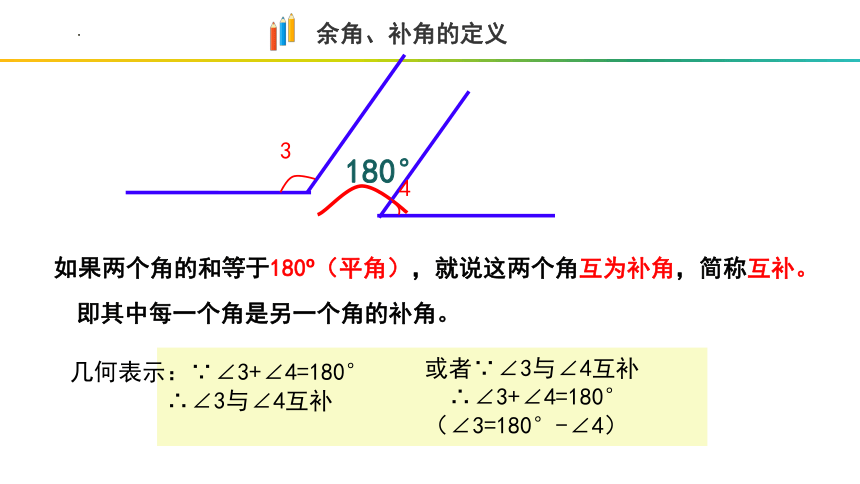
如果两个角的和等于180 (平角),就说这两个角互为补角,简称互补。
余角、补角的定义
几何表示:∵∠3+∠4=180°
∴∠3与∠4互补
或者∵∠3与∠4互补
∴∠3+∠4=180°
(∠3=180°-∠4)
3
4
即其中每一个角是另一个角的补角。
探究新知
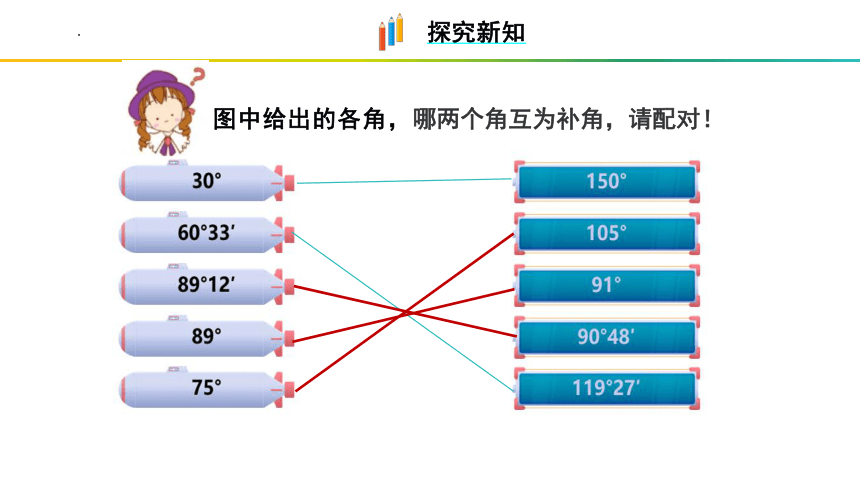
图中给出的各角,哪两个角互为补角,请配对!
例 1若一个角的补角等于它的余角的4倍,
求这个角的度数。
利用余角、补角的概念求角的度数
探究新知
例2 如图,已知0为AD上一点,∠AOC与∠AOB互补,OM,
ON分别为∠AOC,∠AOB 的平分线,若∠MON=40°,
试求:∠AOC与∠AOB的度数。
余角、补角、角平分线相结合的题目
探究新知
900
∠α ∠α的余角 ∠α的补角
80°
45°
70°39′
x(0°<x<90°)
探究新知
观察可得结论:锐角的补角比它的余角大
19°21′
10°
100°
45°
135°
109°21′
90°-x
180°-x
图1
如图1,打台球时,选择适当的方向用白球击打红球,反弹后的红球会直接入袋,此时∠1=∠2,将图1简化成图2,ON与DC交于点O,∠DON=∠CON=90°,∠1=∠2.
N
2
D
C
O
1
3
4
A
B
图2
活动探究
因为∠1= ∠2,
∠ 1+∠3=90°,
∠ 2+∠4=90°,
所以∠ 3=∠4.
解决下列问题:在图2中
∠3与∠4有什么关系?为什么?
解:∠ 3=∠4,
N
2
D
C
O
1
3
4
A
B
图2
同角(等角)的余角相等.
活动探究
因为∠1= ∠2,
∠1+∠AOC=180°,
∠ 2+∠BOD=180°,
所以∠AOC=∠BOD.
解:∠AOC=∠BOD,
N
2
D
C
O
1
3
4
A
B
图2
同角(等角)的补角相等.
解决下列问题:在图2中
(4)∠AOC与∠BOD有什么关系?为什么?
活动探究
1.如图,直线a、b相交,若∠1 = 40°,求 ∠2的度数.
解:由补角的定义, ∠1 = 40°可得
∠2 = 180°-∠1,
= 180°- 40°
= 140°.
1
2
3
4
b
a
当堂检测
2. 如图,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC=60°,
求∠BOC的度数.
O
D
C
B
A
E
解:因为OA平分∠EOC,∠EOC = 60°,
所以∠AOC = 30°,
由补角定义,得
∠BOC = 180°-∠AOC
= 180°- 30°
= 150°.
当堂检测
3.若一个角的补角等于它的余角的4 倍,求这个角的度数.
解:设这个角为x度.
则它的补角为(180-x)度,
它的余角为(90-x)度.
根据题意得:180-x=4(90-x),
解得: x =60,
即这个角为60度.
当堂检测
模型简介
观察并小组讨论:图中哪些角相等?为什么
补角
余角
如果两个角的和是90°,那么称这两个角互为余角.
同角或等角的余角相等.
如果两个角的和是180°,那么称这两个角互为补角.
同角或等角的补角相等.
课堂总结
互余与互补只与角的数值有关,与位置无关.
本课结束
6.2.2 余角和补角
第6章 基本的几何图形
1、了解补角、余角,知道同角(或等角)的补角相等, 同角(或等角)的余角相等;
2、能利用同角(或等角)的补角相等、同角(或等角)的余角相等的性质进行简单的计算和说理;
3、从数学的角度提出问题、理解问题,锻炼克服困难的意志.
学习目标
重点:理解互为补角、互为余角的定义,以及补角、余角的性质.
难点:运用互为补角和互为余角的定义以及补角、余角的性质,结合方程的思想解决相关问题.
如右图:坝底是由石块堆积而成,要测出∠1的度数,你有什么简单的方法吗
情景导入
活动探究
思考:
将一张长方形纸片,沿一个角折叠后,折痕与长方形的边形成了4个角。
1.∠1与∠2有什么数量关系?
2.∠3与∠4有什么数量关系?
∠1+∠2=90°
∠3+∠4=180°
如果两个角的和等于90 (直角),就说这两个角互为余角,简称互余。
几何表示:∵∠1+∠2=90°
∴∠1与∠2互余
或者∵∠1与∠2互余 ∴∠1+∠2=90°
(∠1=900-∠2)
90°
1
2
余角、补角的定义
即其中每一个角是另一个角的余角。
探究新知
图中给出的各角,哪些互为余角
180°
如果两个角的和等于180 (平角),就说这两个角互为补角,简称互补。
余角、补角的定义
几何表示:∵∠3+∠4=180°
∴∠3与∠4互补
或者∵∠3与∠4互补
∴∠3+∠4=180°
(∠3=180°-∠4)
3
4
即其中每一个角是另一个角的补角。
探究新知
图中给出的各角,哪两个角互为补角,请配对!
例 1若一个角的补角等于它的余角的4倍,
求这个角的度数。
利用余角、补角的概念求角的度数
探究新知
例2 如图,已知0为AD上一点,∠AOC与∠AOB互补,OM,
ON分别为∠AOC,∠AOB 的平分线,若∠MON=40°,
试求:∠AOC与∠AOB的度数。
余角、补角、角平分线相结合的题目
探究新知
900
∠α ∠α的余角 ∠α的补角
80°
45°
70°39′
x(0°<x<90°)
探究新知
观察可得结论:锐角的补角比它的余角大
19°21′
10°
100°
45°
135°
109°21′
90°-x
180°-x
图1
如图1,打台球时,选择适当的方向用白球击打红球,反弹后的红球会直接入袋,此时∠1=∠2,将图1简化成图2,ON与DC交于点O,∠DON=∠CON=90°,∠1=∠2.
N
2
D
C
O
1
3
4
A
B
图2
活动探究
因为∠1= ∠2,
∠ 1+∠3=90°,
∠ 2+∠4=90°,
所以∠ 3=∠4.
解决下列问题:在图2中
∠3与∠4有什么关系?为什么?
解:∠ 3=∠4,
N
2
D
C
O
1
3
4
A
B
图2
同角(等角)的余角相等.
活动探究
因为∠1= ∠2,
∠1+∠AOC=180°,
∠ 2+∠BOD=180°,
所以∠AOC=∠BOD.
解:∠AOC=∠BOD,
N
2
D
C
O
1
3
4
A
B
图2
同角(等角)的补角相等.
解决下列问题:在图2中
(4)∠AOC与∠BOD有什么关系?为什么?
活动探究
1.如图,直线a、b相交,若∠1 = 40°,求 ∠2的度数.
解:由补角的定义, ∠1 = 40°可得
∠2 = 180°-∠1,
= 180°- 40°
= 140°.
1
2
3
4
b
a
当堂检测
2. 如图,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC=60°,
求∠BOC的度数.
O
D
C
B
A
E
解:因为OA平分∠EOC,∠EOC = 60°,
所以∠AOC = 30°,
由补角定义,得
∠BOC = 180°-∠AOC
= 180°- 30°
= 150°.
当堂检测
3.若一个角的补角等于它的余角的4 倍,求这个角的度数.
解:设这个角为x度.
则它的补角为(180-x)度,
它的余角为(90-x)度.
根据题意得:180-x=4(90-x),
解得: x =60,
即这个角为60度.
当堂检测
模型简介
观察并小组讨论:图中哪些角相等?为什么
补角
余角
如果两个角的和是90°,那么称这两个角互为余角.
同角或等角的余角相等.
如果两个角的和是180°,那么称这两个角互为补角.
同角或等角的补角相等.
课堂总结
互余与互补只与角的数值有关,与位置无关.
本课结束
同课章节目录
