2.2.2 法拉第电磁感应定律的应用 导学案 -2024-2025学年高二上学期物理人教版(2019)选择性必修第二册
文档属性
| 名称 | 2.2.2 法拉第电磁感应定律的应用 导学案 -2024-2025学年高二上学期物理人教版(2019)选择性必修第二册 |
|
|
| 格式 | docx | ||
| 文件大小 | 567.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-11-27 00:00:00 | ||
图片预览


文档简介
第二章 电磁感应
2.2.2 法拉第电磁感应定律的应用
班级: 姓名:
1、进一步熟练掌握法拉第电磁感应定律、楞次定律。
2.掌握解决电磁感应现象中电路问题和电荷量问题的基本思路和方法。
3.综合应用楞次定律和法拉第电磁感应定律解决电磁感应中的图像问题。
4.进一步熟练掌握牛顿运动定律、动能定理、能量守恒定律等基本规律。
5.掌握电磁感应中动力学问题的分析方法,建立解决电磁感应中动力学问题的思维模型。
6.理解电磁感应过程中能量的转化情况,能用能量的观点分析和解决电磁感应问题。。
【学习任务一】电磁感应现象中的电路分析
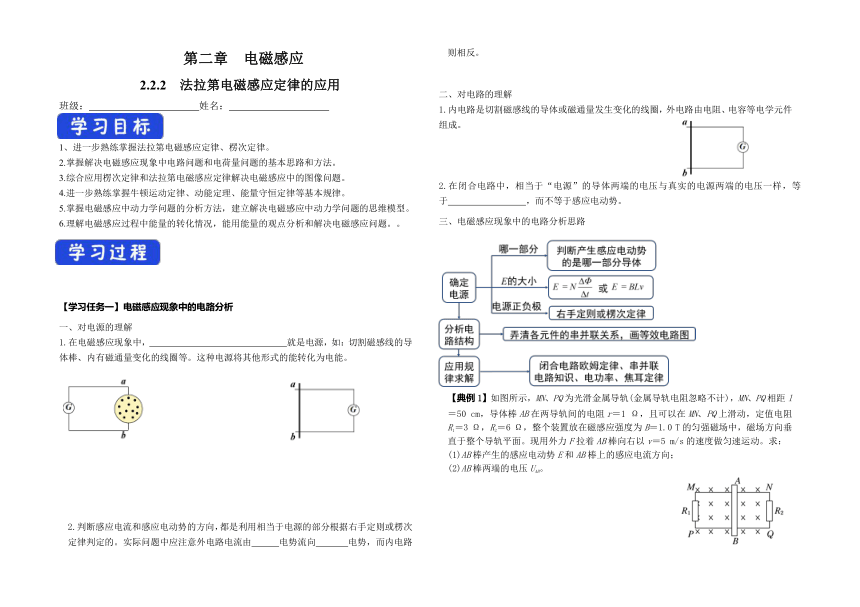
一、对电源的理解
1.在电磁感应现象中, 就是电源,如:切割磁感线的导体棒、内有磁通量变化的线圈等。这种电源将其他形式的能转化为电能。
2.判断感应电流和感应电动势的方向,都是利用相当于电源的部分根据右手定则或楞次定律判定的。实际问题中应注意外电路电流由 电势流向 电势,而内电路则相反。
二、对电路的理解
1.内电路是切割磁感线的导体或磁通量发生变化的线圈,外电路由电阻、电容等电学元件组成。
2.在闭合电路中,相当于“电源”的导体两端的电压与真实的电源两端的电压一样,等于 ,而不等于感应电动势。
三、电磁感应现象中的电路分析思路
【典例1】如图所示,MN、PQ为光滑金属导轨(金属导轨电阻忽略不计),MN、PQ相距l=50 cm,导体棒AB在两导轨间的电阻r=1 Ω,且可以在MN、PQ上滑动,定值电阻R1=3 Ω,R2=6 Ω,整个装置放在磁感应强度为B=1.0 T的匀强磁场中,磁场方向垂直于整个导轨平面。现用外力F拉着AB棒向右以v=5 m/s的速度做匀速运动。求:
(1)AB棒产生的感应电动势E和AB棒上的感应电流方向;
(2)AB棒两端的电压UAB。
【学习任务二】电磁感应中的电荷量问题
闭合回路中 发生变化时,电荷发生定向移动而形成感应电流,在Δt内通过某一截面的电荷量(感应电荷量)q=
推导过程:
(1)由上式可知,通过某一截面的感应电荷量q仅由 、回路电阻R和 决定,与时间长短无关。
(2)求解电路中通过的电荷量时,I、E 均为平均值.
【典例2】如图所示,通有恒定电流的长直导线MN与闭合金属线框abcd共面,电流方向为N→M。第一次将金属线框由位置Ⅰ平移到位置Ⅱ,第二次将金属线框由位置Ⅰ翻转到位置Ⅱ,设两次通过金属线框截面的电荷量分别为q1和q2,则( )
A.q1<q2
B.q1=q2
C.q1>q2
D.q1≠0,q2=0
【学习任务三】电磁感应中的图像问题
1.图像类型
(1)各物理量随时间t变化的图像,即B-t图像、Φ-t图像、E-t图像和I-t图像.
(2)导体做切割磁感线运动时,还涉及感应电动势E和感应电流I随导体位移变化的图像,即E-x图像和I-x图像.
2.解决此类问题需要熟练掌握的规律
安培定则、左手定则、楞次定律、右手定则、法拉第电磁感应定律、欧姆定律等.判断物理量增大、减小、正负等,必要时写出函数关系式,进行分析.
3.解决此类问题的一般步骤
【典例3】如图甲,MN、PQ两条平行的光滑金属轨道与水平面成θ=37°固定,M、P之间接电阻箱R,导轨所在空间存在匀强磁场,磁场方向垂直于轨道平面向上,磁感应强度为B=0.5T。质量为m的金属杆ab水平放置在轨道上,其接入电路的阻值为r。现从静止释放杆ab,测得其最大速度为vm。改变电阻箱的阻值R,得到vm与R的关系如图乙所示。已知两条轨道间的距离为L=2m,重力加速度g取10m/s2,轨道足够长且电阻不计,sin37°=0.6,cos37°=0.8,求:(1)杆ab下滑过程中感应电流的方向及R=0时最大感应电动势的大小;
(2)金属杆的质量m和阻值r;
(3)当R=4 时,求回路瞬时电功率每增加1W的过程中合外力对杆做的功W。
【学习任务四】电磁感应现象中的综合问题分析
1.导体的两种运动状态
(1)导体的平衡状态——静止状态或匀速直线运动状态。处理方法:根据平衡条件(合外力等于0)列式分析。
(2)导体的非平衡状态——加速度不为0。处理方法:根据牛顿第二定律进行动态分析或结合功能关系分析。
2.制约关系
【典例4】如图甲所示,两根足够长的直金属导轨MN、PQ平行放置在倾角为θ的绝缘斜面上,两导轨间距为l,M、P两点间接有阻值为R的电阻。一根质量为m的均匀直金属杆ab放在两导轨上,并与导轨垂直。整套装置处于磁感应强度为B的匀强磁场中,磁场方向垂直斜面向下。导轨和金属杆的电阻可忽略。让ab杆沿导轨由静止开始下滑,导轨和金属杆接触良好,不计它们之间的摩擦。
(1) 在加速下滑过程中,当ab杆的速度大小为v时,求此时ab杆中的电流及其加速度的大小。
(2)求在下滑过程中,ab杆可以达到的速度最大值。
1.能量转化的过程分析
电磁感应的实质是不同形式的能量转化的过程,而能量的转化是通过安培力做功实现的。安培力做功使得电能转化为其他形式的能(通常为内能),克服安培力做功,则是其他形式的能(通常为机械能)转化为电能的过程。
2.电磁感应中焦耳热的计算思路
(1)电流恒定时,根据焦耳定律 求解。
(2)电流变化时,用以下方法分析
①利用动能定理,求出安培力做的功W安,
产生的焦耳热等于克服安培力所做的功,即Q=-W安
②利用能量守恒,焦耳热与其他形式能量的总和保持不变。
【典例5】如图所示,一对光滑的平行金属导轨固定在同一水平面内,导轨间距l=0.5 m,左端接有阻值R=0.3 Ω的电阻。一质量m=0.1 kg、电阻r=0.1 Ω的金属棒MN放置在导轨上,整个装置置于竖直向上的匀强磁场中,磁场的磁感应强度B=0.4 T。棒在水平向右的外力作用下,由静止开始以a=2 m/s2的加速度做匀加速运动,当棒的位移x=9 m时撤去外力,棒继续运动一段距离后停下来,已知撤去外力前后回路中产生的焦耳热之比Q1∶Q2=2∶1。导轨足够长且电阻不计,棒在运动过程中始终与导轨垂直且两端与导轨保持良好接触。求:
(1)棒在匀加速运动过程中,通过电阻R的电荷量q;
(2)撤去外力后回路中产生的焦耳热Q2;
(3)外力所做的功WF。
.
2.2.2 法拉第电磁感应定律的应用
班级: 姓名:
1、进一步熟练掌握法拉第电磁感应定律、楞次定律。
2.掌握解决电磁感应现象中电路问题和电荷量问题的基本思路和方法。
3.综合应用楞次定律和法拉第电磁感应定律解决电磁感应中的图像问题。
4.进一步熟练掌握牛顿运动定律、动能定理、能量守恒定律等基本规律。
5.掌握电磁感应中动力学问题的分析方法,建立解决电磁感应中动力学问题的思维模型。
6.理解电磁感应过程中能量的转化情况,能用能量的观点分析和解决电磁感应问题。。
【学习任务一】电磁感应现象中的电路分析
一、对电源的理解
1.在电磁感应现象中, 就是电源,如:切割磁感线的导体棒、内有磁通量变化的线圈等。这种电源将其他形式的能转化为电能。
2.判断感应电流和感应电动势的方向,都是利用相当于电源的部分根据右手定则或楞次定律判定的。实际问题中应注意外电路电流由 电势流向 电势,而内电路则相反。
二、对电路的理解
1.内电路是切割磁感线的导体或磁通量发生变化的线圈,外电路由电阻、电容等电学元件组成。
2.在闭合电路中,相当于“电源”的导体两端的电压与真实的电源两端的电压一样,等于 ,而不等于感应电动势。
三、电磁感应现象中的电路分析思路
【典例1】如图所示,MN、PQ为光滑金属导轨(金属导轨电阻忽略不计),MN、PQ相距l=50 cm,导体棒AB在两导轨间的电阻r=1 Ω,且可以在MN、PQ上滑动,定值电阻R1=3 Ω,R2=6 Ω,整个装置放在磁感应强度为B=1.0 T的匀强磁场中,磁场方向垂直于整个导轨平面。现用外力F拉着AB棒向右以v=5 m/s的速度做匀速运动。求:
(1)AB棒产生的感应电动势E和AB棒上的感应电流方向;
(2)AB棒两端的电压UAB。
【学习任务二】电磁感应中的电荷量问题
闭合回路中 发生变化时,电荷发生定向移动而形成感应电流,在Δt内通过某一截面的电荷量(感应电荷量)q=
推导过程:
(1)由上式可知,通过某一截面的感应电荷量q仅由 、回路电阻R和 决定,与时间长短无关。
(2)求解电路中通过的电荷量时,I、E 均为平均值.
【典例2】如图所示,通有恒定电流的长直导线MN与闭合金属线框abcd共面,电流方向为N→M。第一次将金属线框由位置Ⅰ平移到位置Ⅱ,第二次将金属线框由位置Ⅰ翻转到位置Ⅱ,设两次通过金属线框截面的电荷量分别为q1和q2,则( )
A.q1<q2
B.q1=q2
C.q1>q2
D.q1≠0,q2=0
【学习任务三】电磁感应中的图像问题
1.图像类型
(1)各物理量随时间t变化的图像,即B-t图像、Φ-t图像、E-t图像和I-t图像.
(2)导体做切割磁感线运动时,还涉及感应电动势E和感应电流I随导体位移变化的图像,即E-x图像和I-x图像.
2.解决此类问题需要熟练掌握的规律
安培定则、左手定则、楞次定律、右手定则、法拉第电磁感应定律、欧姆定律等.判断物理量增大、减小、正负等,必要时写出函数关系式,进行分析.
3.解决此类问题的一般步骤
【典例3】如图甲,MN、PQ两条平行的光滑金属轨道与水平面成θ=37°固定,M、P之间接电阻箱R,导轨所在空间存在匀强磁场,磁场方向垂直于轨道平面向上,磁感应强度为B=0.5T。质量为m的金属杆ab水平放置在轨道上,其接入电路的阻值为r。现从静止释放杆ab,测得其最大速度为vm。改变电阻箱的阻值R,得到vm与R的关系如图乙所示。已知两条轨道间的距离为L=2m,重力加速度g取10m/s2,轨道足够长且电阻不计,sin37°=0.6,cos37°=0.8,求:(1)杆ab下滑过程中感应电流的方向及R=0时最大感应电动势的大小;
(2)金属杆的质量m和阻值r;
(3)当R=4 时,求回路瞬时电功率每增加1W的过程中合外力对杆做的功W。
【学习任务四】电磁感应现象中的综合问题分析
1.导体的两种运动状态
(1)导体的平衡状态——静止状态或匀速直线运动状态。处理方法:根据平衡条件(合外力等于0)列式分析。
(2)导体的非平衡状态——加速度不为0。处理方法:根据牛顿第二定律进行动态分析或结合功能关系分析。
2.制约关系
【典例4】如图甲所示,两根足够长的直金属导轨MN、PQ平行放置在倾角为θ的绝缘斜面上,两导轨间距为l,M、P两点间接有阻值为R的电阻。一根质量为m的均匀直金属杆ab放在两导轨上,并与导轨垂直。整套装置处于磁感应强度为B的匀强磁场中,磁场方向垂直斜面向下。导轨和金属杆的电阻可忽略。让ab杆沿导轨由静止开始下滑,导轨和金属杆接触良好,不计它们之间的摩擦。
(1) 在加速下滑过程中,当ab杆的速度大小为v时,求此时ab杆中的电流及其加速度的大小。
(2)求在下滑过程中,ab杆可以达到的速度最大值。
1.能量转化的过程分析
电磁感应的实质是不同形式的能量转化的过程,而能量的转化是通过安培力做功实现的。安培力做功使得电能转化为其他形式的能(通常为内能),克服安培力做功,则是其他形式的能(通常为机械能)转化为电能的过程。
2.电磁感应中焦耳热的计算思路
(1)电流恒定时,根据焦耳定律 求解。
(2)电流变化时,用以下方法分析
①利用动能定理,求出安培力做的功W安,
产生的焦耳热等于克服安培力所做的功,即Q=-W安
②利用能量守恒,焦耳热与其他形式能量的总和保持不变。
【典例5】如图所示,一对光滑的平行金属导轨固定在同一水平面内,导轨间距l=0.5 m,左端接有阻值R=0.3 Ω的电阻。一质量m=0.1 kg、电阻r=0.1 Ω的金属棒MN放置在导轨上,整个装置置于竖直向上的匀强磁场中,磁场的磁感应强度B=0.4 T。棒在水平向右的外力作用下,由静止开始以a=2 m/s2的加速度做匀加速运动,当棒的位移x=9 m时撤去外力,棒继续运动一段距离后停下来,已知撤去外力前后回路中产生的焦耳热之比Q1∶Q2=2∶1。导轨足够长且电阻不计,棒在运动过程中始终与导轨垂直且两端与导轨保持良好接触。求:
(1)棒在匀加速运动过程中,通过电阻R的电荷量q;
(2)撤去外力后回路中产生的焦耳热Q2;
(3)外力所做的功WF。
.
