3.6 角(第3课时 余角和补角) 课件(共40张PPT) -七年级数学上册考试满分全攻略同步备课备考系列(华师大版2024)
文档属性
| 名称 | 3.6 角(第3课时 余角和补角) 课件(共40张PPT) -七年级数学上册考试满分全攻略同步备课备考系列(华师大版2024) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-27 18:05:43 | ||
图片预览






文档简介
(共40张PPT)
华师大版(2024)七年级数学上册 第三章 图形的初步认识
3.6 角
第三课时 余角和补角
目录/CONTENTS
新知探究
情景导入
学习目标
课堂反馈
分层练习
课堂小结
学习目标
1. 知道两角互余、两角互补的意义,能熟练地求出一个角的余角或补角.
2. 通过探究,知道“同角(或等角)的余角相等”,“同角(或等角)的补角相等”,并会应用.
重点:余角、补角的概念及性质.
难点:余角、补角的性质.
情景导入
在我们所用的一副三角尺中,每块都有一个角是 90°,而其他两个角,一块 是 30°与 60°,另一块都是 45°,它们的和都是 90°.
新知探究
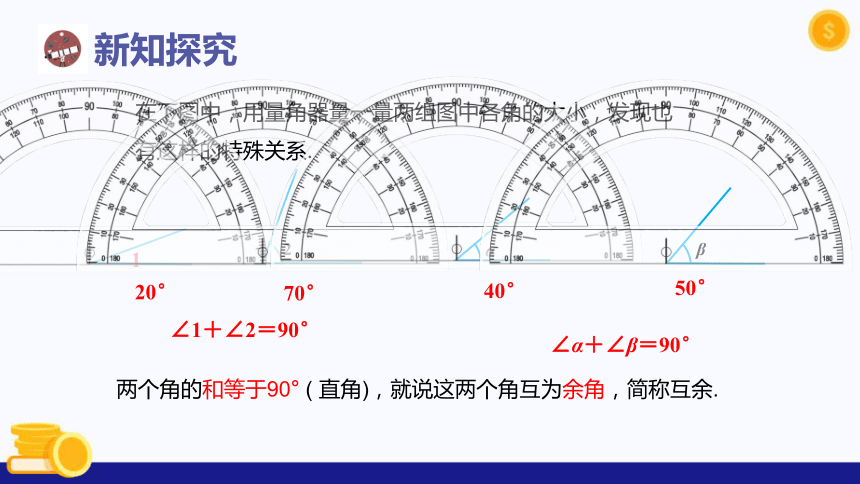
在下图中,用量角器量一量两组图中各角的大小,发现也有这样的特殊关系.
1
2
α
β
20°
70°
40°
50°
∠1+∠2=90°
∠α+∠β=90°
两个角的和等于90° ( 直角),就说这两个角互为余角,简称互余.
新知探究
两个角的和等于90° ( 直角),就说这两个角互为余角,简称互余.
例如,如果∠1+∠2=90°,那么∠1是∠2的余角,∠2也是∠1的余角.
反过来, 如果两个角互余,那么把这两个角如下图那样拼在一起的话,就构成一个直角.
新知探究
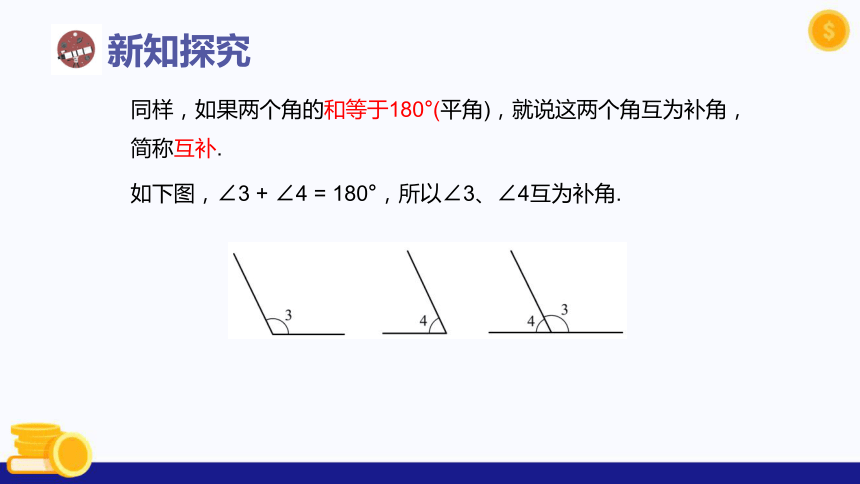
同样,如果两个角的和等于180°(平角),就说这两个角互为补角,简称互补.
如下图,∠3 + ∠4 = 180°,所以∠3、∠4互为补角.
新知探究
1
2
3
4
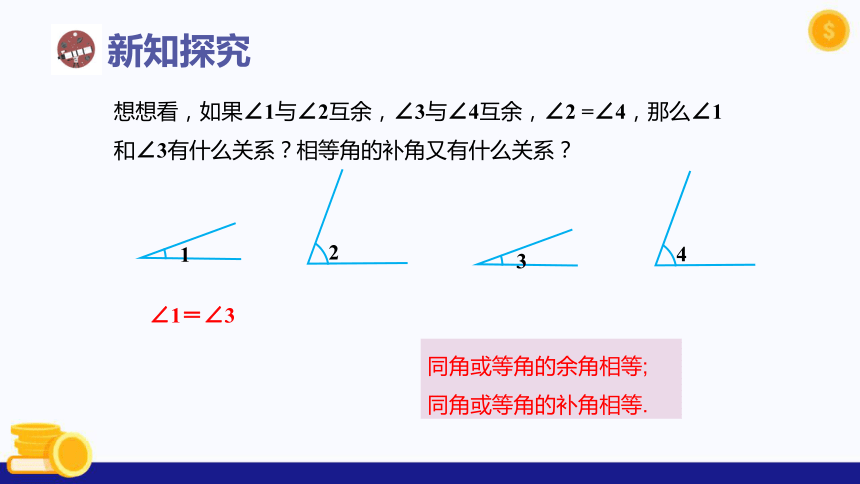
想想看,如果∠1与∠2互余,∠3与∠4互余,∠2 =∠4,那么∠1和∠3有什么关系?相等角的补角又有什么关系?
∠1=∠3
同角或等角的余角相等; 同角或等角的补角相等.
课本例题
例3 已知∠α=50°17′,求∠α的余角和补角.
解:∠α的余角=90°-50°17′=39°43′
∠α的补角=180°-50°17′=129°43′
课堂练习
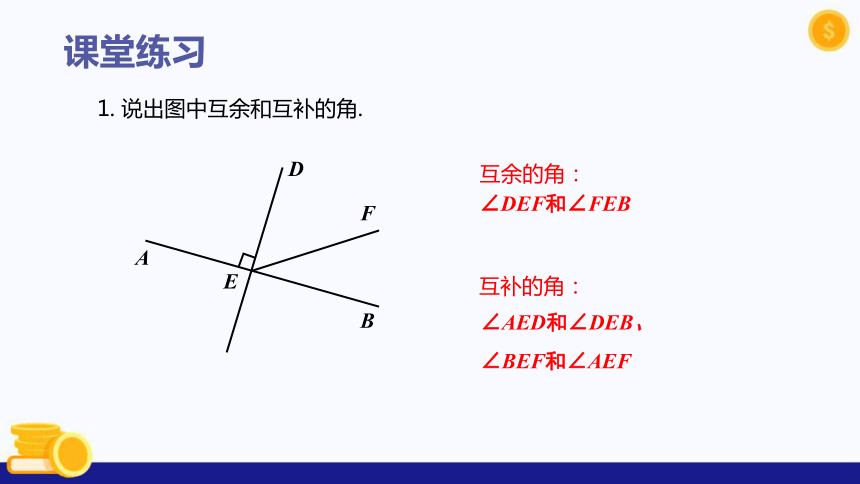
1. 说出图中互余和互补的角.
E
A
B
F
D
∠AED和∠DEB、
∠BEF和∠AEF
互补的角:
∠DEF和∠FEB
互余的角:
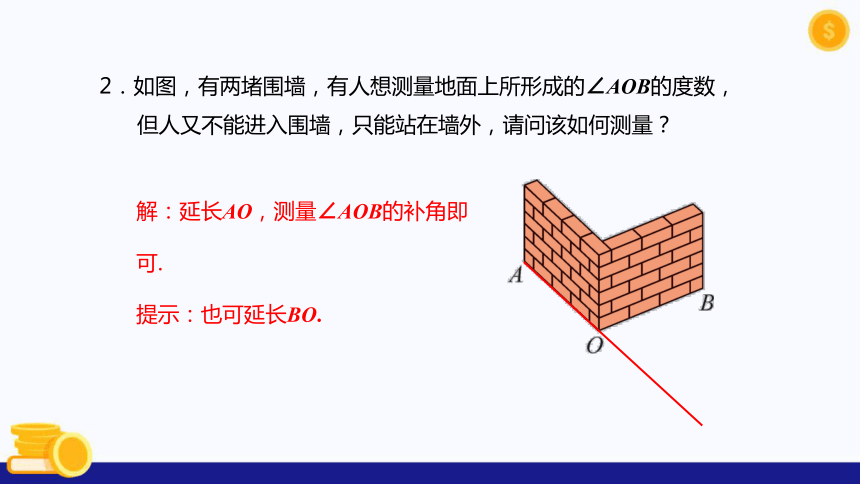
2.如图,有两堵围墙,有人想测量地面上所形成的∠AOB的度数,但人又不能进入围墙,只能站在墙外,请问该如何测量?
解:延长AO,测量∠AOB的补角即可.
提示:也可延长BO.
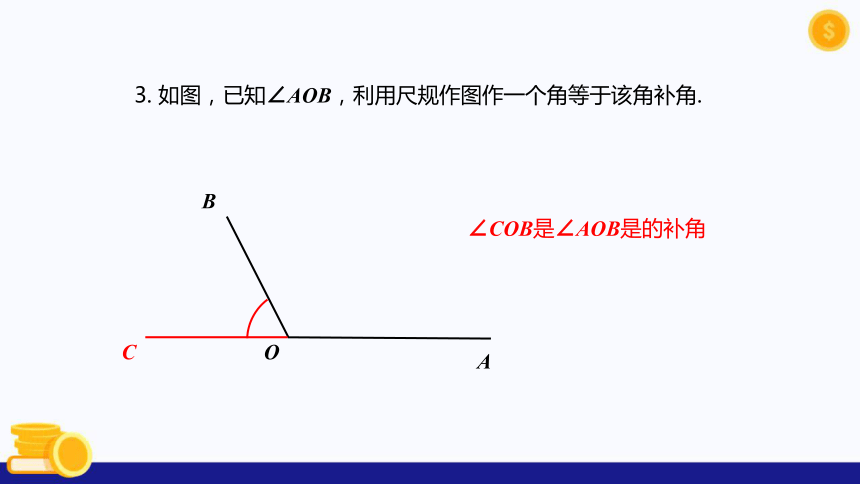
3. 如图,已知∠AOB,利用尺规作图作一个角等于该角补角.
B
O
A
C
∠COB是∠AOB是的补角
习题 3.6
1. 填空:
(1)77°42′+34°45′= ;
(2)108°18′-56°23′= ;
(3)180°- (34°54′+ 21°33′) = .
112°27′
51°55′
123°33′
2. 时钟的分针,1小时转了 度的角,
1 分钟转了 度的角.
6
360
3. 如图,如果∠1=65°15′,∠2=78°30′,则∠3是多少度
解:因为∠1=65°15′,∠2= 78°30′,
所以∠3=180°-∠1-∠2=36°15′.
4. 任意画一个∠AOB,在∠AOB的内部引射线OC、OD,这时图中共有几个角 分别把它们表示出来.
解:如图,这时图中共有6个角.
分别为∠AOC,∠AOD,∠AOB,
∠COD,∠COB,∠DOB.
5. 两个相等的钝角有同一个顶点和一条公共边,并且两个角的另一条边所成的角为90°,画出图形,并求出该钝角的大小.
B
A
C
O
解:如图,∠AOC和∠BOC即为所求.
因为∠AOB=90°,
所以∠AOC=∠BOC= ×(360°-90°)=135°.
6. 如图,OA是表示什么方向的一条射线?仿照这条射线画出表示下列方向的射线:
(1)南偏东60°;
(2)北偏西70°;
(3)西南方向(即南偏西45°).
解:OA表示北偏东40°方向的一条射线.
如图,射线OB、OC、OD即为所求.
东
西
南
北
O
A
40°
C
70°
B
60°
45°
D
7. 72°20′的角的余角等于 ;
25°31′的角的补角等于 .
17°40′
154°29′
8. 在图中,EF、EG分别是∠AEB和∠BEC的平分线,求∠GEF的度数,并写出∠BEF的余角.
解:因为EF、EG分别平分∠AEB和∠BEC,
所以∠BEF= ∠AEB,∠BEG= ∠BEC,
所以∠GEF=∠BEF+∠BEG
= (∠AEB+∠BEC)=90°.
∠BEF的余角是∠BEG,∠CEG.
9. 如图,已知∠A和∠ B,利用尺规作图作∠ C,使∠ C= ∠ A+ ∠ B.
A
B
C
分层练习-基础
知识点1 余角和补角的定义
1. [新趋势·跨学科 2024 扬州期末]冬至是地球赤道以北地区
白昼最短、黑夜最长的一天,在民间有“冬至大如年”的
说法.某地冬至日正午太阳高度角是32°24',则32°24'的
余角为 .
57°36'
2. 如果一个角的度数比它补角的2倍多30°,那么这个角的
度数是( C )
A. 50° B. 70°
C. 130° D. 160°
【点拨】
设这个角的度数是 x °.
根据题意,得 x =2(180- x )+30,
解得 x =130,即这个角的度数是130°.
C
3. [2024·广州越秀区月考]将一副三角尺按下列位置摆放,使∠α和∠β互余的摆放方式是( A )
对于A. ∠α+∠β=180°-90°=90°,∠α与∠β互余;对于B. 同角的余角相等,则∠α=∠β,但∠α与∠β不一定互余;对于C. ∠α=∠β=180°-45°=135°,∠α与∠β不互余;对于D. ∠α+∠β=180°,∠α与∠β不互余,故选A.
【点拨】
【答案】A
知识点2 余角和补角的性质
4. 如图,直线 AB , CD 交于点 O ,因为∠1+∠3=180°,
∠2+∠3=180°,所以∠1=∠2.此判断的依据是
( C )
A. 同角的余角相等 B. 等角的余角相等
C. 同角的补角相等 D. 等角的补角相等
(第4题)
C
5. 如图,点 C , O , B 在同一条直线上,∠ AOB =90°,
∠1=∠2,则下列结论:①∠ EOD =90°;②∠3=∠4;③∠2=∠3;④∠2+∠3=90°.其中正确的有
( C )
A. 1个 B. 2个
C. 3个 D. 4个
(第5题)
【点拨】
因为∠ AOB =90°,所以∠2+∠4=90°,
又因为∠1=∠2,所以∠1+∠4=∠ EOD =90°,
故①正确;
因为∠ AOC =180°-∠ AOB =90°,
所以∠1+∠3=90°.
所以∠3=∠4,故②正确;
因为∠ EOD =90°,
所以∠2+∠3=180°-90°=90°,∠2与∠3不一不相等,
故③错误,④正确.综上,正确的有3个,故选C.
【答案】C
6. [2023·衢州]如图是脊柱侧弯的检测示意图,在体检时为方
便测出 Cobb 角∠ O 的大小,需将∠ O 转化为与它相等的
角,则图中与∠ O 相等的角是( B )
A. ∠ BEA B. ∠ DEB
C. ∠ ECA D. ∠ ADO
B
7. 如图,∠ AOB =120°, OF 平分∠ AOB ,2∠1=∠2.
(1)∠1与∠2互余吗?试说明理由.
【解】∠1与∠2互余.理由如下:
因为∠ AOB =120°, OF 平分∠ AOB ,
所以∠2= ∠ AOB =60°.
因为2∠1=∠2,所以∠1=30°.
所以∠1+∠2=90°,即∠1与∠2互余.
(2)∠2与∠ AOB 互补吗?试说明理由.
【解】∠2与∠ AOB 互补.理由如下:
因为∠2+∠ AOB =60°+120°=180°,
所以∠2与∠ AOB 互补.
易错点 对余角和补角的定义理解不透彻而致错
8. 下列说法中,正确的有 .(填序号)
①钝角与锐角互补;
②∠α的余角是90°-∠α;
③∠β的补角是180°-∠β;
④若∠1+∠2+∠3=90°,则∠1,∠2,∠3互余.
②③
分层练习-巩固
利用余角、补角的定义找图中互为余角、补角的角
9. 如图,点 A , O , B 在同一条直线上,∠ AOD =∠ BOD
=∠ EOC =90°,∠ BOC ∶∠ AOE =3∶1.
(1)求∠ COD 的度数.
【解】由点 A , O , B 在同一条直线
上得∠ AOB =180°.
因为∠ EOC =90°,
所以∠ AOE +∠ BOC =180°-90°=90°.
又因为∠ BOC ∶∠ AOE =3∶1,
所以∠ BOC =90°× =67.5°.
所以∠ COD =∠ BOD -∠ BOC
=90°-67.5°=22.5°.
(2)图中有哪几对角互为余角?
【解】∠ AOE 与∠ DOE ,
∠ AOE 与∠ BOC ,
∠ DOE 与∠ DOC ,
∠ DOC 与∠ BOC ,这4对角互为余角.
(3)图中有哪几对角互为补角?
【解】∠ AOE 与∠ EOB ,
∠ AOD 与∠ DOB ,∠ AOC 与∠ BOC ,
∠ EOD 与∠ AOC ,∠ DOC 与∠ EOB ,
∠ AOD 与∠ EOC ,∠ BOD 与∠ EOC ,
这7对角互为补角.
分层练习-拓展
利用角的运算探求折叠中角的关系
10. [新考法 折叠法]如图,把一张长方形纸片的一角任意折
向长方形内,使点 B 落在点B'的位置,折痕为 EF ;再沿
GF 折叠,使点 C 落在点C'的位置,点 D 落在D'的位置,
如果C'F与FB'在同一条直线上.
(1)分别写出∠1与∠ CFE 、∠2与∠ BFG 之间所满足的
数量关系.
【解】∠1+∠ CFE =180°,∠2+∠ BFG =180°.
(2)写出∠1与∠2之间的数量关系.
【解】∠1=90°-∠2.(或∠1+∠2
=90°或∠2=90°-∠1)
(3)∠ EFG 是什么角?
【解】∠ EFG 是直角.
利用角互余、互补关系探究角的关系
11. [新考法 探究比较法]如图①,∠ AOB =∠ COD =90°.
(1)若∠ BOC =2∠ AOC ,求∠ BOC 的大小.
【解】因为∠ AOB =90°,
所以∠ BOC +∠ AOC =90°.
因为∠ BOC =2∠ AOC ,所以∠ BOC =60°.
(2)试探究∠ BOC 与∠ AOD 之间的数量关系.
【解】因为∠ COD =90°,
所以∠ AOD =∠ COD +∠ AOC =90°+∠ AOC .
因为∠ AOB =90°,
所以∠ BOC +∠ AOC =90°.
所以∠ BOC +∠ AOD =∠ BOC +90°+∠ AOC =
90°+90°=180°,
即∠ BOC +∠ AOD =180°.
(3)若把图①中∠ AOB 绕点 O 旋转到图②的位置,(2)中∠ BOC 与∠ AOD 之间的数量关系还成立吗?试说明理由.
【解】成立.理由:因为∠ AOB =∠ COD =90°,
所以∠ AOB +∠ COD =180°.
因为∠ BOC +∠ AOD +∠ AOB +∠ COD =360°,
所以∠ BOC +∠ AOD =180°.
课堂小结
互 余 互 补
数量 关系
对 应 图 形
性 质
∠1+∠2=90°
∠3+∠4=180°
同角或等角的余角相等
同角或等角的补角相等
华师大版(2024)七年级数学上册 第三章 图形的初步认识
3.6 角
第三课时 余角和补角
目录/CONTENTS
新知探究
情景导入
学习目标
课堂反馈
分层练习
课堂小结
学习目标
1. 知道两角互余、两角互补的意义,能熟练地求出一个角的余角或补角.
2. 通过探究,知道“同角(或等角)的余角相等”,“同角(或等角)的补角相等”,并会应用.
重点:余角、补角的概念及性质.
难点:余角、补角的性质.
情景导入
在我们所用的一副三角尺中,每块都有一个角是 90°,而其他两个角,一块 是 30°与 60°,另一块都是 45°,它们的和都是 90°.
新知探究
在下图中,用量角器量一量两组图中各角的大小,发现也有这样的特殊关系.
1
2
α
β
20°
70°
40°
50°
∠1+∠2=90°
∠α+∠β=90°
两个角的和等于90° ( 直角),就说这两个角互为余角,简称互余.
新知探究
两个角的和等于90° ( 直角),就说这两个角互为余角,简称互余.
例如,如果∠1+∠2=90°,那么∠1是∠2的余角,∠2也是∠1的余角.
反过来, 如果两个角互余,那么把这两个角如下图那样拼在一起的话,就构成一个直角.
新知探究
同样,如果两个角的和等于180°(平角),就说这两个角互为补角,简称互补.
如下图,∠3 + ∠4 = 180°,所以∠3、∠4互为补角.
新知探究
1
2
3
4
想想看,如果∠1与∠2互余,∠3与∠4互余,∠2 =∠4,那么∠1和∠3有什么关系?相等角的补角又有什么关系?
∠1=∠3
同角或等角的余角相等; 同角或等角的补角相等.
课本例题
例3 已知∠α=50°17′,求∠α的余角和补角.
解:∠α的余角=90°-50°17′=39°43′
∠α的补角=180°-50°17′=129°43′
课堂练习
1. 说出图中互余和互补的角.
E
A
B
F
D
∠AED和∠DEB、
∠BEF和∠AEF
互补的角:
∠DEF和∠FEB
互余的角:
2.如图,有两堵围墙,有人想测量地面上所形成的∠AOB的度数,但人又不能进入围墙,只能站在墙外,请问该如何测量?
解:延长AO,测量∠AOB的补角即可.
提示:也可延长BO.
3. 如图,已知∠AOB,利用尺规作图作一个角等于该角补角.
B
O
A
C
∠COB是∠AOB是的补角
习题 3.6
1. 填空:
(1)77°42′+34°45′= ;
(2)108°18′-56°23′= ;
(3)180°- (34°54′+ 21°33′) = .
112°27′
51°55′
123°33′
2. 时钟的分针,1小时转了 度的角,
1 分钟转了 度的角.
6
360
3. 如图,如果∠1=65°15′,∠2=78°30′,则∠3是多少度
解:因为∠1=65°15′,∠2= 78°30′,
所以∠3=180°-∠1-∠2=36°15′.
4. 任意画一个∠AOB,在∠AOB的内部引射线OC、OD,这时图中共有几个角 分别把它们表示出来.
解:如图,这时图中共有6个角.
分别为∠AOC,∠AOD,∠AOB,
∠COD,∠COB,∠DOB.
5. 两个相等的钝角有同一个顶点和一条公共边,并且两个角的另一条边所成的角为90°,画出图形,并求出该钝角的大小.
B
A
C
O
解:如图,∠AOC和∠BOC即为所求.
因为∠AOB=90°,
所以∠AOC=∠BOC= ×(360°-90°)=135°.
6. 如图,OA是表示什么方向的一条射线?仿照这条射线画出表示下列方向的射线:
(1)南偏东60°;
(2)北偏西70°;
(3)西南方向(即南偏西45°).
解:OA表示北偏东40°方向的一条射线.
如图,射线OB、OC、OD即为所求.
东
西
南
北
O
A
40°
C
70°
B
60°
45°
D
7. 72°20′的角的余角等于 ;
25°31′的角的补角等于 .
17°40′
154°29′
8. 在图中,EF、EG分别是∠AEB和∠BEC的平分线,求∠GEF的度数,并写出∠BEF的余角.
解:因为EF、EG分别平分∠AEB和∠BEC,
所以∠BEF= ∠AEB,∠BEG= ∠BEC,
所以∠GEF=∠BEF+∠BEG
= (∠AEB+∠BEC)=90°.
∠BEF的余角是∠BEG,∠CEG.
9. 如图,已知∠A和∠ B,利用尺规作图作∠ C,使∠ C= ∠ A+ ∠ B.
A
B
C
分层练习-基础
知识点1 余角和补角的定义
1. [新趋势·跨学科 2024 扬州期末]冬至是地球赤道以北地区
白昼最短、黑夜最长的一天,在民间有“冬至大如年”的
说法.某地冬至日正午太阳高度角是32°24',则32°24'的
余角为 .
57°36'
2. 如果一个角的度数比它补角的2倍多30°,那么这个角的
度数是( C )
A. 50° B. 70°
C. 130° D. 160°
【点拨】
设这个角的度数是 x °.
根据题意,得 x =2(180- x )+30,
解得 x =130,即这个角的度数是130°.
C
3. [2024·广州越秀区月考]将一副三角尺按下列位置摆放,使∠α和∠β互余的摆放方式是( A )
对于A. ∠α+∠β=180°-90°=90°,∠α与∠β互余;对于B. 同角的余角相等,则∠α=∠β,但∠α与∠β不一定互余;对于C. ∠α=∠β=180°-45°=135°,∠α与∠β不互余;对于D. ∠α+∠β=180°,∠α与∠β不互余,故选A.
【点拨】
【答案】A
知识点2 余角和补角的性质
4. 如图,直线 AB , CD 交于点 O ,因为∠1+∠3=180°,
∠2+∠3=180°,所以∠1=∠2.此判断的依据是
( C )
A. 同角的余角相等 B. 等角的余角相等
C. 同角的补角相等 D. 等角的补角相等
(第4题)
C
5. 如图,点 C , O , B 在同一条直线上,∠ AOB =90°,
∠1=∠2,则下列结论:①∠ EOD =90°;②∠3=∠4;③∠2=∠3;④∠2+∠3=90°.其中正确的有
( C )
A. 1个 B. 2个
C. 3个 D. 4个
(第5题)
【点拨】
因为∠ AOB =90°,所以∠2+∠4=90°,
又因为∠1=∠2,所以∠1+∠4=∠ EOD =90°,
故①正确;
因为∠ AOC =180°-∠ AOB =90°,
所以∠1+∠3=90°.
所以∠3=∠4,故②正确;
因为∠ EOD =90°,
所以∠2+∠3=180°-90°=90°,∠2与∠3不一不相等,
故③错误,④正确.综上,正确的有3个,故选C.
【答案】C
6. [2023·衢州]如图是脊柱侧弯的检测示意图,在体检时为方
便测出 Cobb 角∠ O 的大小,需将∠ O 转化为与它相等的
角,则图中与∠ O 相等的角是( B )
A. ∠ BEA B. ∠ DEB
C. ∠ ECA D. ∠ ADO
B
7. 如图,∠ AOB =120°, OF 平分∠ AOB ,2∠1=∠2.
(1)∠1与∠2互余吗?试说明理由.
【解】∠1与∠2互余.理由如下:
因为∠ AOB =120°, OF 平分∠ AOB ,
所以∠2= ∠ AOB =60°.
因为2∠1=∠2,所以∠1=30°.
所以∠1+∠2=90°,即∠1与∠2互余.
(2)∠2与∠ AOB 互补吗?试说明理由.
【解】∠2与∠ AOB 互补.理由如下:
因为∠2+∠ AOB =60°+120°=180°,
所以∠2与∠ AOB 互补.
易错点 对余角和补角的定义理解不透彻而致错
8. 下列说法中,正确的有 .(填序号)
①钝角与锐角互补;
②∠α的余角是90°-∠α;
③∠β的补角是180°-∠β;
④若∠1+∠2+∠3=90°,则∠1,∠2,∠3互余.
②③
分层练习-巩固
利用余角、补角的定义找图中互为余角、补角的角
9. 如图,点 A , O , B 在同一条直线上,∠ AOD =∠ BOD
=∠ EOC =90°,∠ BOC ∶∠ AOE =3∶1.
(1)求∠ COD 的度数.
【解】由点 A , O , B 在同一条直线
上得∠ AOB =180°.
因为∠ EOC =90°,
所以∠ AOE +∠ BOC =180°-90°=90°.
又因为∠ BOC ∶∠ AOE =3∶1,
所以∠ BOC =90°× =67.5°.
所以∠ COD =∠ BOD -∠ BOC
=90°-67.5°=22.5°.
(2)图中有哪几对角互为余角?
【解】∠ AOE 与∠ DOE ,
∠ AOE 与∠ BOC ,
∠ DOE 与∠ DOC ,
∠ DOC 与∠ BOC ,这4对角互为余角.
(3)图中有哪几对角互为补角?
【解】∠ AOE 与∠ EOB ,
∠ AOD 与∠ DOB ,∠ AOC 与∠ BOC ,
∠ EOD 与∠ AOC ,∠ DOC 与∠ EOB ,
∠ AOD 与∠ EOC ,∠ BOD 与∠ EOC ,
这7对角互为补角.
分层练习-拓展
利用角的运算探求折叠中角的关系
10. [新考法 折叠法]如图,把一张长方形纸片的一角任意折
向长方形内,使点 B 落在点B'的位置,折痕为 EF ;再沿
GF 折叠,使点 C 落在点C'的位置,点 D 落在D'的位置,
如果C'F与FB'在同一条直线上.
(1)分别写出∠1与∠ CFE 、∠2与∠ BFG 之间所满足的
数量关系.
【解】∠1+∠ CFE =180°,∠2+∠ BFG =180°.
(2)写出∠1与∠2之间的数量关系.
【解】∠1=90°-∠2.(或∠1+∠2
=90°或∠2=90°-∠1)
(3)∠ EFG 是什么角?
【解】∠ EFG 是直角.
利用角互余、互补关系探究角的关系
11. [新考法 探究比较法]如图①,∠ AOB =∠ COD =90°.
(1)若∠ BOC =2∠ AOC ,求∠ BOC 的大小.
【解】因为∠ AOB =90°,
所以∠ BOC +∠ AOC =90°.
因为∠ BOC =2∠ AOC ,所以∠ BOC =60°.
(2)试探究∠ BOC 与∠ AOD 之间的数量关系.
【解】因为∠ COD =90°,
所以∠ AOD =∠ COD +∠ AOC =90°+∠ AOC .
因为∠ AOB =90°,
所以∠ BOC +∠ AOC =90°.
所以∠ BOC +∠ AOD =∠ BOC +90°+∠ AOC =
90°+90°=180°,
即∠ BOC +∠ AOD =180°.
(3)若把图①中∠ AOB 绕点 O 旋转到图②的位置,(2)中∠ BOC 与∠ AOD 之间的数量关系还成立吗?试说明理由.
【解】成立.理由:因为∠ AOB =∠ COD =90°,
所以∠ AOB +∠ COD =180°.
因为∠ BOC +∠ AOD +∠ AOB +∠ COD =360°,
所以∠ BOC +∠ AOD =180°.
课堂小结
互 余 互 补
数量 关系
对 应 图 形
性 质
∠1+∠2=90°
∠3+∠4=180°
同角或等角的余角相等
同角或等角的补角相等
同课章节目录
