4.3 用一元一次方程解决问题(第4课时 列表法分析问题 ) 课件(共35张PPT)-七年级数学上册考试满分全攻略同步备课备考系列(苏科版2024)
文档属性
| 名称 | 4.3 用一元一次方程解决问题(第4课时 列表法分析问题 ) 课件(共35张PPT)-七年级数学上册考试满分全攻略同步备课备考系列(苏科版2024) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-27 00:00:00 | ||
图片预览









文档简介
(共35张PPT)
苏科版(2024) 七年级数学上册 第四章 一元一次方程
4.3 用一元一次方程解决问题
第四课时 列表法分析问题
目录/CONTENTS
新知探究
情景导入
学习目标
课堂反馈
分层练习
课堂小结
学习目标
能利用表格或圆形示意图作为建模策略,分析问题中的数量关系列方程解决问题;
进一步体会运用方程解决问题的关键是寻找等量关系,提高分析问题、解决问题的能力.
复习导入
一般 步骤 (1)审题;(2)找等量关系;(3)设未知数;(4)列方程;(5)解所列方程;(6)检验未知数的值是否符合题意; (7)根据问题的需要写出答案
审题 方法 “一读,二划,三复述,四表示.”“一读”就是读题,初步感知题意;“二划”就是在题目上面划符号,找出重点词句, 理出脉络,使题目简单明了;“三复述”就是复述题意,使题目变得详细,题意清晰;“四表示”就是画图表示题意, 使题目变得一目了然
列一元一次方程解决问题
续表:
设未知数 的方法 (1)直接设法:题目问什么,就设什么,它一般适用于要求的未知量只有一个的情况;
(2)间接设法:当直接设元列方程较复杂或较困难时,可选取一个与所求的未知量密切相关的量为未知数,再通过这个未知数求出题目中要求的量;
(3)辅助设法:当题目中的数量关系较复杂或已知条件较少时,为了分析更方便,列方程更容易,在设出所求的未知数的同时,还增设辅助未知数,解方程时不必求出,可在解题时自动消去,即设而不求
特别解读
1. 解题步骤为:审、找、设、列、解、验、答.
2. 审题方法简述为:“一读,二划,三复述,四表示.”
课本例题
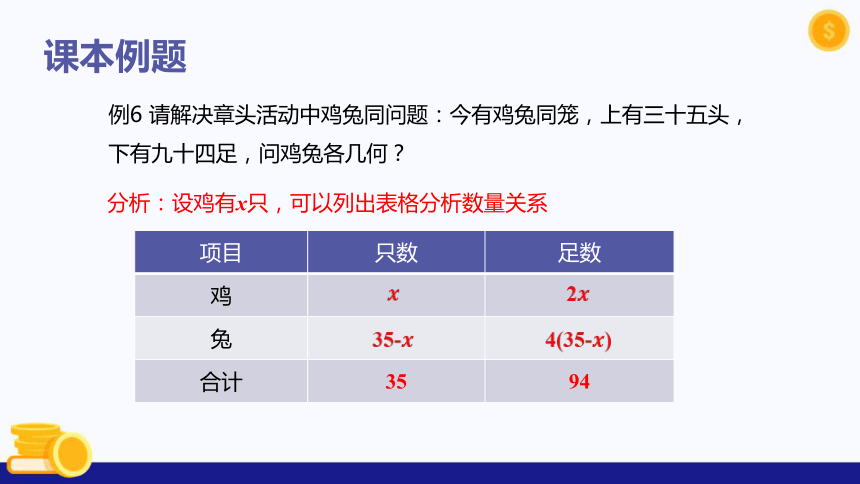
例6 请解决章头活动中鸡兔同问题:今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?
分析:设鸡有x只,可以列出表格分析数量关系
项目 只数 足数
鸡
兔
合计 35 94
2
35-
4(35-)
解:设鸡有只
根据题意,得 2+4(35-)=94
解这个方程,得 =23
35-=12
答:鸡有23只,兔有12只。
课本例题
例7 用计算机处理一批数据,甲单独做需18h完成,乙单独做需12h完成.现在先由甲单独做8h,剩下的部分由甲、乙合作完成,甲、乙两人合作了多长时间?
分析:这个问题中的等量关系: 全部工作量=甲单独做的工作量+甲、乙合做的工作量.全部工作量虽然未知,但可以把它看作一个整体,记作1,那么甲单独做1h完成全部工作量的,乙单独做1h完成全部工作量的.设甲、乙两 人合做了xh,可以列出表格分析数量关系:
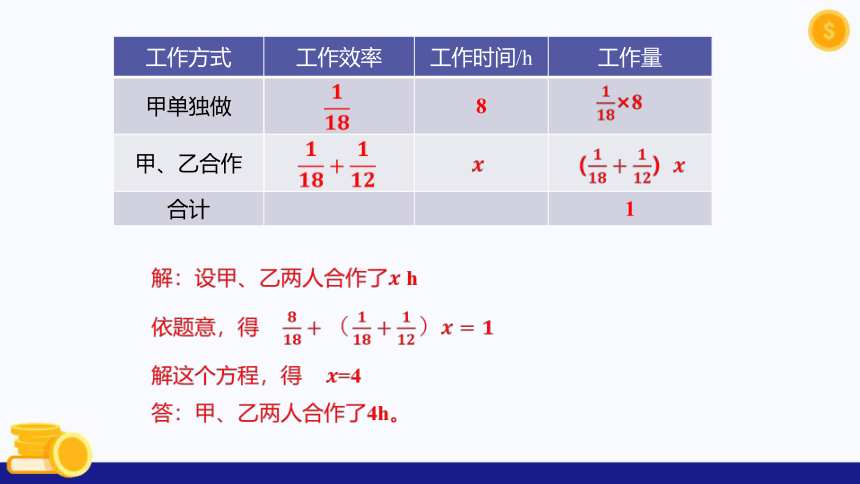
工作方式 工作效率 工作时间/h 工作量
甲单独做 8
甲、乙合作
合计 1
×8
()
解:设甲、乙两人合作了 h
依题意,得
解这个方程,得 =4
答:甲、乙两人合作了4h。
讨 论
解例7时,小明列出的方程是,小丽列出的方程是.你能说明这两个方程的意义吗
用一元一次方程解决问题的关键是找出实际问题中含未知数的等量关系,列表、画示意图等是分析实际问题中数量关系的常用策略 .
解:第一个方程:甲做的工作量十乙做的工作量=1.
第二个方程:甲、乙合做的工作量=1-甲单独做的工作量.
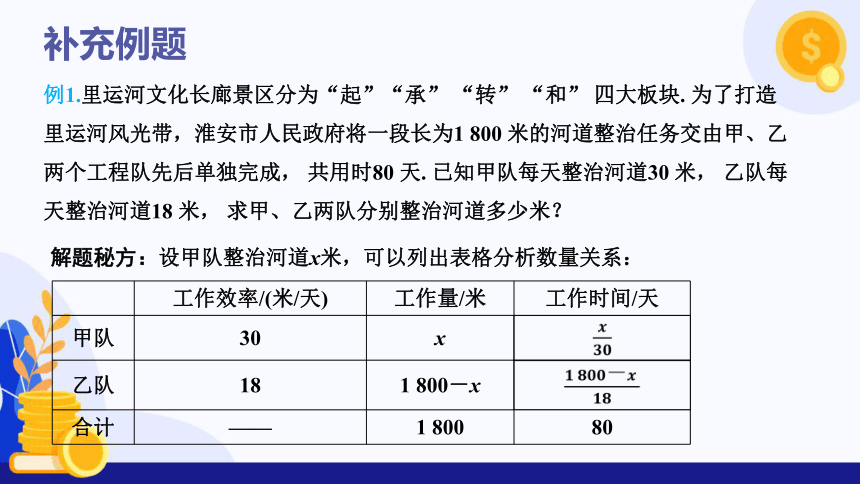
例1.里运河文化长廊景区分为“起”“承” “转” “和” 四大板块. 为了打造里运河风光带,淮安市人民政府将一段长为1 800 米的河道整治任务交由甲、乙两个工程队先后单独完成, 共用时80 天. 已知甲队每天整治河道30 米, 乙队每天整治河道18 米, 求甲、乙两队分别整治河道多少米?
补充例题
解题秘方:设甲队整治河道x米,可以列出表格分析数量关系:
工作效率/(米/天) 工作量/米 工作时间/天
甲队 30 x
乙队 18 1 800-x
合计 —— 1 800 80
解:设甲队整治河道x米,则乙队整治河道(1 800-x)米.
根据题意,得+=80.
解这个方程,得x=900. 则1 800-x=900.
答:甲队整治河道900米,乙队整治河道900米.
补充例题
例1.里运河文化长廊景区分为“起”“承” “转” “和” 四大板块. 为了打造里运河风光带,淮安市人民政府将一段长为1 800 米的河道整治任务交由甲、乙两个工程队先后单独完成, 共用时80 天. 已知甲队每天整治河道30 米, 乙队每天整治河道18 米, 求甲、乙两队分别整治河道多少米?
例2.检查一处住宅区的自来水管,甲单独完成需14 天, 乙单独完成需 18 天, 丙单独完成需 12天, 前7 天由甲、乙两人合作, 但乙中途离开了一段时间, 后2 天由乙、丙两人合作完成, 问乙中途离开了几天?
补充例题
解题秘方:设乙中途离开了x天,可以列出表格分析数量关系:
工作方式 工作效率 工作时间/天 工作量
甲、乙合作 甲 7 ×7
乙 7-x ×(7-x)
乙、丙合作 + 2 (+)×2
合计 —— —— 1
解:设乙中途离开了x天.
根据题意,得×7+×(7-x)+(+)×2=1 ,
解得x=3 .
答: 乙中途离开了3天.
补充例题
例2.检查一处住宅区的自来水管,甲单独完成需14 天, 乙单独完成需 18 天, 丙单独完成需 12天, 前7 天由甲、乙两人合作, 但乙中途离开了一段时间, 后2 天由乙、丙两人合作完成, 问乙中途离开了几天?
方法点拨
1.当工作总量未知时,一般把工作总量看作整体1,则工作效率为单独完成工作总量的时间的倒数.
2. 若将工作总量分几部分完成,则常见的等量关系为各部分的工作量之和等于工作总量.
例3.我国古代数学名著《张丘建算经》中记载: “今有清酒一斗直粟八斗, 醑(xǔ)酒一斗直粟二斗, 今持粟两斛, 得酒四斗, 问清、醑酒各几何?” 大意:现在一斗清酒价值8 斗谷子, 一斗醑酒价值2 斗谷子, 现在拿20 斗谷子, 共换了4 斗酒, 问清酒、醑酒各几斗?
补充例题
解题秘方:设清酒有x斗,可以列出表格分析数量关系:
单价/斗谷子 数量/斗 总价/斗谷子
清酒 8 x 8x
醑酒 2 4-x 2(4-x)
合计 —— 4 20
解:设清酒有x斗,则醑酒有(4-x)斗.
根据题意,得8x+2(4-x)=20,
解这个方程,得x=2 ,则4-x=2 .
答:清酒2斗,醑酒2斗.
补充例题
例3.我国古代数学名著《张丘建算经》中记载: “今有清酒一斗直粟八斗, 醑(xǔ)酒一斗直粟二斗, 今持粟两斛, 得酒四斗, 问清、醑酒各几何?” 大意:现在一斗清酒价值8 斗谷子, 一斗醑酒价值2 斗谷子, 现在拿20 斗谷子, 共换了4 斗酒, 问清酒、醑酒各几斗?
解题技巧
本类题取材于中国古代数学名著《九章算术》、《孙子算经》等,解答此类问题的一般策略:
(1)理解古代语言的含义,把古文转化为现代语言;
(2)紧扣古文中的数量关系,设出未知数,寻找等量关系,列出方程解决问题.
课堂练习
1. 运动会上,小强在200m决赛中先以6m/s的平均速度跑完了大部分赛程,最后以8m/s的平均速度冲刺到达终点,成绩为30s.小强在冲刺阶段花了多少秒?
分析:设小强在冲刺阶段花了秒
跑步阶段 速度 时间 路程
开始 6
冲刺 8
合计 200
30-
6(30-)
8
解:设小强在冲刺阶段花了秒
6(30-)+8=200
解得: =10
答:小强在冲刺阶段花了10秒。
2. 《九章算术》中有一个问题:“今有凫起南海,七日至北海;雁起北海,九日至南海。今凫雁俱起,问何日相逢?”(凫:野鸭。所提问题即“野鸭和大雁从南海和北海同时起飞,经过多少天能够相遇?”)请你解决这个问题。
分析:设经过天相遇
速度 路程
野鸭
大雁
合计 1
解:设经过天相遇
解得: =
答:经过天相遇。
3. 某下水管道工程由甲、乙两个工程队单独铺设分别需要10天、15天完成。现在先由两队从两端同时施工2天,然后由乙队单独施工完成,乙队还需要多少天?
分析:设乙队还需要天
工作方式 效率 时间 工作量
甲、乙合作 2 ()×2
乙队单独施工
合计 1
解:设乙队还需要天
()×2+=1
解得:=10
答:乙队还需要10天。
分层练习-基础
1. [2024 无锡江阴市校级月考]某工程,甲单独做需12天完
成,乙单独做需8天完成,该工程要在规定时间内完成,
现由甲先做3天,乙再参与进来,正好如期完成,求完成
这项工程规定的时间.设完成此项工程规定的时间为 x
天,则下列方程正确的是( A )
A. + =1 B. + =1
C. + =1 D. + =1
A
2. 【新考向·数学文化 2024·盐城期末】我国古代《孙子算经》中记载了这样一个数学问题:“今有三人共车,二车空;二人共车,九人步.问车有几何?”意思是:每3人共乘一辆车,最终剩余2辆车;每2人共乘一辆车,最终有9人无车可乘,问车有多少辆?则车有 辆.
15
3. 某商店采购了一批节能灯,每盏灯20元,在运输过程中损坏了2盏,然后以每盏25元售完,共获利150元,则该商店共进了 盏节能灯.
40
4. 【母题 教材P129例7】一项工程,由甲队单独做需12个月完工,由乙队单独做需15个月完工.现决定由两队合作,且为了加快进度,甲、乙两队都将提高工作效率.若甲队的工作效率提高40%,乙队的工作效率提高25%,则两队合作,几个月可以完工?
解:设两队合作, x 个月可以完工,根据题意,得
x =1,
解得 x =5.
答:两队合作,5个月可以完工.
5. 【新考法·方程建模法】一天晚上停电了,小明同时点上两支粗细不同的蜡烛看书,若干分钟后,来电了,小明将两支蜡烛同时熄灭,已知一支粗蜡烛4小时燃尽,一支细蜡烛3小时燃尽,开始时两根蜡烛一样长,熄灭时粗蜡烛的高度是细蜡烛的2倍,求停电多少分钟.
解:设停电 x 分钟,根据题意,得
1- x =2 ,解得 x =144.
答:停电144分钟.
分层练习-巩固
6. [2024 镇江润州区校级月考]某建筑工地计划租用甲、乙两辆车清理建筑垃圾,已知甲车单独运完需要15天,乙车单独运完需要30天.甲车先单独运了3天,然后甲、乙两车合作运完剩下的垃圾.
(1)甲、乙两车合作还需要多少天运完垃圾?
解:(1)设甲、乙两车合作还需要 x 天运完垃圾,根据
题意,得 + =1,解得 x =8.
答:甲、乙两车合作还需要8天运完垃圾.
(2) 已知甲车每天的租金比乙车多100元,运完垃圾后建筑工地共需支付租金3 950元.则甲、乙两车每天的租金分别为多少元?
解:(2)设乙车每天的租金为 y 元,
则甲车每天的租金为( y +100)元,
根据题意,得(8+3)( y +100)+8 y =3 950,
解得 y =150.
所以 y +100=250.
答:甲车每天的租金为250元,乙车每天的租金为150元.
7. 某市自来水公司为限制单位用水,每月只给某单位计划内用水300吨,计划内用水每吨收费3.5元,超计划部分每吨按4.8元收费.
(1)用代数式表示(所填结果需化简):设用水量为 x 吨,当
用水量小于或等于300吨时,需付款 元;当用
水量大于300吨时,需付款 元.
3.5 x
(4.8 x -390)
(2)该单位4月份缴纳水费1 530元,则该单位4月份用水多少吨?
解:因为300×3.5=1 050(元)<1 530元,
所以该单位4月份用水量大于300吨.
设该单位4月份用水 y 吨,根据题意,得
4.8 y -390=1 530,解得 y =400.
答:该单位4月份用水400吨.
分层练习-拓展
8. [2024 苏州姑苏区校级期末]有甲、乙两工程队对某一小区进行小区改造,甲工程队单独完成这项工程需要20天,乙工程队单独完成这项工程所需的时间比甲工程队多10天.
(1)现在若由甲工程队先单独做5天,剩余部分再由甲、乙两工程队合作,还需要多少天才能完成?
解:(1)由题意可得,乙工程队单独完成这项工程需要
20+10=30(天).
设还需要 x 天才能完成,根据题意,得 + =1,
解得 x =9.
答:还需要9天才能完成.
(2) 已知甲工程队每天施工费用为4 000元,乙工程队每天施工费用为2 000元,若该工程政府拨款70 000元且全部用完,则甲、乙两工程队各需要施工多少天?
解:(2)设甲工程队需要施工 y 天,
则乙工程队需要施工 = 天,
根据题意,得4 000 y +2 000 =70 000,
解得 y =10.则乙工程队需要施工30- ×10=15(天).
答:甲工程队需要施工10天,乙工程队需要施工15天.
课堂小结
用表格分析问题中的数量关系
若要解决的问题比较复杂,为了更好地梳理问题中的数量关系,可以用列表的方法分析问题,找出相等关系.
[说明] 因为表格比较直观、明了,所以在列方程解应用题时经常借助表格反映问题中的量与量之间的关系.
苏科版(2024) 七年级数学上册 第四章 一元一次方程
4.3 用一元一次方程解决问题
第四课时 列表法分析问题
目录/CONTENTS
新知探究
情景导入
学习目标
课堂反馈
分层练习
课堂小结
学习目标
能利用表格或圆形示意图作为建模策略,分析问题中的数量关系列方程解决问题;
进一步体会运用方程解决问题的关键是寻找等量关系,提高分析问题、解决问题的能力.
复习导入
一般 步骤 (1)审题;(2)找等量关系;(3)设未知数;(4)列方程;(5)解所列方程;(6)检验未知数的值是否符合题意; (7)根据问题的需要写出答案
审题 方法 “一读,二划,三复述,四表示.”“一读”就是读题,初步感知题意;“二划”就是在题目上面划符号,找出重点词句, 理出脉络,使题目简单明了;“三复述”就是复述题意,使题目变得详细,题意清晰;“四表示”就是画图表示题意, 使题目变得一目了然
列一元一次方程解决问题
续表:
设未知数 的方法 (1)直接设法:题目问什么,就设什么,它一般适用于要求的未知量只有一个的情况;
(2)间接设法:当直接设元列方程较复杂或较困难时,可选取一个与所求的未知量密切相关的量为未知数,再通过这个未知数求出题目中要求的量;
(3)辅助设法:当题目中的数量关系较复杂或已知条件较少时,为了分析更方便,列方程更容易,在设出所求的未知数的同时,还增设辅助未知数,解方程时不必求出,可在解题时自动消去,即设而不求
特别解读
1. 解题步骤为:审、找、设、列、解、验、答.
2. 审题方法简述为:“一读,二划,三复述,四表示.”
课本例题
例6 请解决章头活动中鸡兔同问题:今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?
分析:设鸡有x只,可以列出表格分析数量关系
项目 只数 足数
鸡
兔
合计 35 94
2
35-
4(35-)
解:设鸡有只
根据题意,得 2+4(35-)=94
解这个方程,得 =23
35-=12
答:鸡有23只,兔有12只。
课本例题
例7 用计算机处理一批数据,甲单独做需18h完成,乙单独做需12h完成.现在先由甲单独做8h,剩下的部分由甲、乙合作完成,甲、乙两人合作了多长时间?
分析:这个问题中的等量关系: 全部工作量=甲单独做的工作量+甲、乙合做的工作量.全部工作量虽然未知,但可以把它看作一个整体,记作1,那么甲单独做1h完成全部工作量的,乙单独做1h完成全部工作量的.设甲、乙两 人合做了xh,可以列出表格分析数量关系:
工作方式 工作效率 工作时间/h 工作量
甲单独做 8
甲、乙合作
合计 1
×8
()
解:设甲、乙两人合作了 h
依题意,得
解这个方程,得 =4
答:甲、乙两人合作了4h。
讨 论
解例7时,小明列出的方程是,小丽列出的方程是.你能说明这两个方程的意义吗
用一元一次方程解决问题的关键是找出实际问题中含未知数的等量关系,列表、画示意图等是分析实际问题中数量关系的常用策略 .
解:第一个方程:甲做的工作量十乙做的工作量=1.
第二个方程:甲、乙合做的工作量=1-甲单独做的工作量.
例1.里运河文化长廊景区分为“起”“承” “转” “和” 四大板块. 为了打造里运河风光带,淮安市人民政府将一段长为1 800 米的河道整治任务交由甲、乙两个工程队先后单独完成, 共用时80 天. 已知甲队每天整治河道30 米, 乙队每天整治河道18 米, 求甲、乙两队分别整治河道多少米?
补充例题
解题秘方:设甲队整治河道x米,可以列出表格分析数量关系:
工作效率/(米/天) 工作量/米 工作时间/天
甲队 30 x
乙队 18 1 800-x
合计 —— 1 800 80
解:设甲队整治河道x米,则乙队整治河道(1 800-x)米.
根据题意,得+=80.
解这个方程,得x=900. 则1 800-x=900.
答:甲队整治河道900米,乙队整治河道900米.
补充例题
例1.里运河文化长廊景区分为“起”“承” “转” “和” 四大板块. 为了打造里运河风光带,淮安市人民政府将一段长为1 800 米的河道整治任务交由甲、乙两个工程队先后单独完成, 共用时80 天. 已知甲队每天整治河道30 米, 乙队每天整治河道18 米, 求甲、乙两队分别整治河道多少米?
例2.检查一处住宅区的自来水管,甲单独完成需14 天, 乙单独完成需 18 天, 丙单独完成需 12天, 前7 天由甲、乙两人合作, 但乙中途离开了一段时间, 后2 天由乙、丙两人合作完成, 问乙中途离开了几天?
补充例题
解题秘方:设乙中途离开了x天,可以列出表格分析数量关系:
工作方式 工作效率 工作时间/天 工作量
甲、乙合作 甲 7 ×7
乙 7-x ×(7-x)
乙、丙合作 + 2 (+)×2
合计 —— —— 1
解:设乙中途离开了x天.
根据题意,得×7+×(7-x)+(+)×2=1 ,
解得x=3 .
答: 乙中途离开了3天.
补充例题
例2.检查一处住宅区的自来水管,甲单独完成需14 天, 乙单独完成需 18 天, 丙单独完成需 12天, 前7 天由甲、乙两人合作, 但乙中途离开了一段时间, 后2 天由乙、丙两人合作完成, 问乙中途离开了几天?
方法点拨
1.当工作总量未知时,一般把工作总量看作整体1,则工作效率为单独完成工作总量的时间的倒数.
2. 若将工作总量分几部分完成,则常见的等量关系为各部分的工作量之和等于工作总量.
例3.我国古代数学名著《张丘建算经》中记载: “今有清酒一斗直粟八斗, 醑(xǔ)酒一斗直粟二斗, 今持粟两斛, 得酒四斗, 问清、醑酒各几何?” 大意:现在一斗清酒价值8 斗谷子, 一斗醑酒价值2 斗谷子, 现在拿20 斗谷子, 共换了4 斗酒, 问清酒、醑酒各几斗?
补充例题
解题秘方:设清酒有x斗,可以列出表格分析数量关系:
单价/斗谷子 数量/斗 总价/斗谷子
清酒 8 x 8x
醑酒 2 4-x 2(4-x)
合计 —— 4 20
解:设清酒有x斗,则醑酒有(4-x)斗.
根据题意,得8x+2(4-x)=20,
解这个方程,得x=2 ,则4-x=2 .
答:清酒2斗,醑酒2斗.
补充例题
例3.我国古代数学名著《张丘建算经》中记载: “今有清酒一斗直粟八斗, 醑(xǔ)酒一斗直粟二斗, 今持粟两斛, 得酒四斗, 问清、醑酒各几何?” 大意:现在一斗清酒价值8 斗谷子, 一斗醑酒价值2 斗谷子, 现在拿20 斗谷子, 共换了4 斗酒, 问清酒、醑酒各几斗?
解题技巧
本类题取材于中国古代数学名著《九章算术》、《孙子算经》等,解答此类问题的一般策略:
(1)理解古代语言的含义,把古文转化为现代语言;
(2)紧扣古文中的数量关系,设出未知数,寻找等量关系,列出方程解决问题.
课堂练习
1. 运动会上,小强在200m决赛中先以6m/s的平均速度跑完了大部分赛程,最后以8m/s的平均速度冲刺到达终点,成绩为30s.小强在冲刺阶段花了多少秒?
分析:设小强在冲刺阶段花了秒
跑步阶段 速度 时间 路程
开始 6
冲刺 8
合计 200
30-
6(30-)
8
解:设小强在冲刺阶段花了秒
6(30-)+8=200
解得: =10
答:小强在冲刺阶段花了10秒。
2. 《九章算术》中有一个问题:“今有凫起南海,七日至北海;雁起北海,九日至南海。今凫雁俱起,问何日相逢?”(凫:野鸭。所提问题即“野鸭和大雁从南海和北海同时起飞,经过多少天能够相遇?”)请你解决这个问题。
分析:设经过天相遇
速度 路程
野鸭
大雁
合计 1
解:设经过天相遇
解得: =
答:经过天相遇。
3. 某下水管道工程由甲、乙两个工程队单独铺设分别需要10天、15天完成。现在先由两队从两端同时施工2天,然后由乙队单独施工完成,乙队还需要多少天?
分析:设乙队还需要天
工作方式 效率 时间 工作量
甲、乙合作 2 ()×2
乙队单独施工
合计 1
解:设乙队还需要天
()×2+=1
解得:=10
答:乙队还需要10天。
分层练习-基础
1. [2024 无锡江阴市校级月考]某工程,甲单独做需12天完
成,乙单独做需8天完成,该工程要在规定时间内完成,
现由甲先做3天,乙再参与进来,正好如期完成,求完成
这项工程规定的时间.设完成此项工程规定的时间为 x
天,则下列方程正确的是( A )
A. + =1 B. + =1
C. + =1 D. + =1
A
2. 【新考向·数学文化 2024·盐城期末】我国古代《孙子算经》中记载了这样一个数学问题:“今有三人共车,二车空;二人共车,九人步.问车有几何?”意思是:每3人共乘一辆车,最终剩余2辆车;每2人共乘一辆车,最终有9人无车可乘,问车有多少辆?则车有 辆.
15
3. 某商店采购了一批节能灯,每盏灯20元,在运输过程中损坏了2盏,然后以每盏25元售完,共获利150元,则该商店共进了 盏节能灯.
40
4. 【母题 教材P129例7】一项工程,由甲队单独做需12个月完工,由乙队单独做需15个月完工.现决定由两队合作,且为了加快进度,甲、乙两队都将提高工作效率.若甲队的工作效率提高40%,乙队的工作效率提高25%,则两队合作,几个月可以完工?
解:设两队合作, x 个月可以完工,根据题意,得
x =1,
解得 x =5.
答:两队合作,5个月可以完工.
5. 【新考法·方程建模法】一天晚上停电了,小明同时点上两支粗细不同的蜡烛看书,若干分钟后,来电了,小明将两支蜡烛同时熄灭,已知一支粗蜡烛4小时燃尽,一支细蜡烛3小时燃尽,开始时两根蜡烛一样长,熄灭时粗蜡烛的高度是细蜡烛的2倍,求停电多少分钟.
解:设停电 x 分钟,根据题意,得
1- x =2 ,解得 x =144.
答:停电144分钟.
分层练习-巩固
6. [2024 镇江润州区校级月考]某建筑工地计划租用甲、乙两辆车清理建筑垃圾,已知甲车单独运完需要15天,乙车单独运完需要30天.甲车先单独运了3天,然后甲、乙两车合作运完剩下的垃圾.
(1)甲、乙两车合作还需要多少天运完垃圾?
解:(1)设甲、乙两车合作还需要 x 天运完垃圾,根据
题意,得 + =1,解得 x =8.
答:甲、乙两车合作还需要8天运完垃圾.
(2) 已知甲车每天的租金比乙车多100元,运完垃圾后建筑工地共需支付租金3 950元.则甲、乙两车每天的租金分别为多少元?
解:(2)设乙车每天的租金为 y 元,
则甲车每天的租金为( y +100)元,
根据题意,得(8+3)( y +100)+8 y =3 950,
解得 y =150.
所以 y +100=250.
答:甲车每天的租金为250元,乙车每天的租金为150元.
7. 某市自来水公司为限制单位用水,每月只给某单位计划内用水300吨,计划内用水每吨收费3.5元,超计划部分每吨按4.8元收费.
(1)用代数式表示(所填结果需化简):设用水量为 x 吨,当
用水量小于或等于300吨时,需付款 元;当用
水量大于300吨时,需付款 元.
3.5 x
(4.8 x -390)
(2)该单位4月份缴纳水费1 530元,则该单位4月份用水多少吨?
解:因为300×3.5=1 050(元)<1 530元,
所以该单位4月份用水量大于300吨.
设该单位4月份用水 y 吨,根据题意,得
4.8 y -390=1 530,解得 y =400.
答:该单位4月份用水400吨.
分层练习-拓展
8. [2024 苏州姑苏区校级期末]有甲、乙两工程队对某一小区进行小区改造,甲工程队单独完成这项工程需要20天,乙工程队单独完成这项工程所需的时间比甲工程队多10天.
(1)现在若由甲工程队先单独做5天,剩余部分再由甲、乙两工程队合作,还需要多少天才能完成?
解:(1)由题意可得,乙工程队单独完成这项工程需要
20+10=30(天).
设还需要 x 天才能完成,根据题意,得 + =1,
解得 x =9.
答:还需要9天才能完成.
(2) 已知甲工程队每天施工费用为4 000元,乙工程队每天施工费用为2 000元,若该工程政府拨款70 000元且全部用完,则甲、乙两工程队各需要施工多少天?
解:(2)设甲工程队需要施工 y 天,
则乙工程队需要施工 = 天,
根据题意,得4 000 y +2 000 =70 000,
解得 y =10.则乙工程队需要施工30- ×10=15(天).
答:甲工程队需要施工10天,乙工程队需要施工15天.
课堂小结
用表格分析问题中的数量关系
若要解决的问题比较复杂,为了更好地梳理问题中的数量关系,可以用列表的方法分析问题,找出相等关系.
[说明] 因为表格比较直观、明了,所以在列方程解应用题时经常借助表格反映问题中的量与量之间的关系.
同课章节目录
