6.3.1 角的概念 课件(共33张PPT)
文档属性
| 名称 | 6.3.1 角的概念 课件(共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 452.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-29 00:00:00 | ||
图片预览





文档简介
(共33张PPT)
角的概念
情景导入
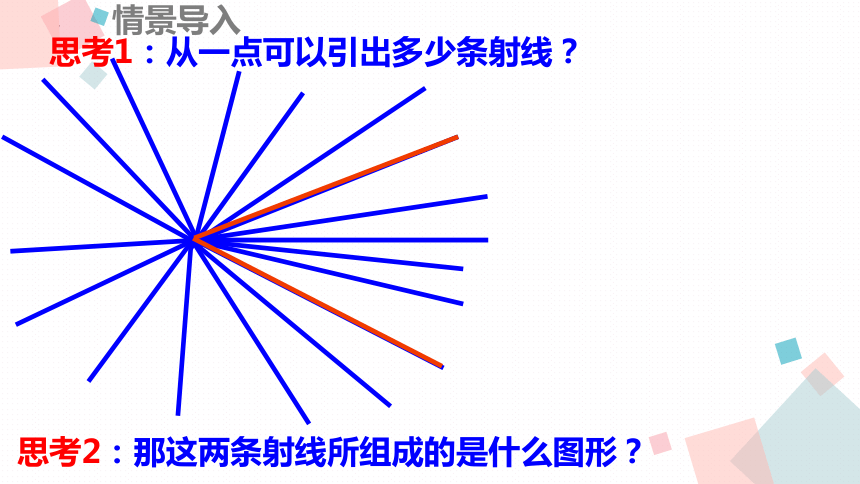
思考1:从一点可以引出多少条射线?
思考2:那这两条射线所组成的是什么图形?
新课讲解
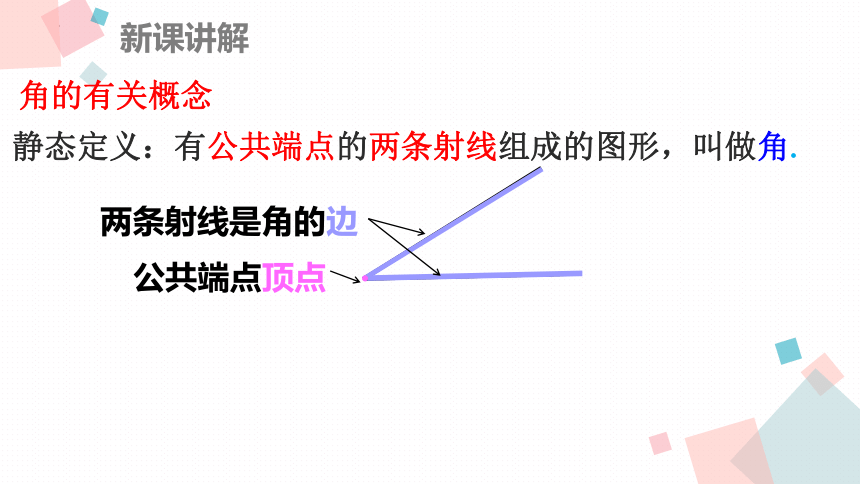
静态定义:有公共端点的两条射线组成的图形,叫做角.
公共端点顶点
两条射线是角的边
角的有关概念
新课讲解
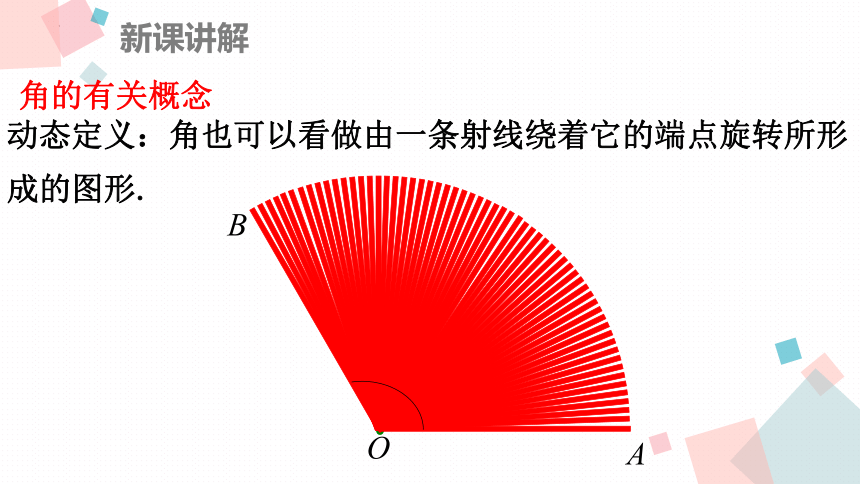
动态定义:角也可以看做由一条射线绕着它的端点旋转所形成的图形.
角的有关概念
A
O
B
新课讲解
O
A
B
B
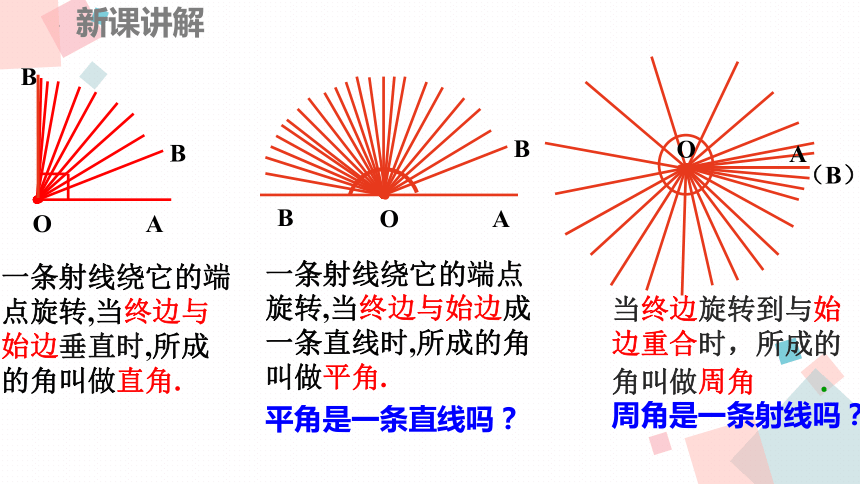
一条射线绕它的端点旋转,当终边与始边垂直时,所成的角叫做直角.
O
A
B
B
一条射线绕它的端点旋转,当终边与始边成一条直线时,所成的角叫做平角.
平角是一条直线吗?
O
A
(B)
当终边旋转到与始边重合时,所成的角叫做周角 .
周角是一条射线吗?
新课讲解
在不做特别说明的情况下,我们说的角都指不大于平角的角
1周角=2平角=4直角=3600
1平角=1800 1直角=900
新知讲解
红角和蓝角到底谁大谁小?
角的大小与边的长短无关!
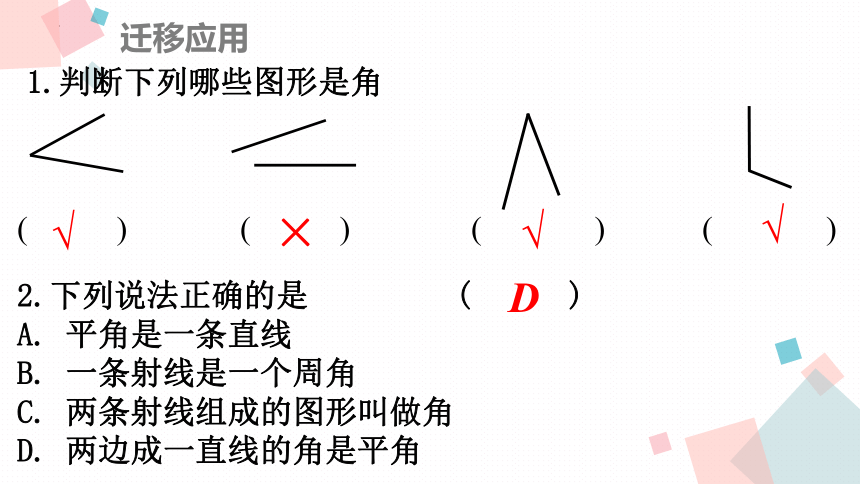
迁移应用
1.判断下列哪些图形是角
( ) ( ) ( ) ( )
√
×
√
√
2.下列说法正确的是 ( )
A. 平角是一条直线
B. 一条射线是一个周角
C. 两条射线组成的图形叫做角
D. 两边成一直线的角是平角
D
迁移应用
1、两条直线组成一个角。 ( )
2、两条射线组成一个角。 ( )
3、具有公共点的两条射线组成一个角 。 ( )
4、角的边画得越长,角就越大。 ( )
5 、两边成一直线的角是平角 ( )
6 、角是由一条射线旋转而成的; ( )
新课讲解
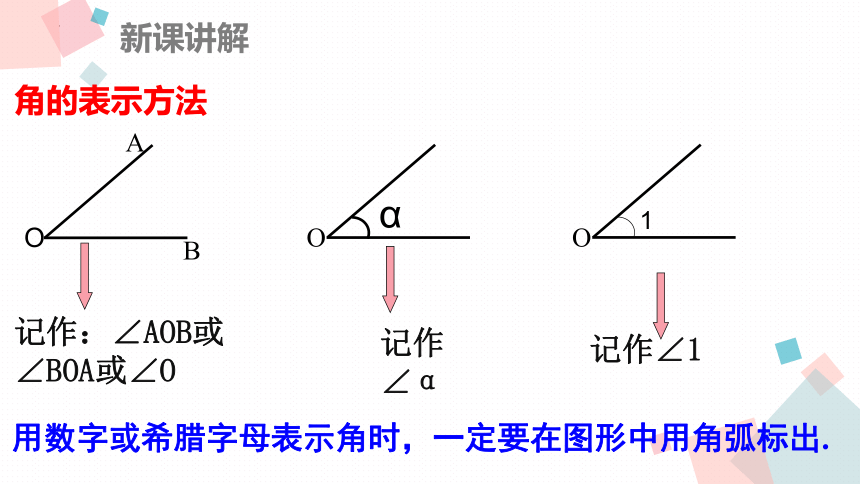
角的表示方法
O
A
B
O
α
O
1
记作:∠AOB或∠BOA或∠O
记作∠α
记作∠1
用数字或希腊字母表示角时,一定要在图形中用角弧标出.
A
B
O
当两个或两个以上的角共同一个顶点时,不能用一个大写字母表示?
C
新课讲解
思考3:下图中有多少个角?
请用正确的方式能把它们表示出来为____________________
∠AOB,∠AOC,∠BOC
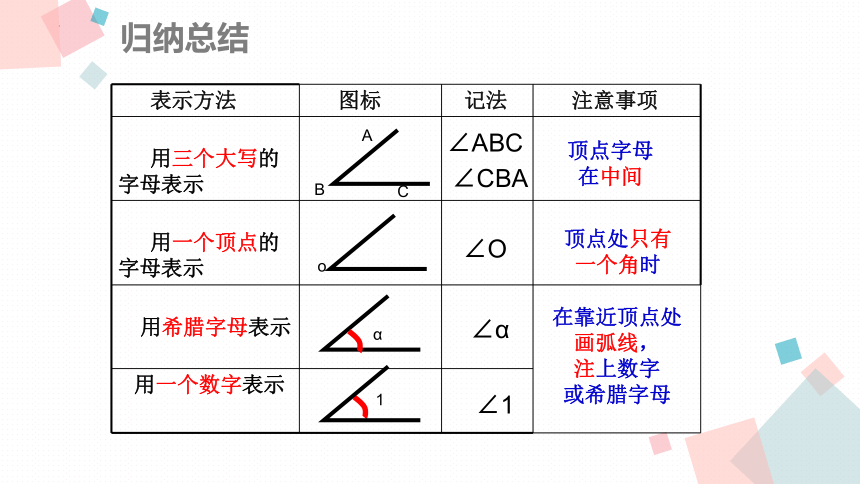
归纳总结
表示方法 图标 记法 注意事项
用三个大写的字母表示
用一个顶点的字母表示
用一个数字表示
C
A
B
o
α
顶点字母
在中间
顶点处只有
一个角时
在靠近顶点处
画弧线,
注上数字
或希腊字母
1
用希腊字母表示
∠ABC
∠CBA
∠O
∠1
∠α
迁移应用
(1)∠1就是∠A;
A
B
D
C
M
1
2
3
(2)∠2就是∠B;
(3)∠3就是∠C .
1:判断下面说法对不对:
P
O
A
C
2:把图中的角表示成下列形式:①∠APO ②∠AOP ③∠OPC,
④∠O ⑤∠COP ⑥∠P。其中正确的有________________ (把你认为正确的序号都填上。)
①③⑥
迁移应用
3. 填写下表,将图中的角用不同方法表示出来.
2
1
3
4
5
B
A
D
C
E
∠1 ∠3 ∠4
∠ACB ∠ABC
∠2
∠BCE
∠BAC
∠BAD
∠5
4.如图所示:(1)图中共有多少个角?请写出能用一个字母表示的角;
(2)把图中所有的角都表示出来.
A
B
C
4
3
2
1
O
解(1)8个;∠A,∠O.
(2)∠A,∠O,∠1,∠2,∠3,∠4, ∠ABC,∠ACB.
新课讲解
怎么知道这个角的大小?
角的度量工具:量角器
角的度量
新课讲解
我们常用量角器量角,度、分、秒是常用的角的度量单位. 把一个周角360等分,每一份就是1度的角,记作1°;把1 度的角60等分,每一份叫做1分的角,记作1′;把1分的角 60等分,每一份叫做1秒的角,记作1″.
1°= ′;1′= ″.
60
60
典例讲解
例1: 用度、分、秒表示:
(1)____________’=______________”
解析:5 =5×60′=300′=300×60″=18000″
(2)____________’=____________”
解析:0.75 =0.75×60′=45′=45×60″=2700″
(3)____________’=_____________”
解析:=×60′=16′=16×60″=960″
45
2700
16
960
300
18000
典例讲解
(4) 57.32°= ° ′ ″;
解析:57.32 =57 +0.32×60′
=57 +19.2′
=57 19′+0.2×60″
=57 19′12″
按1°=60′,1′=60″,先把度化成分,再把分化成秒.
57
19
12
例1: 用度、分、秒表示:
典例讲解
(5)=_________°________’=________”
(6)=________°_________’=________”
(7)=________°_________’=________”
例1: 用度、分、秒表示:
16
14
24
34
22
12
38
9
0
典例讲解
例2.用度表示:
(1)1800″= ′= °
解析:1800″60=30′60=0.5
(2)36″= ′= °
解析:36″60=0.6′60=0.01
(3)48′= °
解析:48′60=0.8
30
0.5
0.6
0.01
0.8
典例讲解
例2.用度表示:
(4) 17°6′36″= °.
17.11
解析:17°6′36″=17°+6′+ ′′
=17°+6.6′
=17 +°
=17.11 .
按1″=′,1′= °先把秒化成分,再把分化成度. (整数化小数)
典例讲解
例2.用度表示:
(5)38°15′= °
(6)27°24′= °
(7)38°36′36″= °
38.25
27.4
38.61
典例讲解
大单位化小单位做乘法
小单位化大单位做除法
问:380 15/ 和38.150 相等吗?
典例讲解
例题3 计算
(1) 12036′56″ + 45024′35″
解:(1)原式=(12+45)0+(36+24)′+(56+35)″
=570+60′+91″
=570+61′+31″
=580+1′+31″
=5801′31″
典例讲解
(2) 79045′- 61048′49″
解:原式=79044′60″- 61048′49″ =780104′60″- 61048′49″
=(78 -61)0(104 -48)′(60-49)″ =17056′11″
典例讲解
(3)21031′27″×3
解:原式=(21×3)0(31×3)′(27×3)″
=63093′81″
=63094′21″
=64034′21″
(4) 63021′39″÷3
解:原式=(63÷3)0(21÷3)′(39÷3)″
=2107′13″
典例讲解
(5)72036′56″-45024′35″
(6)10606′25″÷5
解(5)原式= (72÷45)0(36÷24)′(56÷35)″
= 27012′21″
(6)原式=(106÷5)0(6÷5)′(25÷5)″
=210(66÷5)′(25÷5)″
=21013′(85÷5)″
=21013′17″
拓展探究
1. (1) 如图∠AOB内部画1条射线,问图中一共有多少个角?
A
O
B
答案:3个
(2) 如图∠AOB内部画2条射线,问图中一共有多少个角?
A
O
B
答案:6个
拓展探究
1. (1) 如图∠AOB内部画3条射线,问图中一共有多少个角?
A
O
B
答案:10个
(2) 如图∠AOB内部画4条射线,问图中一共有多少个角?
A
O
B
答案:15个
拓展探究
(5)∠AOB内部画99条射线,问图中一共有多少个角?
答案:5050个
A
O
B
…
(6)∠AOB内部画(n-1)条射线,问图中一共有多少个角?
答案: (1+2+3+…+n)个.
课堂小结
1.本节课你学到了哪些新的数学知识?
2.本节课你有哪些感想?
3.本节课你还有哪些困惑?
布置作业
基础题:1.练习册习题 第 1,2题。
提高题:2.练习册习题第3题
THANK YOU!
感谢聆听
角的概念
情景导入
思考1:从一点可以引出多少条射线?
思考2:那这两条射线所组成的是什么图形?
新课讲解
静态定义:有公共端点的两条射线组成的图形,叫做角.
公共端点顶点
两条射线是角的边
角的有关概念
新课讲解
动态定义:角也可以看做由一条射线绕着它的端点旋转所形成的图形.
角的有关概念
A
O
B
新课讲解
O
A
B
B
一条射线绕它的端点旋转,当终边与始边垂直时,所成的角叫做直角.
O
A
B
B
一条射线绕它的端点旋转,当终边与始边成一条直线时,所成的角叫做平角.
平角是一条直线吗?
O
A
(B)
当终边旋转到与始边重合时,所成的角叫做周角 .
周角是一条射线吗?
新课讲解
在不做特别说明的情况下,我们说的角都指不大于平角的角
1周角=2平角=4直角=3600
1平角=1800 1直角=900
新知讲解
红角和蓝角到底谁大谁小?
角的大小与边的长短无关!
迁移应用
1.判断下列哪些图形是角
( ) ( ) ( ) ( )
√
×
√
√
2.下列说法正确的是 ( )
A. 平角是一条直线
B. 一条射线是一个周角
C. 两条射线组成的图形叫做角
D. 两边成一直线的角是平角
D
迁移应用
1、两条直线组成一个角。 ( )
2、两条射线组成一个角。 ( )
3、具有公共点的两条射线组成一个角 。 ( )
4、角的边画得越长,角就越大。 ( )
5 、两边成一直线的角是平角 ( )
6 、角是由一条射线旋转而成的; ( )
新课讲解
角的表示方法
O
A
B
O
α
O
1
记作:∠AOB或∠BOA或∠O
记作∠α
记作∠1
用数字或希腊字母表示角时,一定要在图形中用角弧标出.
A
B
O
当两个或两个以上的角共同一个顶点时,不能用一个大写字母表示?
C
新课讲解
思考3:下图中有多少个角?
请用正确的方式能把它们表示出来为____________________
∠AOB,∠AOC,∠BOC
归纳总结
表示方法 图标 记法 注意事项
用三个大写的字母表示
用一个顶点的字母表示
用一个数字表示
C
A
B
o
α
顶点字母
在中间
顶点处只有
一个角时
在靠近顶点处
画弧线,
注上数字
或希腊字母
1
用希腊字母表示
∠ABC
∠CBA
∠O
∠1
∠α
迁移应用
(1)∠1就是∠A;
A
B
D
C
M
1
2
3
(2)∠2就是∠B;
(3)∠3就是∠C .
1:判断下面说法对不对:
P
O
A
C
2:把图中的角表示成下列形式:①∠APO ②∠AOP ③∠OPC,
④∠O ⑤∠COP ⑥∠P。其中正确的有________________ (把你认为正确的序号都填上。)
①③⑥
迁移应用
3. 填写下表,将图中的角用不同方法表示出来.
2
1
3
4
5
B
A
D
C
E
∠1 ∠3 ∠4
∠ACB ∠ABC
∠2
∠BCE
∠BAC
∠BAD
∠5
4.如图所示:(1)图中共有多少个角?请写出能用一个字母表示的角;
(2)把图中所有的角都表示出来.
A
B
C
4
3
2
1
O
解(1)8个;∠A,∠O.
(2)∠A,∠O,∠1,∠2,∠3,∠4, ∠ABC,∠ACB.
新课讲解
怎么知道这个角的大小?
角的度量工具:量角器
角的度量
新课讲解
我们常用量角器量角,度、分、秒是常用的角的度量单位. 把一个周角360等分,每一份就是1度的角,记作1°;把1 度的角60等分,每一份叫做1分的角,记作1′;把1分的角 60等分,每一份叫做1秒的角,记作1″.
1°= ′;1′= ″.
60
60
典例讲解
例1: 用度、分、秒表示:
(1)____________’=______________”
解析:5 =5×60′=300′=300×60″=18000″
(2)____________’=____________”
解析:0.75 =0.75×60′=45′=45×60″=2700″
(3)____________’=_____________”
解析:=×60′=16′=16×60″=960″
45
2700
16
960
300
18000
典例讲解
(4) 57.32°= ° ′ ″;
解析:57.32 =57 +0.32×60′
=57 +19.2′
=57 19′+0.2×60″
=57 19′12″
按1°=60′,1′=60″,先把度化成分,再把分化成秒.
57
19
12
例1: 用度、分、秒表示:
典例讲解
(5)=_________°________’=________”
(6)=________°_________’=________”
(7)=________°_________’=________”
例1: 用度、分、秒表示:
16
14
24
34
22
12
38
9
0
典例讲解
例2.用度表示:
(1)1800″= ′= °
解析:1800″60=30′60=0.5
(2)36″= ′= °
解析:36″60=0.6′60=0.01
(3)48′= °
解析:48′60=0.8
30
0.5
0.6
0.01
0.8
典例讲解
例2.用度表示:
(4) 17°6′36″= °.
17.11
解析:17°6′36″=17°+6′+ ′′
=17°+6.6′
=17 +°
=17.11 .
按1″=′,1′= °先把秒化成分,再把分化成度. (整数化小数)
典例讲解
例2.用度表示:
(5)38°15′= °
(6)27°24′= °
(7)38°36′36″= °
38.25
27.4
38.61
典例讲解
大单位化小单位做乘法
小单位化大单位做除法
问:380 15/ 和38.150 相等吗?
典例讲解
例题3 计算
(1) 12036′56″ + 45024′35″
解:(1)原式=(12+45)0+(36+24)′+(56+35)″
=570+60′+91″
=570+61′+31″
=580+1′+31″
=5801′31″
典例讲解
(2) 79045′- 61048′49″
解:原式=79044′60″- 61048′49″ =780104′60″- 61048′49″
=(78 -61)0(104 -48)′(60-49)″ =17056′11″
典例讲解
(3)21031′27″×3
解:原式=(21×3)0(31×3)′(27×3)″
=63093′81″
=63094′21″
=64034′21″
(4) 63021′39″÷3
解:原式=(63÷3)0(21÷3)′(39÷3)″
=2107′13″
典例讲解
(5)72036′56″-45024′35″
(6)10606′25″÷5
解(5)原式= (72÷45)0(36÷24)′(56÷35)″
= 27012′21″
(6)原式=(106÷5)0(6÷5)′(25÷5)″
=210(66÷5)′(25÷5)″
=21013′(85÷5)″
=21013′17″
拓展探究
1. (1) 如图∠AOB内部画1条射线,问图中一共有多少个角?
A
O
B
答案:3个
(2) 如图∠AOB内部画2条射线,问图中一共有多少个角?
A
O
B
答案:6个
拓展探究
1. (1) 如图∠AOB内部画3条射线,问图中一共有多少个角?
A
O
B
答案:10个
(2) 如图∠AOB内部画4条射线,问图中一共有多少个角?
A
O
B
答案:15个
拓展探究
(5)∠AOB内部画99条射线,问图中一共有多少个角?
答案:5050个
A
O
B
…
(6)∠AOB内部画(n-1)条射线,问图中一共有多少个角?
答案: (1+2+3+…+n)个.
课堂小结
1.本节课你学到了哪些新的数学知识?
2.本节课你有哪些感想?
3.本节课你还有哪些困惑?
布置作业
基础题:1.练习册习题 第 1,2题。
提高题:2.练习册习题第3题
THANK YOU!
感谢聆听
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
