14.2 旋转 课件(共35张PPT)
图片预览







文档简介
(共35张PPT)
沪教版(2024)七年级数学上册 第十四章 图形的运动
14.2 旋转
目录/CONTENTS
新知探究
情景导入
学习目标
课堂反馈
分层练习
课堂小结
1. 掌握旋转的有关概念及基本性质;(重点)
2. 能够根据旋转的基本性质解决实际问题.(难点)
学习目标
在日常生活中,我们会遇到图形的转动
情景导入
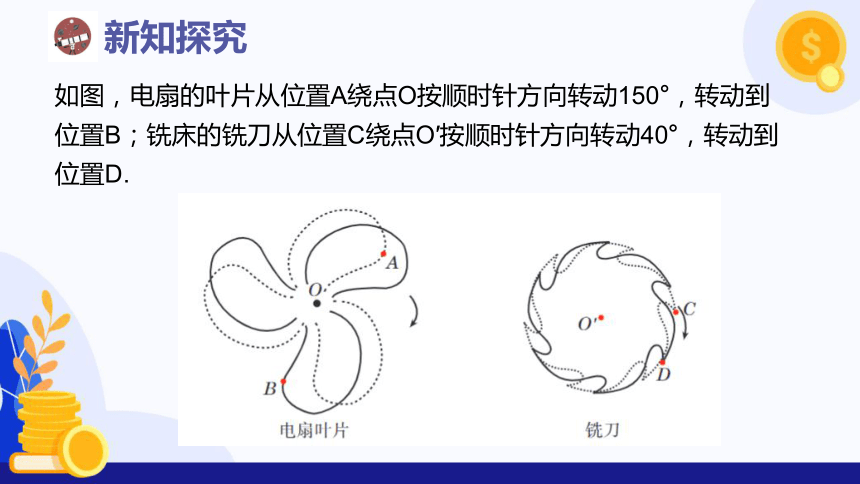
如图,电扇的叶片从位置A绕点O按顺时针方向转动150°,转动到位置B;铣床的铣刀从位置C绕点O′按顺时针方向转动40°,转动到位置D.
新知探究
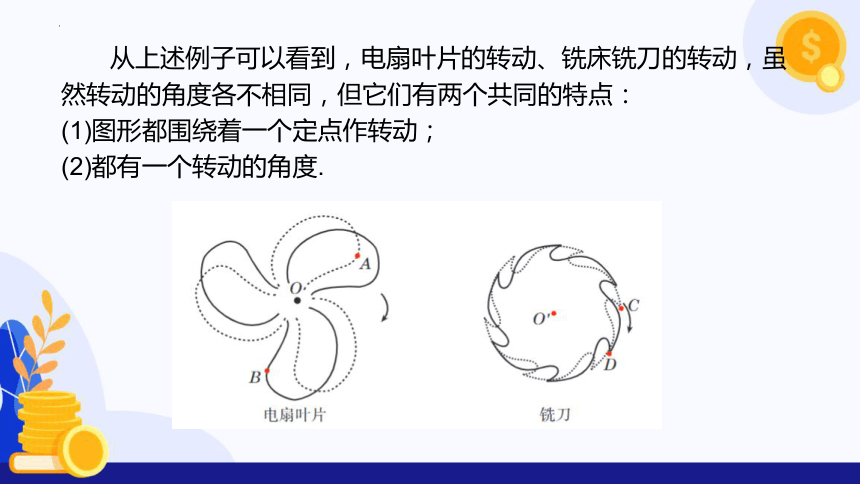
从上述例子可以看到,电扇叶片的转动、铣床铣刀的转动,虽然转动的角度各不相同,但它们有两个共同的特点:
(1)图形都围绕着一个定点作转动;
(2)都有一个转动的角度.
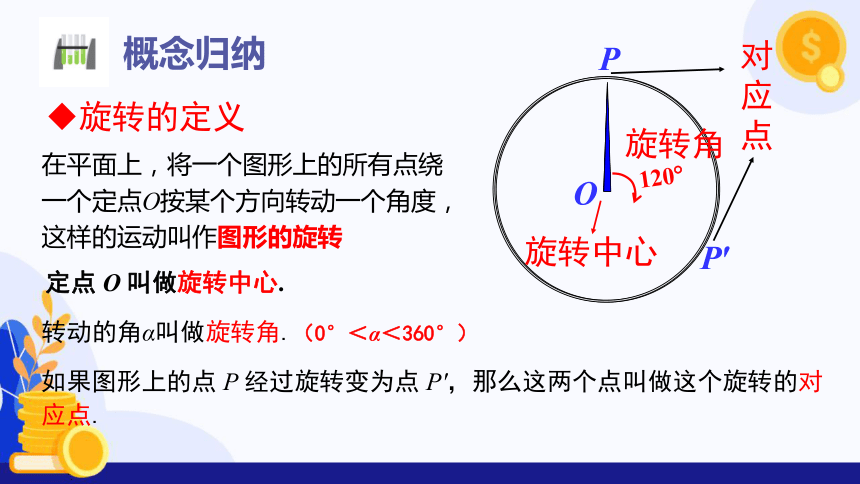
在平面上,将一个图形上的所有点绕一个定点O按某个方向转动一个角度,这样的运动叫作图形的旋转
O
P′
P
旋转中心
旋转角
对应点
旋转的定义
定点 O 叫做旋转中心.
转动的角α叫做旋转角.(0°<α<360°)
如果图形上的点 P 经过旋转变为点 P',那么这两个点叫做这个旋转的对应点.
概念归纳
【练一练】下列物体的运动是旋转的有 .
①电梯的升降运动; ②行驶中的汽车车轮;
③方向盘的转动; ④骑自行车的人;
⑤坐在摩天轮里的小朋友.
②③⑤
方法点拨:判断一种运动是否属于旋转,先看图形是否在同一平面内运动,其次要看是否有旋转中心、旋转角、旋转方向,还要注意判断变化前后图形大小是否发生了变化.
例如,在右图中,三角形ABC绕点O按顺时针方向旋转一个角度成为三角形A1B1C1,点O是旋转中心,∠AOA1是旋转角.在三角形ABC的旋转中,点A与点A1是对应点;线段AB与线段A1B1是对应线段,它们的长度相等;∠BAC与∠B1A1C1是对应角,这两个角的大小也相等.
“某个方向”是指“顺时针方向”或者“逆时针方向”.
图形的旋转具有下列特点:旋转前的图形与旋转后的图形形状相同,大小相等。
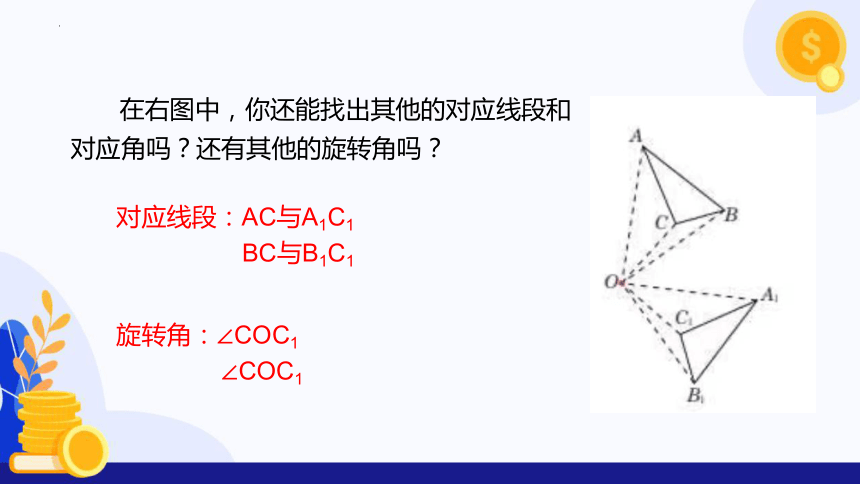
在右图中,你还能找出其他的对应线段和对应角吗?还有其他的旋转角吗?
对应线段:AC与A1C1
BC与B1C1
旋转角:∠COC1
∠COC1
如图14-2-3,将一张正方形纸片两条对角线的公共点上用大头针钉住.旋转正方形,至少旋转几度可以使它与初始位置的正方形重合 每转多少度会重复上述现象
解:旋转正方形,最少旋转90°可以使它与初始位置的正方形重合,每旋转90都会重复上述现象.
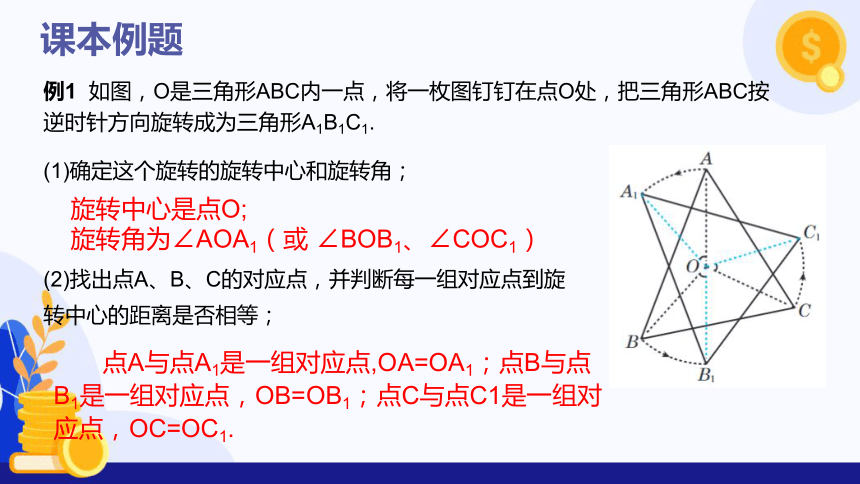
例1 如图,O是三角形ABC内一点,将一枚图钉钉在点O处,把三角形ABC按逆时针方向旋转成为三角形A1B1C1.
(1)确定这个旋转的旋转中心和旋转角;
(2)找出点A、B、C的对应点,并判断每一组对应点到旋转中心的距离是否相等;
旋转中心是点O;
旋转角为∠AOA1(或 ∠BOB1、∠COC1)
点A与点A1是一组对应点,OA=OA1;点B与点B1是一组对应点,OB=OB1;点C与点C1是一组对应点,OC=OC1.
课本例题
例1 如图,O是三角形ABC内一点,将一枚图钉钉在点O处,把三角形ABC按逆时针方向旋转成为三角形A1B1C1.
(3)找出线段AB、BC、AC的对应线段,并判断每一组对应线段是否相等;
(4)找出∠ABC、∠BAC和∠BCA的对应角,并判断每一组对应角是否相等.
线段AB与线段A1B1是一组对应线段,AB=A1B1;线段BC与线段B1C1是一组对应线段,BC=B1C1;线段AC与线段A1C1是一组对应线段,AC=A1C1.
∠ABC与 ∠A1B1C1是一组对应角,∠ABC=∠A1B1C1;∠BAC与∠B1A1C1是一组对应角,∠BAC=∠B1A1C1;∠BCA与∠B1C1A1是一组对应角,∠BCA=∠B1C1A1.
课本例题
90°
如果把图 14-2-4 中的三角形ABC 绕点O按顺时针方向旋转 90°那么线段 OA、OB、OC 旋转的角度是多少
(1)图形旋转后,对应点到旋转中心的距离相等;
(2)两组对应点分别与旋转中心连线,所成的角的角度相等;
(3)对应线段的长度相等,对应角的大小相等;
(4)旋转后得到的图形与原图形形状相同,大小相等.
上面一些例子告诉我们,图形的旋转具有以下性质:
概念归纳
例2 如图,已知点O与三角形ABC,画出三角形ABC绕点O按逆时针方向旋转45°后的图形.
分析 因为图形旋转不改变图形的形状,对图形旋转的画图,关键是要确定表示图形的“关键点”,找出这些点在旋转后的对应点,并按照原图形顺序连接这些对应点.这里,图形三角形ABC的“关键点”是顶点A、B、C,只需画出它们绕点O旋转后的对应点A1、B1、C1,就可得到所求的图形.
课本例题
例2 如图,已知点O与三角形ABC,画出三角形ABC绕点O按逆时针方向旋转45°后的图形.
解:(1)把三角形ABC的顶点A、B、C与旋转中心O连接起来,得到OA、OB、OC.
(3)类似步骤(2)的操作,可分别得到点B、C的对应点B1、C1.
A1
B1
C1
(4)依次连接A1B1、B1C1、C1A1,得到三角A1B1C1.
课本例题
(2)以OA为始边,逆时针方向作45°角,在角的终边上截取OA1,使OA=OA1,得到点A的对应点A1.
(1)如图,点A绕点O按逆时针方向旋转90°后,经过的路线是怎样的图形
A1
(2)如图,线段AB绕点A按顺时针方向旋转45°后,它所扫过的平面部分是怎样的图形?如果AB=3cm,那么这个图形的面积是多少?
S=π(3)2
=3.53cm2
1.画一个直角,并画出这个直角绕它的顶点按逆时针方向旋转120°后的图形.
解:
课堂练习
2.如图,绿色图形绕点O按逆时针方向旋转几度后能与黄色图形重合
解:
180°
课堂练习
3.如图,请作出△ABC绕点O按逆时针方向旋转60°后的图形.
【解析】解:如图,△A′B′C′即为所求.
___
课堂练习
1.在俄罗斯方块游戏中,所有出现的方格体自由下落,如果一行中九个方格齐全,那么这一行会自动消失.已拼好的图案如图所示,现又出现一小方格体,必须进行以下哪项操作,才能拼成一个完整图案,使其全部自动消失( ____ )
A.顺时针旋转90°,向下平移
B.逆时针旋转90°,向下平移
C.顺时针旋转90°,向右平移
D.逆时针旋转90°,向右平移
【解析】解:观察图形可知,出现的小方格需顺时针旋转90°,向右平移至边界.
C
故选:C.
分层练习
2.将图形___绕中心旋转180°后的图形是( ____ )
A.___
B.___
C.___
D.___
【解析】解:将图形绕中心旋转180°,即旋转后的图形与原图形中心对称.
故选:B.
B
3.下列选项中,属于旋转的是( ____ )
A.电梯升降的过程 B.火箭升空的过程
C.雨滴下落的过程 D.幸运大转盘转动的过程
【解析】解:A.电梯升降的过程,是平移现象,故本选项不符合题意;
B.火箭升空的过程,是平移现象,故本选项不符合题意;
C.雨滴下落的过程,是平移现象,故本选项不符合题意;
D.幸运大转盘转动的过程,是旋转现象,故本选项符合题意意.
D
故选:D.
4.下列四个图形中,最贴近“将线段AB绕其端点B顺时针旋转”这个描述的是( ____ )
A._____
B._____
C._____
D._____
B
【解析】解:A、该图形是由线段AB绕其端点B逆时针旋转得到,不合题意;
B、该图形是由线段AB绕其端点B顺时针旋转得到,符合题意;
C、该图形是由射线AB绕其端点B逆时针旋转得到,不合题意;
D、该图形是由射线AB绕其端点B顺时针旋转得到,不合题意;
故选:B.
5.李明家有一个时钟,假期间,某天上午他8点整出门锻炼,回家时发现时针刚好旋转了60°,那么李明回家的时间是( ____ )
A.9点整 B.9点半
C.10点整 D.10点半
【解析】解:由于时针旋转一周(360°)是12小时,则每小时旋转 ,
∴当旋转60°时,李明回家的时间是: (点整),
故选:C.
C
6.一天中钟表时针从上午6时到上午9时旋转的度数为 _____ .
【解析】解:根据题意,从上午6时到上午9时,共3个小时,
∴时针旋转了 圆周,旋转的角度为 .
故答案为:90°.
90°
7.如图,教室内地面有个倾斜的畚箕,箕面AB与水平地面的夹角∠CAB为62°,小明将它扶起(将畚箕绕点A顺时针旋转)后平放在地面,箕面AB绕点A旋转的度数为 ______ .
【解析】解:∵AB与地面的夹角∠CAB为62°,
∴∠BAB'=180°-∠CAB=180°-62°=118°,
即旋转角为118°,
∴箕面AB绕点A旋转的度数为118°.
故答案为:118°.
118°
8.新田孝文化公园,占地11万平方米,集孝德教育、休闲旅游为一体,建有孝文化主题广场、孝文化博物馆、二十四孝故事园、施恩柱等七大景区.图1是孝文化公园游乐场里的摩天轮摩天轮上以等间隔的方式设置36个车厢,车厢依顺时针方向分别编号为1号到36号,且摩天轮运行时以逆时针方向等速旋转,旋转一圈花费30分钟.若图2表示21号车厢运行到最高点的情形,则此时经过 ____ 分钟后,9号车厢才会运行到最高点?
【解析】解: (分钟),
所以经过20分钟后,9号车厢才会运行到最高点.
20
故答案为:20.
9.如图,可以看作是一个弓形通过几次旋转得到的?每次旋转了多少度?
【解析】解:将图形弓形顺时针或(逆时针)旋转3次,每次旋转了90°.
答:可以看作是一个弓形通过3次旋转得到的?每次旋转了90度.
10.钟表的分针匀速旋转一周需要60min.
(1)指出它的旋转中心;
(2)经过20min,分针旋转了多少度?
【解析】解:(1)旋转中心是时针与分针的交点;
(2)∵6°×20=120°.
∴分针转过的角度是120度.
11.如图,小明坐在秋千上,秋千旋转了80°.请在图中小明身上任意选一点P,利用旋转性质,标出点P的对应点.
(1)这两个点到旋转中心的距离有怎样的关系?
(2)这两个点与旋转中心所连线段的夹角是多少度?
【解析】解:如图,P的对应点为P′,旋转中心为点O,连接OP,OP′,
____
(1)根据旋转的性质得OP=OP′;
(2)根据旋转的性质得∠POP′=80°.
12.如图(1)所示,魔术师把4张扑克牌放在桌子上,然后蒙住眼睛,请一位观众上台,把某一张牌旋转180°.魔术师解除蒙具后,看到4张扑克牌如图(2)所示,他很快确定了哪一张牌被旋转过.你能吗?
____________
【解析】解:我能,方法如下:
图(1)与图(2)中扑克牌完全一样,说明被旋转过的牌是中心对称图形,
而图中只有方块4是中心对称图形,故方块4被旋转过.
旋转中心
旋转角
旋转方向
必须明确
确定一次图形的旋转时:
温馨提示:旋转的范围是“平面内”,其中“旋转中心,旋转方向,旋转角度”称为旋转的三要素;
课堂小结
沪教版(2024)七年级数学上册 第十四章 图形的运动
14.2 旋转
目录/CONTENTS
新知探究
情景导入
学习目标
课堂反馈
分层练习
课堂小结
1. 掌握旋转的有关概念及基本性质;(重点)
2. 能够根据旋转的基本性质解决实际问题.(难点)
学习目标
在日常生活中,我们会遇到图形的转动
情景导入
如图,电扇的叶片从位置A绕点O按顺时针方向转动150°,转动到位置B;铣床的铣刀从位置C绕点O′按顺时针方向转动40°,转动到位置D.
新知探究
从上述例子可以看到,电扇叶片的转动、铣床铣刀的转动,虽然转动的角度各不相同,但它们有两个共同的特点:
(1)图形都围绕着一个定点作转动;
(2)都有一个转动的角度.
在平面上,将一个图形上的所有点绕一个定点O按某个方向转动一个角度,这样的运动叫作图形的旋转
O
P′
P
旋转中心
旋转角
对应点
旋转的定义
定点 O 叫做旋转中心.
转动的角α叫做旋转角.(0°<α<360°)
如果图形上的点 P 经过旋转变为点 P',那么这两个点叫做这个旋转的对应点.
概念归纳
【练一练】下列物体的运动是旋转的有 .
①电梯的升降运动; ②行驶中的汽车车轮;
③方向盘的转动; ④骑自行车的人;
⑤坐在摩天轮里的小朋友.
②③⑤
方法点拨:判断一种运动是否属于旋转,先看图形是否在同一平面内运动,其次要看是否有旋转中心、旋转角、旋转方向,还要注意判断变化前后图形大小是否发生了变化.
例如,在右图中,三角形ABC绕点O按顺时针方向旋转一个角度成为三角形A1B1C1,点O是旋转中心,∠AOA1是旋转角.在三角形ABC的旋转中,点A与点A1是对应点;线段AB与线段A1B1是对应线段,它们的长度相等;∠BAC与∠B1A1C1是对应角,这两个角的大小也相等.
“某个方向”是指“顺时针方向”或者“逆时针方向”.
图形的旋转具有下列特点:旋转前的图形与旋转后的图形形状相同,大小相等。
在右图中,你还能找出其他的对应线段和对应角吗?还有其他的旋转角吗?
对应线段:AC与A1C1
BC与B1C1
旋转角:∠COC1
∠COC1
如图14-2-3,将一张正方形纸片两条对角线的公共点上用大头针钉住.旋转正方形,至少旋转几度可以使它与初始位置的正方形重合 每转多少度会重复上述现象
解:旋转正方形,最少旋转90°可以使它与初始位置的正方形重合,每旋转90都会重复上述现象.
例1 如图,O是三角形ABC内一点,将一枚图钉钉在点O处,把三角形ABC按逆时针方向旋转成为三角形A1B1C1.
(1)确定这个旋转的旋转中心和旋转角;
(2)找出点A、B、C的对应点,并判断每一组对应点到旋转中心的距离是否相等;
旋转中心是点O;
旋转角为∠AOA1(或 ∠BOB1、∠COC1)
点A与点A1是一组对应点,OA=OA1;点B与点B1是一组对应点,OB=OB1;点C与点C1是一组对应点,OC=OC1.
课本例题
例1 如图,O是三角形ABC内一点,将一枚图钉钉在点O处,把三角形ABC按逆时针方向旋转成为三角形A1B1C1.
(3)找出线段AB、BC、AC的对应线段,并判断每一组对应线段是否相等;
(4)找出∠ABC、∠BAC和∠BCA的对应角,并判断每一组对应角是否相等.
线段AB与线段A1B1是一组对应线段,AB=A1B1;线段BC与线段B1C1是一组对应线段,BC=B1C1;线段AC与线段A1C1是一组对应线段,AC=A1C1.
∠ABC与 ∠A1B1C1是一组对应角,∠ABC=∠A1B1C1;∠BAC与∠B1A1C1是一组对应角,∠BAC=∠B1A1C1;∠BCA与∠B1C1A1是一组对应角,∠BCA=∠B1C1A1.
课本例题
90°
如果把图 14-2-4 中的三角形ABC 绕点O按顺时针方向旋转 90°那么线段 OA、OB、OC 旋转的角度是多少
(1)图形旋转后,对应点到旋转中心的距离相等;
(2)两组对应点分别与旋转中心连线,所成的角的角度相等;
(3)对应线段的长度相等,对应角的大小相等;
(4)旋转后得到的图形与原图形形状相同,大小相等.
上面一些例子告诉我们,图形的旋转具有以下性质:
概念归纳
例2 如图,已知点O与三角形ABC,画出三角形ABC绕点O按逆时针方向旋转45°后的图形.
分析 因为图形旋转不改变图形的形状,对图形旋转的画图,关键是要确定表示图形的“关键点”,找出这些点在旋转后的对应点,并按照原图形顺序连接这些对应点.这里,图形三角形ABC的“关键点”是顶点A、B、C,只需画出它们绕点O旋转后的对应点A1、B1、C1,就可得到所求的图形.
课本例题
例2 如图,已知点O与三角形ABC,画出三角形ABC绕点O按逆时针方向旋转45°后的图形.
解:(1)把三角形ABC的顶点A、B、C与旋转中心O连接起来,得到OA、OB、OC.
(3)类似步骤(2)的操作,可分别得到点B、C的对应点B1、C1.
A1
B1
C1
(4)依次连接A1B1、B1C1、C1A1,得到三角A1B1C1.
课本例题
(2)以OA为始边,逆时针方向作45°角,在角的终边上截取OA1,使OA=OA1,得到点A的对应点A1.
(1)如图,点A绕点O按逆时针方向旋转90°后,经过的路线是怎样的图形
A1
(2)如图,线段AB绕点A按顺时针方向旋转45°后,它所扫过的平面部分是怎样的图形?如果AB=3cm,那么这个图形的面积是多少?
S=π(3)2
=3.53cm2
1.画一个直角,并画出这个直角绕它的顶点按逆时针方向旋转120°后的图形.
解:
课堂练习
2.如图,绿色图形绕点O按逆时针方向旋转几度后能与黄色图形重合
解:
180°
课堂练习
3.如图,请作出△ABC绕点O按逆时针方向旋转60°后的图形.
【解析】解:如图,△A′B′C′即为所求.
___
课堂练习
1.在俄罗斯方块游戏中,所有出现的方格体自由下落,如果一行中九个方格齐全,那么这一行会自动消失.已拼好的图案如图所示,现又出现一小方格体,必须进行以下哪项操作,才能拼成一个完整图案,使其全部自动消失( ____ )
A.顺时针旋转90°,向下平移
B.逆时针旋转90°,向下平移
C.顺时针旋转90°,向右平移
D.逆时针旋转90°,向右平移
【解析】解:观察图形可知,出现的小方格需顺时针旋转90°,向右平移至边界.
C
故选:C.
分层练习
2.将图形___绕中心旋转180°后的图形是( ____ )
A.___
B.___
C.___
D.___
【解析】解:将图形绕中心旋转180°,即旋转后的图形与原图形中心对称.
故选:B.
B
3.下列选项中,属于旋转的是( ____ )
A.电梯升降的过程 B.火箭升空的过程
C.雨滴下落的过程 D.幸运大转盘转动的过程
【解析】解:A.电梯升降的过程,是平移现象,故本选项不符合题意;
B.火箭升空的过程,是平移现象,故本选项不符合题意;
C.雨滴下落的过程,是平移现象,故本选项不符合题意;
D.幸运大转盘转动的过程,是旋转现象,故本选项符合题意意.
D
故选:D.
4.下列四个图形中,最贴近“将线段AB绕其端点B顺时针旋转”这个描述的是( ____ )
A._____
B._____
C._____
D._____
B
【解析】解:A、该图形是由线段AB绕其端点B逆时针旋转得到,不合题意;
B、该图形是由线段AB绕其端点B顺时针旋转得到,符合题意;
C、该图形是由射线AB绕其端点B逆时针旋转得到,不合题意;
D、该图形是由射线AB绕其端点B顺时针旋转得到,不合题意;
故选:B.
5.李明家有一个时钟,假期间,某天上午他8点整出门锻炼,回家时发现时针刚好旋转了60°,那么李明回家的时间是( ____ )
A.9点整 B.9点半
C.10点整 D.10点半
【解析】解:由于时针旋转一周(360°)是12小时,则每小时旋转 ,
∴当旋转60°时,李明回家的时间是: (点整),
故选:C.
C
6.一天中钟表时针从上午6时到上午9时旋转的度数为 _____ .
【解析】解:根据题意,从上午6时到上午9时,共3个小时,
∴时针旋转了 圆周,旋转的角度为 .
故答案为:90°.
90°
7.如图,教室内地面有个倾斜的畚箕,箕面AB与水平地面的夹角∠CAB为62°,小明将它扶起(将畚箕绕点A顺时针旋转)后平放在地面,箕面AB绕点A旋转的度数为 ______ .
【解析】解:∵AB与地面的夹角∠CAB为62°,
∴∠BAB'=180°-∠CAB=180°-62°=118°,
即旋转角为118°,
∴箕面AB绕点A旋转的度数为118°.
故答案为:118°.
118°
8.新田孝文化公园,占地11万平方米,集孝德教育、休闲旅游为一体,建有孝文化主题广场、孝文化博物馆、二十四孝故事园、施恩柱等七大景区.图1是孝文化公园游乐场里的摩天轮摩天轮上以等间隔的方式设置36个车厢,车厢依顺时针方向分别编号为1号到36号,且摩天轮运行时以逆时针方向等速旋转,旋转一圈花费30分钟.若图2表示21号车厢运行到最高点的情形,则此时经过 ____ 分钟后,9号车厢才会运行到最高点?
【解析】解: (分钟),
所以经过20分钟后,9号车厢才会运行到最高点.
20
故答案为:20.
9.如图,可以看作是一个弓形通过几次旋转得到的?每次旋转了多少度?
【解析】解:将图形弓形顺时针或(逆时针)旋转3次,每次旋转了90°.
答:可以看作是一个弓形通过3次旋转得到的?每次旋转了90度.
10.钟表的分针匀速旋转一周需要60min.
(1)指出它的旋转中心;
(2)经过20min,分针旋转了多少度?
【解析】解:(1)旋转中心是时针与分针的交点;
(2)∵6°×20=120°.
∴分针转过的角度是120度.
11.如图,小明坐在秋千上,秋千旋转了80°.请在图中小明身上任意选一点P,利用旋转性质,标出点P的对应点.
(1)这两个点到旋转中心的距离有怎样的关系?
(2)这两个点与旋转中心所连线段的夹角是多少度?
【解析】解:如图,P的对应点为P′,旋转中心为点O,连接OP,OP′,
____
(1)根据旋转的性质得OP=OP′;
(2)根据旋转的性质得∠POP′=80°.
12.如图(1)所示,魔术师把4张扑克牌放在桌子上,然后蒙住眼睛,请一位观众上台,把某一张牌旋转180°.魔术师解除蒙具后,看到4张扑克牌如图(2)所示,他很快确定了哪一张牌被旋转过.你能吗?
____________
【解析】解:我能,方法如下:
图(1)与图(2)中扑克牌完全一样,说明被旋转过的牌是中心对称图形,
而图中只有方块4是中心对称图形,故方块4被旋转过.
旋转中心
旋转角
旋转方向
必须明确
确定一次图形的旋转时:
温馨提示:旋转的范围是“平面内”,其中“旋转中心,旋转方向,旋转角度”称为旋转的三要素;
课堂小结
同课章节目录
