24.1 旋转(第3课时在平面直角坐标系中对图形进行旋转变换)课件(共51张PPT)
文档属性
| 名称 | 24.1 旋转(第3课时在平面直角坐标系中对图形进行旋转变换)课件(共51张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-29 07:28:22 | ||
图片预览






文档简介
(共51张PPT)
九年级沪科版数学下册 第二十四章 圆
第3课时在平面直角坐标系中对图形进行旋转变换
24.1 旋转
目录/CONTENTS
新知探究
情景导入
学习目标
课堂反馈
分层练习
课堂小结
1. 理解并掌握旋转变化的特点,能够解决坐标平面内的旋转变换问题.(重点、难点)
2. 能够运用旋转、轴对称或平移进行简单的图案设计.(难点)
学习目标
旋转的定义:
在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,得到另一个图形的变换,这样的图形变换称为旋转。
中心对称的定义:
在平面内,将一个图形绕着某一定点旋转180度,得到另一个图形,那么,我们就说这两个图形关于这个点成中心对称。
情景导入
旋转的性质:
1. 旋转不改变图形的大小和形状.
2. 任意一对对应点与旋转中心的连线所成的角相等,都等于旋转角.
3. 对应点到旋转中心的距离相等.
4. 旋转中心是唯一不动的点.
情景导入
中心对称的性质:
关于中心对称的两个图形,对应点所连线段都经过对称中心,并且被对称中心所平分,具有旋转的所有性质.
旋转对称图形:
在平面内,一个图形绕着一个定点旋转一定的角度后,能够与原图_______,这样的图形叫做旋转对称图形,这个定点就是_________.
重合
旋转中心
情景导入
中心对称图形定义:
如果一个图形绕一个点旋转180°后,能和原来的图形互相重合,那么这个图形叫做中心对称图形;这个点叫做它的对称中心.
情景导入
A
B
1
2
2
-1
-2
-2
x
y
O
1
-1
C
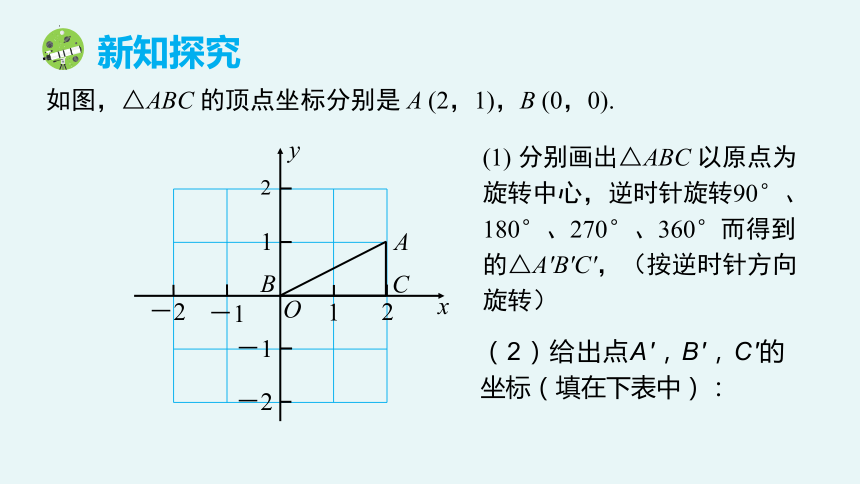
如图,△ABC 的顶点坐标分别是 A (2,1),B (0,0).
(1) 分别画出△ABC 以原点为旋转中心,逆时针旋转90°、180°、270°、360°而得到的△A′B′C′,(按逆时针方向旋转)
新知探究
(2)给出点A′,B′,C′的坐标(填在下表中):
A
B
1
2
2
-1
-2
-2
x
y
O
1
-1
C
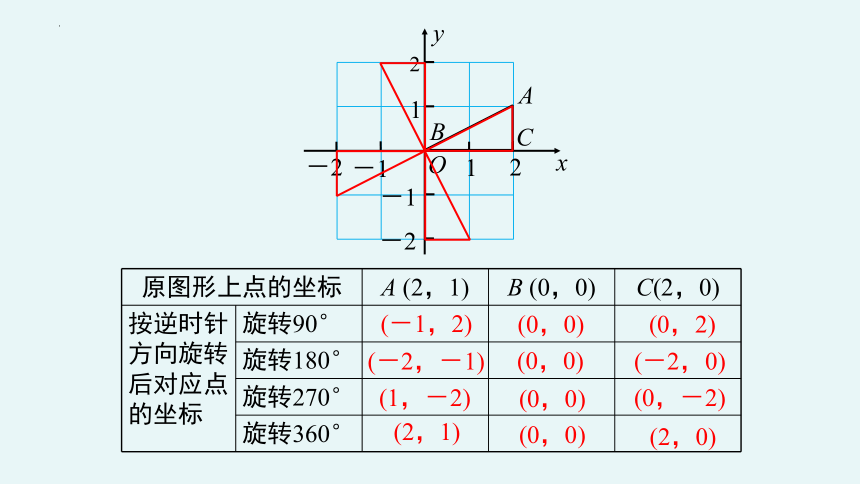
原图形上点的坐标 A (2,1) B (0,0) C(2,0)
按逆时针方向旋转后对应点的坐标 旋转90°
旋转180°
旋转270°
旋转360°
(-1,2)
(-2,-1)
(1,-2)
(2,1)
(0,0)
(0,2)
(0,0)
(0,0)
(0,0)
(-2,0)
(0,-2)
(2,0)
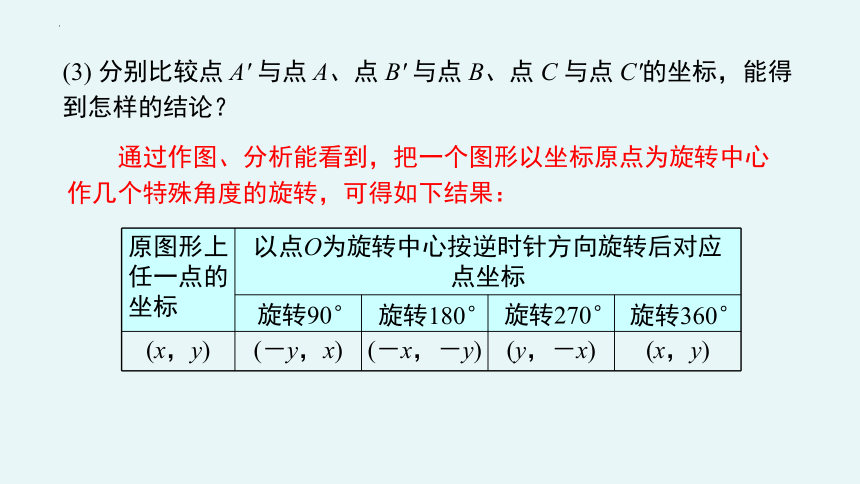
(3) 分别比较点 A′ 与点 A、点 B′ 与点 B、点 C 与点 C′的坐标,能得到怎样的结论?
通过作图、分析能看到,把一个图形以坐标原点为旋转中心作几个特殊角度的旋转,可得如下结果:
原图形上任一点的坐标 以点O为旋转中心按逆时针方向旋转后对应点坐标
(x,y) (-y,x) (-x,-y) (y,-x) (x,y)
旋转90°
旋转180°
旋转270°
旋转360°
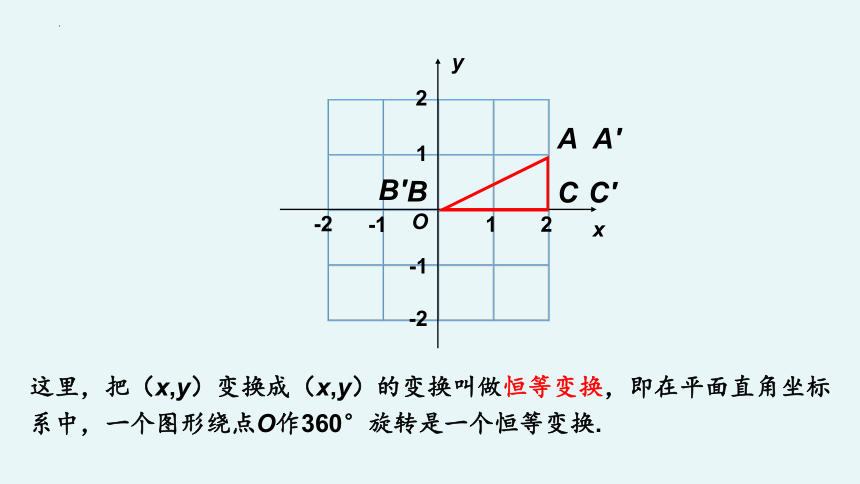
这里,把(x,y)变换成(x,y)的变换叫做恒等变换,即在平面直角坐标系中,一个图形绕点O作360°旋转是一个恒等变换.
x
y
O
1
2
-2
-1
1
2
-2
-1
A
B
C
A′
C′
B′
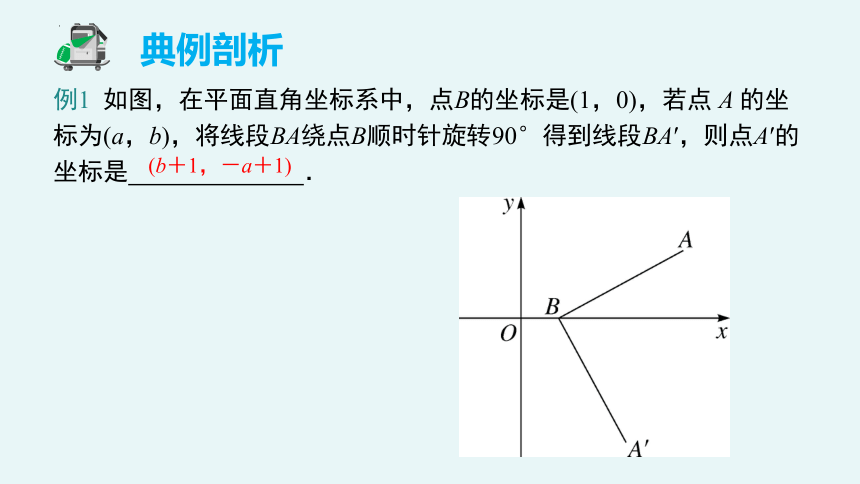
例1 如图,在平面直角坐标系中,点B的坐标是(1,0),若点 A 的坐标为(a,b),将线段BA绕点B顺时针旋转90°得到线段BA′,则点A′的坐标是 .
(b+1,-a+1)
典例剖析
解析:过点 A 作 AC⊥x 轴,过点 A′ 作 A′D ⊥ x 轴,垂足分别为 C、D,显然
Rt △ABC ≌ Rt △BA′D. ∵点 A 的坐标为 (a,b),点 B 的坐标是 (1,0),∴OD=OB+BD=OB+AC=1+b,A′D=BC=OC-OB=a-1. ∵点 A′ 在第四象限,∴点A′的坐标是(b+1,-a+1).故答案为(b+1,-a+1).
试说出构成下列图形的基本图形.
(1)
(2)
(3)
(4)
新知探究
基本图案
图案的形成过程
分析图案的形成过程
基本图案
图案的形成过程
分析图案的形成过程
归纳:图形的变换可以通过选择不同的变换方式得到,可能需要旋转、轴对称、平移等多种变换组合才能得到完美的图案.
例2 用四块如图(1)所示的正方形卡片拼成一个新的正方形,使拼成的图案是一个轴对称图形,请你在图(2)、图(3)、图(4)中各画出一种拼法(要求三种画法各不相同,且其中至少有一个既是轴对称图形,又是中心对称图形).
解:如图所示.(答案不唯一)
典例剖析
例3 如图,是一个4×4的正方形网格,每个小正方形的边长为1.请你在网格中以左上角的三角形为基本图形,通过平移、轴对称或旋转变换,设计一个精美图案,使其满足:①既是轴对称图形,又是以点O为对称中心的中心对称图形;②所作图案用阴影标识,且阴影部分面积为4.
分析:所给左上角的三角形的面积为 1×1÷2=0.5,故设计图案总共需要三角形 4÷0.5=8 (个).
典例剖析
解:答案不唯一,以下图案供参考.
A
分层练习-基础
2. 如图,点A的坐标是(-4,6),将线段OA绕点O顺时针旋转90°,点A的对应点的坐标是( )
A.(4,6) B.(6,4)
C.(-6,-4) D.(-4,-6)
B
D
4.[2024·德州德城区期末]如图,在正方形网格中,线段AB绕一点旋转一定的角度后与线段CD重合(C,D均为格点,点A的对应点是点C),若点A的坐标为(-1,5),点B的坐标为(3,3),则旋转中心的坐标为________.
(1,1)
【点拨】如图,建立平面直角坐标系,连接AC,BD,作AC,BD的垂直平分线交于点E,点E即为旋转中心,E(1,1).
5.[2024·盐城一模]如图,在平面直角坐标系中,点A(3,0),点B(0,4),连接AB,将线段AB绕点A顺时针旋转90°得到线段AC,连接OC,求线段OC的长度.
【解】如图,过点C作CD⊥x轴于点D,则∠ADC=∠BOA=90°.
∵将线段AB绕点A顺时针旋转90°得到线段AC,
∴∠BAC=90°,AC=AB.∴∠BAO+∠CAD=90°.
6. 如图,直线y=2x+2与x轴、y轴分别相交于点A,B,将△AOB绕点A逆时针方向旋转90°得到△ACD,则点D的坐标为________.
(-3,1)
分层练习-巩固
【点拨】当x=0时,y=2×0+2=2,∴点B的坐标为(0,2).∴OB=2.
当y=0时,2x+2=0,解得x=-1,∴点A的坐标为(-1,0).∴OA=1.
根据旋转的性质,可得CD=OB=2,AC=AO=1,AC⊥x轴,CD∥x轴,
∴点D的坐标为(-1-2,1),即(-3,1).
(3,2)
【点拨】如图,连接OA,OA′,过点A作AE⊥x轴于点E,过点A′作A′F⊥x轴于点F,由旋转的性质可知OA=OA′,∠AOA′=90°,∴∠A′OF+∠AOE=90°.
∵AE⊥x轴,A′F⊥x轴,∴∠AEO=∠OFA′=90°.
∴∠OAE+∠AOE=90°.∴∠OAE=∠A′OF.
9.[2024·淮南田家庵区期中]如图,在边长为1的正方形网格中建立平面直角坐标系,△ABC的三个顶点均在格点上.
(1)画出△ABC关于原点对称的△A1B1C1;
【解】如图,△A1B1C1即为所求.
(2)画出△ABC绕点A逆时针旋转90°得到的△AB2C2,并写出点B2,C2的坐标;
【解】如图,△AB2C2即为所求, B2(1,4),C2(-1,5).
(3)若点P为x轴上一点,则PA+PC的最小值为________.
10.在平面直角坐标系中,把一条线段绕其一个端点顺时针旋转,并把这条线段伸长或缩短,称这样的运动为线段的“旋似”,经“旋似”运动后新线段和原线段的夹角称为“旋似角”,新线段长和原线段长的比值称为“旋似比”.如图,在平面直
角坐标系xOy中有一点A(-2,6),
把线段OA绕点O做“旋似”运动,
点A的对应点是点B,若“旋似角”为90°:
分层练习-拓展
(1)当“旋似比”为2时,求点B的坐标;
【解】如图,过点A作AD⊥y轴于点D,过点B作BC⊥x轴于点C,
∴∠ADO=∠BCO=90°.
(2)过点B作BD⊥x轴,点D为垂足,连接AB,若AB∥x轴,求此时的“旋似比”;
【解】如图,设AB与y轴交于点C.
∵A(-2,6),∴AC=2,OC=6.
∵∠AOB=90°,∠COD=90°,
∴∠AOC=∠BOD.
1.给下列图形分类:
(1)只属轴对称;
(2)只属旋转对称;
(3)既属轴对称又属旋转对称;
(4)不属任何对称.
习题24.1
解:(1)只属轴对称:②③⑩.
(2)只属旋转对称:①④⑦.
(3)既属轴对称又属旋转对称:⑤⑨.
(4)不属任何对称:⑥⑧.
2.画出上题中轴对称图形的对称轴,用“”号标出上题中旋转对称图形的旋转中心.
解:图形如图所示.∵AB与A′B′关于点O成中心对称,∴AB=A′B′,AB∥A′B′.
同理得A′B′=A″B″,A′B′∥A″B″.
∴A″B″=AB,A″B″∥AB.
由此得两次中心对称,相当于一次平移.
3.画出已知线段AB关于点O(不在AB上)成中心对称的线段A'B',再画出A'B'关于另一点O'(不与O重合,也不在A'B'上)成中心对称的线段A″B″,并且证明A″B″ AB.由此你能得出怎样的猜想?
4.在方格纸上,格点△ABC的位置如图(1),请在图(2)~(5)中各画出一个与格点△ABC全等但位置不同的格点三角形.
解:如图,三角形即为所求.
5.如图,在平面直角坐标系中有点A(a,b),作出点A关于x轴对称的对应点A1,点A1关于y轴对称的对应点A2.连接OA1和OA2,观察点A1,A2与点O有什么关系?
解:如图所示.点A1,A2与点O的关系是点A1与点A2关于点O成旋转对称.
解:如图.点A,B,C关于原点成中心对称的对应点分别为A′(1,-2),B′(3,-1),C′(2,1).点A关于点B成中心对称的对应点为A″(-5,0).
6.在平面直角坐标系中画出点A(-1,2),B(-3,1),C(-2,-1),并画出这三点关于原点成中心对称的对应点,写出它们的坐标.然后画出点A关于点B成中心对称的对应点并写出其坐标.
7.如图,已知 ABCD的中心在原点O,顶点A(3,2),D(2,-2),求顶点B,C的坐标.
解:∵ ABCD的中心在原点O,
∴点A与C,点B与D分别关于原点对称.
∵A(3,2),D(2,-2),
∴C(-3,-2),B(-2,2).
8.如图,△ABC的顶点坐标分别为A(1,3),B(5,0),C(5,3),将△ABC绕原点O按逆时针方向旋转90°,得△A1B1C1,求顶点A1,B1,C1的坐标.
解:如图所示,△A1B1C1即为所求.顶点A1,B1,C1的坐标分别为(-3,1),(0,5),(-3,5).
9.△ABC在方格纸中的位置如图.
(1)请在方格纸上建立平面直角坐标系,使得
A,B两点的坐标分别为A(2,-1)、B(1,-4),并求出C点的坐标;
解:坐标系如图所示,C(3,-3).
x
y
O
(2)作出△ABC关于x轴对称的△A1B1C1,再作出△ABC以原点为旋转中心、按逆时针方向旋转180°后得到的△A2B2C2,并写出C1,C2两点的坐标;
解:△A1B1C1,△A2B2C2如图所示.其中C1,C2两点的坐标分别为C1(3,3),C2(-3,3).
(3)观察△A1B1C1和△A2B2C2,其中的一个三角形能否由另一个三角形经过某种变换而得到?若能,请指出什么变换.
解:其中的一个三角形能由另一个三角形经过某种变换而得到.是对称变换而得到.
10.在平面直角坐标系中,将抛物线y=4x2绕原点、按逆时针方向旋转180°,求这时抛物线对应的函数表达式.
解:这时抛物线对应的函数表达式为y=-4x2.
旋转的应用
特征
P (x,y)关于原点的对称点为P′(-x,-y).
作图
作出关于原点对称的图形,先求出对称点的坐标,再描点画图.
坐标平面内的旋转
变换
动态图形的操作与图案设计
分析图案设计
分清基本图形
知道形成过程
设计方法
利用图形变换
轴对称
平 移
旋 转
课堂小结
九年级沪科版数学下册 第二十四章 圆
第3课时在平面直角坐标系中对图形进行旋转变换
24.1 旋转
目录/CONTENTS
新知探究
情景导入
学习目标
课堂反馈
分层练习
课堂小结
1. 理解并掌握旋转变化的特点,能够解决坐标平面内的旋转变换问题.(重点、难点)
2. 能够运用旋转、轴对称或平移进行简单的图案设计.(难点)
学习目标
旋转的定义:
在平面内,将一个图形绕着一个定点沿某个方向转动一个角度,得到另一个图形的变换,这样的图形变换称为旋转。
中心对称的定义:
在平面内,将一个图形绕着某一定点旋转180度,得到另一个图形,那么,我们就说这两个图形关于这个点成中心对称。
情景导入
旋转的性质:
1. 旋转不改变图形的大小和形状.
2. 任意一对对应点与旋转中心的连线所成的角相等,都等于旋转角.
3. 对应点到旋转中心的距离相等.
4. 旋转中心是唯一不动的点.
情景导入
中心对称的性质:
关于中心对称的两个图形,对应点所连线段都经过对称中心,并且被对称中心所平分,具有旋转的所有性质.
旋转对称图形:
在平面内,一个图形绕着一个定点旋转一定的角度后,能够与原图_______,这样的图形叫做旋转对称图形,这个定点就是_________.
重合
旋转中心
情景导入
中心对称图形定义:
如果一个图形绕一个点旋转180°后,能和原来的图形互相重合,那么这个图形叫做中心对称图形;这个点叫做它的对称中心.
情景导入
A
B
1
2
2
-1
-2
-2
x
y
O
1
-1
C
如图,△ABC 的顶点坐标分别是 A (2,1),B (0,0).
(1) 分别画出△ABC 以原点为旋转中心,逆时针旋转90°、180°、270°、360°而得到的△A′B′C′,(按逆时针方向旋转)
新知探究
(2)给出点A′,B′,C′的坐标(填在下表中):
A
B
1
2
2
-1
-2
-2
x
y
O
1
-1
C
原图形上点的坐标 A (2,1) B (0,0) C(2,0)
按逆时针方向旋转后对应点的坐标 旋转90°
旋转180°
旋转270°
旋转360°
(-1,2)
(-2,-1)
(1,-2)
(2,1)
(0,0)
(0,2)
(0,0)
(0,0)
(0,0)
(-2,0)
(0,-2)
(2,0)
(3) 分别比较点 A′ 与点 A、点 B′ 与点 B、点 C 与点 C′的坐标,能得到怎样的结论?
通过作图、分析能看到,把一个图形以坐标原点为旋转中心作几个特殊角度的旋转,可得如下结果:
原图形上任一点的坐标 以点O为旋转中心按逆时针方向旋转后对应点坐标
(x,y) (-y,x) (-x,-y) (y,-x) (x,y)
旋转90°
旋转180°
旋转270°
旋转360°
这里,把(x,y)变换成(x,y)的变换叫做恒等变换,即在平面直角坐标系中,一个图形绕点O作360°旋转是一个恒等变换.
x
y
O
1
2
-2
-1
1
2
-2
-1
A
B
C
A′
C′
B′
例1 如图,在平面直角坐标系中,点B的坐标是(1,0),若点 A 的坐标为(a,b),将线段BA绕点B顺时针旋转90°得到线段BA′,则点A′的坐标是 .
(b+1,-a+1)
典例剖析
解析:过点 A 作 AC⊥x 轴,过点 A′ 作 A′D ⊥ x 轴,垂足分别为 C、D,显然
Rt △ABC ≌ Rt △BA′D. ∵点 A 的坐标为 (a,b),点 B 的坐标是 (1,0),∴OD=OB+BD=OB+AC=1+b,A′D=BC=OC-OB=a-1. ∵点 A′ 在第四象限,∴点A′的坐标是(b+1,-a+1).故答案为(b+1,-a+1).
试说出构成下列图形的基本图形.
(1)
(2)
(3)
(4)
新知探究
基本图案
图案的形成过程
分析图案的形成过程
基本图案
图案的形成过程
分析图案的形成过程
归纳:图形的变换可以通过选择不同的变换方式得到,可能需要旋转、轴对称、平移等多种变换组合才能得到完美的图案.
例2 用四块如图(1)所示的正方形卡片拼成一个新的正方形,使拼成的图案是一个轴对称图形,请你在图(2)、图(3)、图(4)中各画出一种拼法(要求三种画法各不相同,且其中至少有一个既是轴对称图形,又是中心对称图形).
解:如图所示.(答案不唯一)
典例剖析
例3 如图,是一个4×4的正方形网格,每个小正方形的边长为1.请你在网格中以左上角的三角形为基本图形,通过平移、轴对称或旋转变换,设计一个精美图案,使其满足:①既是轴对称图形,又是以点O为对称中心的中心对称图形;②所作图案用阴影标识,且阴影部分面积为4.
分析:所给左上角的三角形的面积为 1×1÷2=0.5,故设计图案总共需要三角形 4÷0.5=8 (个).
典例剖析
解:答案不唯一,以下图案供参考.
A
分层练习-基础
2. 如图,点A的坐标是(-4,6),将线段OA绕点O顺时针旋转90°,点A的对应点的坐标是( )
A.(4,6) B.(6,4)
C.(-6,-4) D.(-4,-6)
B
D
4.[2024·德州德城区期末]如图,在正方形网格中,线段AB绕一点旋转一定的角度后与线段CD重合(C,D均为格点,点A的对应点是点C),若点A的坐标为(-1,5),点B的坐标为(3,3),则旋转中心的坐标为________.
(1,1)
【点拨】如图,建立平面直角坐标系,连接AC,BD,作AC,BD的垂直平分线交于点E,点E即为旋转中心,E(1,1).
5.[2024·盐城一模]如图,在平面直角坐标系中,点A(3,0),点B(0,4),连接AB,将线段AB绕点A顺时针旋转90°得到线段AC,连接OC,求线段OC的长度.
【解】如图,过点C作CD⊥x轴于点D,则∠ADC=∠BOA=90°.
∵将线段AB绕点A顺时针旋转90°得到线段AC,
∴∠BAC=90°,AC=AB.∴∠BAO+∠CAD=90°.
6. 如图,直线y=2x+2与x轴、y轴分别相交于点A,B,将△AOB绕点A逆时针方向旋转90°得到△ACD,则点D的坐标为________.
(-3,1)
分层练习-巩固
【点拨】当x=0时,y=2×0+2=2,∴点B的坐标为(0,2).∴OB=2.
当y=0时,2x+2=0,解得x=-1,∴点A的坐标为(-1,0).∴OA=1.
根据旋转的性质,可得CD=OB=2,AC=AO=1,AC⊥x轴,CD∥x轴,
∴点D的坐标为(-1-2,1),即(-3,1).
(3,2)
【点拨】如图,连接OA,OA′,过点A作AE⊥x轴于点E,过点A′作A′F⊥x轴于点F,由旋转的性质可知OA=OA′,∠AOA′=90°,∴∠A′OF+∠AOE=90°.
∵AE⊥x轴,A′F⊥x轴,∴∠AEO=∠OFA′=90°.
∴∠OAE+∠AOE=90°.∴∠OAE=∠A′OF.
9.[2024·淮南田家庵区期中]如图,在边长为1的正方形网格中建立平面直角坐标系,△ABC的三个顶点均在格点上.
(1)画出△ABC关于原点对称的△A1B1C1;
【解】如图,△A1B1C1即为所求.
(2)画出△ABC绕点A逆时针旋转90°得到的△AB2C2,并写出点B2,C2的坐标;
【解】如图,△AB2C2即为所求, B2(1,4),C2(-1,5).
(3)若点P为x轴上一点,则PA+PC的最小值为________.
10.在平面直角坐标系中,把一条线段绕其一个端点顺时针旋转,并把这条线段伸长或缩短,称这样的运动为线段的“旋似”,经“旋似”运动后新线段和原线段的夹角称为“旋似角”,新线段长和原线段长的比值称为“旋似比”.如图,在平面直
角坐标系xOy中有一点A(-2,6),
把线段OA绕点O做“旋似”运动,
点A的对应点是点B,若“旋似角”为90°:
分层练习-拓展
(1)当“旋似比”为2时,求点B的坐标;
【解】如图,过点A作AD⊥y轴于点D,过点B作BC⊥x轴于点C,
∴∠ADO=∠BCO=90°.
(2)过点B作BD⊥x轴,点D为垂足,连接AB,若AB∥x轴,求此时的“旋似比”;
【解】如图,设AB与y轴交于点C.
∵A(-2,6),∴AC=2,OC=6.
∵∠AOB=90°,∠COD=90°,
∴∠AOC=∠BOD.
1.给下列图形分类:
(1)只属轴对称;
(2)只属旋转对称;
(3)既属轴对称又属旋转对称;
(4)不属任何对称.
习题24.1
解:(1)只属轴对称:②③⑩.
(2)只属旋转对称:①④⑦.
(3)既属轴对称又属旋转对称:⑤⑨.
(4)不属任何对称:⑥⑧.
2.画出上题中轴对称图形的对称轴,用“”号标出上题中旋转对称图形的旋转中心.
解:图形如图所示.∵AB与A′B′关于点O成中心对称,∴AB=A′B′,AB∥A′B′.
同理得A′B′=A″B″,A′B′∥A″B″.
∴A″B″=AB,A″B″∥AB.
由此得两次中心对称,相当于一次平移.
3.画出已知线段AB关于点O(不在AB上)成中心对称的线段A'B',再画出A'B'关于另一点O'(不与O重合,也不在A'B'上)成中心对称的线段A″B″,并且证明A″B″ AB.由此你能得出怎样的猜想?
4.在方格纸上,格点△ABC的位置如图(1),请在图(2)~(5)中各画出一个与格点△ABC全等但位置不同的格点三角形.
解:如图,三角形即为所求.
5.如图,在平面直角坐标系中有点A(a,b),作出点A关于x轴对称的对应点A1,点A1关于y轴对称的对应点A2.连接OA1和OA2,观察点A1,A2与点O有什么关系?
解:如图所示.点A1,A2与点O的关系是点A1与点A2关于点O成旋转对称.
解:如图.点A,B,C关于原点成中心对称的对应点分别为A′(1,-2),B′(3,-1),C′(2,1).点A关于点B成中心对称的对应点为A″(-5,0).
6.在平面直角坐标系中画出点A(-1,2),B(-3,1),C(-2,-1),并画出这三点关于原点成中心对称的对应点,写出它们的坐标.然后画出点A关于点B成中心对称的对应点并写出其坐标.
7.如图,已知 ABCD的中心在原点O,顶点A(3,2),D(2,-2),求顶点B,C的坐标.
解:∵ ABCD的中心在原点O,
∴点A与C,点B与D分别关于原点对称.
∵A(3,2),D(2,-2),
∴C(-3,-2),B(-2,2).
8.如图,△ABC的顶点坐标分别为A(1,3),B(5,0),C(5,3),将△ABC绕原点O按逆时针方向旋转90°,得△A1B1C1,求顶点A1,B1,C1的坐标.
解:如图所示,△A1B1C1即为所求.顶点A1,B1,C1的坐标分别为(-3,1),(0,5),(-3,5).
9.△ABC在方格纸中的位置如图.
(1)请在方格纸上建立平面直角坐标系,使得
A,B两点的坐标分别为A(2,-1)、B(1,-4),并求出C点的坐标;
解:坐标系如图所示,C(3,-3).
x
y
O
(2)作出△ABC关于x轴对称的△A1B1C1,再作出△ABC以原点为旋转中心、按逆时针方向旋转180°后得到的△A2B2C2,并写出C1,C2两点的坐标;
解:△A1B1C1,△A2B2C2如图所示.其中C1,C2两点的坐标分别为C1(3,3),C2(-3,3).
(3)观察△A1B1C1和△A2B2C2,其中的一个三角形能否由另一个三角形经过某种变换而得到?若能,请指出什么变换.
解:其中的一个三角形能由另一个三角形经过某种变换而得到.是对称变换而得到.
10.在平面直角坐标系中,将抛物线y=4x2绕原点、按逆时针方向旋转180°,求这时抛物线对应的函数表达式.
解:这时抛物线对应的函数表达式为y=-4x2.
旋转的应用
特征
P (x,y)关于原点的对称点为P′(-x,-y).
作图
作出关于原点对称的图形,先求出对称点的坐标,再描点画图.
坐标平面内的旋转
变换
动态图形的操作与图案设计
分析图案设计
分清基本图形
知道形成过程
设计方法
利用图形变换
轴对称
平 移
旋 转
课堂小结
