29.5 正多边形与圆 课件(共17张PPT)
文档属性
| 名称 | 29.5 正多边形与圆 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-29 07:25:58 | ||
图片预览



文档简介
(共17张PPT)
29.5 正多边形与圆
主讲:
冀教版九年级下册
第29章 直线与圆的位置关系
学习目标
1.了解正多边形和圆的有关概念.
2.理解并掌握正多边形半径、中心角、边心距、边长
之间的关系.
3.会应用正多边形和圆的有关知识解决实际问题.
情境引入
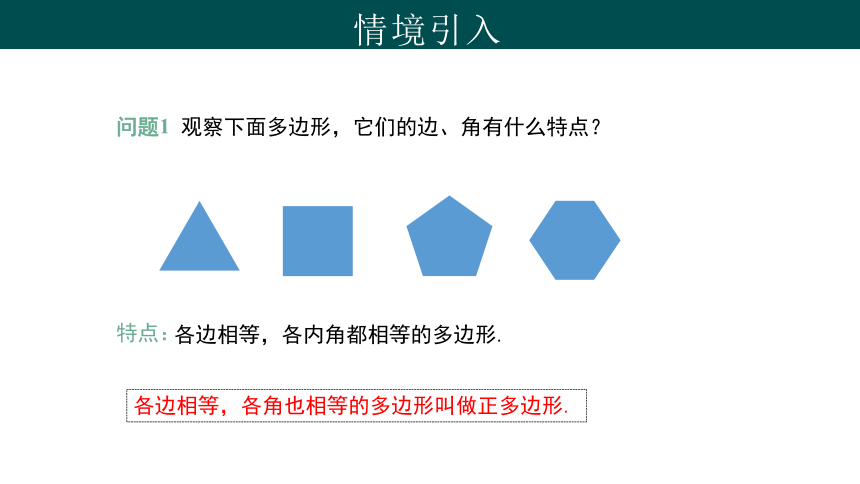
问题1 观察下面多边形,它们的边、角有什么特点?
特点:
各边相等,各内角都相等的多边形.
各边相等,各角也相等的多边形叫做正多边形.
情境引入
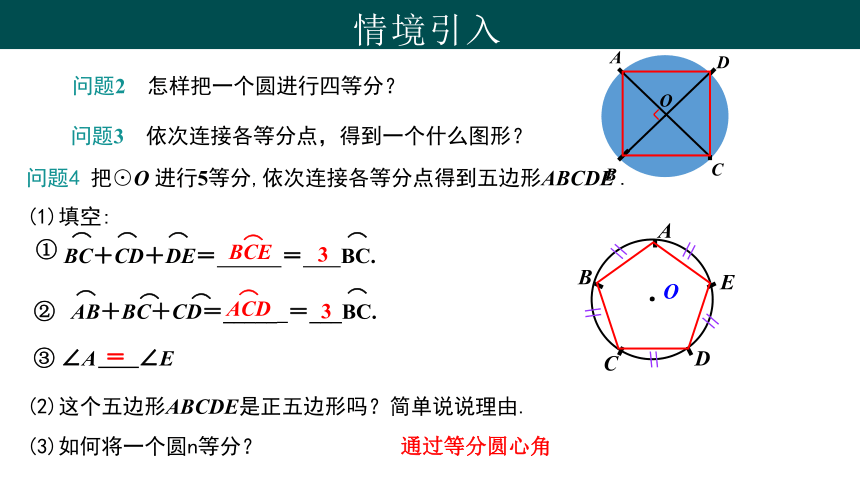
问题2 怎样把一个圆进行四等分?
问题3 依次连接各等分点,得到一个什么图形?
·
A
B
C
D
O
③ ∠A ∠E
问题4 把⊙O 进行5等分,依次连接各等分点得到五边形ABCDE .
(1)填空:
⌒
BCE
⌒
ACD
⌒
AB+BC+CD=_____ =___BC.
⌒
⌒
⌒
②
⌒
BC+CD+DE= = BC.
⌒
⌒
⌒
①
3
3
=
(2)这个五边形ABCDE是正五边形吗?简单说说理由.
·
A
O
E
D
C
B
(3)如何将一个圆n等分?
通过等分圆心角
新知探究
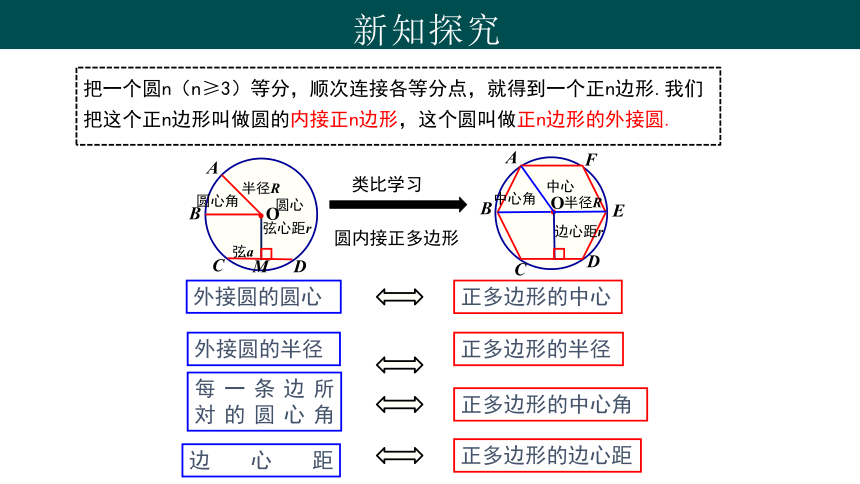
把一个圆n(n≥3)等分,顺次连接各等分点,就得到一个正n边形.我们把这个正n边形叫做圆的内接正n边形,这个圆叫做正n边形的外接圆.
O
C
D
A
B
M
半径R
圆心角
弦心距r
弦a
圆心
中心角
A
B
C
D
E
F
O
半径R
边心距r
中心
类比学习
圆内接正多边形
外接圆的圆心
正多边形的中心
外接圆的半径
正多边形的半径
每一条边所
対的圆心角
正多边形的中心角
边心距
正多边形的边心距
典例精析
用尺规作圆的内接正方形.已知:如图,⊙O.
求作:正方形ABCD内接于⊙O.
例1
作法:
(1)如图,作两条互相垂直的直径AC,BD.
(2)顺次连接 AB,BC,CD,DA.
由作图过程可知,四个中心角都是90°,
所以AB=BC= CD=DA.
因为AC,BD都是直径,
所以∠ABC = ∠BCD= ∠CDA= ∠DAB=90°.
即四边形ABCD为⊙O的内接正方形.
课堂练习
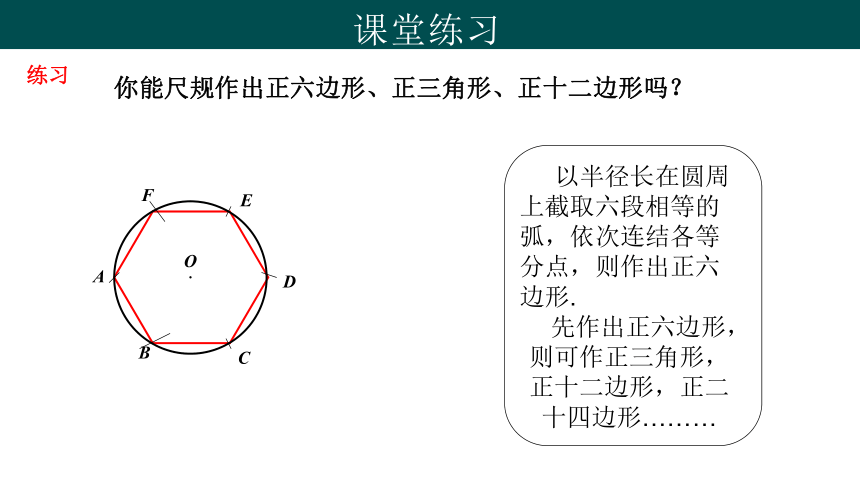
你能尺规作出正六边形、正三角形、正十二边形吗?
O
A
B
C
E
F
·
D
以半径长在圆周上截取六段相等的弧,依次连结各等分点,则作出正六边形.
先作出正六边形,则可作正三角形,正十二边形,正二十四边形………
练习
典例精析
求出半径为r的圆内接正三角形边长和边心距.
解:作等边△ABC的BC边上的高AD,垂足为D
连接OB,则OB=r
在Rt△OBD中 ∠OBD=30°,
边心距=OD=
例2
阶段小结2.作边心距,构造直角三角形.1.连半径,得中心角;OABCDEFRMr·圆内接正多边形的辅助线O边心距r边长一半半径RCM中心角一半方 法 归 纳2.作边心距,构造直角三角形.1.连半径,得中心角;OABC随堂检测
正多边形边数 半径 边长 边心距 周长 面积
3
4 1
6
1. 填表
2
1
2
8
4
2
2
12
2. 若正多边形的边心距与半径的比为1:2,则这个多边形的边数是 .
3
随堂检测
3.有一个亭子它的地基是半径为4m的正六边形,求
地基的周长和面积(精确到0.1平方米).
C
F
A
D
E
.
.
O
B
r
R
P
解:
∴亭子的周长 L=6×4=24(m)
能力提升
1.一个边长为2的正多边形的内角和是其外角和的2倍,则这个正多边形的半径是( )
A.2 B. C.1 D.
A
易错点:误认为正多边形的边心距是正多边形的半径.
3. 要用圆形铁片截出边长为4cm的正方形铁片,则选用的圆形铁片的直径最小要____cm.
也就是要找这个正方形外接圆的直径
2.如图是一枚奥运会纪念币的图案,其形状近似看作为正七边形,则一个内角为 ___度.(不取近似值)
能力提升
A
B
C
D
E
F
P
4.如图,正六边形ABCDEF的边长为 ,点P为六边形内任一点.则点P到各边距离之和是多少?
∴点P到各边距离之和=3BD=3×6=18.
解 : 过P作AB的垂线 , 分别交AB、DE于H、K , 连接BD , 作CG⊥BD于G.
G
H
K
∴P到AF与CD的距离之和 , 及P到EF、BC的距离之和均为HK的长.
∵六边形ABCDEF是正六边形
∴AB∥DE , AF∥CD , BC∥EF ,
∵BC=CD , ∠BCD=∠ABC=∠CDE=120° ,
∴∠CBD=∠BDC=30° , BD∥HK , 且BD=HK.
∵CG⊥BD ,
∴BD=2BG=2×BC×cos∠CBD=6.
课堂小结正多边形正多边形的定义与对称性正多边形的有关概念及性质①正多边形的内角和=②中心角=正多边形的有关计算添加辅助线的方法:连半径,作边心距课后作业
1.如图,AD为⊙O的直径,作⊙O的内接正三角形ABC,甲、乙两人的作法分别如下:
甲:(1)以D为圆心,OD长为半径画圆弧,交⊙O于B,C两点;
(2)连接AB,BC,AC.△ABC即为所求作的三角形.
乙:(1)作OD的中垂线,交⊙O于B,C两点;
(2)连接AB,AC.△ABC即为所求作的三角形.
对于甲、乙两人的作法,可判断( )
A.甲对,乙不对 B.甲不对,乙对
C.两人都对 D.两人都不对
C
课后作业
2.在如图所示的圆中,画出你喜欢的三个不同的圆内接正多边形(画图工具不限,但要保留画图痕迹).
解:
如图所示.
(答案不唯一)
主讲:
感谢聆听
冀教版九年级下册
29.5 正多边形与圆
主讲:
冀教版九年级下册
第29章 直线与圆的位置关系
学习目标
1.了解正多边形和圆的有关概念.
2.理解并掌握正多边形半径、中心角、边心距、边长
之间的关系.
3.会应用正多边形和圆的有关知识解决实际问题.
情境引入
问题1 观察下面多边形,它们的边、角有什么特点?
特点:
各边相等,各内角都相等的多边形.
各边相等,各角也相等的多边形叫做正多边形.
情境引入
问题2 怎样把一个圆进行四等分?
问题3 依次连接各等分点,得到一个什么图形?
·
A
B
C
D
O
③ ∠A ∠E
问题4 把⊙O 进行5等分,依次连接各等分点得到五边形ABCDE .
(1)填空:
⌒
BCE
⌒
ACD
⌒
AB+BC+CD=_____ =___BC.
⌒
⌒
⌒
②
⌒
BC+CD+DE= = BC.
⌒
⌒
⌒
①
3
3
=
(2)这个五边形ABCDE是正五边形吗?简单说说理由.
·
A
O
E
D
C
B
(3)如何将一个圆n等分?
通过等分圆心角
新知探究
把一个圆n(n≥3)等分,顺次连接各等分点,就得到一个正n边形.我们把这个正n边形叫做圆的内接正n边形,这个圆叫做正n边形的外接圆.
O
C
D
A
B
M
半径R
圆心角
弦心距r
弦a
圆心
中心角
A
B
C
D
E
F
O
半径R
边心距r
中心
类比学习
圆内接正多边形
外接圆的圆心
正多边形的中心
外接圆的半径
正多边形的半径
每一条边所
対的圆心角
正多边形的中心角
边心距
正多边形的边心距
典例精析
用尺规作圆的内接正方形.已知:如图,⊙O.
求作:正方形ABCD内接于⊙O.
例1
作法:
(1)如图,作两条互相垂直的直径AC,BD.
(2)顺次连接 AB,BC,CD,DA.
由作图过程可知,四个中心角都是90°,
所以AB=BC= CD=DA.
因为AC,BD都是直径,
所以∠ABC = ∠BCD= ∠CDA= ∠DAB=90°.
即四边形ABCD为⊙O的内接正方形.
课堂练习
你能尺规作出正六边形、正三角形、正十二边形吗?
O
A
B
C
E
F
·
D
以半径长在圆周上截取六段相等的弧,依次连结各等分点,则作出正六边形.
先作出正六边形,则可作正三角形,正十二边形,正二十四边形………
练习
典例精析
求出半径为r的圆内接正三角形边长和边心距.
解:作等边△ABC的BC边上的高AD,垂足为D
连接OB,则OB=r
在Rt△OBD中 ∠OBD=30°,
边心距=OD=
例2
阶段小结2.作边心距,构造直角三角形.1.连半径,得中心角;OABCDEFRMr·圆内接正多边形的辅助线O边心距r边长一半半径RCM中心角一半方 法 归 纳2.作边心距,构造直角三角形.1.连半径,得中心角;OABC随堂检测
正多边形边数 半径 边长 边心距 周长 面积
3
4 1
6
1. 填表
2
1
2
8
4
2
2
12
2. 若正多边形的边心距与半径的比为1:2,则这个多边形的边数是 .
3
随堂检测
3.有一个亭子它的地基是半径为4m的正六边形,求
地基的周长和面积(精确到0.1平方米).
C
F
A
D
E
.
.
O
B
r
R
P
解:
∴亭子的周长 L=6×4=24(m)
能力提升
1.一个边长为2的正多边形的内角和是其外角和的2倍,则这个正多边形的半径是( )
A.2 B. C.1 D.
A
易错点:误认为正多边形的边心距是正多边形的半径.
3. 要用圆形铁片截出边长为4cm的正方形铁片,则选用的圆形铁片的直径最小要____cm.
也就是要找这个正方形外接圆的直径
2.如图是一枚奥运会纪念币的图案,其形状近似看作为正七边形,则一个内角为 ___度.(不取近似值)
能力提升
A
B
C
D
E
F
P
4.如图,正六边形ABCDEF的边长为 ,点P为六边形内任一点.则点P到各边距离之和是多少?
∴点P到各边距离之和=3BD=3×6=18.
解 : 过P作AB的垂线 , 分别交AB、DE于H、K , 连接BD , 作CG⊥BD于G.
G
H
K
∴P到AF与CD的距离之和 , 及P到EF、BC的距离之和均为HK的长.
∵六边形ABCDEF是正六边形
∴AB∥DE , AF∥CD , BC∥EF ,
∵BC=CD , ∠BCD=∠ABC=∠CDE=120° ,
∴∠CBD=∠BDC=30° , BD∥HK , 且BD=HK.
∵CG⊥BD ,
∴BD=2BG=2×BC×cos∠CBD=6.
课堂小结正多边形正多边形的定义与对称性正多边形的有关概念及性质①正多边形的内角和=②中心角=正多边形的有关计算添加辅助线的方法:连半径,作边心距课后作业
1.如图,AD为⊙O的直径,作⊙O的内接正三角形ABC,甲、乙两人的作法分别如下:
甲:(1)以D为圆心,OD长为半径画圆弧,交⊙O于B,C两点;
(2)连接AB,BC,AC.△ABC即为所求作的三角形.
乙:(1)作OD的中垂线,交⊙O于B,C两点;
(2)连接AB,AC.△ABC即为所求作的三角形.
对于甲、乙两人的作法,可判断( )
A.甲对,乙不对 B.甲不对,乙对
C.两人都对 D.两人都不对
C
课后作业
2.在如图所示的圆中,画出你喜欢的三个不同的圆内接正多边形(画图工具不限,但要保留画图痕迹).
解:
如图所示.
(答案不唯一)
主讲:
感谢聆听
冀教版九年级下册
